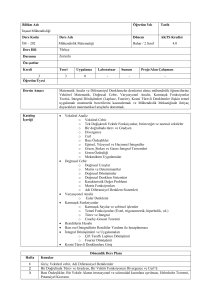
TC
SAKARYA ÜNİVERSİTESİ
TEKNOLOJİ FAKÜLTESİ
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ
ELM202
ELEKTRONİK-II DERSİ
LABORATUAR FÖYÜ
DENEYİ YAPTIRAN:
DENEYİN ADI:
DENEY NO:
DENEYİ YAPANIN
ADI ve SOYADI:
SINIFI:
OKUL NO:
DENEY GRUP NO:
DENEY TARİHİ
RAPOR TESLİM TARİHİ
KONTROL
DEĞERLENDİRME
Ön Çalışma
(%20)
Deney
Sonuçları
(%20)
Deney No:
19
Sözlü
(%20)
Deney
Performansı
(%20)
Deney
Raporu
(%20)
Program Çıktıları
1, 2, 3, 4, 5
TOPLAM
Elektronik Dersi Deney Föyleri
DENEY 19:
Doc.Dr. Ali Fuat Boz
OP-AMPLARIN DİFERANSİYEL VE İNTEGRAL ALICI OLARAK KULLANIMI
TANITIM ve AMAÇ:
Op-amplara işlemsel yükselteç(operational amplifier) denmesinin asıl sebebi, bu devre elemanlarının gerçekte
matematiksel işlemler için kullanılmalarıdır. Örneğin toplama, çıkarma, diferansiyel ve integral alma gibi.
Yüksek hızlı dijital bilgisayarların yaygınlaşmasından önce op-amplar analog bilgisayar uygulamalarında çok sık
kullanılmışlardır. Bu uygulama bugün için görsel olarak kaybolmasına rağmen, burada kullanılan devreler bugün
dahi çok fazla kullanım alanına sahiptir.
Bu deney bir önceki op-amp tanıtım deneyinin geliştirilmesinden ibarettir. Temelde aynı
devre kullanılmasının yanısıra, devrede yapılan bir iki küçük değişiklik ile devrenin
fonksiyonu bir önceki uygulamadan oldukça farklılaştırılmıştır. Önceki deney gibi, bu
deneydede yapılan ölçmeler kaydedilecek ve osilaskopta görülen dalga şekilleri çizilecektir.
Bu işlemlerden sonra rapor tartışma ve sonuç bölümleri ile bitirilecektir.
DEVRELER:
1- Diferansiyel (Türev) Alıcı devre:
Şekil-1’de basit bir diferansiyel alıcı devre şeması verilmiştir. Bu devre şekilden de görüldüğü
gibi 1. deneyde yapılan eviren yükselteç devresi ile benzerlikler taşımaktadır. Arasındaki fark
1. deneyde kullanılan R1 direnci burada C1 kondansatörü ile değiştirilmiştir. Devrenin çıkış
voltajını veren formül aşağıda verilmiştir.
dvi
(1)
Vo C1R2
dt
burada vi giriş voltajıdır.
dvi
Bu sonuç teorik olarakta gördüğümüz kondansatör üzerinden geçen ve i C1
ile
dt
belirlenen akım değerinin bir sonucudur ve çıkış voltajı oransal olarak giriş sinyalindeki
değişim oranına bağlıdır.
R2
C1
IC1
IP
741
Şekil-1
OP
İdeal Diferansiyel Alıcı Devre
Yaklaşık Diferansiyel Alıcı:
Pratikte Şekil-1’de verilen basit devre yetersiz kalmaktadır. Bunun nedeni çıkış voltajının
verilen denklemden de görülebileceği gibi, sabit bir giriş gerilimi için sıfır olmasıdır. Asıl
problem giriş sinyalindeki ani değişimler ile ortaya çıkmaktadır. Formül 1’dende
görülebileceği gibi giriş sinyali çok küçük olsa dahi eğer giriş sinyalindeki hızlı değişim oranı
çok büyük ise, çıkış voltajıda büyük olacaktır. Tahmin edilebileceği gibi pratikte sinyallerin
büyük bir bölümü aynı zamanda istenmeyen gürültüler(noise)’de içermektedir. Bu gürültüler
düzenli olabileceği gibi rasgelede değişebilmektedir. Buradan, eğer giriş sinyalindeki gürültü
2
Elektronik Dersi Deney Föyleri
Doc.Dr. Ali Fuat Boz
bileşeni çok hızlı bir şekilde değişirse Şekil-1’deki devre çok büyük bir çıkış sinyali
verecektir. Bunun anlamı devremiz girişteki gürültü bileşenini yükseltmektedir, bu ise
istenmeyen bir durumdur.
Bu problemi çözmek için Şekil-2’dende görüldüğü gibi R1 direnci C1 kondansatörüne seri
olarak bağlanmıştır. Bu, devrenin kazancını yüksek frekans değerlerinde -R2/R1 oranı ile
kısıtlayacak ve böylece yüksek frekanslı gürültü bileşenleri yükseltme işlemine tabi
tutulmayacaklardır. Bu devrenin dezavantajı ise, devrenin yalnızca eğer giriş sinyalindeki
değişim yavaş ise yani frekans düşük ise diferansiyel alıcı olarak çalışmasıdır. Bu yüzden bu
devreye yaklaşık diferansiyel alıcı devresi denmektedir.
Buradan anlaşıldığı gibi devre iki çalışma bölgesine sahiptir, yani I. Bölgede devre
diferansiyel alıcı, II. Bölgede ise kazancı sabit bir yükselteç olarak çalışmaktadır. Bu iki
bölgeyi ayıran ise kritik frekans f c değeridir. f c frekansından küçük frekans değerlerinde
devre diferansiyel alıcı olarak, f c frekansından büyük frekans değerlerinde ise kazancı
–R2/R1 değerinde sabit bir yükselteç devresi olarak çalışmaktadır.
f c kritik frekansının değeri
1
(Hz)
(2)
fc
2C1R1
formülünden bulunabilir. Burada C1 farad ve R1 ohm değerinde olacaktır.
R2
100K
C1
IP
R1
IC1
10K
15n
OP
741
R3
100K
GND
Şekil-2
GND
Yaklaşık Diferansiyel Alıcı Devre
2- İntegral Alıcı (İntegratör):
Tam İntegral Alıcı:
Şekil-3’de tam integral alıcı devresinin şeması verilmiştir. Devre eviren yükselteç ile
benzerlikler taşımaktadır, arasındaki fark eviren yükselteç devresindeki R2 direnci burada C2
kondansatörü ile değiştirilmiştir. Devrenin çıkış voltajı
1
Vo
vi dt
(3)
C2 R1
formülünden bulunabilir.
C2
R1
IC1
IP
741
OP
GND
Şekil-3 İdeal(tam) İntegral Alıcı Devre
3
Elektronik Dersi Deney Föyleri
Doc.Dr. Ali Fuat Boz
İdeal diferansiyel alıcı gibi bu devreninde pratikte kullanımı çok zordur, çünkü çıkış zaman ile sürüleceği için,
çıkış voltajı op-amp doyuma gidinceye kadar artacak bundan sonrada devrenin aktif olarak çalışması duracaktır.
Bu durumun daha iyi anlaşılması için örneğin vi giriş voltajının sabit bir değerde olduğunu farz edelim. Bu
durumda yukarıda verilen çıkış voltajı formülünden çıkış voltajı hesaplanır ise sonucun
1
(4)
vit c
C2 R1
olduğu görülecektir. Burada c integral sabitidir ve devrenin çıkış voltajının t=0 olduğu andaki
değerine eşittir. Bu formülden görüldüğü gibi çıkış voltajı zaman ile artacaktır. Teorik olarak
bu artış sonsuza dek devam edecek, pratikte ise bu artış devre doyuma ulaşıncaya kadar yani
çıkış voltajı yaklaşık besleme kaynağının voltajına ulaşıncaya kadar devam edecek ve bundan
sonrada bu değerde sabit kalacaktır. Bu durum giriş voltajının çok küçük olduğu durumlarda
dahi görülecektir, yalnızca bu durumda çıkış voltajının doyum gerilimine ulaşması biraz daha
uzun bir süre alacaktır. Hatta giriş voltajı vi ‘nin sıfır olduğu durumda dahi, op-amp
içerisindeki transistörlerin karakteristik uyumsuzluklarından dolayı bir giriş offset voltajı
oluşacağından, bu voltaj sanki op-amp’ın girişinde küçük bir vi giriş sinyali varmış gibi
davranacak ve devre doyum değerine ulaşıncaya dek zamanla çıkış voltajını arttıracaktır. Bu
şartlar altında eğer pratikte bir tam integral alıcı devresine ihtiyaç duyulursa, örneğin kontrol
ve ölçü aletleri devreleri gibi, karakteristik özellikleri 741 op-ampından daha iyi bir op-amp
seçilmeli ve buna ilaveten devreye offset sıfırlama(offset-null) devreside ilave edilmelidir.
Böylece devre tam integral alıcı olarak çalıştırılabilir.
Vo
Yaklaşık İntegral Alıcı Devresi:
Bir çok uygulama için tam integral alıcının zamanla sürülmesi problemi C2 kondansatörüne
paralel bir R2 direnci bağlamakla çözülebilmektedir. Bu durumda eğer giriş gerilimi sabit
tutulsa devre kazancı -R2/R1 olan bir yükselteç olarak çalışacaktır. Devrenin integratör
olarak çalışması ise, eğer giriş gerilimi oldukça hızlı şekilde değişirse, yani frekans yüksek ise
mümkün olacaktır. Bu yüzden bu devreye yaklaşık integral alıcı denmektedir.
Diferansiyel alıcı devrede olduğu gibi, bu devre içinde iki çalışma bölgesini ayıran bir kritik
frekans, f c , değeri vardır. Bu değerden büyük frekans değerleri için devre integratör olarak
çalışırken, küçük değerleri için kazancı –R2/R1 olan bir yükselteç olarak çalışacaktır.
f c frekans değeri bu devre için
fc
1
2C2 R2
(Hz)
(5)
formülünden bulunabilir.
R2
C2
100K
15n
R1
IP
IC1
10K
741
R3
OP
10K
GND
Şekil-4 Yaklaşık İntegratör Devresi
4
Elektronik Dersi Deney Föyleri
Doc.Dr. Ali Fuat Boz
3-Devrenin Montajı:
Deney yapacak her gruba
1 adet 741 op-amp entegresi
1 adet 15 nF kondansatör
2 adet 100 nF kondansatör
2 adet 10 K direnç
2 adet 100 K direnç verilecektir.
Deney sonunda malzemeler malzeme odasındaki kutulara değerlerine göre tekrar
yerleştirilecektir.
Sırası ile Şekil-2 ve Şekil-4’ teki devreler bread board üzerine kurulacaktır. Devrenin montajı
bittiğinde açık şema üzerinde gösterilmeyen 100 nF’lık kondansatörler simetrik besleme
kaynağının +Vcc ile -Vee uçları ile şase (GND) arasına bağlanacaktır. Bu kondansatörlerin
görevi güç kaynağından gelebilecek parazitleri şaseye aktararak, devrenin performansını
korumaktır. Bu kondansatörlere güç kaynağı dekuplaj kondansatörleride denmektedir.
Besleme kaynağı olarak 12V simetrik güç kaynağı kullanılacaktır. 741 entegresinin ayak
bağlantıları deney yapraklarının sonunda verilecektir.
4-Test İşlemleri:
Yaklaşık Diferansiyel alıcı:
1- osilaskobun I. Kanalını diferansiyel alıcı devrenin girişine, II. Kanalınıda çıkışına
bağlayınız. Osilaskobun II. Kanalını terslemek için INV tuşuna basınız.
2- Yine sinyal jeneratörünü devre girişlerine bağlayarak, çıkışını 33 Hz üçgen dalga şekline
ayarlayınız.
3-
Sinyal jeneratörünün çıkış voltajını osilaskop ile ölçerek 1 Vp-p değerine ayarlayınız. Bu
durumda devrenin çıkışında üst ve alt kısımları, giriş üçgen dalgasının yükselen ve düşen
kenarları ile çakışan(eşzamanlı) bir kare dalga görmeniz gerekir. Bulduğunuz bu dalga
şekli bir diferansiyel alıcı devresinden beklediğiniz bir sonuçmudur? Eğer bu sizin için bir
sürpriz oldu ise, üçgen dalganın önce pozitif sonra negatif olan ve eğimi sabit olan kenarlarını
gözlemleyiniz, gözlem sonucunu raporda belirtiniz.
4- Teorik olarak diferansiyel alıcı devresi çıkış voltajının tepeden tepeye(peak to peak)
değerini üçgen giriş dalgasının kenar eğimlerinden çıkarabiliriz. Sonuç V0 (4 fR2C1 )Vi
formülü ile bulunabilir. Burada f Hertz olarak frekansı, Vi de giriş voltajının tepeden
tepeye olan değerini ifade eder. Şimdi bu formül yardımı ile bulduğunuz sonucu devreden
ölçüm yoluyla elde ettiğiniz sonuçla karşılaştırınız. Pratik olarak ölçülen değer ile teorik
olarak hesaplanan değer arasında önemli bir fark varmı? Varsa nedenleri ne olabilir ?
Ayrıca böyle bir fark sizce bu devre için normalmidir?
5- Şimdi sinyal jeneratörünün frekansını 33 Hz’in üzerine yavaş yavaş çıkarın ve çıkış
voltajındaki değişimi genlik ve dalga şekli olarak gözlemleyiniz. Çıkış dalga şeklini
ölçekli olarak değişik frekanslar için milimetrik kağıda çiziniz. Yine devrenin diferansiyel
alıcı olarak çalıştığı en yüksek frekansı çıkış dalga şeklini gözlemleyerek not ediniz.
Şimdi bu değeri çizeceğiniz kazanç-frekans grafiği üzerinde işaretleyiniz. Bu frekans
değeri daha önceden hesapladığınız kritik frekans değeri ile uyuşuyormu? Frekanslar
farklı ise sebebi ne olabilir? Kısaca tartışınız.
5
Elektronik Dersi Deney Föyleri
Doc.Dr. Ali Fuat Boz
Sinüs Dalga Testi:
Bu bölümde diferansiyel alıcı devrenin sinüs giriş sinyaline gösterdiği tepki incelenecektir.
Deneydende görüleceği üzere diferansiyel alıcı devre sinüs giriş sinyaline daha önce yapılan
eviren yükselteç devresinden çok farklı bir tepki gösterecektir. Bu tepki sonucu kazanç sabit
kalmayacak ve frekansla değişecektir.
1- Sinyal jeneratörünü diferansiyel devre girişine bağladıktan sonra frekansı 10 KHz’e
ayarlayınız.
2- Giriş sinyalinin genliğini sinyal jeneratöründen 1 Vp-p olacak şekilde ayarlayınız.
3- Osilaskobun II. Kanalını devre çıkışına bağlayarak bu çıkışı osilaskop düğmelerini
kullanarak tersleyiniz(tersleme işlemini o kanala ait fonksiyon düğmelerinden INV yazanı
sağlayacaktır).
4- Bu durumda çıkış sinyali ile giriş sinyali yaklaşık aynı fazlı olmalıdır.
5- Şimdi çıkış voltajını, V0 , osilaskop üzerinden ölçünüz ve devrenin kazancını V0 / Vi
formülünden hesaplayınız. Bu değeri R2 / R1 değeri ile karşılaştırınız, bu iki değerin
yaklaşık aynı olduğu görülecektir.
6- Şimdi giriş sinyalinin frekansını 4.6 KHz’e genliğinide 1 Vp-p değerine ayarlayınız. Bu
durumda çıkış voltajını ölçünüz ve V0 / Vi formülünden kazancı bulunuz.
7- Bu son işlemi 2.2KHz, 1 KHz, 460 Hz, 220 Hz ve 100 Hz için tekrarlayarak giriş ile çıkış
arasındaki faz kaymasına dikkat ediniz.
8- Devrenin kazanç-frekans grafiğini çizmek için bu yedi frekans değerini x koordinat
düzleminde aralarında eşit mesafe bırakarak işaretleyiniz. Bu işaretleme ile logaritmik
frekans ölçeği elde edilecek ve bu şekilde devrenin davranışı doğrusal (lineer) frekans
ölçeğinden daha iyi bir şekilde görülebilecektir. Her frekans değerine karşılık gelen
kazanç değerlerini(önceki basamaklarda V0 / Vi formülünden bulduğunuz) y koordinatına
işaretleyerek devrenin kazanç-frekans grafiğini tamamlayınız.
9- Şimdi bu grafik üzerinde daha önce formül-2’den hesapladığınız
işaretleyiniz.
f c frekansını
İntegral Devresi:
Kare Dalga Testi:
1- Şekil-4’teki integral devresini kurunuz.
2- Sinyal jeneratörünü devre girişine bağlayarak 3.3 KHz, 1 Vp-p değerinde kare dalgaya
ayarlayınız.
6
Elektronik Dersi Deney Föyleri
Doc.Dr. Ali Fuat Boz
3- Osilaskobun I. Kanalını devre girişine, II. Kanalını devre çıkışına bağlayınız, ve II. Kanalı
terleyiniz(INV tuşuna bas)
4- Devre çıkışında yükselen ve düşen kenarları kare dalganın üst ve alt kısımları ile çakışan
bir üçgen dalga görmeniz gerekmektedir.
5- Çıkışta gördüğünüz bu dalga şekli sizin bir integratör devresinden beklediğiniz bir
sonuçmudur? Bu sonucu doğrulamak için 4 nolu formülü, giriş kare dalga sinyalinin her
ayrım periyodu için ayrı ayrı uygulayınız ve sonuçları raporda belirtiniz
6- İntegral devresi çıkış voltajının tepeden tepeye değeri giriş sinyalinden bulunabilir. Bunun
Vi
için
formülünü kullanınız. Şimdi çıkış voltajını devreden ölçüm yolu
V0
4 fR1C2
ile bularak bu formülden bulduğunuz snuç ile karşılaştırınız.
7- Giriş sinyalinin frekansını 3.3 KHz’den aşağıya dogru kademeli olarak azaltınız, her
kademede çıkış voltajını gözlemleyerek voltaj değerlerini kaydediniz ve dalga şeklndeki
değişikliklere dikkat çekiniz. Devrenin integratör olarak çalıştığı frekans değerini bularak
not ediniz. Şimdi kaydettiğiniz kazanç ve frekans değerlerini kullanarak bir grafik çiziniz
ve grafik üzerinde daha önce kaydettiğiniz ve devrenin iyi bir integratör olarak çalıştığı en
düşük frekans değerini işaretleyiniz.
Sinüs Dalga Testi:
1- Şimdi devre girişine tepeden tepeye genliği 1 V ve frekansı 10 Hz olan bir sinüs dalgası
uygulayınız.
2- Aynı anda osilaskobun II kanalınıda çıkışa bağlayarak her iki sinyalin yaklaşık aynı fazlı
olduğunu görünüz.
3- Devrenin çıkış voltajını ölçerek kaydediniz ve V0 / Vi formülünden devrenin kazancını
hesaplayınız. Bulduğunuz bu değer ile R2 / R1 değerini karşılaştırınız, here iki değerin
yaklaşık aynı olması gerekmektedir, eğer farklılık var ise devrenizi ve ölçümlerinizi
kontrol ediniz.
4- Giriş sinyalinin frekansını 22 Hz’e yükseltiniz bu durumda giriş sinyalinin genliği 1 Vp-p
olmalıdır. Şimdi çıkış voltajını ölçerek, devrenin kazancını V0 / Vi formülünden
hesaplayınız.
5- Bu son işlemleri 46 Hz, 100 Hz, 220 Hz, 460 Hz ve 1000 Hz için tekrarlayınız ve
sonuçları kaydediniz. Frekans değeri yükseldikçe giriş sinyali ile çıkış sinyali arasında
oluşan faz kaymasına dikkat çekiniz.
6- Diferansiyel alıcı devrede olduğu gibi bu devrenin kazanç-frekans grafiğini çizmek için
yyukarıdaki yedi frekans değerini aralarında eşit mesafe olacak şekilde X koordinat
düzlemine işaretleyiniz, böylece logaritmik frekans düzlemi elde etmiş ve lineer
düzlemden daha fazla bir frekans aralığını aynı anda görme imkanını sağlamış oluyoruz.
7
Elektronik Dersi Deney Föyleri
Doc.Dr. Ali Fuat Boz
Burada bulunan yedi frekans değeri için daha önceden hesapladığınız kazanç değerlerini
Y düzlemine işaretleyerek devrenin kazanç-frekans grafiğini tamamlayınız.
7- Çizdiğiniz bu grafik üzerinde 5 nolu formülden bulduğunuz kritik frekans değerini
işaretleyiniz. Tartışma ve sonuç bölümlerinde bu frekans değerinden büyük ve küçük
frekans değerleri için devrenin davranışını yazınız. Bu sonuçları teorik olarak olması
gereken değerlerle karşılaştırınız ve eğer aralarında fark var ise sebepleri hakkında fikir
yürüterek raporda yazınız.
8