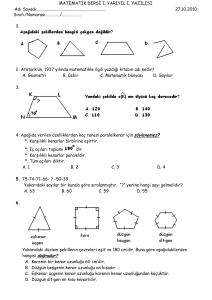
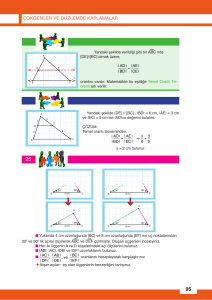
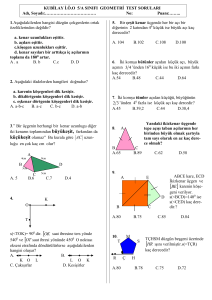
BHL206 MATEMATİK

BERK HAZIRLIK LİSESİ DERS REHBERLERİ
2015-2016 EĞİTİM YILI
BHL206
MATEMATİK
BHL-206 Matematik
Berk Hazırlık Lisesi’ne Hoş geldiniz...
İnsanlık tarihi boyunca ihtiyaçlar ekseninde mükemmeli aramak bizlerin en temel dürtülerinden birisi olmuştur. Küreselleşen
dünyamızda ön plana çıkan en önemli ihtiyaçlarımızdan birisi de eğitimdir. Öyle ki günümüzde eğitim, bireylerin gelecekte
oluşacak maddi ve manevi ihtiyaçlarını karşılayabilecek donanımda olabilmelerini sağlamak için yapılması gereken en kalıcı
yatırımlardan biri haline gelmiştir.
Eğitim-öğretim faaliyetlerinde yönetici, öğretmen, öğrenci, veli ve personel olarak insan unsuru ön plana çıkmaktadır. Eğitim
sürecinde farklı rollere sahip bu unsurların uyum içerisinde bir arada olabilmesinin en önemli koşullarından birisi de ortak bir
hedef doğrultusunda hareket edilebilmesidir. Bu anlamda Berk Hazırlık Lisesinin hedefi toplumun her kesiminin iştirak
edebileceği ayrıcalıklı bir eğitim sistemini en uygun şartlarda sunarak geleceğin bir kader değil çocuklarımızın değiştireceği bir
zaman dilimi olmasını sağlamaktır. Bu hedef doğrultusunda kısa zamanda tüm Türkiye de açacağımız okullarla toplumun tüm
kesimlerinin faydalanabileceği ayrıcalıklı bir eğitim sürecinden yetişen dışa dönük ve mükemmeliyetçi nesiller başarımızın en
büyük nişanı olacaktır.
Arzuladığımız ayrıcalıklı eğitimi sunma sürecinde ortaya çıkabilecek sorunları erkenden tespit ederek önleyecek yöneticiler,
süreci etkin bir rehberlik sistemi ile kontrol altında tutacak eğitmenler ve sistemin işleyişinde öneri ve geri bildirim yoluyla
değişimin ve gelişimin habercisi olacak öğrenciler ve veliler belirlediğimiz idari birimler ile sürekli bir koordinasyon halinde
olmalıdır. Çünkü böylesi bir koordinasyon ile okul kaynak ve imkânlarının da hedefe odaklı ve verimli kullanılması
sağlanacaktır.
İnanıyoruz ki, Berk Hazırlık Lisesi eğitimcileriyle, öğrencileriyle, velileriyle ve personeliyle büyük bir ailedir. Bu ailenin özverili
çalışmaları, birliği ve beraberliği mükemmeli arayan ayrıcalıklı bir nesile köprü olacaktır.
Bu vesile ile beraber yola çıktığımız Berk Hazırlık Lisesi ailesinin tüm bireylerine şükranlarımızı sunar, özellikle değerli
velilerimize ilgi ve destekleri için teşekkür eder, tüm öğrencilerimize sağlıklı, başarılı ve mutlu bir eğitim yılı dileriz.
“Üniversiteye Hazırlar, Geleceğinizi Planlar ”
BHL-206 Matematik
BERK HAZIRLIK LİSESİ
BHL-206 MATEMATİK
Ders Rehberi
2015-2016
Sevgili öğrenciler;
Başarılı bir lise öğreniminin devamı olan 10. sınıftaki performansınızla doğrudan ilgilidir. Yeni bilgiler, fırsatlar
ve araçlar matematiğe bakış açımızı, matematikten beklentilerimizi, matematiği kullanma biçimimizi ve hepsinden
önemlisi matematik öğrenme ve öğretme süreçlerimizi yeniden şekillendirmektedir.
Teknolojik gelişmelerle birlikte daha önceki kuşakların karşılaşmadığı yeni problemlerle karşılaşılan günümüz
dünyasında, matematiğe değer veren, matematiksel düşünme gücü gelişmiş, matematiği modelleme ve problem
çözmede kullanabilen bireylere her zamankinden daha çok ihtiyaç duyulmaktadır.
Matematik tarihi pek çok önemli ve bir o kadar da ilginç kişi ve anekdotlarla doludur. Bu tarihsel kişilikler,
onların hayatları, eserleri ve matematiğe yaptıkları katkılar hakkında bilgiler paylaşmak matematik derslerini öğrenciler
için daha anlamlı kılacaktır. Örneğin Antik Yunan’ın en önemli geometricilerinden Öklit’in hayatını ve en önemli eseri
“Elementler”i tanıma fırsatı bulan öğrenciler bugün öğrendikleri geometri konularının bundan en az 2500 yıl önce ortaya
konduğunu ve bu bilgilerin bir tarihi miras olarak kültürden kültüre aktarıldığını göreceklerdir. İnsanlık tarihine katkıda
bulunmuş daha pek çok matematikçi vardır.
Bu kapsamda matematik dersi ile öğrencilerin;
• Problem çözme becerilerini geliştirmeleri,
• Matematiksel düşünme becerisi kazanmaları,
• Matematiğin kendine has dilini ve terminolojisini doğru ve etkili bir şekilde kullanabilmeleri,
• Matematiğe ve matematik öğrenimine değer vermelerinin sağlanması amaçlanmıştır.
Ders Öğretmeni: Zülfiye Sevinç ÖZEL
Okul Telefon: 0212 690 92 07
Okul Email : info@meslegimokullari.com
Web adresi: www.meslegimokullari.com
Facebook: www.facebook.com/meslegimokullari
BHL-206 Matematik
Amaç ve Hedefler
Matematik programımızla hedeflediğimiz matematiksel beceri ve yeterlilikler şunlardır:
I. Matematiksel modelleme ve problem çözme:
Matematiksel modelleme bir yandan öğrencilerin matematiksel düşünme becerilerini geliştirirken diğer yandan
matematiğin gerçek hayattaki rolünü görmelerini ve matematiğe değer vermelerini sağlar.
II. Matematiksel süreç becerileri: Matematiksel dili ve terminolojiyi doğru ve etkin kullanma:
Matematik hakkında konuşma, yazma ve dinleme iletişim becerilerini geliştirirken aynı zamanda öğrencilerin
matematiksel kavramları daha iyi anlamalarına da yardımcı olur. Öğretmen, öğrencilerin düşüncelerini açıklayabilecekleri,
tartışabilecekleri ve yazılı olarak ifade edebilecekleri sınıf ortamları oluşturulacak ve öğrencilerin daha iyi iletişim
kurabilmesi için uygun sorgulamalarda bulunulacaktır.
III. Matematiğe ve öğrenimine değer verme: Bu çerçevede öğrencilerin matematikle ilgili duyuşsal gelişimleri, tutumları, öz
güvenleri ve kaygıları dikkate alınacaktır. Bunun için öğrenme – öğretme sürecinde matematiğin bugünkü medeniyetimizin
gelişmesindeki, diğer disiplinlerdeki ve günlük hayatımızdaki rolünü ortaya koyan etkinliklere yer verilecektir.
IV. Psikomotor becerilerde gelişim sağlama:
Öğrencilere aşağıdaki psikomotor becerilerin kazandırılması hedeflenmiştir:
• Grafikleri aslına uygun bir şekilde çizme
• Geometrik araç-gereçleri (pergel, cetvel, vb.) temel geometrik çizimlerde kullanma
• Bilgi ve iletişim teknolojilerini kullanma
V. Bilgi ve İletişim Teknolojilerini yerinde ve etkin kullanma:
Günümüzde bilgi ve iletişim teknolojileri büyük bir hızla gelişmekte ve anlamlı matematik öğretimi için yeni
fırsatlar oluşturmaktadır. Bilgisayar teknolojisinin sürekli gelişmesi sonucunda; öğretim yazılımlarının hem niteliği hem de
niceliği artmakta, alternatifler sürekli çoğalmaktadır. Bilgi ve iletişim teknolojilerinin bilinçli kullanımı, teknolojinin
matematik becerilerinin öğrenilmesinin yerini almasını değil; aksine, beceri seviyelerini gözetmeksizin tüm öğrencilere
matematiksel düşünceyi ulaşılabilir kılmayı amaçlamaktadır.
Eğitim / Öğretim Metodolojisi
2015-2016 eğitim öğretim yılı süresince matematik dersleri haftalık 6 ders saati şeklinde olacaktır. Matematik
dersinden 2 yazılı sınav yapılacaktır, ayrıca 2 performans ve 1 proje değerlendirilmesi de yapılacaktır.
Yazılı sınav formatı çoktan seçmeli, boşluk doldurmalı, doğru-yanlış ve klasik soru tiplerinden oluşur.
Matematik dersinde uygulanan eğitim/öğretim metotları aşağıdaki gibidir;






Anlatma Metodu: Matematik dersinde en çok kullanılan metotlardan biridir. Öğretmen merkezli bir yöntemdir.
Öğretmenin herhangi bir konuyu, karşısında oturan öğrencilere iletmesi biçiminde uygulanmaktadır.
Soru-Cevap Metodu: Sık kullanılan metotlardan biridir. Öğrenci merkezli bir yöntemdir. Öğrencilerin derse ve
konuya karşı ilgi ve dikkatlerini artırır, onların derse istekle katılmalarını sağlar.
Tartışma: Herhangi bir grubun veya bir başkanın yönetimi altında, belirli bir düzen içinde belli bir amaca dönük
karşılıklı münazaralardır. Tartışma metodunda hem öğretmenle öğrenci arasında hem de öğrenciler arasında
dinamik bir etkileşim, alış–veriş hedeflenir. Tartışma metodu, öğrencilerin ilgisini uyandırır, anlayışlarını
değerlendirme, gerçekleri kavrama, eleştirici düşünme kabiliyetlerini geliştirir.
Problem Çözme Metodu: Öğrencilerde kalıcı öğrenmeyi sağlar. Bu metotla öğrenci problem çözdükçe kendine
olan güveni artar.
Grupla Çalışma Metodu: Konuya göre kullanılan bir metotdur. Grupla çalışma, öğrencinin sosyal gelişimine de
katkı sağlayan bir metottur. Bu metot öğrencilerden oluşturulan gruplara birer konu verilmesi ve konunun
öğrencilerce araştırılarak, sınıfta grup halinde anlatılması şeklinde olmaktadır.
Araştırma: Öğrencide merak uyandırır ve verilen bir konu ile dönüş almayı sağlar.
Kaynak Kitaplar
10. sınıf matematik ders kitabı, ders notları, okulun belirlediği yardımcı kitaplar, 9. sınıf soru bankaları
BHL-206 Matematik
Ölçme ve Değerlendirme
Matematik dersi ölçme ve değerlendirme sistemi aşağıdaki kriterlere göre yapılandırılmıştır;




Yazılı sınav sonuçları
Proje / Araştırma ödevi
Haftalık ödevler
Genel performans değerlendirmesi
Yazılı sınavlar öğrencilerin dönem süresince gördükleri konulardan derlenen sorularla gerçekleştirilir.
Proje / Araştırma ödevleri ise belirtilen konulardan, öğrenciler tarafından seçilen konunun hazırlanarak belirlenen tarihte
teslim edilmesi ile gerçekleştirilir. Öğrencilerin grup halinde veya bireysel olarak istedikleri bir alan veya konuda inceleme,
araştırma ve yorum yapma, görüş geliştirme, yeni bilgilere ulaşma, özgün düşünce üretme ve çıkarımlarda bulunmaları
amacıyla ders öğretmeni rehberliğinde yapacakları çalışmalardır.
Haftalık ödevler ise belirli ölçütlere göre değerlendirilen öğrenme etkinlikleridir. Haftalık ya da birden fazla haftanın ölçme
değerlendirme anlamında takibini hedefleyen yazılı ya da sözlü ödevlerdir.
Genel performans değerlendirmesi ise öğrencinin sahip olduğu bilgi, beceri, yetenek ve tutumları, kulüp çalışmalarına
katılımı, genel davranış eğilimleri, iletişim becerileri, derse aktif olarak katılımı, Ders araç- gereçlerinin eksiksiz hazırlığı ve
kıyafet koduna uyumunun göz önüne alındığı değerlendirmelerdir.




Öğrencilerin karnesine yansıyacak notları; bir dönem içinde uygulanan yazılıların sonuçları, verilen performans
çalışmalarının sonuçları, sınıf içindeki derse katılım durumları, ders araç gereçlerini bulundurmalarına bağlı olarak
belirlenecektir.
Yapılan değerlendirmelerdeki sorular çoktan seçmeli ve klasik sorulardan oluşacaktır.
Proje ödevleri de not değerlendirilmesi kapsamında önemli bir yere sahiptir. Belirtilen konulardan, öğrenciler
tarafından seçilen konu hazırlanarak belirlenen tarihte teslim edilmelidir.
Proje ödevleri; Kasım ayının 2. Haftasında verilecek ve Nisan ayının 4. Haftasında toplanacaktır.
Proje / Araştırma Ödev Konuları
1. Sıralama ve Seçme
2. Koşullu Olasılık
3. Fonksiyonlarla İşlemler
4. Fonksiyonların Simetrileri ve Cebirsel Özellikleri
5. İki Fonksiyonun Bileşkesi ve Bir Fonksiyonun Tersi
6. Fonksiyonlarla ilgili Uygulamalar
7. Doğrunun Analitik İncelenmesi
8. Dörtgenler ve Özellikleri
9. Özel Dörtgenler
10. Çokgenler
11. İkinci Dereceden Bir Bilinmeyenli Denklemler
12. İkinci Dereceden Fonksiyonlar ve Grafikleri
13. Polinom Kavramı ve Polinomlarla İşlemler
14. Polinomlarda Çarpanlara Ayırma
15. Polinom ve Rasyonel Denklemlerin Çözüm Kümeleri
16. Çember Ve Daire
17. Çemberde Açılar
18. Çemberde Teğet
19. Dairenin Çevresi ve Alanı
20. Katı Cisimlerim Yüzey Alanları ve Hacimleri
BHL-206 Matematik
Yazılı Sınavlarda Uyulması Gereken Kurallar



10. sınıflarda ders yılı süresince her yarıyılda 2 sınav dönemi vardır.
Ders yılı içinde yapılacak bütün sınavlar Bölüm/ Zümre Başkanları ve Müdür Yardımcıları tarafından belirlenir.
Sınav Takvimi dönemlik olarak sınıflarda, sınıfların bulunduğu idari panolarda ve web sayfasında ilan edilir.
1. Öğrenciler sınav için sınav saatinden önce sınıflarında, sınav düzeninde hazır bulunur. Sınavda gözcü olan öğretmen, gerek
gördüğünde öğrencilerin oturma düzenini ve yerlerini değiştirebilir.
2. Öğrenciler sınavda kalem, silgi, cetvel vs. gibi dersin türüne göre değişen araç-gereçlerini ve bunların yedeklerini
bulundurmak zorundadır. Sınav sırasında diğer öğrencilerden bu araçlar istenmez veya ortak kullanılmaz.
3. Ortak sınavlar o dersin öğretmeni tarafından yapılmayabilir. Sınavı bir başka öğretmen de uygulayabilir.
4. Sınav sırasında konuşulmaz ve diğer öğrenciler rahatsız edilmez.
5. Öğrenciler sınav kâğıdı üzerinde bulunan sınavla ilgili açıklamaları dikkatle okumakla, bu konuda yapılan sözlü açıklamaları
dikkatle dinlemekle ve uygulamakla yükümlüdürler. Bu açıklamalara uymayan öğrencilerin yanıtları değerlendirilmez.
6. Sınav sırasında her ne sebeple ve her ne konuda olursa olsun konuşmak, bir başkasının kâğıdına bakmak veya kâğıdını bir
başkasının görebileceği konumda tutmak yasaktır.
7. Önceden bildirilen sınav süresi bitiminde öğrenciler soru ve yanıt kâğıtlarını anında ve istenilen düzende teslim etmek
zorundadırlar. Aksi davranışta bulunan öğrencinin sınavı iptal edilir.
8. Sınav kâğıdını teslim eden öğrenci ders zili çalmadıkça dışarı çıkamaz ve sınav düzenini bozamaz.
9. Sınava ek süre verilmişse ders zili çaldığında dışarı çıkmasına izin verilen öğrenci sınav odasından uzaklaşır, sınavı devam
eden dersliklerin önünde duramaz veya herhangi bir nedenle tekrar içeriye giremez.
10. Sınav kâğıdına yanıtların dışında hiçbir şey yazılamaz.
11. Raporlu ya da izinli olduğu için sınava giremeyen öğrenciler telafi sınavı için belirtilen gün, saat ve yerde bulunmak
zorundadırlar.
12. Sınavlarda kopya çekildiği tespit edildiğinde ve sınav kurallarına uyulmadığında öğrencinin yazılı sınavı iptal edilerek,
öğrenci disiplin kuruluna sevk edilecektir.
10.SINIF MATEMATİK DERSİ HAFTALARA GÖRE KONU DAĞILIMI
10. sınıfta yer alan öğrenme alanları aracılığı ile öğrencilerin aşağıdaki kazanımlara ulaşmaları beklenmektedir:
Sayılar ve Cebir
• Polinom ve polinomlarla yapılan işlemleri ve rasyonel denklem kavramlarını açıklama
• İkinci dereceden denklem kavramını açıklama ve denklemin köklerini bulma ve gerçek yaşam problemlerinin çözümünde
kullanma
• İkinci dereceden bir fonksiyonun grafik gösteriminde, katsayılardaki değişimin grafik gösteriminde meydana getirdiği
değişiklikleri gerekçeleriyle açıklama ve bu süreçte bilgi ve iletişim teknolojilerini etkili kullanma
• Gerçek sayılar kümesinin yeterli olmadığı durumları örneklendirerek karmaşık sayılara olan gereksinimi fark etme
Geometri
• İki değişken arasındaki doğrusal ilişkiyi gösterme ve bunu koordinat düzleminde temsil etme
• Çemberin temel ve yardımcı elemanlarını ve bunlar arasındaki ilişkileri neden-sonuç ilişkisi içerisinde açıklama
• Dörtgenlerin özelliklerini neden-sonuç ilişkisi içerisinde ele alma
• Dörtgenlerin alan bağıntılarını problem çözme sürecinde kullanma
• Özel dörtgenlerin kendi içerisindeki hiyerarşik ilişkisini anlama
• Dik prizma, dik piramit, dik dairesel silindir ve dik dairesel koninin yüzey alan ve hacim bağıntılarını gerçek yaşam
problemlerini modellemede ve problem çözmede kullanma
Veri, Sayma ve Olasılık
• Çeşitli olayların gerçekleşme sayılarını, nesnelerin kendi aralarında farklı şekillerde sıralanma sayılarını ve belli bir nesne
arasından belli şartları sağlayanların seçilme sayısını hesaplama
• Bağımlı ve bağımsız olayları ayırt ederek verilen koşullar altında tanımlanan bir olayın gerçekleşme olasılığını hesaplama
BHL-206 Matematik
Haftalık Ders Konuları
1. ÜNİTE: VERİ, SAYMA
1.HAFTA KONU: Sıralama ve Seçme
2.HAFTA KONU: Pascal özdeşliği ve Binom teoremi
2. ÜNİTE: OLASILIK
3.HAFTA KONU: Koşullu Olasılık- Bileşik olasılık
3. ÜNİTE: FONKSİYONLARLA İŞLEMLER VE UYGULAMALARI
4.HAFTA KONU: Fonksiyonlarla İşlemler ve Uygulamaları
5.HAFTA KONU: Fonksiyonların Simetrileri ve Cebirsel Özellikleri
6.HAFTA KONU: İki Fonksiyonun Bileşkesi
7.HAFTA KONU: Bir Fonksiyonun Tersi
8.HAFTA KONU: Fonksiyonlarla İlgili Uygulamalar
9.HAFTA KONU: Fonksiyonlarla İlgili Uygulamalar
4.ÜNİTE: ANALİTİK GEOMETRİ
10. HAFTA KONU: Doğrunun Analitik İncelenmesi
11. HAFTA KONU: Doğrunun Analitik İncelenmesi
5.ÜNİTE: DÖRTGENLER VE ÇOKGENLER
12.HAFTA KONU: Dörtgenler ve Çokgenler- Dörtgenler ve Özellikleri
13.HAFTA KONU: Özel Dörtgenler-Yamuk ile ilgili açı, kenar ve köşegen özellikleri
14.HAFTA KONU: Özel Dörtgenler- paralelkenar ile ilgili açı, kenar ve köşegen özellikleri
15.HAFTA KONU: Özel Dörtgenler- eşkenar dörtgen ile ilgili açı, kenar ve köşegen özellikleri
16.HAFTA KONU: Özel Dörtgenler- dikdörtgen ve kare ile ilgili açı, kenar ve köşegen özellikleri
17.HAFTA KONU: Özel Dörtgenler- deltoid ile ilgili açı, kenar ve köşegen özellikleri
18.HAFTA KONU: Çokgenler
6.ÜNİTE: İKİNCİ DERECEDEN DENKLEM VE FONKSİYONLAR
19.HAFTA KONU: İkinci Dereceden Bir Bilinmeyenli Denklemler
20.HAFTA KONU: İkinci Dereceden Bir Bilinmeyenli Denklemler
21.HAFTA KONU: Karmaşık sayılar
22.HAFTA KONU: İkinci dereceden bir bilinmeyenli denklemin kökleri, katsayıları-İkinci Dereceden Fonksiyonlar ve Grafikleri
23.HAFTA KONU: İkinci Dereceden Fonksiyonlar ve Grafikleri
24.HAFTA KONU: İkinci Dereceden Fonksiyonlar ve Grafikleri
7.ÜNİTE: POLİNOMLAR
25.HAFTA KONU: Polinom Kavramı ve Polinomlarla İşlemler
26.HAFTA KONU: Polinom Kavramı ve Polinomlarla İşlemler
27.HAFTA KONU: Polinom Kavramı ve Polinomlarla İşlemler
28.HAFTA KONU: Polinom Kavramı ve Polinomlarla İşlemler-Polinomlarda Çarpanlara Ayırma
29.HAFTA KONU: Polinomlarda Çarpanlara Ayırma
30.HAFTA KONU: Polinomlarda Çarpanlara Ayırma
31.HAFTA KONU: Polinom ve Rasyonel Denklemlerin Çözüm Kümeleri
8.ÜNİTE: ÇEMBER VE DAİRE
32.HAFTA KONU: Çemberin Temel Elemanları- Çemberde Açılar
33.HAFTA KONU: Çemberde Açılar-Çemberde Teğet
34.HAFTA KONU: Dairenin Çevresi ve Alanı
9.ÜNİTE: GEOMETRİK CİSİMLER
35.HAFTA KONU: Katı Cisimlerin Yüzey Alanları ve Hacimleri
36.HAFTA KONU: Katı Cisimlerin Yüzey Alanları ve Hacimleri
BHL-206 Matematik
1. ÜNİTE: VERİ, SAYMA
1.HAFTA
KONU: Sıralama ve Seçme

Olayların gerçekleşme sayısını toplama ve çarpma prensiplerini kullanarak hesaplar.

Sınırsız sayıda tekrarlayan nesnelerin dizilişlerini (permütasyonlarını) örneklerle açıklar.
Soru 1: Gençlik ve Spor Bayramı etkinliği yapılan bir statta halk oyunları gösterisi yapan 20, akrobasi hareketleri yapan 6,
voleybol oynayan 8,futbol oynayan 10 öğrenci bulunduğuna göre bu etkinlikte gösteri yapan kaç öğrenci vardır?
Soru 2: 6 farklı gömleği ve 4 farklı pantolonu olan bir kişi bu kıyafetler arasından 1 gömlek ve 1 pantolonu kaç farklı şekilde
seçebilir?
Soru 3: Spor toto oyununda ilk on uç maçın hepsini de doğru tahmin etmek için birbirinden farklı en az kaç tane kolon
oynamak gerekir?
Soru 4: T = 1! + 2! + 3! + ... + 100! sayısının birler basamağında hangi rakam vardır?
Soru 5: 3.P(2n,1)= 2.P(n,2) eşitliğini sağlayan n sayısı kaçtır?
2.HAFTA
KONU: Pascal özdeşliği ve Binom teoremi




n elemanlı bir kümenin r tane elemanının kaç farklı şekilde seçilip sıralanabileceğini hesaplar.
n elemanlı bir kümenin r tane elemanının kaç farklı şekilde seçilebileceğini hesaplar.
Pascal özdeşliğini gösterir ve Pascal üçgenini oluşturur.
Binom teoremini açıklar ve açılımdaki katsayıları Pascal üçgeni ile ilişkilendirir.
Soru 1: İçlerinde Kemal’in de bulunduğu 8 kişilik bir gruptan;
a) 3 kişilik komisyon,
b) Kemal’in de bulunduğu 3 kişilik komisyon kaç farklı şekilde seçilebilir?
Soru 2:
Şekildeki üçgen üzerinde gösterilen noktalardan kaç farklı doğru geçer?
Soru 3: Bir düzlemde 5 paralel doğru ile bunlara dik 4 paralel doğru kaç dikdörtgen oluşturur?
Soru 4:
ifadesinin x in azalan kuvvetlerine göre açılımında x6 lı terim baştan kaçıncı terimdir?
Soru 5: (x2 + 2y)4 ifadesinin açılımını bulalım.
Soru 6: (x – y)n ifadesinin açılımında 11 tane terim olduğuna göre, n ε N sayısını bulalım.
BHL-206 Matematik
2. ÜNİTE: OLASILIK
3.HAFTA
KONU: Koşullu Olasılık

Koşullu olasılığı örneklerle açıklar.

Bağımlı ve bağımsız olayları örneklerle açıklar; gerçekleşme olasılıklarını hesaplar.
Soru 1: Çift zar atıldığında üste gelen sayıların aynı olduğu bilindiğine göre zarların ikisinin de 6 gelme olasılığını bulalım.
Soru 2: Bir çift zar atılıyor. Üste gelen yüzlerin toplamının 7 den büyük olduğu bilindiğine göre toplamın 4 ile bölünebilme
olasılığı kaçtır?
Soru 3: A ve B, E örnek uzayının herhangi iki olayı olsun. P(A) = 2/5, P(A∩B) = 4/5 ve P(B) = x olduğuna göre;
A. A ve B bağımsız olaylar ise x kaçtır?
B. A ve B ayrık olaylar ise x kaçtır? Bulalım.
Soru 4: Bir zar ve bir madeni para birlikte atıldığında paranın tura ve zarın tek sayı gelme olasılığını bulalım.
KONU: Bileşik olasılık

Bileşik olayların olasılıklarını hesaplar.
Soru 1: Bir torbada aynı büyüklükte 4 mavi, 3 kırmızı ve 5 sarı bilye vardır. Torbadan çekilen bilyeler tekrar torbaya
atılmadığına göre, üst üste 3 bilye çekilirse 3 bilyenin de sarı renkli olma olasılığı kaçtır?
Soru 2: Üç kutudan birincisinde 4 sarı, 6 yeşil bilye, ikinci kutuda 3 sarı, 5 yeşil bilye ve üçünü kutuda 2 sarı, 3 yeşil bilye
vardır. Rastgele bir kutu ve sonra da bu kutudan bir bilye çekiliyor. Çekilen bu bilyenin sarı olma olasılığını bulalım.
Soru 3: bir torbada 5 mavi, 4 kırmızı ve 3 yeşil bilye vardır. Ardarda çekilen 3 bilyeden 2 sinin mavi 1 inin yeşil olma olasılığı
kaçtır?
Soru 4:
A, B, C gibi üç şehirden A şehrinden B şehrine gitmek için 4 yol, B şehrinden C
şehrine gitmek için 3 yol ve A şehrinden C şehrine B ye uğramadan gidilebilen 3
yol vardır. Buna göre A şehrinden C şehrine kaç türlü gidilebilr?
3. ÜNİTE: FONKSİYONLARLA İŞLEMLER VE UYGULAMALARI
4.HAFTA
KONU: Fonksiyonların Simetrileri ve Cebirsel Özellikleri

Bir fonksiyonun grafiğinden, simetri dönüşümleri yardımı ile yeni fonksiyon grafikleri çizer.
Soru 1: f(x) = x2 fonksiyonu verilsin.
a. f(x) + 2
b. f(x – 2)
c. 2.f(x) ç. f(2x)
d. –f(x)
e. f(–x) fonksiyonlarının
grafiğini çizerek bu grafiğin, f(x) = x2 fonksiyonunun grafiğine hangi dönüşüm uygulandığında elde edilebileceğini bulalım.
BHL-206 Matematik
5.HAFTA
KONU: Fonksiyonların Simetrileri ve Cebirsel Özellikleri

Gerçek sayılar kümesinde tanımlı f ve g fonksiyonlarını kullanarak toplama, çıkarma, çarpma, bölme
fonksiyonlarını elde eder.
Soru 1: f: R→R, f(x) = x + 1 ve g: R→R g(x) = 2x fonksiyonları verilsin.
a. f + g b. f – g c. f.g
ç. f/g
fonksiyonlarını bulalım.
6.HAFTA
KONU: İki Fonksiyonun Bileşkesi

Fonksiyonlarda bileşke işlemini açıklar.
Soru 1: f R→R, f(x) = x + 2 ve g: R→R, g(x) = 2x fonksiyonları verilsin.
a. (gof) (x) ve (gof) (2)
b. (fog) (x) ve (fog) (2) değerlerini bulalım.
Soru 2: f ve g fonksiyonları için,
f(x+2)= 2x-2 ve g(2x-5)= 4x-5 ise (gof)-1(1) değeri kaçtır?
7.HAFTA
KONU: Bir Fonksiyonun Tersi

Bir fonksiyonun bileşke işlemine göre tersinin olması için gerekli ve yeterli şartları belirleyerek, verilen bir
fonksiyonun tersini bulur.
Soru 1: A = {–1, 0, 1, 2} olmak üzere f: A → B, f(x) = 2x –1 bire bir ve örten fonksiyonu verilsin. Buna göre f-1: B→ A
fonksiyonunun kuralını bulalım.
Soru 2: f(x)= -2x2+8x-4
(g○f)= x2-4x+2 fonksiyonları veriliyor. Buna göre g(-3) değeri kaçtır?
8.HAFTA
KONU: Fonksiyonlarla İlgili Uygulamalar

İki miktar (nicelik) arasındaki ilişkiyi fonksiyon kavramıyla açıklar; problem çözümünde fonksiyonun grafik ve tablo
temsilini kullanır.
Soru 1: (fog) (x) = 2x2 – 3 ve f(x) = x + 2 olduğuna göre g(x) fonksiyonunu bulalım.
BHL-206 Matematik
Soru 2: Bir oto kiralama şirketi müşterilerinden kira ücreti olarak 1. gün 60 lira ve daha sonraki her bir gün için 40 lira ücret
talep etmektedir. Buna göre ödenen ücreti, kiralama suresinin (gün) bir fonksiyonu olarak yazıp 1 haftalık kira ücretinin kaç
lira olduğunu bulalım.
9.HAFTA
KONU: Fonksiyonlarla İlgili Uygulamalar

İki miktar (nicelik) arasındaki ilişkiyi fonksiyon kavramıyla açıklar; problem çözümünde fonksiyonun grafik ve tablo
temsilini kullanır.
Soru 1: Elektrik üreticisi bir firma abonelerinden aylık 1 lira sabit abonman ücreti ve kullanılan her kw elektrik için de 0,16
lira kullanım ücreti almaktadır. Buna göre ayda x kw elektrik kullanan bir abonenin fatura ücreti y lira olduğuna göre, x ile y
arasındaki bağıntı hangisidir?
4.ÜNİTE: ANALİTİK GEOMETRİ
10. HAFTA
KONU: Doğrunun Analitik İncelenmesi


Analitik düzlemde iki nokta arasındaki uzaklığı veren bağıntıyı oluşturur ve uygulamalar yapar.
Bir doğru parçasını belli bir oranda (içten veya dıştan) bölen noktanın koordinatlarını hesaplar.
Soru 1: Gerçek sayılar doğrusunda A(–4), B(6) ve C(x) noktaları verilsin. |AC| = |CB| ise x ε R sayısını bulalım.
Soru 2: A(–2, 6) ve B(6, 12) noktaları arasındaki uzaklık kaç birimdir?
Soru 3: Analitik düzlemde A(1, 2) ve B(3, 0) noktaları veriliyor. [AB] nı CA/CB=5/3 oranında dıştan bölen C noktasının
koordinatlarını ve |AC| ile |BC| nu bulalım.
11. HAFTA
KONU: Doğrunun Analitik İncelenmesi



Bir doğru parçasını belli bir oranda (içten veya dıştan) bölen noktanın koordinatlarını hesaplar.
Analitik düzlemde doğru denklemini oluşturur ve denklemi verilen iki doğrunun birbirine göre durumlarını inceler.
Bir noktanın bir doğruya uzaklığını açıklar ve uygulamalar yapar.
Soru 1: Köseleri, A(–6, 7), B(–3, 6) ve C(3, 2) olan ABC üçgeni veriliyor. Bu üçgenin ağırlık merkezinin başlangıç noktasına
uzaklığı kaç birimdir?
Soru 2: Analitik düzlemde A(2, 0) ve B(4, 2) noktalarından gecen doğrunun eğimini ve eğim açısının ölçüsünü bulalım.
Soru 3: A(–1, –2) ve B(2, 1) noktalarından gecen doğrunun denklemini bulalım.
Soru 4: d1: 2x – y + 3 = 0 ve d2: ax + 3y – 2 = 0 doğruları birbirine dik olduğuna göre, a ε R sayısını bulalım.
Soru 5: Analitik düzlemde A(–2, 2) ve B(0, 4) noktaları veriliyor. [AB] nın orta dikme doğrusunun denklemini bulunuz.
Soru 6: A(5, –3) noktasının d: 3x – 4y + 8 = 0 doğrusuna olan uzaklığını bulalım.
BHL-206 Matematik
5.ÜNİTE: DÖRTGENLER VE ÇOKGENLER
12.HAFTA
KONU: Dörtgenler ve Çokgenler- Dörtgenler ve Özellikleri

Dörtgenin temel elemanlarını ve özelliklerini açıklar.
Soru 1: ABCD dörtgeninde köşegen uzunlukları |AC| = 4 √3 cm, lBDl = 6 cm ve köşegenler arasındaki açının ölçüsü 60° ise bu
dörtgensel bölgenin alanını bulalım.
13.HAFTA
KONU: Özel Dörtgenler-Yamuk ile ilgili açı, kenar ve köşegen özellikleri


Yamuk ile ilgili açı, kenar ve köşegen özelliklerini açıklar.
Yamuk alan bağıntılarını oluşturur.
Soru1: Köşegenleri dik kesişen bir ABCD yamuğunda; [AB] // [CD], |AC| = 12 cm, |BD| = 16 cm olduğuna göre, orta taban
uzunluğu kaç cm dir?
Soru 2: Aşağıdaki ifadeler doğru ise yay ayraç içine “D”, yanlış ise “Y” yazınız.
( ) Bir yamuğun alanı orta taban uzunluğu ile yüksekliğinin çarpımına eşittir.
( ) Her dörtgende olduğu gibi yamukta da kenarların orta noktalarını köşe kabul eden dörtgenin alanı, yamuğun
alanının yarısıdır.
Soru 3:
Şekildeki ABCD yamuğunda; [AB]//[DC] dir. m(B)= x+40, m(C)= 3x, m(D)= 3x+20 ise m(A)
kaçtır?
14.HAFTA
KONU: Özel Dörtgenler- paralelkenar ile ilgili açı, kenar ve köşegen özellikleri


Paralelkenar ile ilgili açı, kenar ve köşegen özelliklerini açıklar.
Paralelkenar alan bağıntılarını oluşturur.
Soru 1: Aşağıdaki ifadeler doğru ise yay ayraç içine “D”, yanlış ise “Y” yazınız.
( ) Karşılıklı açıları eş olan her dörtgen paralelkenardır.
( ) Köşegenleri birbirini ortalayan her dörtgen paralelkenardır.
( ) Bir dörtgende karşılıklı iki kenar hem paralel hem de eş ise bu dörtgen paralelkenardır.
( ) Paralelkenar bir köşegeni ile eşit alanlı iki üçgene ayrılır.
( ) Paralelkenarın her iki köşegeni de çizilirse eşit alanlı dört üçgen elde edilir.
BHL-206 Matematik
Soru 2:
Şekildeki ABCD paralelkenarında m(D)= 5x-20 ve m(C)= 2x-10 olduğuna göre m(A) kaç
derecedir?
15.HAFTA
KONU: Özel Dörtgenler- eşkenar dörtgen ile ilgili açı, kenar ve köşegen özellikleri


Eşkenar dörtgen ile ilgili açı, kenar ve köşegen özelliklerini açıklar.
Eşkenar dörtgen alan bağıntılarını oluşturur.
Soru 1: Aşağıdaki ifadeler doğru ise yay ayraç içine “D”, yanlış ise “Y” yazınız.
( ) Eşkenar dörtgenin alanı köşegen uzunlukları çarpımının yarısıdır.
( ) Eşkenar dörtgende köşegenler diktir.
( ) Eşkenar dörtgende köşegenler açıortaydır ve birbirini dik ortalar.
( ) Tüm kenarları eş olan paralelkenara eşkenar dörtgen denir.
Soru 2:
Bir kenar uzunluğu 13 cm olan eşkenar dörtgenin yüksekliği 5 cm ise kısa
köşegenin uzunluğu kaç cm’dir?
16.HAFTA
KONU: Özel Dörtgenler- dikdörtgen ve kare ile ilgili açı, kenar ve köşegen özellikleri


Dikdörtgen ve kare ile ilgili açı, kenar ve köşegen özelliklerini açıklar.
Dikdörtgen ve kare alan bağıntılarını oluşturur.
Soru 1: Aşağıdaki ifadeler doğru ise yay ayraç içine “D”, yanlış ise “Y” yazınız.
( ) Karede köşegenler diktir ve birbirini ortalar.
( ) Kare bir dikdörtgendir.
( ) Karede her iki köşegen de açıortaydır.
Soru 2:
Şekildeki ABCD dikdörtgendir. │EA│= 3x-1 birim, │EC│= x+4 birim, │AB│= a birim,
│BC│= b birim ve a.b= 60 ise ABCD dikdörtgeninin çevresi kaç birimdir?
Soru 3:
Şekildeki ABCD kare ve AEFC dikdörtgendir. ABCD karesinin bir kenar uzunluğu
ise AEFC dikdörtgeninin çevre uzunluğu kaç cm’dir?
BHL-206 Matematik
17.HAFTA
KONU: Özel Dörtgenler- deltoid ile ilgili açı, kenar ve köşegen özellikleri


Deltoid ile ilgili açı, kenar ve köşegen özelliklerini açıklar.
Deltoid alan bağıntılarını oluşturur.
Soru 1: Aşağıdaki ifadelerde boş bırakılan yerlere uygun kelimeleri yazınız.
Deltoidde köşegenler birbirine ………………
Deltoidin iki iç açı ölçüsü ……………………….
Soru2:
ABCD deltoidinde m(KDC)= 50 m(A)= 2.m(C)+10 ise A açısının ölçüsü kaç
derecedir?
18.HAFTA
KONU: Özel Dörtgenler- deltoid ile ilgili açı, kenar ve köşegen özellikleri

Dörtgenlerin alan bağıntılarını modelleme ve problem çözmede kullanır.
Soru1:
ABCD dörtgeninde S1, S2, S3, S4, içinde bulundukları bölgelerin alanlarını
göstermektedir. S2 = 4S1, S1.S4 =128, S3= 64 cm2 ise A(ABCD) kaç cm2 dir?
Soru 2:
Şekildeki ABCD paralelkenarında │EF│=│FC│, │AE│=│EB│ ve taralı alan 60 br2 ise
A(ABCD) kaç br2 dir?
KONU: Çokgenler

Çokgenleri açıklar, iç ve dış açılarının ölçülerini hesaplar.
Soru 1:
ABCDEF bir düzgün altıgen olduğuna göre m(CKF)= α kaç derecedir?
BHL-206 Matematik
Soru 2: İç açı ölçülerinin aritmetik ortalaması 150° olan bir çokgen kaç kenarlıdır?
Soru 3: Bir dışbükey çokgende üç tane iç açı ölçüsü 100, 110 ve 120 derecedir. Diğer iç açılar birbirine eş ve ölçüleri 150°
olduğuna göre bu çokgen kaç kenarlıdır?
Soru 4: Bir iç açısının ölçüsü 150° olan düzgün çokgen kaç kenarlıdır?
6.ÜNİTE: İKİNCİ DERECEDEN DENKLEM VE FONKSİYONLAR
19.HAFTA
KONU: İkinci Dereceden Bir Bilinmeyenli Denklemler

İkinci dereceden bir bilinmeyenli denklemleri çözer.
Soru 1: x2 – 4x + 3 = 0 denklemini çözelim.
Soru 2: (m + 1) x2 + 2mx – 3(m + 3) = 0 denkleminin köklerinden biri 2 olduğuna göre diğer kökün kaç olduğunu bulalım.
20.HAFTA
KONU: İkinci Dereceden Bir Bilinmeyenli Denklemler

İkinci dereceden bir bilinmeyenli denklemleri çözer.
Soru 1: x2 + (m – 2) x + 9 – 2m = 0 çakışık iki kökü olduğuna göre m sayısını bulunuz.
21.HAFTA
KONU: Karmaşık sayılar

i sanal birim olmak üzere bir karmaşık sayının a + bi biçiminde ifade edildiğini açıklar.
Soru 1: i89 sayısının değerini bulalım.
Soru 2: Karmaşık sayılar kümesinde z2 – 4z + 13 = 0 denkleminin köklerini bulalım.
Soru 3: z1 = 2 – 3i ve z2 = 1 + i olduğuna göre, z1 + z2 ve z1 – z2 sayılarını bulalım.
22.HAFTA
KONU: İkinci dereceden bir bilinmeyenli denklemin kökleri ile katsayıları

İkinci dereceden bir bilinmeyenli denklemin kökleri ile katsayıları arasındaki ilişkileri belirler.
KONU: İkinci Dereceden Fonksiyonlar ve Grafikleri

İkinci dereceden bir değişkenli fonksiyonu açıklar ve grafiğini çizer.
BHL-206 Matematik
Soru 1: 2x2 – 3x – 1 = 0 denkleminin kökler toplamını ve çarpımını bulalım.
Soru 2: Sanal köklerinden biri z = 2 – 3i olan gerçek katsayılı ikinci dereceden denklemi yazınız.
Soru 3: x2 – 2x + c = 0 denkleminin kökleri x1 ve x2 dir. 3x1 – x2 = 6 olduğuna göre c ε R sayısını bulalım.
23.HAFTA
KONU: İkinci Dereceden Fonksiyonlar ve Grafikleri

İkinci dereceden bir değişkenli fonksiyonu açıklar ve grafiğini çizer.
Soru 1: Eksenleri (1, 0) , (5, 0) ve (0,–5) noktalarında kesen parabolün denklemi hangisidir?
Soru 2: Tepe noktası T(1, 0) olan ve A(0,–1) noktasından geçen parabolün denklemi hangisidir?
Soru 3: f(x) = x2 – 2x + 6 fonksiyonunun y = a(x – r) + k biçimindeki yazılışı aşağıdakilerden hangisidir?
24.HAFTA
KONU: İkinci Dereceden Fonksiyonlar ve Grafikleri


İkinci dereceden bir değişkenli fonksiyonu açıklar ve grafiğini çizer.
İkinci derece denklem ve fonksiyonlarla modellenebilen problemleri çözer.
Soru 1: Dikdörtgen biçimindeki bir arsanın çevresi 120 m olduğuna göre bu arsanın alanı en çok kaç m2 olabilir?
Soru 2: İki musluk birlikte açıldığında boş bir havuz 6 saatte dolmaktadır. Birinci musluğun bu havuzu doldurma süresi, ikinci
musluğun doldurma süresinden 5 saat fazla olduğuna göre ikinci musluk bu boş havuzu kaç saatte doldurur?
7.ÜNİTE: POLİNOMLAR
25.HAFTA
KONU: Polinom Kavramı ve Polinomlarla İşlemler

Gerçek katsayılı ve bir değişkenli polinom kavramını açıklar.
Soru 1: p(x) = (a – b – 8) x2 + (b –2) x + a.b sabit bir polinom olduğuna göre p(2) değerini bulalım.
Soru 2: p(x – 1) = (x – 1)4 + 4x2 – 8x – 2 ise p(x) polinomunu bulalım.
Soru 3: p(x) = 1 – 3x + 4x2 + 5x3 – 6x4 polinomunda p(0) + p(1) toplamını bulalım.
26.HAFTA
KONU: Polinom Kavramı ve Polinomlarla İşlemler

Polinomlarla toplama, çıkarma, çarpma ve bölme işlemlerini yapar.
BHL-206 Matematik
Soru 1: p(x) = –1 + 3x – x2 + 2x3 ve q(x) = 2 + x + 3x2 ise p(x) + q(x) polinomunu bulalım.
Soru 2: p(x) = –3 + 4x – 3x3 + 2x4 ve q(–x) = 3 – x2 + x3 + x4 ise p(x) – q(x) polinomunu bulalım.
Soru 3: p(x + 2) + p(x – 1) = 8x2 + 2x + 1 olduğuna göre, p(x) polinomunu bulalım.
27.HAFTA
KONU: Polinom Kavramı ve Polinomlarla İşlemler

Bir p(x) polinomunun q(x) polinomuna bölümünden kalanı bulur.
Soru 1: p(x) = 2 + 16x – x2 – 4x3 + x4 polinomunu q(x) = x2 – x polinomuna bölelim.
Soru 2: p(x) = x4 – 3x3 + 2x2 + x – 1 polinomunun (x + 2) ile bölümünden kalanı bulalım.
Soru 3: p(x) = 2x5 + 3x4 –4x3 + 5x2 – 6x polinomunun (x2 – 1) ile bölümünden elde edilen kalanı bulalım.
28.HAFTA
KONU: Polinom Kavramı ve Polinomlarla İşlemler

Katsayıları tam sayı ve en yüksek dereceli terimin katsayısı 1 olan polinomların tam sayı sıfırlarının, sabit terimin
çarpanları arasından olacağını örneklerle gösterir.
KONU: Polinomlarda Çarpanlara Ayırma

Gerçek katsayılı bir polinom çarpanlarına ayırır.
Soru 1: Kökleri –1, 1 ve –2 olan üçüncü dereceden ve baş katsayısı 1 olan bir polinom yazalım.
Soru 2: p(x) = x3 – 6x2 + 11x – 6 polinomunun köklerini bulalım.
Soru 3: p(x) = 4x2 – 9 polinomunu çarpanlarına ayıralım.
29.HAFTA
KONU: Polinomlarda Çarpanlara Ayırma

Gerçek katsayılı bir polinomu çarpanlarına ayırır.
Soru 1: 3a2 + 2ab + 6a + 4b ifadesinde bazı terimleri gruplandırarak ortak çarpan yardımıyla çarpanlara ayıralım.
Soru 2: 4x3 – 8x2 – x + 2 ifadesini gruplandırarak çarpanlarına ayıralım.
30.HAFTA
KONU: Polinomlarda Çarpanlara Ayırma
BHL-206 Matematik

Gerçek katsayılı bir polinomu çarpanlarına ayırır.
Soru 1: 3x4 – 6x3y + 3x2y2 – 3x2y4 ifadesini özdeşliklerden faydalanarak çarpanlarına ayıralım.
Soru 2: p(x) = x2 – 12x + 20 polinomunu çarpanlarına ayıralım.
31.HAFTA
KONU: Polinom ve Rasyonel Denklemlerin Çözüm Kümeleri


Rasyonel ifade kavramını örneklerle açıklar ve rasyonel ifadelerin sadeleştirilmesi ile ilgili uygulamalar yapar.
Polinom ve rasyonel denklemlerle ilgili uygulamalar yapar.
Soru 1:
eşitliği veriliyor. P(x) polinomunun x ile bölümünden kalan 4 olduğuna göre
Q(x) polinomunun (x- 4) ile bölümünden kalan kaçtır?
Soru 2:
ise A.B çarpımı kaçtır?
8.ÜNİTE: ÇEMBER VE DAİRE
32.HAFTA
KONU: Çemberin Temel Elemanları


Çemberlerde teğet, kiriş, çap ve yay kavramlarını açıklar.
Çemberde kirişin özelliklerini gösterir.
Soru 1: Aşağıdaki ifadelerde boş bırakılan yerlere uygun kelimeleri yazınız.
Çember içindeki bir P noktasından gecen en kısa kiriş, P den gecen çapa .............................
Çemberin merkezinden bir kirişine indirilen dikme kirişi ve kirişin yayını ..............................
Merkezden eşit uzaklıktaki kirişler .....................
Çemberde eş kirişlerin yayları da .....................
Çemberde en uzun kiriş .....................
KONU: Çemberde Açılar

Bir çemberde merkez, çevre, iç, dış ve teğet-kiriş açıları açıklar; bu açıların ölçüleri ile gördükleri yayların ölçülerini
ilişkilendirir.
Soru 1: Aşağıdaki ifadelerde boş bırakılan yerlere uygun kelimeleri yazınız.
Bir çemberde çapı gören çevre açının ölçüsü ……………………
Çemberde paralel kirişler arasında kalan yayların ölçüsü ……………………
Aynı yayı gören çevre açı ve teğet kiriş açılar …………………
Soru 2:
Şekildeki O merkezli çemberde m(AOB)= 20 ve m(ACO)= 15 olduğuna göre m(A) kaç derecedir?
BHL-206 Matematik
Soru3:
[PT ile [PL çembere teğettir. m(LAT)= 110 olduğuna göre m(LPT)= x kaç derecedir?
33.HAFTA
KONU: Çemberde Açılar

Bir çemberde merkez, çevre, iç, dış ve teğet-kiriş açıları açıklar; bu açıların ölçüleri ile gördükleri yayların ölçülerini
ilişkilendirir.
Soru 1:
Şekilde [AB] ve [BC] çaplı yarım çemberler B noktasında teğettirler. [CD], [AB]
çaplı çembere D noktasında teğettir. m(EBC)= 40 olduğuna göre m(A)=α kaç
derecedir?
Soru 2:
[AB] çaplı çemberde; [DC]//[AB] m(CEB)= 40 ise m(DEC)= x kaç derecedir?
KONU: Çemberde Teğet

Çemberde teğetin özelliklerini gösterir.
Soru 1: Birbirine teğet iki çemberin değme noktaları ile merkezleri aynı doğru üzerindedir, gösterin.
Soru 2:
O merkezli yarım çembere [BC], [CD] ve[DA] teğettir. │BC│=8, │DA│=2 olduğuna göre
çemberin yarıçapı kaçtır?
Soru 3:
d1 doğrusu A ve B noktasında O1 ve O2 merkezli çembere teğettir. [AH]
[BK] [DC], │AH│+ │BK│= 10 br olduğuna göre │AB│ kaç birimdir?
34.HAFTA
KONU: Dairenin Çevresi ve Alanı

Dairenin çevresini ve alanını veren bağıntılar oluşturur ve uygulamalar yapar.
[DC]
BHL-206 Matematik
Soru 1: O merkezli r = 3 cm yarıçaplı bir çemberde ölçüsü 60° olan AOB açısının gördüğü yayın uzunluğunu bulalım.
Soru 2:
A merkezli çeyrek daire ile O merkezli yarım daire verilmiştir.│BC│=2.│OB│= 4 br dir.
S1 ve S2 bulundukları bölgelerin alanlarını göstermektedir. Buna göre S1 –S2 kaç br2
dir?
9.ÜNİTE: GEOMETRİK CİSİMLER
35.HAFTA
KONU: Katı Cisimlerin Yüzey Alanları ve Hacimleri


Dik prizma ve dik piramitlerin yüzey alan ve hacim bağıntılarını oluşturur.
Dik dairesel silindiri ve dik dairesel koniyi açıklar, yüzey alan ve hacim bağıntılarını oluşturur.
Soru 1: Yanal alanı 45 cm2 ve tabanının bir kenar uzunluğu 3 cm olan eşkenar üçgen dik prizmanın yüksekliği kaç cm dir?
Soru 2: Bir dikdörtgenler prizmasının farklı üç yüzünün alanları 6 cm2, 8 cm2 ve 12 cm2 olduğuna göre bu prizmanın hacmi
kaç cm3 olur?
Soru 3:
Şekildeki üçgen dik prizmada
prizmanın yanal alanı kaç br2 dir?
│AC│= 6 br, │CB│= 8 br, │BB’│= 5 br ise üçgen dik
Soru 4: Tepe noktası T, tabanı ABC eşkenar üçgeni olan (T, ABC) düzgün piramidinde |AB| = |BT| = 6 cm olduğuna göre
piramidin yüksekliği kaç cm dir?
Soru 5: Taban yarıçapı r = 2 cm ve yükseklik uzunluğu h = 4 cm olan dik dairesel silindiri ve açınımını çizelim, yüzey alanını
bulalım.
Soru 6: Bir dik koninin yanal alanı, taban alanının 4 katı olduğuna göre, bu koninin yanal açınımı olan daire diliminin merkez
açısı kaç derecedir?
36.HAFTA
KONU: Katı Cisimlerin Yüzey Alanları ve Hacimleri


Küreyi açıklar, yüzey alanı ve hacim bağıntısını oluşturur.
Katı cisimlerin yüzey alan ve hacim bağıntılarını modelleme ve problem çözmede kullanır.
Soru 1: Bir kürenin merkezinden 3 br uzaklıktaki düzlemsel kesitinin alanı 16π br2 olduğuna göre bu kürenin yüzey alanını
bulalım.
Soru 2:
Yarıçapı 2 cm olan bir kürenin yüzey alanı, yarıçapı 1 cm olan kaç küre yüzey
alanına eşittir?
Soru 3: Taban çapı ve ana doğru parçasının uzunluğu 12 cm olan bir dik dairesel koninin içine yerleştirilecek en büyük
hacimli kürenin alanını ve hacmini bulalım.