T.C
GAZİ ÜNİVERSİTESİ
EĞİTİM BİLİMLERİ ENSTİTÜSÜ
ORTAÖĞRETİM FEN VE MATEMATİK ALANLAR EĞİTİMİ ANABİLİM DALI
KİMYA ÖĞRETMENLİĞİ BİLİM DALI
ENTROPİ VE TERSİNİRLİK KAVRAMLARININ TARTIŞILMASI
YÜKSEK LİSANS TEZİ
Hazırlayan
Sevcan AKMAN
Tez Danışmanı
Prof. Dr. Mehmet Levent AKSU
Ankara-2013
T.C
GAZİ ÜNİVERSİTESİ
EĞİTİM BİLİMLERİ ENSTİTÜSÜ
ORTAÖĞRETİM FEN VE MATEMATİK ALANLAR EĞİTİMİ ANABİLİM DALI
KİMYA ÖĞRETMENLİĞİ BİLİM DALI
ENTROPİ VE TERSİNİRLİK KAVRAMLARININ TARTIŞILMASI
YÜKSEK LİSANS TEZİ
Hazırlayan
Sevcan AKMAN
Tez Danışmanı
Prof. Dr. Mehmet Levent AKSU
Ankara-2013
CANIM KARDEŞİM
ŞEHİT KD. KARA PİLOT ÜSTEĞMEN
YAKUP ÇINAR’IN AZİZ ANISINA
JÜRİ ONAY SAYFASI
Enstitünüze bağlı Ortaöğretim Fen ve Matematik Alanları Eğitimi Bölümü
Yüksek Lisans programında kayıtlı olan 118143117 numaralı Sevcan AKMAN’nın
hazırladığı’’Entropi ve Tersinirlik Kavramlarının Tartışılması” adlı çalışma jürimiz
tarafından Kimya Eğitimi Anabilim Dalında YÜKSEK LİSANS TEZİ olarak kabul
edilmiştir.
i
ÖN SÖZ
Çalışmalarım süresince bilgisi, tecrübesi, güler yüzüyle destek olan ve bana ışık
veren çok sevgili hocam ve danışmanım Prof. Dr. Mehmet Levent AKSU’ ya sonsuz
şükranlarımı sunmayı bir borç bilirim.
Lisans öğrenimimden itibaren her zaman yanımda olan ve desteğini hiç
esirgemeyen can dostum Özlem TÜRK YAVUZ’ a teşekkür ederim.
Ayrıca her ne kadar bu tezden haberleri olmasa da desteklerini her an arkamda
hissettiğim ve ne yapsam haklarını ödeyemeyeceğim annem ve babama büyük minnet
duymaktayım.
Acılarımın ve Rüzgar Masal ile yaşayacağımız güzel günlerin ortağı kız
kardeşim Serpil ÇINAR’a hayatıma kattığı her şey için teşekkür ederim.
En son olarak ta benden habersiz kaydımı yaptıran ve bu tez için bana
motivasyon veren, maddi ve manevi hiçbir fedakarlıktan kaçınmayan eşim Ahmet Şahin
AKMAN’a teşekkür ederim.
Hakkı olan vaktinin büyük bir bölümünü çaldığım canım kızım Ebrar Naz ile
daha fazla ilgilenebileceğimden dolayı çok mutluyum.
ii
ÖZET
Bu araştırma termodinamiğin en karmaşık konusu olan entropi kavramıyla
tersinirlik ve tersinmezlik(kendiğinden olma) konusuna yeni bir anlayış getirmek için
yapılmıştır. Bu amaçla bu konular dünyanın çeşitli fizikokimya kitaplarından taranmış
ve herkese öğretildiği şekilde entropinin artışının hem olayların kendiliğinden olması
yani tersinmezliği ve hem de entropinin bir hal fonksiyonu olduğu hakkındaki
belirsizlik giderilmeye çalışılmıştır. Bu çalışma birçok açıdan klasik eğitim tezlerinden
farklıdır. Burada ne bir ön test metodu alınmış nede bir istatistiksel bir çözümlemeye
gidilmemiştir. Ancak yapılan çalışma bu son derece karmaşık konulara ışık tutacak
niteliktedir.
Anahtar Kelimeler. Entropi, tersinirlik, termodinamiğin II. kanunu
iii
ABSTRACT
This study was carried out to enlighten the most complicated concepts of
thermodynamics entropy and reversibility. For this purpose the subject was thoroughly
investigated from the physical chemistry text books and the subject of entropy as the
parameter of which determines the instantaneous events and the state function property
was thoroughly discussed. This study is different than most of the conventional
education thesis in many respects. There is no pretest post test pattern was employed
and there was no attempt to bring any statistical explanation. This study is expected to
enlighten these complicated and mostly misunderstood concepts.
Keywords: Entrophy, reversibility and the second law of thermodynamics
iv
İÇİNDEKİLER
Sayfa
JÜRİ ÜYELERİNİN İMZA SAYFASI .........................................................................i
ÖN SÖZ ....................................................................................................................... ii
ÖZET .......................................................................................................................... iii
ABSTRACT.................................................................................................................iv
İÇİNDEKİLER .............................................................................................................v
ŞEKİLLERİN LİSTESİ ............................................................................................. vii
1.GİRİŞ
1.1Problem Durumu......................................................................................................1
1.2 Araştırmanın Amacı ................................................................................................ 1
1.3 Araştırmanın Önemi ............................................................................................... 1
1.4 Araştırmanın Sınırlılıkları ....................................................................................... 1
1.5 Varsayımlar .............................................................................................................2
1.6 Tanımlar ..................................................................................................................2
1.6.1.Sistem...................................................................................................................2
1.6.2. İş.......................................................................................................................... 6
1.6.3. Enerji ...................................................................................................................6
2.KAVRAMSAL ÇERÇEVE ....................................................................................... 8
2.1 Tersinirlik ve Tersinmezlik Kavramları .................................................................8
2.2 Termodinamiğin I. Kanunu..................................................................................... 9
2.3 Termodinamiğin II. Kanunu ..................................................................................9
2.3.1 Maksimum İşin Elde Edilmesi ..........................................................................10
2.3.2 Carnot Çevrimi ve Isı Makinaları ......................................................................12
2.4 Entropi Kavramı ...................................................................................................16
2.4.1 Entropinin Fiziksel Anlamı ................................................................................21
2.4.2 Entropinin Bir Hal Fonksiyonu Olması ............................................................. 25
2.4.3Entropinin Bir Hal Fonksiyonu Olduğunun İspatlanması ..................................26
2.5 Clausius Eşitsizliği ................................................................................................ 28
2.6 Minumum Enerji Prensibi ..................................................................................... 29
2.7 Entropinin Artması ( Korunumsuzluğu) Prensibi .................................................29
v
2.7.1 Entropi ve Düzensizlik....................................................................................... 30
3.YÖNTEM ................................................................................................................34
3.1 Araştırma Modeli ..................................................................................................34
3.2 Evren ve Örneklem ............................................................................................... 34
3.3 Veri Toplama Teknikleri ...................................................................................... 34
3.4 Verilerin Analizi ...................................................................................................34
4.BULGULAR ve YORUM ....................................................................................... 35
4.1 Entropiye Moleküler Yaklaşım ve İstatistiksel Termodinamik ............................ 35
5.SONUÇ ve ÖNERİLER .......................................................................................... 42
KAYNAKÇA..............................................................................................................45
vi
ŞEKİLLERİN LİSTESİ
Şekil 1.1 Sistem ve sistemin tipleri ..............................................................................2
Şekil 1.2 Hal Fonksiyonu Olma Şartı ...........................................................................4
Şekil 1.3 Denge ve Şekilleri ........................................................................................ 5
Şekil 1.4 İşin Gösterimi ................................................................................................ 6
Şekil 2.1Tersinir ve Tersinmez Olaylara Bir Örnek ....................................................8
Şekil 2.2 Tek Basamakta Yapılan Tersinmez Genleşme ............................................10
Şekil 2.3 Tek Basamakta Tersinmez Süreçlerde Elde Edilen İşin minimum Olması 11
Şekil 2.4 İki Basmakta Elde edilen İşin Daha Yüksek Olması ...................................11
Şekil 2.5 Sonsuz Basmaklı (Tersinir)Genleşmede Elde Edilen Maksimum İş ..........12
Şekil 2.6 Carnot Çevrimi ............................................................................................ 12
Şekil 2.7 Carnot Makinesinin Şematik Gösterimi ..................................................... 15
Şekil 2.8 Termodinamikte Göz Önüne Alınan Sistem ...............................................16
Şekil 2.9 Termodinamiğin 1. ve 2. Kanununa Göre Olan Olasılıklar ........................ 17
Şekil 2.10 Kentliğinden Olmayan Tersinir Bir Prosesi Dış Bir
Katkı ile Tersine Çevirmek ......................................................................................... 18
Şekil 2.11 Entropinin Grafiksel Olarak Bulunması ................................................... 24
Şekil 2.12 Carnot Çevriminde P-V ve T-S Değişimleri ............................................25
Şekil 2.13 Entropinin Hal Fonksiyon Olduğunun İspatı ............................................26
Şekil 2.14 Entropinin Hal Fonksiyonu Göstermede Alternatif Yöntem ................... 27
Şekil 2.15 Minimum Enerji Prensibi .........................................................................29
Şekil 5.1 Entropinin Negatif Çıkması Durumunda Bile Olayın
Kendiliğinden Olması ..................................................................................42
Şekil 5.2 Ayrışmanın Kendiliğinden Olması .............................................................. 43
vii
1
GİRİŞ
Bu bölümde, araştırmanın problem durumu, amacı ve önemi, problem cümlesi,
alt problemler, sayıltılar, sınırlılıklar, tanımlar ve kısaltmalara yer verilmiştir. Problem
durumunda, termodinamik, termodinamiğin ikinci yasası ve entropi tanıtılmış, önemleri
vurgulanmış termodinamiğin bu çok önemli ve karmaşık fonksiyonu açıklanmaya
çalışılmıştır.
1.1.Problem Durumu
Burada üç tane problem cümlesinin cevabı aranmıştır Bunlar:
1. Entropinin hal fonksiyonu mudur?
2. Kendiliğinden olan her olayda entropi artar mı?
3. Kendiliğinden olan her olayda düzensizlik artar mı?
1.2. Araştırmanın Amacı
Termodinamik konusunda anlaşılması en güç olan kavramlar tersinirlik ve
tersinmezlik kavramalarıyla entropi fonksiyonudur. Bu araştırma bu konulara açıklık
getirmek amacıyla yapılmıştır.
1.3.Araştırmanın Önemi
Belki de dünyadaki en karmaşık ve çelişkili kavramlardan biri entropidir. Ayrıca
bu kavramın yine aynı derece anlaşılması güç olan kendiliğinden olmama veya
tersinirlik ve kendiliğinden olma veya tersinmezlik hususlarına uygulanması ve aynı
zamanda entropinin hal fonksiyonu olarak kabulü ve düzensizlikle eşdeğer olarak
tanımlanmasında da sorunlar mevcuttur. İşte bu araştırma tüm bu hususlara açıklık
getirmek için yapılmıştır.
1.4.Araştırmanın Sınırlılıkları
Araştırmadaki en büyük sınırlılık entropinin genelde kapalı ve hatta izole
sistemler için tanımlanmış olmasına rağmen tüm sistemlere aitmiş gibi gösterilmesi ve
enerjinin arttıkça entropinin artması gerektiği gibi yanlış kavramaların mevcudiyetidir.
Tüm kitaplarda entropinin hal fonksiyonu olması hususu daima Carnot çevrimine göre
anlatılmış ve buna karşılık Clausius kavramına göre entropinin tersinmez olaylarda
2
artması ve tersinir olaylarda değişmemesi hususu göz ardı edilmektedir. Ayrıca entropi
ister tersinir ister tersinmez olsun tüm olaylarda öğrencinin kafasını allak bullak edecek
şekilde daima tersinir bir yol üzerinden hesaplanmaktadır. Entropi hal fonksiyonu
olarak kabul edilmesine rağmen (hal fonksiyonları daima bir fark olarak bulunmakta
mutlak değerleri belirlenememektedir) üçüncü kanuna göre mutlak değerleri
hesaplanmaktadır.
1.5.Varsayımlar
Burada yapılan bir varsayım yoktur. Tezin amacı da zaten entropi konusunda
yapılan varsayımlara açıklık getirmektir.
1.6. Tanımlar
Burada konumuzla ilgili birkaç önemli termodinamik kavramı tanımlamakta
fayda vardır.
1.6.1. Sistem
Belli sınırlar arasında tanımlanmış olan uzay parçasına “sistem” adı verilir.
Sistem katı, sıvı veya gaz halinde olabilir. Sistemin dışında “ortam” bulunur. Sistem ve
ortamı da evren kaplar. Sistemi kabaca üçe ayırmak mümkündür. Sistem sınırları içine
ne ısı ne de madde akışına izin vermiyorsa “izole(adyabatik)”, ısı akışına izin verip
madde akışına izin vermiyorsa “kapalı” her ikisine de izin veriyorsa “açık” olarak
nitelenir.
Şekil 1.1 Sistem ve sistemin tipleri
Termodinamik sistemin mutlak değeri ölçülebilen ve hal değişkeni olarak
tanımladığımız, kütle (m), hacım (v) , sıcaklık (t) ve derişim (c) gibi özellikleri ile
3
ilgilenir. Bu özellikler bir eşitlik ile birbirine bağlanıyorlarsa bağımlı bağlanamıyorlarsa
bağımsız değişken olarak adlandırılır.
Bu özellikle madde miktarı ile değişmiyorsa
veya bir başka deyişle sistemi parçalara ayırdığımızda bir farklılık göstermiyorsa (T,P)
bunlara “intensif ” veya “şiddet”, farklılık gösteriyorsa “ekstensif ” veya “kapasite”
(m,v) özellikleri adı verilir. Kapasite özellikleri toplanabilir. İki tane kapasite özelliğinin
oranı bir şiddet özelliğidir (=m/v). Bir sistemi tanımlamak için vermemiz gereken
minimum şiddet özelliği sayısına o sistemin serbestlik derecesi adı verilir .
Sistem sabit tutulan hal değişkenine göre de çeşitli isimler alır . Örneğin
sıcaklığın sabit tutulduğu sistemler izotermal, hacmin sabit tutulduğu sistemler izokorik,
basınç sabit tutulduğu sistemlere izobarik, ısı akışına izin verilmediği sistemlere
adyabatik ve herhangi bir sınırlama olmayan sistemlere de politropik sistemler adı
verilir.
Ayrıca sistemin özellikleri gidilen yola bağımlı ise hal fonksiyonu ve tam
differensiyel yola bağımlı ise yol fonksiyonu olarak bilinir .
U=U(x,y,z) şeklinde bir fonksiyon ise bunun türevi
U
U
U
dy
dU
dx
dz
x y , z
z x , y
y x , z
(1.1)
Eğer U=U(x,y) şeklinde ise (ki, termodinamik fonksiyonlar genelde bu
formattadır ) yukarıdaki ifade ;
U
U
dy
dU
dx
x y
y x
şeklini alır.
Buda dU=Mdx +Ndy şeklinde yazılabilir.
(1.2)
4
U
M
x y
ve
U
N
y x
(1.3)
şeklinde verilen bir diferansiyelin, tam diferansiyel olma veya U fonksiyonunun hal
fonksiyonu olma şartı
veya
veya
şeklinde verilir
U bir hal fonksiyonu ise
Şekil 1.2 Hal Fonksiyonu Olma Şartı
Eğer U1=U2= U3 =U ise U bir hal fonksiyonudur.
Başka bir deyişle bir hal fonksiyonunun değişimi gidilen yola bağımlı değildir.
Hal fonksiyonunun türevsel haline de tam diferansiyel denir ve d ile gösterilir. Bunun
aksine hal fonksiyonu olmayan fonksiyonlar gidilen yola bağımlıdır. Bunlara da yol
fonksiyonu denir. Bunların türevsel halleri de bundan sonra ile gösterilecektir.
(1.4)
şeklindedir.
Eğer tam diferansiyel değilse çevrim integrali sıfır olmaz
(1.5)
ve
5
(1.6)
Ayrıca bir tam diferansiyelin integrali daima bir fark iken ,tam olmayan
diferansiyel kendine eşittir.
(1.7)
(1.8)
ve
(1.9)
Sistemin özellikleri zaman ile değişmiyorsa sistem dengede demektir. Bunu bir
örnek üzerinde açıklayalım:
Şekil 1.3 Denge şekilleri :(A) yarı-kararlı denge, (B) kararsız denge ve (C) kararlı denge
denge şartı
dU
=0
dr
(1.10)
şeklinde verilir.
Ancak dengenin şeklini bulmak için ikinci türeve bakılmalıdır.
Buna göre:
d2U
≥0(kararlı )
dr 2
şeklinde kabul edilir.
d2U
< 0 (kararsız )
dr 2
(1.11)
6
1.6.2. İş
Eğer bir kuvvetin uygulandığı nokta yer değiştiriyorsa bu durumda bir iş
yapılıyor demektir. Bunu da aşağıdaki şekil ile açıklayabiliriz:
Şekil 1.4 İşin gösterimi
Eğer hareket yönü ile uygulanan kuvvet arasında bir açısı var ise
δw = F cos θdr
(1.12)
bir kuvvetin Kartezyen koordinatları cinsinden olan bileşenleri Fx, Fy ve Fz şeklinde ise
δw = Fx dx + Fydy + Fz dz
(1.13)
olur. Eğer uygulanan kuvvet alınan mesafe boyunca sabit ise
w=
r1
Fdr = F(r
∫
r0
1
- r0 )
(1.14)
şeklini alır .
1kg’lık kütleyi 1 m kaldırmak için yapılması gereken iş
w=mgr1=1kg×9,80655ms-2×1m = 9,80655 kgm2s-2(veya Nm)
olarak bulunur.
1.6.3.Enerji
Enerjinin bugünkü şekilde tanımlanması uzun süre almıştır. 1789’da Thomas
Young enerjiyi “görünür” ve “potansiyel” olmak üzere ikiye ayırmış, daha sonra
Thompson görünür enerjiye” kinetik enerji” adını vermiştir. Bir r0 durumundaki
taneciğe bir f(r ) kuvveti uygulayalım ve bu taneciği r0’dan r1’e getirelim.
Bu durumda yapılan iş
7
r1
t1
r0
t0
w∫
F(r)dr ∫F(r)
1
mv 12
2
1
mv 02
2
t1
t1
t1
v1
dr
dv
dt ∫F(r)vdt ∫mavdt ∫m
vdt m ∫vdv
t0
t0
t0
v0
dt
dt
(1.15)
şeklinde verilir .
v0= 0 ise ve v1 = v dersek
1
E K mv 2
2
(1.16)
Bulunur.
Kuvvet yalnızca mesafenin fonksiyonu olduğunda potansiyel enerji cinsinden
r1
F(r)dr = dU(r) ⇒∫F(r)dr = U(r0 ) U(r1 ) = E K1 E K0
r0
(1.17)
bulunur.
Buradan da görüldüğü üzere potansiyel enerji artarken kinetik enerji azalır. Buda
enerjinin korunumu ilkesinin matematiksel bir ifadesidir. Durağan bir cismin kinetik
enerjisi sıfırdır . Ancak potansiyel enerjinin sıfır olduğu noktayı tanımlamak mümkün
değildir . Yalnızca potansiyel enerjinin farkı tanımlanabilir.
8
2 .KAVRAMSAL ÇERÇEVE
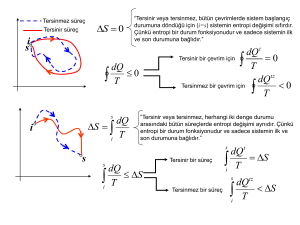
2.1 Tersinirlik ve Tersinmezlik Kavramları
Bu kavramlar en iyi bir örnek üzerinde gösterilebilir
Şekil2.1Tersinir ve tersinmez olaylara bir örnek
Burada görüldüğü üzere eğer sistem tek bir basamakta ve ani olarak değişime
tabi tutulursa sistemdeki denge alt üst olmaktadır. Örneğin sistem birden bire bir
sıkıştırmaya tabi tutulursa pistonun yakınındaki moleküller çok daha hızlı bir şekilde
sıkışıp ısınacağından sistemde bir
sıcaklık farkı meydana gelecektir. Bir sistemde
sıcaklık farkı varsa sistemde dengeden bahsedilemez. Termodinamik bu tip denge dışı
olayları açıklayamaz.
Ancak bu değişimi sonsuz tane basamakta örneğin bir kum tanesi eklemek
suretiyle yaparsak sistemdeki sıcaklık farkıda sonsuz küçük olacağından sistem esas
olarak dengede farz edilebilir. İşte bu duruma tersinir süreç denir.
Termal denge gazın belli bir anda belli bir hacime, sıcaklığa ve basınca sahip
olması demektir. Buna kararlı hal de denmektedir. Termal dengenin olması için en
azından basınç ve sıcaklığın değişmemesi gerekir. Ancak bu durumun meydana gelmesi
9
için sistemin her anlamda sabit olup hareket etmemesi gerekir. Çünkü sistemin bir
halden başka bir hale geçmesi için dengenin bozulması gerekir. İşte bu denge bozulma
miktarı ne kadar uzun ise sistem o kadar tersinmez demektir. Tabiatta kendiliğinden
olan süreçlerin hepsi belli bir hızda ve tersinmez olarak cereyan eder. Termodinamik
süreçlerin
hiçbiri sürekli devam etmez ve sistem dengeye geldiği anda sonlanır.
Sistemin eninde sonunda dengeye gelmesi gerektiğiden buna termal kıyamet adı verilir.
Tersinir süreç ise yarı kararlı süreç olarak bilinir ve biribiri ardından gelen sonsuz
sayıdaki basmaklardan oluşur. Değişim çok ufak olduğundan sistem esas olarak
dengede kabul edilir.
2.2 Termodinamiğin I. Kanunu
Termodinamiğin en önemi kurallarında biri olan I.Kanun enerjinin korunumu
ilkesine dayanır. Buna göre bir cisme q ısısı verir ve ona bir w iş yaparsak iç enerjideki
değişim du= δq+δw veya u = q + w şeklinde tanımlanır. IUPAC kurallarına göre
sisteme verilen ısı ve iş (+), alınanlar ise (-) olarak kabul edilir. Bilindiği gibi iç enerji
bir hal ve iş ve ısı ise bir yol fonksiyonudur. Buna göre du gidilen yola bağlı olmayıp
sadece sistemin başlangıç ve son hallerine bağlıdır. Eğer bu bir hal fonksiyonu
olmasaydı bu durmada farklı yollardan gitmek ve dönmek suretiyle yoktan enerji
yaratılabilir ve termodinamiğin I. Kanunu ihlal edilebilirdi. Başka bir deyişle enerjinin
hal fonksiyonu olması dışardan herhangi bir katkı olmaksızın çalışılabilecek olan birinci
derece devri daim makinasının önündeki tüm yolları kapatmaktadır.
2.3 Termodinamiğin II Kanunun
Bu kanun iki açıdan önemlidir. Bunlardan birincisi dünyada bazı olaylar
kendiliğinden cereyan eder. Örneğin bir gaz mevcut olan tüm hacımı kaplayacak şekilde
kendiliğinden yayılır, sıcak bir cisim ortamın sıcaklığını alacak şekilde kendiliğinden
soğur, kimyasal bir süreç belli bir yönde cereyan eder, iki gaz birbiri ile kendiliğinden
karışır. Ancak bunların aksinin oluştuğu hiç görülmez ve bunu yapmak için mutlaka bir
katkı yapmak gerekir. İşte hangi olayların kendiliğinden olup hangilerini kendiliğinden
olmayacağını tanımlamak II. Kanunun konusudur.
10
Dünyadaki enerji büyük oranda yakıtların içinde olan iç enerji şeklinde
bulunmaktadır. En temel enerji şekli ısıdır . Enerjiyi ısı formunda hiçbir kayıp olmadan
evlerimizi ısıtmakta veya mutfakta yemeklerimizi pişirmekte kullanabiliriz. Ancak bu
ısının tümünü bir tekerleği döndürmek, veya arabamızı çalıştırmak için kullanmak
mümkün değildir. Çünkü bu durumda ısı mekanik enerjiye dönüştürülmelidir. İşte bu
işlemi tam olarak yapmak mümkün değildir. Çünkü işe dönüştürülen ısının büyük bir
kısmını tabiata vergi olarak vermek gerekir. Çekilen ısının işe dönüştürülen veya vergi
kesildikten sonra elimize geçen kesrine makinenin verimi denir. Makineden ne kadar
verim elde edilebileceği işlemin ne oranda tersinir olarak yapılabileceğine bağlıdır.
2.3.1 Maksimum İşin Elde Edilmesi
Aşağıdaki gibi bir sistem düşünelim ve sistem tek bir safhada v1 hacminden v2
hacmine genleşsin ;
Şekil 2.2 Tek basamakta yapılan tersinmez genleşme
(1) (2) genleşmesi ile yapılan iş
w= -mgh (iş ortama yapılıyor)
(2.1)
eğer pistonun alanı a ise pzıt pistonun hareketine mani olan basınçtır ve en yüksek
değeri p2 olabilir
mg=-p2 aw=-p2 a h
(2.2)
ah=v w = -p2v=-p2(v2-v1)
(2.3)
Bunu grafiksel olarak gösterelim;
11
Şekil 2.3 Tek basamakta tersinmez süreçlerde elde edilen işin minimum olması
Şimdi de bu işin iki basamakta yapıldığını düşünelim
Şekil 2.4 İki basmakta elde edilen işin daha yüksek olması
Görüldüğü gibi iki basamaklı genleşmede elde edilen toplam iş tek basamaklı
genleşmede elde edilen toplam işten daha büyüktür. Çok basamaklı genleşmede elde
edilen toplam iş her basamakta elde edilen toplam işlerin toplamıdır.
Tek basamakta elde edilen toplam iş
δw Pzıı dV
(2.4)
İş bir hal fonksiyonu olmadığından
2
1
V2
w w Pzıı dV
(2.5)
V1
Dolayısıyla iki basamaklı genleşmedeki toplam iş
w= wilk basamak +wikinci basamak = -{p’zıt(v’-v1) + p’’zıt(v2-v’)}
(2.6)
Eğer bu genleşme işini sonsuz tane basamakta tersinir olarak yaparsak ( örneğin
içi kum dolu bir torba almak ve her defasında bundan tek bir kum tanesi almak sureti
ile) genleşme sonunda elde edilebilecek olan maksimum iş elde edilir. Bunu grafikte
gösterirsek ;
12
Şekil 2.5 Sonsuz basamaklı (tersinir)genleşmede elde edilen maksimum iş
Burada görüldüğü üzere tam tersinirlik asla mümkün olmadığından asla
maksimum iş elde etmek mümkün değildir. Yani teorik veya termodinamik verimle
gerçek verim asla aynı olmayacaktır.
2.3.2 Carnot Çevrimi ve Isı Makinaları
Enerjinin direkt olarak ısıya döndürmesinde bir sorun yoktur. Bu şekilde elde
edilen enerji ısıl işlemlerde örneğin meskenlerin ısıtılmasında, pişirmede yahut başka
kimyasal veya fiziksel işlemler için kullanılabilir. Fakat bir makinayı çalıştırmak yahut
bir vasıtayı yürütmek veya bir mermiyi fırlatmak için ısı mekanik enerjiye
dönüştürüldüğünde sorunlar başlamaktadır.
Bu hususu ilk inceleyen Fransız bilim adamı adı Carnot'tur. Carnot bunun için
aşağıdaki tersinir çevrimi önermiştir .
Şekil 2.6 Carnot çevrimi
13
Proses (I): izotermal tersinir genleşme
Gaz yüksek bir T2 sıcaklığında v1 haciminden v2 hacimine izotermal ve tersinir
bir şekilde genleşmektedir. Bu sırada sistem tarafından bir q2 ısısı soğurulmaktadır.
1 mol ideal gaz aldığımızda genleşen gazın ortama yaptığı iş:
w I P dV RT2
V
dV
RT2 ln 2
V
V1
V2
V1
ΔUI q I w I 0
q I q 2 w I RT2ln
V2
V1
(2.7)
(2.8)
(2.9)
Proses (II) –adiyabatik tersinir genleşme
Gazın sıcaklığı soğuk kaynağının sıcaklığı olan T1 değerine düşene dek v2
hacminden v3 hacmına genleşir.
qII 0
ΔUII w II CV (T1 T2 )
(2.10)
Proses (III): İzotermal tersinir sıkıştırma
Gaz T1 sıcaklığında V3 haciminden V2 hacimine izotermal ve tersinir bir şekilde
sıkıştırılır. Bu sırada sistem soğuk ısı deposuna
q1 ısısı aktarır.1 mol ideal gaz
tarafından gaz üzerinde yapılan sıkıştırma işi:
w III P dV RT1
V2
V3
V
dV
RT1 ln 2
V
V3
(2.11)
yapılan işlem izotermal olduğuna göre
ΔU III 0
q III q1 w III RT1ln
V2
V3
(2.12)
14
Proses (IV): Adyabatik tersinir sıkıştırma
Gazın sıcaklığı sıcak kaynağının sıcaklığı olan T2 değerine çıkana dek
V2
haciminden V1 hacimine sıkıştırılır.
qIV 0
ΔUIV w IV CV (T2 T1 )
Burada görüldüğü üzere bu çevrim sonunda T2 sıcaklığındaki
(2.13)
sıcak bir ısı
deposundan q2 ısısı alınmış ve t1 sıcaklığındaki soğuk ısı deposuna q1 ısısı aktarılmıştır.
aradaki fark alınan ısının işe çevrilen kısmıdır.
w = q2 - q1
Verim η
Elde edilen iş q 2 q1
q
1 1
Verilen ısı
q2
q2
(2.14)
ii ve iv prosesleri işleri birbirini götüreceğinden,
w net=w I +w III
RT2ln
V2
V
RT1ln 2
V1
V3
(2.15)
adyabatik proseslerde
CV
CV
V2 V3
CV
CV
V2 V1
T2 R V2 T1 R V3
T2 R V1 T1 R V2
(2.16)
yazılabilir. bu iki ifadeyi birbirlerine bölersek
V2 V3
V1 V2
buradan
w net RT2ln
V2
V
V
V
RT1ln 2 RT2ln 2 RT1ln 2
V1
V3
V1
V1
w net R(T2 T1 )ln
V2
V1
(2.17)
15
Gaz tarafından soğurulan toplam ısı
q net w net q 2 q1
V2
V
RT1ln 2
V1
V3
V
V
RT2ln 2 RT1ln 2
V1
V3
q net w net RT2ln
V2 V3
V1 V2
olduğundan
q net w net RT2ln
V2
V
V
V
RT1ln 2 RT2ln 2 RT1ln 2
V1
V3
V1
V1
q net w net R(T2 T1 )ln
η
w net
q2
R(T2 T1 )ln
RT2ln
V2
V1
V2
V1
V2
V1
T2 T1
T
1 1
T2
T2
Önce böyle bir makinayı şematik olarak gösterelim :
Şekil 2.7 Carnot makinasının şematik gösterimi
Bu tip makinanın en önemli özelliği onun verimidir.
η
w
q2
(2.18)
16
w w q 2 q1
η
w
q
T
1 1 1 1
q2
q2
T2
(2.19)
Buradan da görüldüğü gibi sıcak ısı deposundan alınan bir q2 ısısının tamamını
işe
döndürecek
bir
makine
yapılamaz.
Bunu
yapmanın
imkânsızlığı,
bize
termodinamiğin ikinci kanunu olarak bilinen tabiatın temel kanunlarından birini getirir.
2.4. Entropi Kavramı
Dünyada bazı olaylar kendiliğinden cereyan eder. Örneğin bir gaz mevcut olan
tüm hacımı kaplayacak şekilde kendiliğinden yayılır, sıcak bir cisim ortamın sıcaklığını
alacak şekilde kendiliğinden soğur, kimyasal bir süreç belli bir yönde cereyan eder ki
gaz birbiri ile kendiliğinden karışır. Ancak bunların aksinin oluştuğu hiç görülmez ve
bunu yapmak için mutlaka bir katkı yapmak gerekir. Dolayısıyla kendiliğinden olan
olayları tanımlayacak bir özellik olmalıdır.
Önce bu tip bir olayın cereyan ettiği aşağıdaki gibi bir sistem düşünelim
Şekil 2.8 Termodinamikte göz önüne alınan sistem
Peki, olayların kendiliğinden cereyan etmesini ne belirler? Bu izole sistemin
enerjisi olamaz çünkü I. kanuna göre enerji korunur ve izole bir sistemin enerjisi sabit
olur.
Belki de bu incelenen sistemin enerjisidir. Ancak bunun da olamayacağını
gösteren bir kanıt vardır. İdeal bir gaz kendiliğinden vakuma dolar ve bu sırada sistemin
iç enerjisi değişmez.
17
Zıplayan bir top alalım. Bunun kinetik enerjisi sürtünme yolu ile ısı enerjisine
dönüşür ve yerde durağan bir hale gelir. Oluşan ısı enerjisi de sonsuz büyüklükteki yer
alanının moleküllerinin termal enerjisini artırmakta kullanılır.
Ancak sıcak bir yüzey üzerindeki bir topun kendiliğinden zıplamaya başlaması
asla görülmez. Bunun için son derece özel şartların yerine getirilmesi gerekir. Birincisi
yüzeydeki termal hareket topta yoğunlaşmalıdır. Ayrıca topu yukarı doğru hareket
ettirmek için tüm moleküller yukarı doğru hareket etmelidir.
Ancak bilindiği gibi
termal hareket gelişigüzel bir harekettir ve yukarda bahsedilen şartların oluşma olasılığı
hemen hemen sıfırdır.
Termodinamiğin II. Kanunu fizik, kimya ve mühendislik açısından son derece
önemlidir. Kimyacı açısından en önemli yanı kimyasal reaksiyonların olup
olmayacağını ve ne ölçüde olacağını göstermesidir. dolayısıyla kendiliğinden meydana
gelen olayları kavramak büyük önem taşımaktadır.
Kendiliğinden olan olaylara birçok örnek verilebilir. Örneğin bir ucu ısıtılan bir
çubukta ısı kendiliğinden çubuk boyunca yayılır. Ancak bunun aksi asla söz konusu
değildir. Yani sıcaklığı her tarafta aynı olan bir metal çubuğun bir ucu kendiliğinden
ısınırken diğer ucu da kendiliğinden soğumaz. Bunu yapmak için ısının çubuğun bir
ucundan bir ısı makinası ile alınıp eşdeğer işe çevrildikten sonra diğer ucuna verilmesi
gerekir.
Bu olayı bir örnek ile açalım: Kütleleri aynı olan biri 00C diğeri de 1000C’de
olan iki bakır blok alalım. Bunları adyabatik olarak yalıtılmış bir ortamda birbiri ile
temasa getirelim termodinamiğin I.Kanununa göre üç tane olasılık vardır:
Şekil 2.9 Termodinamiğin 1. ve 2. kanununa göre olan olasıklıklar
18
Deneyimler (1) prosesinin asla kendi başına mümkün olmadığını göstermektedir.
Yani soğuk bir cisim kendiliğinden daha da soğurken sıcak bir cisim daha ısınmaz. (2)
prosesi ise bloklar termal dengeye erişmeden evvel birbirlerinden ayrılmaları
durumudur. (3) prosesi de blokların uzun bir süre temasta tutulmaları sonunda termal
dengeye gelmeleri durumudur.
Şimdide bu proseslerin terslerini göz önüne alalım. (1) prosesinin tersi
kendiliğinden olurken (2) ve (3) proseslerinin tersleri asla kendiliğinden olmaz.
Acaba bir dış katkı vasıtası ile örneğin (3) prosesini tersine döndürmek mümkün
müdür? Bildiğimiz 500C sıcaklıkta bulunan kütleleri aynı olan iki metal bloğun termal
olarak yalıtılmış olan bir ortamda temasa getirilmesi durumunda birinin sıcaklığı
600C’ye çıkarken diğerinin sıcaklığı 400C’ ye inmez. Acaba bir dış katkı ile bu proses
gerçekleştirilemez mi?
Bunun için 500C sıcaklıkta bulunan kütleleri aynı adyabatik olarak izole edilmiş
silindirlerde bulunan iki ideal gaz ile yine aynı şekilde izole edilmiş olan kütleleri aynı
olan iki tane bakır blok alalım ve aşağıdaki prosesi gerçekleştirelim.
Şekil 2.10 Kentliğinden olmayan tersinir bir prosesi dış bir katkı ile tersine çevirmek
Buradan görüldüğü üzere bloklardan birinin sıcaklığı 600C’ye çıkarken
diğerininki 400C’ye inmiştir. Gazları tekrar eski haline döndürmek için bir iş yapmak
gerekir ki bu da bize Clausius prensibini getirir.
Bu prensibe göre “soğuk bir depodan sıcak bir depoya ısı aktarımı dışında başka
bir etki oluşturmadan çalışan dönüşümlü bir makina yapmak mümkün değildir”.
19
Görüldüğü
üzere
ısının
kendiliğinden
yayılma
prensibinin
tersine
döndürülmesinde termodinamiğin I. kanunu açısından bir sakınca yoktur. Ancak
buradaki tüm sorun sistemin bazı kısımlarında ve çevresinde bir değişiklik yapmaksızın
ısının eşdeğer miktarda işe döndürülememesidir.
II. Kanunu ilk olarak Lord Kelvin tanımlamıştır. Buna göre “sıcak bir ısı
deposundan ısı alıp onun bir kısmını soğuk bir ısı deposuna aktarmadan tamamını
eşdeğer işe döndürmek mümkün değildir” alınan ısının işe döndürülen bu kısmına
makinanın verimi adı verilir. bu tanıma göre verimi %100 olan bir makina yapılamaz.
Kısacası tabiatta kendiliğinden cereyan eden olaylar tersinmez bir şekilde olur.
Zaten I.Kanundan bildiğimiz üzere tersinir olaylar sonsuz uzun bir süreç alır. Tüm bu
yukarıda söylediklerimizden şu sonuç çıkmaktadır: “Kendiliğinden yürüyen olayları
herhangi bir dış katkı olmaksızın tersine döndürmek mümkün değildir". Buda
termodinamiğin II. Kanununun bir başka şekilde ifade edilmesidir.
Kendiliğinden yürüyen olayların (örneğin yukarıdaki a b proseslerinin)
termodinamik açıdan tersinmez olduklarını belirledikten sonra sıra bu kendiliğinden
olma prensibini açıklayan bir fonksiyonun tanımlanmasına geldi bu fonksiyona entropi
adı verilir ve S ile simgelenir. Entropi tanım olarak
dS
qter
(2.20)
T
şeklinde verilir.
Önce ortamın entropi değişimi dS’yi tanımlayalım. Ortamı t sıcaklığında büyük
bir ısı deposu olarak tanımlayalım. Bu depoya ısıyı işe çeviren bir makina ve bu
makinaya da bir ağırlık bağlayalım ağırlık düşünce depoya bir q ısısı aktarılır. Depoya
ne kadar fazla ısı aktarılırsa depo içinde olan termal harekette o kadar fazla olur. Bu
durumda yaratılan entropi de o denli yüksektir. Bunun yanında ısıyı sıcak bir ısı deposu
yerine daha soğuk bir depoya aktarırsak (yani soğuk depodan daha soğuk bir depoya )
yaratılan entropi de o kadar düşük olur. Buradan;
dS '
q'
T
S '
qter
T
şeklinde verilir.
Adyabatik olaylarda
(2.21)
20
q = 0 ve S=0
(2.22)
İzobarik olaylarda
S
H
T
(2.23)
İzotermal olaylarda
S
U
T
(2.24)
İlgilenilen değişim olduğu zaman sistem entropisindeki değişim dS olsun (bizde
bunu belirlemek istiyoruz). Bu iki hali birbirine bağlayan bir yol bulalım. Örneğin
sistemi izotermal tersinir olarak genleştirdikten sonra yine izotermal ve tersinir olarak
sıkıştıralım. S bir hal fonksiyonu olduğundan (ki bunu tüm tartışma da buradan
çıkmakladır) dS her iki yolda da aynıdır. Sistemin tersinir olarak sıkıştırılmasındaki
entropi değişimi -dS verilmesi gereken ısıda -qter olur. Bu enerji çevreden gelme
zorunda olduğundan -q′=qter
ve ds′=qter/t olur. Sistem tersinir bir çevrime tabi
tutulduğundan;
q ter
0
T
q
dS ter
T
dS
(2.25)
şeklinde bulunur.
Şimdide tersinmez bir sistem alalım. Sistem ile ortamın termal dengede olmasını
sağlayalım (bunların mekanik dengede olmaları şart değildir). Örneğin bir gaz
çevresinden daha yüksek basınca sahip olabilir bu durumda herhangi bir değişim
sistemin entropisinde ds, ortamın entropisinde de ds′ değişimine sebep olur sistem
tersinmez bir değişime tabi tutulursa toplam entropide değişimi sıfırdan daha büyük
olur. ds+ds′ 0 veya ds -ds′ olur .
dS
idi
qter
T
(2.26)
21
qter= sisteme verilen ısı
buradan
dS
q
(2.27)
T
bulunur. Bu ifade Clausius Eşitsizliği olarak bilinir.
Buradan iki sonuç çıkar:
Tersinir olaylarda toplam entropi sıfır olup tersinmez olaylarda ise toplam
entropi>0 olur. Peki, hani entropi hal fonksiyonuydu ve gidilen yola bağlı değildi!
2.4.1Entropinin Fiziksel Anlamı
Kendiliğinden olan bütün olaylarda sistemin düzensizliği artar. Örneğin bir
gazın başka bir gaz içine difüzlenmesi, gazın boşlukta genleşmesi gibi kendiliğinden
olan olayların hepsinde düzensizlikte büyük bir artış görülür. Bu olayların hepsinde
entropide arttığına göre entropi sistemde meydana gelen düzensizlik artışının bir ölçütü
olarak düşünülmelidir. Kısaca istemli veya kendiliğinden olan bir hareket daha fazla
düzensizlik oluşturacak şekilde cereyan eder. Ancak entropinin düzensizliğe
bağlanmasında da büyük sorunlar vardır.
Faz değişimlerinde düzensizlik dolayısıyla entropi katı sıvı gaz şeklinde
değişir. katılarda düzenli bir örgü yapısı varken sıvılarda bu yapı bozulur. Buharlaşma
ise düzensizliğin en yüksek seviyeye çıktığı haldir. Dolayısıyla sıcaklık ile entropi
arasında doğrusal bir ilişki vardır. Mutlak sıcaklıkta daha sonra göreceğimiz gibi entropi
sıfıra yaklaşır. Düzensiz hal olasılığı düzenli hal olasılığından çok daha yüksektir. İlk
olarak 1896 yılında Boltzmann mutlak entropiyi,
S k ln w sabit
(2.28)
şeklinde tanımlamıştır. Burada k Boltzmann sabitini w ise termodinamik olasılığı
göstermektedir. Daha sonra Planck bu sabit terimin sıfıra eşit olduğunu kanıtlamıştır.
Düzenli halde w=1 ve S=0 olur.
22
Şimdide kendiliğinden olan bazı olaylarda olan entropi değişimlerine bakalım
(İ) Tersinmez adyabatik genleşme
q=0
(2.29)
dssis + dsort (Clausius eşitsizliği )
(2.30)
dSort
qter
T
0
(2.31)
olursa
dssis>0 olur .
(2.32)
(ii)Tersinmez izotermal genleşme
ideal gazlarda
U
0
T V
(2.33)
dU q w 0
q w
(2.34)
Eğer gaz izotermal olarak vakuma karşı genleşiyorsa (p=0) ortama ne ısı yayılır
nede bir iş yapılır. ( q=0 ve w=0 ) dolayısıyla ortamın entropisi değişmez.
Ancak sistem v1v2 genleşmesi yaptığından sistemde
ΔS nRln
V2
V1
(2.35)
kadarlık bir entropi değişimi olur. Dolayısıyla dssis > 0 olur .
Şimdide ortamın entropisine bakalım: Her iki durumda da (yani adyabatik
tersinmez genleşme ve vakuma karşı izotermal genleşme) q=0 olduğundan dsort=0
olur.
dstop = dssis + dsort dstop = dssis
(2.36)
veya
dstop > 0
(2.37)
23
kısaca tersinmez olaylarda toplam entropi artar.
Şimdide genleşme işini sonsuz küçük basamaklar halinde yani tersinir olarak
yapalım. Bu durumda sistem ortamdan q kadar ısı çeker ve entropi artışı q/t olur.
Ortamdan çekilen ısı –q olduğuna göre entropide azalma –q/t olur. Dolayısıyla tersinir
proseslerde
Stop
q q
0
T T
(2.38)
demek ki tersinir olaylarda toplam entropi değişimi sıfırdır. Kısaca olayın
kendiliğinden olması için sistemin entropisi dolayısıyla toplam entropinin artması
gerekir dssis > 0 olur.
İdeal gazlarda
dU q w nCV dT q PdV
q ter nCV dT PdV nCV dT nRT
dV
V
dolayısıyla;
q ter
dT
dV
nCV
nR
T
T
V
buradan
dS
S S2 S1 nCV ln
T2
V
nR ln 2
T1
V1
(2.39)
dolayısıyla ideal gazlarda entropi değişimi sıcaklık ve hacımın fonksiyonundur.
V2 T2 P1
V1 T1P2
olduğundan;
S nCV ln
T2
T
P
nR ln 2 nR ln 2
T1
T1
P1
ΔS nCV R ln
T2
P2
T2
P
nRln 2 ΔS nCP ln nRln
T1
P1
T1
P1
(2.40)
24
izotermal olaylarda T1=T2
ΔST nRln
P2
V
nRln 2
P1
V1
(2.41)
izobarik olaylarda p1= p2
ΔSP = nC P ln
dSP =
T2 q P ΔH
=
=
T1
T
T
δq P dH
=
T
T
(2.42)
izokorik olaylarda V1= V
ΔSV nC V ln
dSV
T2 q V ΔU
T1
T
T
δq V dU
T
T
(2.43)
dolayısıyla sabit basınç altındaki entropi değişimi grafiksel olarak kolaylıkla
bulunabilir.
v
Şekil 2.11 Entropinin grafiksel olarak bulunması
Bu yöntem özellikle katı ve sıvılar için uygundur. Çünkü bunlarda Cp genellikle
sıcaklığın karmaşık bir fonksiyonudur.
25
2.4.2 Entropinin Bir Hal Fonksiyonu Olması
Bilindiği gibi hal fonksiyonlarında çevrim integrali sıfır idi. Carnot çevrimindeki
entropi değişimini hesaplayalım.
I.İzotermal tersinir genleşme
ΔS I
q I
Rln
T2
V2
V1
(2.44)
II. Adyabatik tersinir genleşme
(2.45)
ΔSII 0
III. İzotermal tersinir sıkıştırma
ΔSIII
q III
T1
q1
V
Rln 2
T1
V3
(2.46)
IV. Adyabatik tersinir sıkıştırma
ΔSIII 0
Buradan toplam entropi sıfır olur.
Bunların P-V ve T-S eğrilerine bakarsak;
Şekil 2.12 Carnot çevriminde P-V ve T-S değişimleri
(2.47)
26
Entropinin hal fonksiyonu olduğu genelde yukardaki gibi Carnot çevrimine
dayandırılmaktadır.
2.4.3 Entropinin bir hal fonksiyonu olduğunun ispatı
Aşağıdaki gibi bir çevrim alalım
S1a b Sa2b Sçevrim
ΔScevrim ΔS1a b ΔSa2b
(2.48)
Bunu biraz daha açalım. Birçok ufak Carnot çevriminden oluşan bir toplam
proses alalım;
Şekil 2.13 Entropinin hal fonksiyon olduğunun ispatı
Bu prosesleri hepsini yapınca toplam proses de yapılmış olur.
w T2 T1
q2
T2
w q 2 q1
q 2 q1 T2 T1
q2
T2
T2 q 2 q1 q 2 T2 T1
27
Bunu açarsak;
q1T2 q 2T1
q1 q 2
q q
2 1 0 S
T1 T2
T2 T1
(2.49)
Bu da entropinin bir hal fonksiyonu olduğunu gösterir.
Tüm çevrimler için
q ter
0
T
(2.50)
Alternatif Yöntem
Şekil 2.14 Entropinin hal fonksiyonu göstermede alternatif yöntem
Burada bc ile da birbirlerine ne kadar yaklaştırılırsa abcda alanı
afghe alanı da birbirlerine o kadar yaklaşır.
ab boyunca yapılan iş w
ef boyunca yapılan iş w
limit durumda abef olacağından
w w
(2.51)
ab prosesi izotermal bir proses olduğundan uab =0
w = q2
(2.51) ifadesine göre ;
-w= -w = q2 = q2
(2.52)
28
Aynı şekilde net çevrimin alt kısmı için
q1= q1
Limit durumunda toplam proses bir seri çevrim ile gösterilebilir.
q ter
q
ter 0
T
T
(2.53)
Bu da entropinin bir hal fonksiyonu olduğunu gösterir. Tabi bu birçok açıdan
doğrudur ortada bir çevrim vardır ve bunun sonunda da entropi sıfır çıkmaktadır.
Ancak hal fonksiyonu olmanın bir başka şarttı da gidilen yola bağlı olmamaktır
ki Clausius eşitsizliği bununla büyük bir çelişki içindedir. Bir fonksiyon tersinir ve
tersinmez yollarda fark ederse nasıl hal fonksiyonu sayılabilir? İşte bu noktada işler
içinden çıkılmaz hal almaktadır.
2.5 Clausius Eşitsizliği
Clausius tersinmez sistemlerde
dSSis
q ter
T
(2.54)
ve tersinir sistemlerde de
SSis
q ter
T
(2.55)
olduğunu bulmuştur.
Bu prensibi
SSis
q ter
T
(2.56)
şeklinde açıklamıştır.
Buna göre tersinmez sistemlerde sistemin dolayısıyla evrenin entropisi artar iken
tersinir sistemlerde değişmez.
29
2.6 Minimum enerji prensibi
Adyabatik olarak yalıtılmış bir ortamda bulunan mükemmel bir jeneratörün
ucuna sürtünmesiz bir ipe asılmış olan bir ağırlık bağlayalım. Ağırlık yere doğru indikçe
jeneratörü döndürür ve elektrik enerjisi elde edilir.
Şekil 2.15 Minimum enerji prensibi
Burada görüldüğü üzere mekanik enerji elektrik enerjisine döndürülmektedir.
sürtünmesiz ve adyabatik bir sistem göz önüne aldığımıza göre;
qter =0 Ssis= 0, Sort= 0 ve Stop= 0
Burada bir çelişki varmış gibi görülmektedir. Olay kendiliğinden
cereyan
etmesine rağmen entropi değişimi sıfır olarak bulunmaktadır. Ancak bu kriter sabit
enerjili sistemler için geçerlidir. Buradan şu sonuç çıkar: enerji sabit iken entropi
maksimuma giderken, entropi sabit iken enerji minimuma gider.
2.7 Entropinin Artması (Korunumsuzluğu) Prensibi
Bütün doğal süreçlerde veya termodinamik olarak tersinmez süreçlerde (örneğin
yüksek sıcaklıktaki bir ısı deposunda düşük sıcaklıktaki ısı deposunu ısının
kendiliğinden akması gibi) entropi artar. Doğal olamayan tersinir süreçlerde ise
dışarıdan mutlaka katkı yapılması gerekmektedir. Bu husus yukarda detaylı bir şekilde
anlatılmıştır. Bir başka hususta ısının daha farklı kullanılabilir bir enerjiye
dönüştürülmesi durumunda tamamının bu dönüşüme iştirak etmemsin veya heba
edilmesidir. Başka bir şekilde tabiat mümkün olan en kısa yolu kullanır ki bu yüzden
entropi enerji gibi korunumlu değildir.
30
2.7.1 Entropi ve “Düzensizlik”
Entropi, en genel şekilde sistemin “düzensizliği” şeklinde kabul edilir. Ancak bu
tanım entropi ile ilgili büyük bir kavram kargaşası yaratmaktadır. Bunlardan bazılarını
listelersek
i)Entropik düzensizlik ve görsel düzensizlik: Entropik düzensizlik bazen
görsel düzensizlik sonucu çıkarılmaktadır. Bir oda kendi başına bırakılırsa doğanın
gereği düzensiz olur. Ancak odanın bir başka canlı tarafından düzenlenmesi entropi ile
açıklanamaz.
ii)Entropik Düzensizlik ve Kaos: Entropik düzensizlik bazen de“karmaşa,
kargaşa, belirsizlik” anlamındaki kaos ile karıştırılmaktadır. Hâlbuki kendiliğinden olan
olaylar kaostan düzene göre gider.
iii)Fiziksel Anlamda Entropik Düzensizlik: Fiziksel anlamdaki düzensizlik,
yâni entropik düzensizlik, kısaca, birbirini bütünleyen şu iki şekilde tanımlanabilir:
a: Belirli bir sistemin toplam enerjisinin mevcut tanecikler arasındaki dağılımı;
b: Bir termal işlemde, bir sisteme giren enerjinin tamamının faydalı mekanik işe
dönüştürülememesi sonucunda, sistemin kendiliğinden eski hâline geri dönememesi.
Düzensizlikten kasıt sistemin bu şekilde kendiliğinden geriye dönememesi,
geriye dönebilmek için bir dış müdahalenin şart olması ve sistemin bir önceki haline
göre kendini toparlamasının çok daha zor olmasıdır. Bu olay zamanın geri
döndürülmesi ile de yakından ilişkilidir. Bunu açıklamak için zaman oku kavramı
geliştirilmiştir. Zaman oku, zamanın tek yönde ve sabit bir hızda ilerleyen bir karaktere
sahip olduğu fikrine dayanmaktadır. Buna göre zaman, sâdece bir istikamette ilerler ve
hızı da sabittir. Diğer yandan zaman, süreçlerin bir ifadesi olduğuna göre, hiçbir fiziksel
süreç geriye döndürülemez.
iv)Kozmolojik zaman oku, kâinatın sürekli olarak genişleyeceğini ileri
sürmektedir; buna göre, durmadan genişleyen kâinat da çok uzun zamanlar sonunda
parçaçıklar arasındaki mesafe o kadar büyüyecektir ki sonuçta hiçbir fiziksel süreç
gerçekleşemeyecektir.
31
v)Termodinamik zaman oku ise, farklı ısı kaynakları arasındaki ısı transferinin
ancak ve yalnız daha yüksek sıcaklıktaki ortamdan (sıcak depo) daha alçak sıcaklıktaki
ortama yapılabileceği gerçeğinden hareketle, bunun geriye döndürülemezliğini ifade
etmektedir.
Termodinamiğin her iki yasası kısa bir cümlede özetlenebilir: Evrenin toplam
enerjisi sabit olmasına rağmen entropi sürekli artar. Enerjinin yaratılması veya yok
edilmesi mümkün olmamasına rağmen bir formdan bir başka forma dönüştürmek
mümkündür. Ancak eldeki enerjiyi tamamen kullanılabilir bir işe dönüştürmek mümkün
değildir. Tabi I.Kanuna göre bu işi yapmakta bir sıkıntı yoktur ama II. Kanun tabiatın
vergi memuru gibi yakamıza yapışır ve bunun vergisini tahsil eder ve aldığı vergide
bayağı yüksek bir orandır. İşte bunu açıklayan terim entropidir.
Entropi terimi ilk olarak Boltzmann tarafından kullanılmıştır. Ona göre evrene
“başlangıçta” belirli bir miktar enerji ve madde verilmiş ve bunların bir şekle
döndürülmesine izin verilmiş (tabi yasalar çerçevesinde), fakat yok edilmelerine de
yeniden yaratılmalarına da izin verilmemiştir”.
Boltzmann kaos kavramını bilim dünyasında kullanan ilk kişidir. Boltzmann
matematik çözümlemesi sonunda daha önceden Makswell tarafından hiçbir kuralın
olmadığı her şeyin mutlak rasgeleli içinde yürüdüğü bir sistemde elde edilen dağılım
eğrisini bulmuştur. Maxwell dağılımı kargaşanın mutlak anlamda egemen olduğu
ortamların düzenidir.
vı)Fiziksel anlamda Kaos: Kaos kelimesinin fiziksel anlamı, sözlük
anlamından ve geleneksel anlamından hayli farklıdır. başlangıç olarak, kaosu “sürekli
kararsızlık” ve/veya “belirlenemezlik” olarak tarif edebiliriz.
vıı)Heisenberg’in belirsizlik ilkesi: Modern fiziğin en önemli kavramlarından
biri olan belirsizlik ilkesi, kısaca hareket halinde bulunan bir cismin momentum ve
konumunun aynı anda ve aynı kesinlikle tespit edilemeyeceği esasına dayanır ve
matematiksel olarak δx.δp ≥ h
bağıntısı ile ifade edilir. Burada δx “konum’un
belirlenmesindeki hata”, δp “momentum’un belirlenmesindeki hata” ve h ise, bilinen
32
“Planck katsayısı”dır (6.63x10-34 J.s) hata teorisi’ne göre, momentum [p=m.v] ve
konum [x] ölçümünde bir hata yapmak kaçınılmazdır; bu husus, evren’in kanunlarından
birisidir. Buna göre cismin konum ve momentumunun (dolayısıyla da hız ve kütlesinin)
ölçümündeki hatalardan birisi küçültüldüğü takdirde diğeri büyüyecektir; meselâ
momentum’un ölçüm hatası azaltılarak sıfıra, yâni “tam belirlenebilme” sınırına
yaklaştıkça konum’un ölçüm hatası da sonsuza, yâni “hiç belirlenememe ” sınırına
doğru yaklaşır ve limit hâlde δx = 0 için δp = ∞ olur ki bu, şu demektir:
Eğer cismin momentumunu, yâni hızını ve kütlesini “tam olarak”, yâni sıfır hatâ
ile ölçmüş isek, konumunu, yâni, nerede olduğunu asla bilemeyiz. Ölçümünü“burada”
yaptığımız cisim, evren’in herhangi bir yerinde bulunuyor olabilir. Buradaki
belirsizliğin minimuma indirmek içi ölçümün sonsuz sayıda basamakta yapılması
gerekir ki bu da mümkün değilimdir. İşte kaos olaraktan tanımlanabilen bu belirsizlik
durumu sistemin başlangıç haline son derece bağımlı olduğundan “dinamik kararsızlık”
durumuna karşılık gelir.
vııı) Serbest Genleşmede Entropi Değişimi: İzole bir sistemde bulunan bir
gazın vakuma doğru genleşmesi durumunda ilk ve son hacımlar Vi ve Vs ise genleşme
sonunda Vs> Vi olur. Genleşen gaz tekrar kendiliğinden eski, haline dönemeyeceği için
işlem ‘tersinmezdir. Ayrıca, gazın bu genleşmesi bir “ani genleşme” olduğu için yarı
kararlı da değildir. Gaz tarafından boşluğa karşı yapılan iş sıfırdır (w=0)ve sistem izole
edilmiş olduğu için ısı transferi yoktur (q=0); yâni işlem bir adyabatik bir işlemdir. q=0
olduğundan δS=0 olacağı düşünülebilir ise de bu doğru değildir çünkü sistemin
düzensizliği artmaktadır. δs ’in hesaplanabilmesi için ilk ve son durumlar birbirine bir
tersinir yol ile bağlanırlar. Bu yol bir izotermal genleşmedir. İzotermal genleşme,
serbest genleşme ’den farklı olmasına rağmen aralarında çok mühim bir ortak nokta
vardır: Her ikisinin ilk ve son durumları sabit sıcaklıkta oluşan birer denge durumudur.
(izotermal genleşmede ara sıcaklıklar bilindiği halde serbest genleşmede bilinemez;
ancak bu vaziyet, ilk ve son denge durumları bakımından benzer olmalarını
engellemez.)
Bu hususta en önemli çalışmayı Carnot yapmıştır. Carnot ideal verimi sadece
sıcak ve soğuk depoların ısısına bağlı olduğunu belirlemiştir.
33
Termodinamik kanunlarına göre her cisim hareket etmek ve bunun içinde belli
bir enerji kullanmak zorundadır. Ancak daha öncede söylenildiği her hareket sonlanmak
zorundadır çünkü termodinamiğin I.Kanunun devri daim hareketinin mümkün
olmadığında dolayı belli bir sure sonra durmak zorundadır.
Fakat termodinamik kanunlarının keşfedilmesinin çok öncelerinden başlayarak
günümüze gelinceye dek, birçok hayalperest bu kanunlardan habersiz olarak veya
onlara meydan okuyarak, sürekli bir enerji girdisi olmaksızın çalışarak daimî hareket
(Lat. perpetuum mobile, ing. perpetual motion) ilelebet faydalı iş üretecek makinalar
tasavvur etmişlerdir ve etmeye de devam etmektedirler. Ancak bu kanunların
çiğnenemeyeceği artık herkes tarafından kabul edilmektedir.
34
3. YÖNTEM
3.1 Araştırma Modeli
Bu araştırma bir literatür taraması (survey) niteliğindedir. Entropi ile ilgili tüm
literatür taranmış termodinamik ve fizikokimya kitaplarındaki tanımlar birbirleri ile
karşılaştırmalı olarak incelenmiştir.
3.2 Evren ve Örneklem
Araştırmanın evrenini dünyada bu konu ile ilgili yazılmış tüm termodinamik,
fizikokimya kitapları ve entropi ile ilgili yazılmış makaleler teşkil etmektedir. Örneklem
ise bu konu ile ilgili yazılmış olan fizikokimya kitaplarıdır.
3.3 Veri Toplama Teknikleri
Tüm dünyada bu konuda yapılmış yayınlar araştırılmış ve daha sonrada çeşitli
kitaplar taranmış ve entropi ile ilgili kavramlar karşılaştırmalı olarak incelenmiştir.
3.4 Verilerin analizi
Konu çok karmaşık olduğu için ön test son test modellemesine gidilmemiş ve
elde edilen veriler çerçevesinde yani savlar önerilmiştir.Entropinin hal fonksiyonu olup
olmaması, tersinirlik ve tersinmezlik kavramları detaylı bir şekilde tartışılmıştır.
35
4.BULGULAR VE YORUMLAR
Entropi
kavramının temel teşkil ettiği termodinamiğin ikinci kanunu
hangi tür proseslerin kendiliğinden gerçekleşeceğini belirlemeye çalışır
(Lechner, 1999). İkinci kanun entropiye dayalı olarak, kendiliğinden yüreyen
bir değişim sırasında izole bir sistemin entropisi artar şeklinde açıklanır
(Atkins, 1998). Bu konudaki önemli yanılgılar, sistemin şartlarının göz ardı
edilmesiyle ve genel olarak toplam entropinin (çevre ve sistemin toplam
entropi) yerine sistemin entropisinin dikkate alınmasıyla ortaya çıkar.
Entropinin mikro düzeyde tartışılmasından ziyade düzensizliğin bir ölçütü
olarak gösterilmesi ve sistemlerin maksimum düzensizlik eğiliminde
olduğunun söylenilmesi
öğrencilerde büyük kavram yanılgılarına sebep
olmaktadır. Bunlardan bazıları :
Entropi sistemdeki düzensizliğin sebebidir (Sözbilir, 2001),
Entropi sistemin düzensizliğine eşittir (Sözbilir, 2001),
Entropi arttığı zaman sıcaklıkta artar (Sözbilir, 2001),
İkinci kanuna göre kendiliğinden gerçekleşen olaylarda sistemin entropisi
artmalıdır (Thomasve Schwenz, 1998),
Entropi sistem özerine iş yapıldığını gösterir (Selepe ve Bradley,
1997),
Mikro hal küçük bir haldir. Entropiyle ilişkili değildir (Sözbilir,
2001),
Evrenin entropisi değişmez ya da azalır (Sözbilir, 2001),
Bir sistem her zaman maksimum entropili hale gider (Sözbilir, 2001),
Bir reaksiyonun entropi değişimi her zaman pozitiftir (Sözbilir, 2001).
4.1Entropiye moleküler yaklaşım ve istatistiksel termodinamik
Öncede anlattığımız üzere Boltzmann dağılımı dikkate alınarak mikro
hallerin sayısı ve istatistiksel yorumlan dayalı olarak açıklanabilir. Boltzmann
formülü;
36
S=kblnW,
S=kbln(W2/W1)
Denklemdeki W “termodinamik olasılığı” ifade eder. Termodinamik olasılık
sıcaklık, basınç, hacim, her bir bileşenin mol sayısıyla belirlenmiş termodinamik bir
hal olan özel bir makro hale karşılık gelen mikro hallerin sayıdır (Maes and Redig,
2000).
Mikro hal ifadesiyle; özel bir sistemdeki her bir taneciğin(atom ya da
molekül) konum ve momentumlarını belirterek açıklayan - hal kastedilmektedir.
Mikro hallere bağlı olarak makro durum ve olaylardan bahsedilebilir. Bu bahis aynı
zamanda makro durumun gözlenebilmesini, destekleyen mikro hallerin sayısına bağlı
olarak genişletilebilir. Bu nedenle bir olayı ya da durumu sağlayan mikro hallerin sayısı
ne kadar fazla ise o durumun gerçekleşme ihtimali o kadar fazladır denilebilir
(www.entropysite.com).
Moore(1972) entropinin hal fonksiyonu olma durumunu Carnot çevrimine
dayandırmıştır. Ayrıca entropinin her durmada tersinir bir yol üzerinden hesaplandığını
söylemiş ve entropinin sadece iki denge durum arasındaki fark için tanımladığını
söylemiştir.
Levine (1988)’de kapalı bir sistemin Carnot çevrimini vermesi durumunda
dq
ter/T
değerinin sıfır olduğunu söyler. Levine'e göre sonsuz küçük Carnot çevrimine
bölünebilecek genel çevrim vermiş ve bu çevrimine dayanmakta S=qter/T = 0 olarak
kabul etmiştir. Dolayısıyla entropi fonksiyonu kapalı sistemler için tanımlanmıştır.
Buna göre entropi sadece bulunan hallere bağlı olduğundan hal fonksiyonu
olarak tanımlanmıştır. Entropinin hesabı için;
1-Başlangıç bitiş halleri için olan 1 ve 2 hali tanımlanmalı
2-Bunun için tersinir bir yol belirlenmelidir.
3- ΔS=
ter/T
formülü kullanılarak ΔS hesaplanmalıdır.
37
Bu ister tersinir ister tersinmez olsun takip edilmesi gereken yoldur.
Chakrabarty (2001)’ye göre gazların kinetik teorisine göre yüksek ısı,
taneciklerin çok daha fazla gelişi güzel hareket yapmasına sebep olmaktadır. Buna göre,
yüksek entropiye sahip bir sistem daha fazla ısıya sahiptir. Entropi artan bu ısı miktar
mıdır acaba? Eğer böyleyse ısı miktarı yola bağlı olup hal fonksiyonu değildir.
Dolayısıyla entropide sonsuz küçük bir değişim teoride tam diferansiyel almayacaktır.
Ancak yine ona göre entropinin in bir hal fonksiyonu olarak tanımlanması çok büyük
kolaylık sağlamaktadır.
Glasstone ve Lewis(1978)‘in dediğine göre sistemin gerçek entropisi kolaylıkla
tanımlanamaz bunun yerine entropideki artışın tanımlanması çok daha pratiktir.
Dolayısıyla entropideki
ΔS artışın tanımlanması çok daha pratiktir. Dolayısıyla
entropideki ΔS artışı tersinir bir prosesteki dq
ter/T
eşittir. Δ q ter değeri tam bir
diferansiyel olmamasına rağmen bunun tersinir ve izotermal bir değişiminin net bir
değer olduğundan yukarıda tanımlanan ΔS’inde tam diferansiyel olduğu söylenebilir.
Buna göre sistemin entropisi olan S değeri sadece hal ve durumuna bağlıdır ve aradaki
yola bağlı değildir. Dolayısıyla ΔS değeri (S2-S1) sadece başlangıç ve bitiş hallerine
bağlı olup aradaki yolun tersinir veya tersinir olmasına bağlanamaz. Ancak
ΔS
değerinin gerçek değerini bulmak için ısının tersinir bir biçimde soğrulması gerekir. dq
ter
eğer ısı tersinmez olarak soğrulduysa belirsiz bir değer olup entropi hesabında
kullanılmaz.
Barrow(1979), Carnot çevrimine dayanarak entropi direk olarak bir hal
fonksiyonu olarak kabul etmiş ve aynı şekilde entropinin sistemin başlangıç ve bitiş
hallerine bağlı olduğundan oraya nasıl geldiğinin önemli olmadığını vurgulamıştır. Yani
direkt olarak entropinin hal fonksiyonu olduğunu kabule etmiştir. Ancak burada da
Clausius eşitliğine bir açıklama getirmemektedir.
Voltehc vd. (1977) entropinin hal fonksiyonu olmasını her dq
ter/T’
nin bir hal
fonksiyonu olması gerektiğini söylemiştir. Entropinin kendiliğinden olan olayların
önemli bir fonksiyon olduğunu belirlemiştir. Entropinin
herkes gibi Carnot çevrimine dayandırmış ve
söylemiş.
dq
ter/T’
hal fonksiyonu olduğunu
nin tam diferansiyel olduğunu
38
Bery vd.(1986) entropinin S=KB ln Ώ (E,V,N) şeklinde kuantum kimyasal
tanımını yapmıştır. Ancak entropinin sadece makroskopik değerlere bağımlı tanımı da
kolaylıkla yapılabilir.
Termodinamiğinin II. Kanunu yazılı olarak 3 şekilde ifade edilebilir.
Birincisi, Clausius ifadesi: Buna göre, sıcak bir ısı deposundan soğuk bir ısı
deposuna ısı aktarmak dışında herhangi bir etki yapmadan çalışan çevrimsel bir makine
yapılamaz.
İkincisi, Kelvin tanımı: Buna göre, çevresinde sıcak ısı deposundan ısı alıp
tamamını işe döndürecek bir makine yapmak mümkün değildir.
Üçüncüsü ise Caratheodory: Buna göre her denge halindeki bir halin çevresinde
herhangi bir adyabatik bir yol ile 1. Halden başlamak suretiyle erişilmeyecek haller
vardır. Görüldüğü gibi I.Kanundan aksine burada erişilmesi imkansız haller vardır.
Buna göre iki tane tersinir adyabat veya izotermin kesişmesi mümkün değildir .
Arada hiçbir adyabatik tersinir bir yol yoksa bu durumda sistemin entropisi
sadece ΔS=S1-S2′
yazılır. ΔS değeri S1-S2+S2′ olup S1-S=0’dır. Dolayısıyla
S2-S2′=q2′/T>0 dolayısıyla ΔS>0 olup 2 ile 1 arasındaki her türlü tersinmez prosesler
için geçerlidir. Dolayısıyla dS ≥ dq/T olup entropinin hal fonksiyonu olmasına tamamen
ters bir durum arz etmektedir. Kısaca, Clausius eşitsizliği entropinin hal fonksiyonu
olma şartına ters düşmektedir.
Adamsan (1979) burada sadece izotermal bir çevrim ile ısıyı işe çevirmek
mümkün olmadığı ve kapalı sistemlerde entropinin kendiliğinden olan prosesler de
artacağını ve qter/T’nin de hal fonksiyonu olduğunu söylemektedir. Kısaca, entropi
kapalı sistemler için söz konusu olan bir kavramdır.
Burada en net açıklamayı Glasstone (1975) getirmiştir. Glasstone‘e göre
dS=dq/T olup dq’nun tersinir ve izotermal bir proses tam diferansiyel olmamasına
rağmen dS′ değerinin tam diferansiyel olduğunu göstermiştir.1 ve 2 halleri arasında
integral alındığında ΔS= S2-S1. Buna göre S1 başlangıç hali, S2 de son halindeki entropi
olup yukarıdaki açıklamaya göre sadece bu hallere bağlı olup aradaki yola bağlı
değildir. Bu yolun tersinir olup olmadığına bağlı olmaksızın S2-S1 değeri aynıdır. Ancak
ΔS değeri yukarıdaki denklemde bulunması durumunda da değerinin de sabit T’de
39
tersinir bir değişim olması gerekir. Eğer değişim tersinmez ise soğrulan ısı belirsiz olup
entropi artışını belirlemede kullanılamaz. Adyabatik bir proseste sistemi herhangi bir ısı
girmediğinden dq=0 olup entropide bir değişim söz konusu değildir bu yüzden bu tip
değişimlere izentropik(sabit entropi) değişim denir.
Castellan (1983) entropiyi II. Kanuna göre tanımlamış. Entropinin Carnot
çevrimindeki değerin sıfır olmasından dolaylıda buna hal fonksiyonu olduğunu
belirtmiş. Ancak Clausius eşitsizliği ile gösterilen tersinir ve tersinmez haldeki entropi
değişiminin farklı olması olayına farklı bir açıklama getirmemiştir.
Kriev (1978) II. Kanunun önemini açıkladığı 7. Bölümümde doğal olayları 3’e
ayırmıştır.
1. Sisteme meydana gelen değişime direk olarak orantılı olan bir işin yapılması
gerektiği olaylar
2. Sisteme bir işin yapılmasını gerektirmeyen ve dış kuvvetlere karşıda herhangi
bir iş elde edilmeyen olaylar
3. Kendiliğinden gelişen olaylardaki sistem üzerine herhangi bir iş yapılmasını
gerektirmeyen meydana gelen değişim ile orantılı olan bir işin elde edildiği olaylardır.
1. tip olaylara bir cismi yükseğe kaldırmak veya suyun bir elektrik akımı etkisi ile
bulunması örnek verilebilir.
2. tip olaylara ise bir topun tamamen yatay bir düzlemde hareket etmesi veya
sürtünmesiz bir sarkacın titreşimleri örnektir.
3. tip olaylara ise genel olaylar olup ağırlığın aşağı düşmesi, kuvvetli bir asitin kuvvetli
baz tarafından nötralize edilmesi yakıtın yanması, maddelerin camsı halden kristal hale
geçmesi örnek verilebilir. Bu gruptaki olayların hepsi pozitif olaylar olarak bilinir.1.
gruptaki olaylar ise negatiftir.
Buna göre I. Kanun sistemin oluşumu karakteri hakkındaki herhangi bir şey
söylemezken II. Kanun verilen P, T ve konsantrasyonda olayın kendiliğinden oluşup
oluşmayacağı hakkında bilgi verir.
Buna göre enerji bir şiddet faktörü ile kapasite faktörünün bir çarpımıdır. Şiddet
faktörü madde miktarından bağımsız olup kapasite faktörü madde miktarı ile değişir.
40
Bir olayın olabilirliği şiddet faktörü ile arasındaki ilişkiye bağlıdır. Örneğin, biri
sıcak , biri soğuk iki cisim birbiri ile temasa getirilirse sıcak cismin sıcaklığı azalırken
soğuk cismin sıcaklığı artar. Bu olay denge haline kadar devam eder. Bu tip denge
olaylara çok fazla örnek mevcuttur. Dolayısıyla kendiliğinden oluşan bu olayların
yönünü ve sınırlarını belirleyen bir kriter alınmalıdır. Buna göre; farklı kısımlarında
meydana gelen olayları belirleyen faktör sistemi denge durumuna götürecek yönde
hareket etmelidir.
Bu olay sadece ve sadece homojen sistemlere uygulanabilir. Buna göre
Termodinamik II. Kanunu verilen şartlar altında her termodinamik sistem için bunun
yönünü olabilirliğini, sınırı tanımlayan genel bir kıstas olduğunu söyler.
Örneğin izole sistemlerde bu parametreye entropi denir. Diğer şartlar için daha
farklı termodinamik parametrelerin kullanılması daha uygundur.
II. Kanuna göre izole sistemler sistemin entropisinin artması ve maksimum
değere ulaşması durumunda kendiliğinden cereyan eder.
Ayrıca entropinin istatistik termodinamik yanı da vardır. Buna göre izole bir
sistemde ısı, sıcak cisimden soğuk bir cisme akarken sistemin entropisi artar dolayısıyla
tersinmez sistemlerde mutlaka bir entropi artışı söz konusudur. Buna göre ∫dq/ T< 0
olmalıdır. Entropi hal fonksiyonu olduğuna göre prosesin gittiği yoldan bağımsız olup
özellikle sistemin tersinirliği üzerinde hiçbir etkisi yoktur. Eğer sistem orijinal haline
dönerse bu çevriminin şartıdır. Entropide daima ilk değerini alır. Dolayısıyla entropi
değişimi sıfırdır. Ancak prosesin ısısı yola bağlı olduğundan yukarıdaki eşitsizlik denge
durumuna uygulanmaz .İstatistiktik termodinamiğe göre entropi taneciklerin farklı
hareket türleri ile ilgili termodinamiğin toplamıdır. Tüm bu yukarıdakilerin anlatımına
göre dS ≥ dq/T buna göre izole bir sistemde ( sadece adyabatik olayların cereyan
edebildiği) sistemin entropisi ancak tersinir bir proses meydana gelebiliyorsa sabit olup
tersinmez bir sistemde mutlaka artar .Başka bir deyişle izole bir sistemde kendiliğinden
meydana gelen her olay sonunda entropi artar.
Mortimer (1993)’’e göre tersinir bir sistemde entropi başlangıç ve bitiş hallerine
bağlı olduğunda gidilen yola bağımlı değildir dolayısı ile hal fonksiyonudur. Tersinmez
durumda ise sistem bir seri denge halinde geçerek son hale gelir. Başlangıç ve bitiş
halleri denge değildir. Dolayısı ile bu durumda entropi bir hal fonksiyonunu olmaz.
41
Bir proses alırsak ve bu durumda 2. Noktasındaki sıcaklık 1 noktasındakinden
daha yüksek olursa q döngü=q2<0 olur. Wçevre=- W döngü= -ΔUdöngü+ q2< 0
Bu durumda alınan tüm ısı tamamen çevreye aktarılmış olur ki bu durumun
termodinamiğin II. Kanunu ihlal etmez dolayısıyla tersinmez bir adyabatik değişim
daima tersinir bir sistemdeki
tersinir=∫c
daha yüksek sıcaklıklarda sonlanır. Dolayısıyla
ΔS
dqtersinir/T=0 (tersinir adyabatik proses )
ΔS tersinmez> 0 olmaktadır. ( tersinmez adyabatik proses )
ΔS ≥ 0 ( genel adyabatik proses)
Alberty (1983)Carnot çevrimine göre q1 / T 1+q2 / T2 =0Buna göre q / T bir hal
fonksiyonudur. Bu tersinmez sistemlerde 2 durum söz konusudur. Bunlardan bir
tanesinde tersinir adyabatik proses sonucunda entropi artmakta diğerinde ise
azalmaktadır. Düz çizgiler tersinir prosesleri göstermek kaydıyla her 2 diyagram içinde
W2+ W23 + W31 + q23 =0
Eğer q23 pozitif ise buna göre sistem ısı soğurmuş demektir ki bu 2. Kanunun
ihlalidir.2-a daki proses mümkün değilmiş.
Eğer q23 negatif ise sistem çevrimi prosesi sonunda dışarı ısı verir ki, buda iş
elde etmek için kullanılabilir. Buna göre ΔS sistem + ΔS ortam ≥0 durumuna göre ΔS
ortam=
-q sistem / T
ΔS sistem ≥ q sistem / T ‘dir.
buna göre izole bir sistemde tersinmez veya kendiliğinden olan prosesin entropileri
maksimuma çıkar. Şu ana kadar söylenen her şey izole adyabatik sistemler için
geçerlidir.
5.SONUÇ VE ÖNERİLER
Termodinamiğin II. ve III. Kanunlarına göre entropi sistemdeki düzensizliğin bir
ölçüsü olarak farz edilip olayların kendiliğinden olması(tersinmez olması) temel
42
parametredir. Buna göre entropi kendiliğinden olan olaylarda pozitif olmalıdır. Ayrıca
entropi termodinamiğin III. Kanuna göre olasılığın bir fonksiyonudur.
Ancak bunların tersini gösteren birçok örnek vardır. Bunun için aşağıdaki
sistemlere bakalım:
Şekil 5.1 Entropinin negatif çıkması durumunda bile olayın kendiliğinden olması
Buradan da görüldüğü gibi kendiliğinden cereyan eden bu üç prosesin olasılık
açısından entropik değişimleri sıfırdan küçük, sıfır ve sıfırdan büyük çıkmaktadır.
.
Dolayısıyla entropiyi olasılık değişimi olarak almak doğru değildir. Yukardaki şekiller
ilk başlangıç anına göre verilmiştir Tabi bir süre sonra gaz tüm hacimi doldurur.
Entropiye düzensizlik ve olasılık olaylarına bağlayıp onu da kendiliğinden olan
olaylarda entropi artış ile ilişkilendiren teoriler karşı çıkan birçok örnek mevcuttur
(Şekil 5.2 ).
Ayrıca
fizikokimyada
kendiliğinden
olan
tersinmez
olaylara
karışma
kendiliğinden olmayan tersinir olaylara da ayrışma örnek verilir ama aşağıdaki örnekler
bunu yalanlamaktadır ( Şekil 5.2 ).
43
Şekil 5.2 Ayrışmanın kendiliğinden olması
Burada da görüldüğü üzere ayrılma prosesi de kendiliğinden gerçekleşmedir.
Yukardaki şekiller ilk başlangıç anına göre verilmiştir Tabi bir süre sonra gaz tüm
hacimi doldurur.
Bunun yanı sıra entropi sadece kapalı ve izole sistemlerde artarken bu tüm
proseslere mal edilmekte ve sadece sistemin entropisi alınarak toplam entropi kaale
alınmamaktadır .
Bunun yanı sıra entropinin hal fonksiyonu olması durumunda hem entropinin
korunumsuzluğu hem de Clausius kanunu ile ters düşmektedir. Tersinmez bir durum
için olan entropi hesabı bile tersinir bir yol üzerinden yürütülmektedir. Buna göre
entropi düzensizlik değil mikro hallerin ve enerjinin dağılımı ile ilgilidir.
Bu kavram son derece karmaşık ve içinden çıkılmaz bir hal alabilir. Bir kere
hangi değişimin entropisi hal değişim fonksiyonudur? Sisteminki mi ( ki açıkça değil)
ortamınki mi evreninki mi? Entropi nasıl olurda hem hal fonksiyonu olur hem de
korunmayarak sürekli artar? Ayrıca entropinin ortamın düzensizliğine eşit olduğu savı
44
da doğru olmayıp ancak istatistiksel olarak mikro hallerin veya enerjinin bir dağılımı
olduğu şeklinde bir açıklama getirilebilir. Bu kavramın makro sistemler için kullanımı
son derece büyük sorun meydana getirmektedir.
Buna göre entropi yerine serbest enerji (G) değişiminin kullanılması tüm bu
karışıklığı giderebilir. Tersinmez olaylarda (kendiliğinden olan olaylarda) serbest enerji
değişimi negatif olmalıdır.
45
KAYNAKLAR
Adamson, A.W, (1979)A Text of Phy.Chem, Universty of Southern
California,S. 172- 177
Albert, R.A. and Silbey, J.(1992) Phy. Chem., First Ed.,
Atkins, P. W(1998) Physical Chemistıy, 6th ed.; Oxford University Press, Oxford ,
Melbourn, Tokyo,
Barrow,G:M., Physical Chemistry,4th ed., McGraw-Hill, London
Berry, R.S., Rice, S.A., Ross, J., 1986, Phy.Chem.,
Castellan, G.W., 1983, Phy. Chem., Third Edi., Universty of Maryland
Chakrabarty, DK.,2001, An Intoduction To, Physical Chemistry ,McGraw Hill
Glasstone, S., Lewis, D., 1978, Element of Physical Chemistry, Second Edn. McGraw
Hill
Glasstone.S, 1975, The Elements Of Physical Chemistry, McGraw Hill
Gordon M. Barrow, Physical Chemistry , 4th ed. McGraw Hill ,1978
Kriev, V., 1978, Physical Chem. , Chapter7,
Lechner, J. H. 1999. Visualizing Entropy, Journal of Chemical Education, 76 (10),
1382-1385
Levine, I, N, 1988, Physical Chemistry, Third Edition, McGraw- Hill, Book Co.
Singapore.
Maes, C. and Redig, F., 2000, Positivity of Entropy Production, Journal of Statistical
46
Physics, 101(1-2), 3-15.
Selepe, C. and Bradley, J. 1997).Student-Teacher’s Conceptual Difficulties in Chemical
Thermodynamics. In M. Sanders, (Ed), SAARMSE Fifth Annual Meeting (pp. 316321). Universty of the Witwatersand, Johannesburg, South Afrika, 1997.
Sözbilir, M., 2001, A Study of Undergraduates’ Understandings of Key Chemical Ideas
in Thermodynamics (D. Phil, thesis), Department of Educational Studies, University of
York, UK.
Thomas P. L. and Schwenz, R.' W. 1998, “College physical chemistry students’
conceptions of equilibrium and fundamental thermodynamics,” J. Res. Sci. Teach. 35,
1151 -1160.
Vojtech, F., Hameka, H.F., Blukis, U., 1997,Phys. Chem
Walter J. 1972, Moore Physical Chemistry, Universty of Sydney,