2- ARTAN ve AZALAN FONK..qxp

Artan ve Azalan Fonksiyonlar
ii)
y
y
2. ARTAN VE AZALAN FONKSÝYONLAR
Teorem :
f(x1)
f : (a, b) → R,
y = f(x) fonksiyonu ∀x ∈ (a, b) için sürekli
ve türevlenebilen bir fonksiyon olsun.
f(x2)
a x1
x
x2 b
a
b
x
x deðerleri (a, b) aralýðýnda x 1 den x 2 ye
artan deðerler alýrken fonksiyonun alacaðý
deðerler azalandýr.
x1 < x2
⇒ Δx = x 2 − x 1 > 0
ý
1) ∀x ∈ (a, b) için f (x) > 0 ⇔
f(x) fonksiyonu bu aralýkta artandýr.
ý
2) ∀x ∈ (a, b) için f (x) < 0 ⇔
f(x) fonksiyonu bu aralýkta azalandýr.
f(x 1 ) > f(x 2 )
ý
3) ∀x ∈ (a, b) için f (x) = 0 ⇔
f(x) fonksiyonu bu aralýkta sabit bir
fonksiyondur.
Buradan
Buradan
Ýspat :
⇒ Δy = f(x 2 ) − f(x 1 ) < 0
Δy f(x 2 ) − f(x1)
=
<0
Δx
x 2 − x1
lim
Δx → 0
Δy
= f ý (x) < 0
Δx
yazýlabilir.
ý
O halde ∀x ∈ (a, b) için f (x) < 0 olur.
i)
y
y
Baþka bir deyiþle f(x) fonksiyonu (a, b)
aralýðýnda azalan bir fonksiyon olup aralýðýn her noktasýndan fonksiyona çizilen
teðetlerin ox ekseni ile yaptýðý açýlar geniþ
açýlardýr. Geniþ açýlarýn tanjantlarý negatif
olduðundan f(x) in (a, b) aralýðýnýn her noktasýndaki türevi de negatiftir.
f(x2)
f(x1)
α
a x1
x2 b
α
x
a
b
x
ý
m = tanα = f (x) < 0 dýr.
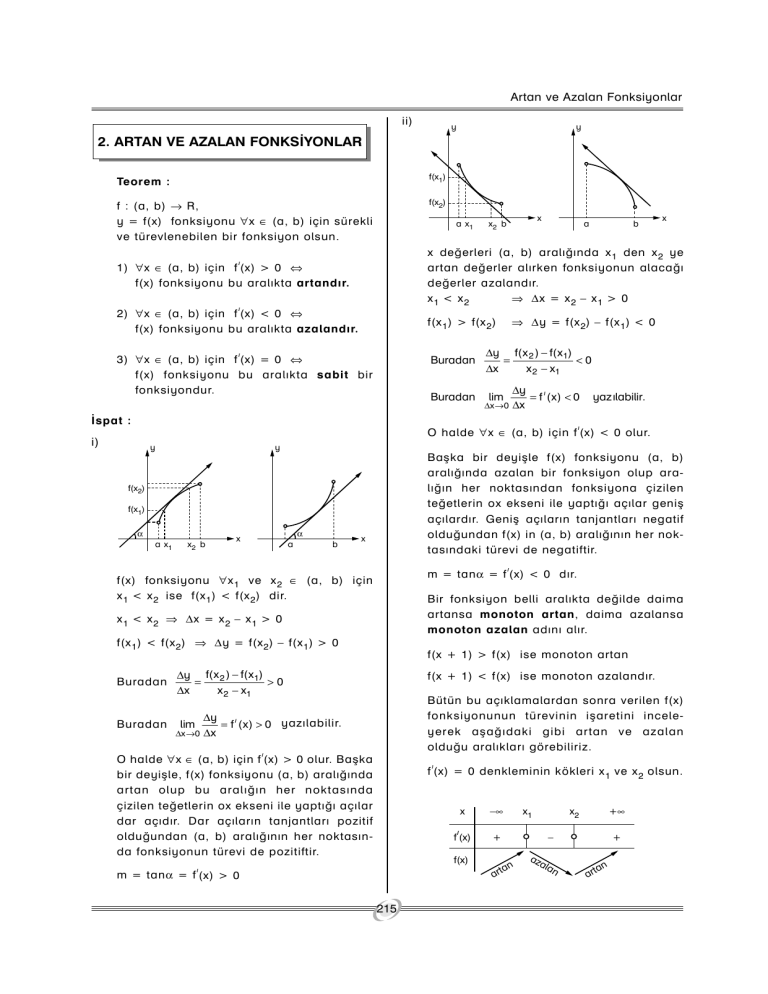
f(x) fonksiyonu ∀x 1 ve x 2 ∈ (a, b) için
x 1 < x 2 ise f(x 1 ) < f(x 2 ) dir.
Bir fonksiyon belli aralýkta deðilde daima
artansa monoton artan, daima azalansa
monoton azalan adýný alýr.
x 1 < x 2 ⇒ Δx = x 2 − x 1 > 0
f(x 1 ) < f(x 2 ) ⇒ Δy = f(x 2 ) − f(x 1 ) > 0
Buradan
f(x + 1) > f(x) ise monoton artan
Δy f(x 2 ) − f(x1)
=
>0
Δx
x 2 − x1
f(x + 1) < f(x) ise monoton azalandýr.
Bütün bu açýklamalardan sonra verilen f(x)
fonksiyonunun türevinin iþaretini inceleyerek aþaðýdaki gibi artan ve azalan
olduðu aralýklarý görebiliriz.
Δy
Buradan lim
= f ý (x) > 0 yazýlabilir.
Δx →0 Δx
ý
O halde ∀x ∈ (a, b) için f (x) > 0 olur. Baþka
bir deyiþle, f(x) fonksiyonu (a, b) aralýðýnda
artan olup bu aralýðýn her noktasýnda
çizilen teðetlerin ox ekseni ile yaptýðý açýlar
dar açýdýr. Dar açýlarýn tanjantlarý pozitif
olduðundan (a, b) aralýðýnýn her noktasýnda fonksiyonun türevi de pozitiftir.
ý
f (x) = 0 denkleminin kökleri x 1 ve x 2 olsun.
x
−∞
f (x)
+
ý
f(x)
ý
m = tanα = f (x) > 0
215
x1
x2
+∞
+
−
n
a
art
az
ala
n
an
art
Artan ve Azalan Fonksiyonlar
Örnek 1
Örnek 3
f(x) R → R, f(x) = x 2 − 4x + 2
fonksiyonunun artan ve azalan olduðu
aralýklarý bulunuz.
f(x) R → R,
türevinin
Çözüm
iþaretini
ý
f (x) in iþareti daima negatif olmalýdýr.
Bunun için,
ý
f (x) = 2x − 4 ⇒ 2x − 4 = 0
x = 2
x
ý
f (x)
f(x)
ý
2
−∞
f (x) = −x 2 + 2mx − 4 = 0 denkleminde
a < 0 ve Δ < 0 olmalýdýr. Buna göre;
+∞
Δ = b 2 − 4ac = (2m) 2 − 4.(−1).(−4) < 0
+
−
az
f(2)
ala
n
1 3
x + mx 2 − 4x + 1
3
fonksiyonunun daima azalan olmasý için
m ne olmalýdýr?
Çözüm
f(x) fonksiyonunun
inceleyelim.
f(x) = −
= 4m 2 − 16 < 0 ⇒ m 2 < 4
|m| < 2
−2 < m < 2 bulunur.
n
rta
a
O halde fonksiyon (−∞, 2) aralýðýnda
ý
f (x) < 0 olduðundan fonksiyon azalan,
ý
(2, +∞) aralýðýnda f (x) > 0 olduðundan
fonksiyon artandýr.
Örnek 4
f(x) R → R, f(x) = x 3 + 6x − 2
fonksiyonunun artan ve azalan olduðu
aralýklarý bulunuz.
Örnek 2
f(x) = x 3 − 6x 2 − 36x + 5
fonksiyonunun artan ve azalan olduðu
aralýklarý bulunuz.
Çözüm
f(x) fonksiyonunun
inceleyelim.
Çözüm
türevinin
iþaretini
ý
f(x) fonksiyonunun
inceleyelim.
türevinin
ý
f (x) = 3x 2 − 12x − 36 ⇒
f (x) = 3x 2 + 6 ⇒ 3x 2 + 6 = 0
iþaretini
denkleminin reel kökleri yoktur. Dolaysýyla
a > 0 olduðundan türevi daima pozitif olacaktýr. O halde fonksiyon daima artandýr.
Buna monoton artan da denir.
3x 2 − 12x − 36 = 0
3(x2 − 4x − 12) = 0
3(x + 2)(x − 6) = 0
O halde fonksiyonun artan olduðu aralýk
tüm reel sayýlardýr.
Buradan x = −2 ve x = 6 bulunur.
x
−∞
f (x)
+
ý
6
−2
+∞
f(x)
ar
tan
az
ala
n
Örnek 5
+
−
f : R −{−1} → R, f(x) =
tan
ar
ax + 2
x +1
fonksiyonu x = − 1 noktasýnýn dýþýnda her
yerde artan olabilmesi için a ne olmalýdýr?
Tabloda görüldüðü gibi,
~ (−∞, −2) ∪ (6, +∞) aralýðýnda
ý
f (x) > 0 olduðundan fonksiyon artan
Çözüm
f fonksiyonu x = −1 in dýþýnda daima artan
ise,
~ (−2, 6) aralýðýnda
ý
f (x) < 0 olduðundan fonksiyon azalandýr.
ý
x ∈ R −{−1} için f (x) > 0 olmalýdýr.
216
Artan ve Azalan Fonksiyonlar
Çözüm
Buna göre,
f ý (x) =
=
a.(x + 1) − 1 . (ax + 2)
2
(x + 1)
a−2
=
ax + a − ax − 2
(x + 1)
Soruda türevin grafiði verildiðine göre bu
grafikten türevin iþaretini bir tablo ile
gösterebiliriz.
2
> 0 ⇒ a − 2 > 0 buradan
(x + 1)2
a>2
bulunur.
ý
f(x)
ala
an
n
art
1
, f 2 (x), f (x 2 ), (fof)(x)
f(x)
−f(x),
iþaretini
fonksiyonlarýnýnda artan veya azalan
olup olmadýklarýný gösteriniz.
Çözüm
f(x) fonksiyonu (0, +∞) aralýðýnda artan ise
ý
ayný aralýkta f (x) > 0 dýr. Buna göre,
+∞
a)
+
−
az
az
f(x) fonksiyonu (0, +∞) aralýðýnda artan ve
∀x ∈ (0, +∞) için f(x) > 0 ise
2
e x − 6x + 4 ≠ 0 ⇒ 2x − 6 = 0
x = 3 tür.
f (x)
+
−
Örnek 8
ý
2
f (x) = (2x − 6) . e x − 6x + 4 = 0
3
+∞
Bu tabloya göre,
f(x) fonksiyonu, (−∞, −3) ve (1, +∞) aralýklarýnda artan (−3, 1) aralýðýnda ise azalandýr.
Çözüm
−∞
+
an
2
f : R → R, f(x) = e x − 6x + 4
fonksiyonunun artan ve azalan olduðu
aralýklarý bulunuz.
x
f (x)
1
−3
art
Örnek 6
türevinin
−∞
ý
Uyarý :
Bu þekildeki kesirli fonksiyonlara R de
artandýr veya azalandýr denilmez. Çünkü
fonksiyonu tanýmsýz yapan sayýlar vardýr.
f(x) fonksiyonunun
inceleyelim.
x
ala
ý
an
n
art
ý
(−f(x) ) = −f (x) < 0 olduðundan −f(x) fonksiyonu ayný aralýkta azalandýr.
ý
b)
O halde (−∞, 3) aralýðýnda fonksiyon azalan, (3, +∞) aralýðýnda fonksiyon artandýr.
⎛ 1 ⎞
− f ý (x)
< 0 olduðundan ayný aralýkta
⎜
⎟ =
f(x)2
⎝ f(x) ⎠
1
fonksiyonu azalandýr.
f(x)
Örnek 7
y
c)
ý
f (x)
ý
( f(x) 2 ) = 2 f(x) . f ý (x) > 0
N
N
olduðundan ayný
+
+
aralýkta f (x) 2 fonksiyonu artandýr.
−3
1
d)
x
ý
f ý (x 2 ) . 2x > 0
N
( f(x 2 ) =
olduðundan ayný
+
+
aralýkta f (x 2 ) fonksiyonu artandýr.
f(x) fonksiyonunun türevinin grafiði yukarýda verilmiþtir.
e)
ý
[(fof)(x)] =
ý
f ý (f(x)) . fN
(x) > 0
+
olduðundan
+
ayný aralýkta (f of)(x) fonksiyonu da artandýr.
Buna göre, f(x) in artan ve azalan olduðu
aralýklarý bulunuz.
217
Artan ve Azalan Fonksiyonlar
Örnek 9
y
x = 2t 3 + t
mutlak mak.
y = t 2 − 2t
4
5
þeklinde tanýmlanan parametrik fonksiyonunun R’de artan veya azalan olduðu
aralýklarý bulunuz.
3
p
a
dy yý (t)
2t − 2
f ý (x) =
=
=
dx x ý (t) 6t 2 + 1
olduðundan f (x) > 0 ⇔ 2t − 2 > 0
(Paydanýn daima pozitif olduðunu görünüz.)
l m
2
n t
3
u
4
b
x
Yerel minimum deðerlerinin en küçüðüne
mutlak minimum veya fonksiyonun en
küçük deðeri denir.
x = 2t 3 + t = 2.1 3 + 1 = 3 den büyük
deðerler alacaðýndan, fonksiyonun artan
olduðu aralýk (3, +∞) aralýðýdýr
.
EKSTREMUM NOKTALAR ÝLE TÜREVÝN
ÝLÝÞKÝSÝ
Benzer þekilde
ý
f (x) < 0 ⇔ 2t − 2 < 0 ⇒ t < 1 dir.
⇒
k
Yerel maksimum deðerlerinin en büyüðüne
mutlak maksimum veya fonksiyonun en
büyük deðeri denir.
x ve y, t deðiþkenine baðlý olduðundan t’ye
1’den büyük deðerler verildikçe x’de
x = 2t 3 + t
q
−2
mutlak min.
Bir fonksiyonun birden fazla yerel (baðýl)
maksimum ve minimum deðerleri olabilir.
ý
2t − 2 > 0 ⇒ t > 1 dir.
~
yerel min.
2
Çözüm
~
yerel mak.
t = 1 için x = 3
Teorem (Fermat Teoremi) :
t’ye 1’den küçük deðerler verildikçe x’de
3’den küçük deðerler alacaðýndan, f(x) in
azalan olduðu aralýk (−∞, 3) aralýðýdýr.
f : [a, b] → R fonksiyonu sürekli ve (a, b)
aralýðýnda türevli olsun. f(x) in x o ∈ (a, b)
noktasýnda yerel ekstremumu varsa
ý
f (x o ) = 0 dýr.
YEREL MAKSÝMUM VE MÝNÝMUM
NOKTALAR
Bu teoremin karþýtý her zaman doðru
ý
olmayabilir.
Yani, f (x o ) = 0 olduðu halde
ý
(x o , f (x o ) ) noktasýnda yerel ekstremumu
olmayabilir.
(YEREL EKSTREMUM NOKTALAR)
f : A → R, y = f(x) fonksiyonunda a ∈ A ve
ε yeterince küçük pozitif bir reel sayý olmak
üzere a noktasýný içine alan (a − ε, a + ε )
aralýðýndaki her x sayýsý için;
~
f(x) ≤ f(a) ise (a, f(a)) noktasýna fonksiyonun yerel (baðýl) maksimum noktasý,
f(a) deðerine de fonksiyonun yerel maksimum deðeri denir.
~
Eðer f(x) ≥ f(a) ise (a, f(a)) noktasýna
fonksiyonun yerel (baðýl) minimum noktasý, f(a) deðerine de fonksiyonun yerel
minimum deðeri denir.
Örnek 1
y
y = x3
x
f : R → R, f(x) = x 3
ý
fonksiyonu f (0) = 0 olduðu halde (0, 0)
noktasý fonksiyonun yerel ekstremum noktasý deðildir.
218
Artan ve Azalan Fonksiyonlar
Uyarý :
Bir f(x) fonksiyonunun x 1 apsisli noktada
yerel ektremumu (maksimum veya minimumu) olduðu halde fonksiyonun bu noktada
türevi olmayabilir.
y
x
c
−∞
fý (x)
f(x)
−
+
c
+
−
az
f(c)
ala
+
x
+∞
n
tan
ar
−
+ −
Örnek 2
(c, f(c) ) minimum noktadýr.
f : R → R, f(x) = |x − 2| + 1
fonksiyonunun yerel ekstremum noktasýný bulunuz.
NOT :
Türevlenebilen bir fonksiyonun birinci türevinin kökleri yerel maksimum veya yerel
minimum noktalarýnýn apsisleridir. Bu noktalar esas fonksiyonda yerine yazýlarak
ordinatlarý da bulunabilir.
Çözüm
y
f(x) in grafiðinde de
görüldüðü gibi fonksiyonun A(2, 1) noktasýnda bir yerel minimum deðeri olduðu halde, x = 2
noktasýnda türevi;
3
2
1
A
x
2
1
ý
ý
x
ý
f (x)
x ≥ 2 ise f(x) = x − 1 , f (x) = 1 ⇒ f (2 + ) = 1
ý
ý
x < 2 ise f(x) = −x + 3 , f (x) = −1 ⇒ f (2−) = −1
ý
ý
f (2 + ) ≠ f (2 − ) olup bu noktada türevi yoktur.
1)
f(x)
BÝRÝNCÝ TÜREVDEN YARARLANILARAK
EKSTREMUM NOKTALARININ ÝNCELENMESÝ
f : (a, b) → R’ye tanýmlý ve türevlenebilen
bir fonksiyon verilmiþ olsun.
i)
x
c
−∞
fý (x)
+ −
+
f(x)
−
+
c
+
−
x
tan
ar
x1
+
x2
+∞
+
−
f(x1)
f(x2)
max.
min.
~
(x 1 , f(x 1 ) ) noktasý yerel maksimum noktasýdýr.
~
(x 2 , f(x 2 ) ) noktasý yerel minimum noktasýdýr.
+∞
Örnek 3
−
f : R → R, f(x) = x 3 − 3x 2 + 6
fonksiyonunun yerel ekstremum noktalarýný bulunuz.
f(c) az
a
lan
Çözüm
f(x) in türevinin iþaretini inceleyelim.
(c, f(c) ) maksimum noktadýr.
ý
ii)
−∞
Uyarý :
Türevlenebilen bir fonksiyonun yerel
ekstremum noktasýnýn olabilmesi için
türevinin bu noktada iþaret deðiþtirmesi
gerekir.
f(x) fonksiyonu bir x = c noktasýnýn solunda artan saðýnda azalan ise x = c, f(x) in
bir maksimum noktasýdýr.
y
max.
min.
f (x) = 3x 2 − 6x ⇒ 3x 2 − 6x = 0
3x(x − 2) = 0
Buradan x 1 = 0 ve x 2 = 2
f(x) fonksiyonu bir x = c noktasýnýn solunda azalan saðýnda artan ise x = c, f(x) in
bir minimum noktasýdýr.
219
Artan ve Azalan Fonksiyonlar
x
−∞
f′(x)
0
2
+
f(x)
+
−
6
~
+∞
2
(−2, 0) aralýðýnda f(x) azalan (0, +∞)
aralýðýnda f(x) artan olduðundan x = 0
apsisli nokta f(x) in yerel minimum noktasýdýr.
Örnek 6
f(0) = 6, (0, 6) noktasý maksimum nokta
f(2) = 2, (2, 2) noktasý minimum noktadýr.
f(x) = x 3 − mx 2 + nx + 5 fonksiyonunun
x = 1 apsisli noktadaki yerel ekstremum
deðeri 7 olduðuna göre m + n nin deðeri
kaçtýr?
Örnek 4
f(x) = x 2 − (m − 1)x + m + 2
3
fonksiyonun x =
de bir maksimumu
2
olduðuna göre m’nin deðeri kaçtýr?
Çözüm
f(x) in x = 1 de bir yerel ekstremumu
ý
olduðuna göre f (1) = 0 dýr. Buna göre;
Çözüm
f(x) in x =
3
de bir yerel maksimumu varsa,
2
ý
ý
f (x) = 3x2 − 2mx + n ⇒ f (1) = 3 − 2m + n = 0
−2m + n = −3
ayrýca x = 1 de f(1) = 7 olduðundan
⎛3⎞
fý ⎜ ⎟ = 0 olmalýdýr.
⎝2⎠
f(1) = 1 − m + n + 5 = 7
−m + n = 1 dir.
ý
f (x) = 2x − (m − 1)
Bu denklemleri ortak çözdüðümüzde,
3
⎛3⎞
f ý ⎜ ⎟ = 2 . − m + 1 = 0 ⇒ m = 4 bulunur.
2
⎝2⎠
m=4
2m − n = 3 ⎫⎪
⎬⇒ n = 5
−m + n = 1 ⎪⎭
ise m + n = 9 bulunur.
Örnek 5
f : R → R, f(x) =
Örnek 7
3 4
x + 8x 3 + 12x 2 + 5
2
f : R → R, f(x) = x 3 − ax 2 + (b − 1)x + 5
fonksiyonunun x = −2 ve x = 1 de yerel
ekstremumlarý olduðuna göre a ve b kaç
olmalýdýr?
fonksiyonunun yerel ekstremum noktalarýný bulunuz.
Çözüm
ý
f (x) =
ý
f (x) =
Çözüm
3
.4x 3 + 24x 2 + 24x
2
6x (x 2
+ 4x + 4) ⇒ 6x.(x +
2) 2
Fonksiyonun yerel ekstremum noktalarýnda
türevi sýfýr olduðundan;
= 0
ý
f (x) = 3x 2 − 2ax + b − 1 olup
ý
ý
f (−2) = 0 ve f (1) = 0 dýr.
Buradan x 1 = 0 ve x 2 = x 3 = −2 bulunur.
x
fý (x)
f(x)
~
−∞
0
−2
−
3(−2) 2 − 2a(−2) + b − 1 = 0
12 + 4a + b − 1 = 0
4a + b = −11 ve
+∞
+
−
7
3(1) 2 − 2a.1 + b − 1 = 0
3 − 2a + b − 1 = 0
2a − b = 2
(−∞, −2) aralýðýnda ve (−2, 0) aralýðýnda
fonksiyon azalan olup −2 noktasýnda
ý
f (−2) = 0 olduðu halde bu noktada türevin
iþaretinde bir deðiþiklik olmadýðý için yerel
ekstremum yoktur.
4a + b = −11
2a − b = 2
a = −
220
3
2
buradan,
ve b = −5 bulunur.
Artan ve Azalan Fonksiyonlar
Örnek 8
Tabloda görüldüðü gibi x = 1 apsisli noktada yerel maksimum x = −2 ve x = 3
apsisli noktalarda yerel minimum vardýr.
1 3
f(x) =
x − mx 2 − 8
3
f : R → R,
fonksiyonunun yerel ekstremum deðerlerin8
den birisinin
olduðu bilindiðine göre,
3
Ayrýca x = −1 ve x = 2 apsisli noktalarda
ikinci türevin sýfýr olduðuna ve bu noktalarýn maksimum ve minimum olmadýðýna
dikkat ediniz.
m nin deðeri kaçtýr?
Çözüm
f ý (x) =
1
. 3x 2 − 2m x dir.
3
Örnek 10
f : R → R, f(x) = x 3 + 3x 2 − 12x + 9
fonksiyonu veriliyor.
x 2 − 2mx = 0 ⇒ x(x − 2m) = 0
denkleminden x 1 = 0 ve x 2 = 2m bulunur.
ý
Buna göre, f (x) in yerel minimum noktasýný bulunuz.
Bu deðerleri denklemde yerine yazdýðýmýzda;
~
x 1 = 0 ise f(0) = −8 olduðundan bahsedilen
ekstremum deðeri deðildir.
~
x 2 = 2m ise
f(2m) =
Çözüm
ý
f (x) = 3x 2 + 6x − 12
fonksiyonunun yerel minimum noktasýný
ý
bulmalýyýz. O halde f (x) in tekrar türevini
almalýyýz.
1
8
(2m)3 − m(2m)2 − 8 =
3
3
ýý
f (x) = 6x + 6 = 0
6x = −6 ⇒ x = −1
8m3
8
4m3 32
− 4m3 = 8 +
⇒ −
=
3
3
3
3
x
fýý (x)
m3 = −8 ⇒ m3 = ( −2)3
ý
ý
O halde f (x) in yerel minimum noktasý
(−1, −15) dur.
ý
1
2
x
3
−1
2)
f(x) fonksiyonunun türevinin grafiði yukarýda verilmiþtir.
Buna göre f nin hangi x deðerinde yerel
maksimumu vardýr?
ý
Fonksiyonun türevinin grafiði verildiðine göre
bu grafikten türevin iþaretini inceleyebiliriz.
fý (x)
1
−2
+
−
3
f (x) = 0 denkleminin x 1 ,
bulunsun. Bu kökleri ikinci
yazdýðýmýzda sonuç negatif
sonuç pozitif ise minimum,
(büküm) noktasý vardýr.
+∞
+
−
ÝKÝNCÝ
TÜREVDEN
YARARLANARAK
YEREL EKSTREMUM VE DÖNÜM (BÜKÜM)
NOKTALARININ BULUNMASI
f(x) fonksiyonu (a, b) aralýðýnda türevli ve
ý
ýý
f (x) ve f (x) türevleri mevcut olsun.
Çözüm
−∞
ý
max
x 2 , x 3 kökleri
türevde yerine
ise maksimum,
sýfýr ise dönüm
f (x) = 0 denkleminin x 1 , x 2 , x 3 kökleri
bulunsun.
f(x)
min
−15
ý
f (x)
x
+
f (−1) = 3(−1) 2 + 6(−1) − 12
= 3 − 6 − 12 = −15
bulunur.
y
−2
+∞
−1
−
f (x)
⇒ m = −2 bulunur.
Örnek 9
−∞
min
221
Artan ve Azalan Fonksiyonlar
ýý
i)
f (x 1 ) > 0 ise (x 1 , f(x 1 )) noktasý minimum
noktadýr.
ii)
f (x 2 ) < 0 ise (x 2 , f(x 2 )) noktasý maksimum
noktadýr.
iii)
f (x 3 ) = 0 ise (x 3 , f(x 3 )) noktasý dönüm
(büküm) noktasýdýr.
II. yol :
f(x) in türevinin iþaretini inceleyerek de bu
soruyu çözebiliriz.
ýý
ý
f(x) = x 3 − 3x 2 + 12 ⇒ f (x) = 3x 2 − 6x = 0
x 1 = 0 ve x 2 = 2
ýý
x
fý (x)
y
2
+∞
+
−
f(0)
f(2)
max
min
minimum noktanýn ordinatý
B(x3, f(x3))
f(2) = 2 3 − 3.2 2 + 12 = 8 bulunur.
x1
x3
x2
x
Örnek 2
A(x1, f(x1))
f(x) = x 2 − 3x + x.lnx
eðrisinin ekstremum noktasýný bulunuz.
Örnek 1
Çözüm
f(x) = x 3 − 3x 2 + 12
eðrisinin minimum noktasýnýn ordinatý
nedir?
ý
f (x) = 2x − 3 + 1.lnx +
1
. x
x
2x − 2 + lnx = 0 ise x = 1 dir.
Çözüm
ýý
f (x) = 2 +
Fonksiyonun birinci türevinin kökleri maksimum ve minimum noktalarýnýn apsisleridir.
Buna göre,
1
x
ýý
⇒ f (1) = 2 +
1
> 0
1
olduðundan x = 1 apsisli nokta fonksiyonun minimum noktasýdýr.
ý
f (x) = 3x 2 − 6x ⇒ 3x 2 − 6x = 0
3x(x − 2) = 0
x 1 = 0 ve x 2 = 2
Örnek 3
Bu kökleri ikinci türevde yerine yazalým.
f : (0, 2π) → R, f(x) = sinx + cosx
fonksiyonunun ekstremum noktasýný
bulunuz.
ýý
f (x) = 6x − 6
~
+
f(x)
C(x2, f(x2))
~
0
−∞
ýý
x 1 = 0 ise f (0) = 6.0 − 6 = −6 < 0 olduðundan x 1 = 0 apsisli nokta maksimum
noktadýr.
Çözüm
ý
f (x) = cosx − sinx = 0
cosx = sinx ise tanx = 1 dir. Buradan,
ýý
x 2 = 2 ise f (2) = 6.2 − 6 = 6 > 0 olduðundan x 2 = 2 apsisli nokta minimum noktadýr.
x=
π
5π
ve x =
4
4
ýý
f (x) = − sinx − cosx = −(sinx + cosx)
Bu noktayý esas fonksiyonda yerine yazalým.
⎛ 2
2
π
π⎞
⎛π⎞
⎛
f ý ý ⎜ ⎟ = − ⎜ sin + cos ⎟ = − ⎜
+
⎜
4
4⎠
2
⎝4⎠
⎝
⎝ 2
f(x) = x 3 − 3x 2 + 12 ise
f(2) = 2 3 − 3.2 2 + 12 = 8 − 12 + 12 = 8
olduðundan x =
minimum nokta (2, 8) olup ordinatý 8 dir.
noktadýr.
222
⎞
⎟⎟ < 0
⎠
π
apsisli nokta maksimum
4
Artan ve Azalan Fonksiyonlar
⎛
2
2⎞
⎛ 5π ⎞
fý ý ⎜
−
⎟= 2 >0
⎟ = − ⎜⎜ −
2 ⎟⎠
⎝ 4 ⎠
⎝ 2
ÝKÝNCÝ TÜREVÝN GEOMETRÝK ANLAMI
BÝR EÐRÝNÝN KONKAVLIÐININ YÖNÜ
5π
olduðundan x =
apsisli nokta minimum
4
f : [a, b] → R fonksiyonu sürekli ve (a, b)
aralýðýnda birinci ve ikinci türevleri mevcut
olsun.
noktadýr.
Örnek 4
i)
f(x) = ax 3 − bx 2 − 9x + c
fonksiyonu oy eksenini 2’de kesiyor ve
A(1, −9) eðrinin dönüm noktasý olduðuna
göre, minimum noktasýný bulunuz.
ýý
(a, b) aralýðýnda f (x) > 0 ise eðrinin
çukurluðu yukarýya doðrudur.
Veya kýsaca dýþbükey (konveks) denir.
ii)
Çözüm
ýý
(a, b) aralýðýnda f (x) < 0 ise eðrinin
çukurluðunun yönü aþaðýya doðrudur.
Veya kýsaca içbükey (konkav) denir.
f(x) fonksiyonu oy eksenini (0, 2) noktasýnda kesiyorsa, c = 2 dir. A(1, −9) eðrinin
dönüm noktasý olduðuna göre bu noktalarýn apsisinde ikinci türev sýfýrdýr.
Baþka bir deyiþle çukurluk aþaðý doðru
konkav, çukurluk yukarý doðru konkav þeklinde de ifade edilebilir.
Gerçekten;
Buna göre;
ý
i)
f (x) = 3ax 2 − 2bx − 9
ýý
f (x) = 6ax − 2b
ýý
f (1) = 6a − 2b = 0 ⇒ b = 3a dýr.
y
Ayrýca A(1, −9) noktasý fonksiyonun üzerinde olduðundan f(x) de yerine yazalým.
f(x)
−9
−9
−2
−2
=
=
=
=
=
ax 3 − bx 2 − 9x + 2
a.1 3 − b.1 2 − 9 + 2
a − b − 9 + 2 ve b = 3a
a − 3a
−2a ⇒ a = 1 , b = 3
Bu
fonksiyonun
bulalým.
bulunur.
minimum
x
b
α 2 > α 1 olup
tanα 2 > tanα 1
bunu
ý
ý
f (x 2 ) > f (x 1 ) þeklinde de yazýlabilir, bu
ý
durumda; f (x) fonksiyonu deðiþkeni ile
ayný yönde deðiþtiðinden artan fonksiyondur. Dolaysýyla bunun türevi de pozitiftir,
ýý
yani f (x) > 0 dýr. O halde ikinci türevi
pozitif yapan x deðerleri için eðrinin çukurluðu yukarý doðru konveks olacaktýr.
noktasýný
ý
f (x) = 3x 2 − 6x − 9 = 0
3(x 2 − 2x − 3) = 0
+1
x2
Yukarýdaki þekilde görüldüðü gibi çukurluk
yukarýya doðru olan bir eðri üzerinde
apsisi daha büyük olan bir noktadaki eðim
açýsý daha büyüktür.
Buna göre;
f(x) = x 3 − 3x 2 − 9x + 2
α2
α1
a x1
−3
3.(x + 1).(x − 3) = 0 ise x = −1 ve x = 3
bulunur. Bunlarý ikinci türevde yerine yazalým.
ii)
y
ýý
f (x) = 6x − 6
ýý
f (−1) = 6(−1) − 6 = −12 < 0
olduðundan (−1, f(−1)) noktasý maksimum
noktadýr.
ýý
f (3) = 6.3 − 6 = 12 > 0 olduðundan
(3, f(3)) noktasý da f(x) in minimum noktasýdýr.
α2
223
α1
0
a x1
x2
b
x
Artan ve Azalan Fonksiyonlar
Uyarý (3) :
ý
ýý
ýýý
f (a) = 0 , f (a) = 0 , f (a) = 0 olmasý hallerinde x = a için sýfýr olmayan ilk türev
bulununcaya kadar türev almaya devam
edilir. Bu taktirde (a, f(a) ) noktasý; sýfýr
olmayan ilk türevin derecesi tek ise bir
büküm noktasý, çift ise ekstremum noktasýdýr.
Yukarýdaki þekilde görüldüðü gibi çukurluk
aþaðýya doðru (kýsaca konkav) olan bir
eðri üzerinde apsisi daha büyük olan noktadaki eðim açýsý daha küçüktür.
Buna göre;
α 2 < α 1 ise tanα 2 < tanα 1 ve bunu
ý
ý
f (x 2 ) < f (x 1 ) þeklinde de gösterebiliriz. O
ý
halde f (x) fonksiyonu deðiþkeni ile ters
yönde deðiþmekte olduðundan azalan
fonksiyondur. Dolaysýyla bunun türevi de
ýý
negatiftir, yani f (x) < 0 dýr.
Örnek 1
f(x) =
O halde ikinci türevi negatif yapan x deðeri
için eðrinin çukurluðu aþaðýya doðru
(konkav) olacaktýr.
1 4
.x − 6x 2 + 8x − 15
4
eðrisinin aþaðý ve yukarý doðru konkav
olduðu aralýklarý bulunuz.
Çözüm
Uyarý (1) :
f(x) fonksiyonu bir A(x o , y o ) noktasýndaki
teðetinin üst tarafýnda kalýyorsa çukurluk
yukarý doðru (konveks); teðetinin alt
tarafýnda kalýyorsa çukurluk aþaðý doðru
(konkav) adýný alýr.
f(x) fonksiyonunun ikinci türevinin iþaretini
inceleyelim.
ý
f (x) = x 3 − 12x + 8
ýý
f (x) = 3x 2 − 12 = 3(x 2 − 4) = 0
x2 = 4 ⇒ x1 = 2 ,
y
x
teðet
ýý
f (x)
A
−∞
x 2 = −2
2
−2
+
+∞
+
−
ýý
x1
0
x0
f′′(x) < 0
x2
f′′(x) > 0
ý
,
f (x 2 ) > 0
ýý
,
f (x 2 ) > 0
,
f (x o ) = 0 dýr.
f (x 1 ) > 0
f (x 1 ) < 0
ý
f (x o ) ≠ 0
x < −2 ve x > 2 için f (x) > 0 olduðundan eðri yukarý doðru konkav −2 < x < 2
ýý
için f (x) < 0 olduðundan eðri aþaðý doðru
konkavdýr.
x
ý
Örnek 2
ýý
f(x) = e x
eðrisinin konkavlýðýný inceleyiniz.
ýý
Çözüm
y
Uyarý (2) :
Sürekli bir f(x) fonksiyonunun çukurluðunun yön deðiþtirdiði noktaya fonksiyonunun dönüm (büküm) noktasý denir.
1
x
y = f(x) denklemi ile verilen bir eðri üzerindeki bir (a, f(a) ) noktasýnýn büküm
(dönüm) noktasý olmasý için;
ýý
ýýý
f (a) = 0 ve f (a) ≠ 0
y = ex
ý
ýý
f (x) = e x ve f (x) = e x > 0 olduðundan ve
þekilde de görüldüðü gibi ∀x ∈ R için
eðrinin konkavlýðý yukarý doðrudur.
olmalýdýr.
224
Artan ve Azalan Fonksiyonlar
ýý
Örnek 3
f (1 − h) = 20(1 − h − 1) 3 = −20h 3 < 0
f : R → R, f(x) = 1 − x 2
eðrisinin konkavlýðýný inceleyiniz.
Çözüm
ýý
f (1 + h) = 20(1 + h − 1) 3 = 20h 3 > 0
ýý
x = 1 in saðýnda ve solunda f (x) iþaret
deðiþtirdiðinden x = 1 apsisli nokta dönüm
(büküm) noktasýdýr.
y
1
Örnek 6
1
−1
ý
1
f(x) = x 2 +
x
x
fonksiyonunun dönüm (büküm) noktasýný
bulunuz.
ýý
f (x) = −2x ve f (x) = −2 < 0 olduðundan
ve þekilde de görüldüðü gibi ∀x ∈ R için
çukurluðun yönü aþaðý doðrudur.
Çözüm
2
Örnek 4
x3
1
ý
f (x) = 2x −
x3
3x 2
f : R → R, f(x) =
−
+ 3x − 5
eðrisinin konkavlýðýný inceleyip büküm
noktasýný bulunuz.
, f (x) = 2 +
2
x3
= 0 ise,
= −2 ise x 3 = −1 ⇒ x = −1 dir.
ýýý
f (x) = −
Çözüm
ýý
x2
6
x4
⇒
ýýý
f (−1) ≠ 0 olduðundan
x = −1 apsisli nokta f(x) in dönüm (büküm)
noktasýdýr.
ý
f (x) = 3x 2 − 6x + 3
ýý
f (x) = 6x − 6 = 6(x − 1) = 0 ise x = 1
ýýý
f (x) = 6 ≠ 0
x
fýý (x)
Örnek 7
bu durumda;
1
−∞
f(x) = x 3 + 3x 2 + mx − 4
eðrisinin dönüm (büküm) noktasý y = x + 1
doðrusu üzerinde ise, m deðeri kaçtýr?
+∞
+
−
Çözüm
Önce fonksiyonun dönüm noktasýný bulalým. Bu noktada ikinci türev sýfýr olup bu
nokta y = x + 1 doðrusu üzerinde olduðundan bu doðru denklemini saðlar.
x < 1 için çukurluðun yönü aþaðý doðru
x > 1 için çukurluðun yönü yukarý doðru
x = 1 noktasý f(x) in dönüm noktasýdýr.
ý
x = −1 ise
ýý
y = x + 1 den
f (x) = 3x2 + 6x + m
f (x) = 6x + 6 = 0
Örnek 5
f : R → R, f(x) = 2 + (x − 1) 5
eðrisinin büküm (dönüm)
bulunuz.
x = −1
noktasýný
y = 0 dýr.
Dönüm noktasý A(−1, 0) noktasýdýr. Bu noktayý f(x) de yerine koyalým.
Çözüm
0 = (−1) 3 + 3(−1) 2 + m(−1) − 4
ý
ýý
f (x) = 5(x − 1) 4 , f (x) = 20(x − 1) 3 ,
ýýý
f (x) = 60(x −
ýý
1) 2
−1 + 3 − m − 4 = 0 ⇒ m = −2 bulunur.
olup x = 1 için
Örnek 8
ýýý
f (1) = 0 ve f (1) = 0 olduðundan x = 1 in
f(x) = x 3 − ax 2 + bx − 4
eðrisinin x = 1 apsisli noktasý dönüm
(büküm) noktasý olup, bu noktadan çizilen
teðet 2x − 2y + 3 = 0 doðrusuna paralel
olduðuna göre, a + b nin deðeri kaçtýr?
büküm noktasý olup olmadýðý hakkýnda
birþey söylenemez.
ýý
x = 1 de f (x) in iþaret deðiþtirip deðiþtirmediðini araþtýralým.
225
Artan ve Azalan Fonksiyonlar
Çözüm
Çözüm
x = 1 , f nin dönüm noktasý olduðuna göre;
ýý
x.y çarpýmýný tek deðiþkenli fonksiyon
haline getirip türevini alýp sýfýra eþitleyerek
ekstremum noktalarýný bulalým.
ýý
f(x) = x.y = x(12 − 2x) = 12x − 2x 2
ý
f (x) = 3x 2 − 2ax + b
f (x) = 6x − 2a
f (1) = 6.1 − 2a = 0 ⇒ a = 3
ý
f (x) = 12 − 4x = 0 ⇒ x = 3
x = 1 apsisli noktadan çizilen teðet
x = 3 ise 2.3 + y = 12 ⇒ y = 6 bulunur.
2x−2y + 3 = 0 doðrusuna paralel olduðuna göre eðimleri eþittir.
ý
f (1) =
3(1) 2
O halde x . y = 3 . 6 = 18 en büyük deðer
olarak bulunur.
− 2.3.1 + b = 3 − 6 + b = −3 + b
2x − 2y + 3 = 0 doðrusunun eðimi 1 dir.
Örnek 2
O halde bu eðimleri eþitleyelim.
−3 + b = 1
b = 4
x, y ∈ R + ve x + y = 24 ise
x 2 .y çarpýmýnýn en büyük deðeri alabilmesi
için x’in deðeri kaç olmalýdýr?
olup,
a + b = 3 + 4 = 7
bulunur.
bulunur.
Çözüm
x 2 .y çarpýmýný tek deðiþkene baðlý olarak
yazalým ve türevini alýp sýfýra eþitleyelim.
MAKSÝMUM VE MÝNÝMUM
PROBLEMLERÝ
f(x) = x 2 .y = x 2 (24 − x) = 24x 2 − x 3
ý
f(x) = 24x 2 − x 3 ⇒ f (x) = 48x − 3x 2 = 0
3x.(16 − x) = 0 ⇒ x = 0 ve x = 16 bulunur.
Deðiþken bir ifadenin maksimum ve minimum deðerleri, uygulama alaný çok olan
deðerlerdir. Bir merminin ulaþabileceði en
büyük yüksekliðin bulunmasý, verilen bir
hacimde depo yapýlabilmesi için minimum
miktarda malzemeye ihtiyaç duyulmasý, bir
küre içine yerleþtirilecek en büyük hacimli
silindirin boyutlarýnýn bulunmasý gibi sorulara verilecek cevaplar bu gibi problemlerin
çözümü ile elde edilecektir.
x = 0 çarpýmý maksimum yapamayacaðýndan x = 16 dýr.
Örnek 3
f(x) = x 2 − 2ax + 13
fonksiyonunun minimum deðerinin −3 olmasý için a’nýn pozitif deðeri kaçtýr?
Çözüm
ý
f (x) = 2x − 2a
2x − 2a = 0 ⇒ x = a
Maksimum ve minimum problemlerini çözebilmek için evvela maksimum ve minimum
olmasý istenilen büyüklüðün yalnýz bir
deðiþken cinsinden ifade edilip, sonra
bunun türevi sýfýra eþitlenerek elde edilen
denklem çözülür. Bu denklemin kökleri
esas fonksiyonda yerlerine yazýlarak maksimum ve minimum deðerleri bulunur.
Bunu f(x) fonksiyonunda yerine yazarak
minimum deðere eþitleyelim.
f(x) = a 2 − 2a.a + 13 = −3
−a 2 = −16
a 2 = 16 ⇒ a = 4 bulunur.
Örnek 4
Bir dikdörtgenin üç kenarýnýn uzunluklarý
toplamý 36 cm ise, alaný en çok kaç cm 2
olur?
Örnek 1
x, y ∈ R + ve 2x + y = 12 ise
x.y çarpýmýnýn en büyük deðeri kaçtýr?
Çözüm
Dikdörtgenin üç kenarýnýn toplamý 36 ise,
2x + y = 36 dýr.
226
Artan ve Azalan Fonksiyonlar
A(x) = x.y = x(36 − 2x) = 36x − 2x 2
ý
A (x) = 36 − 4x = 0 ⇒ x = 9
y = 2a2 − x 2 dir.
x 2 + y 2 = 2a 2 ⇒
x = 9 ise 2.9 + y = 36 ⇒ y = 18
A(ABC) = f(x) =
Alaný : x.y = 9.18 = 162 cm 2 olarak
bulunur.
fý (x) =
1
x. 2a 2 − x 2
2
1
−2x
x
. 2a2 − x 2 +
. =0
2
2
2
2
2 2a − x
1
x2
2a2 − x 2 =
2
2 2a2 − x 2
Örnek 5
Toplamlarý 10 olan iki pozitif tamsayýnýn
kareleri toplamý en fazla kaç olur?
2a 2 − x 2 = x 2 ⇒ x 2 = a 2 ise x = a dýr.
Çözüm
1
1
a2
.a. 2a 2 − a 2 = a.a =
cm 2
2
2
2
bulunur.
f(a) =
Bu sayýlardan birine x dersek diðeri 10 − x
olur. Kareleri toplamýný bir fonksiyon þeklinde ifade edecek olursak,
f(x) = x 2 + (10 − x) 2 = x 2 + 10 2 − 20x + x 2
f(x) = 2x 2 − 20x + 100
f : [1, 9] → R þeklinde tanýmlanan f(x)
fonksiyonun maksimum deðerini bulmak
istiyoruz, fonksiyon bir parabol belirtir.
Örnek 7
Bir kenarý x ekseni diðer kenarý y ekseni
üzerinde ve bir köþesi y = 4 − x 2 eðrisi
üzerinde deðiþen dikdörtgenlerin en
büyüðünün alaný kaç cm 2 dir?
ý
f (x) = 4x − 20 = 0 ⇒ x = 5
x
5
−∞
yý
+∞
+
−
Çözüm
y
f(1) = 1 2 + 9 2 = 82
f(5) = 5 2 + 5 2 = 50
f(9) = 9 2 + 1 2 = 82
x
Örnek 6
y′
Hipotenüs uzunluðu añ2 olan bir dik
üçgenin alaný en fazla kaç cm 2 olur?
Çözüm
4 − x2
x
2
2
3
3
+
−
+∞
−
y
min
max
3
B
⎛ 2 ⎞
2 ⎛ 2 ⎞
8
8
S⎜
−⎜
−
⎟=4.
⎟ =
3 ⎝ 3⎠
3 3 3
⎝ 3⎠
a 2
y
1
x . y dir.
2
−
−∞
A
Üçgenin dik kenarlarýna x
ve y diyelim. Üçgenin alaný,
4
4
2
x 2 = ise x = ±
3
3
O halde sayýlarýn kareleri toplamý en fazla
82 olur.
A(ABC) =
y
Alan fonksiyonu;
S(x) = x . (4 − x 2 )
S(x) = 4x − x 3
ý
S (x) = 4 − 3x 2 = 0
min
x
=
C
Pisagordan,
227
24 − 8
3 3
=
16
3 3
=
16 3
9
bulunur.
x
Artan ve Azalan Fonksiyonlar
Örnek 8
Çözüm
A
Bir küre içine yerleþtirilebilen maksimum
hacimli silindirin yarýçapýný ve yüksekliðini bulunuz.
F
D x
h
Çözüm
y
|AB| 2 = |AC| 2 − |BC| 2
D
|AB| 2 = (2R) 2 − x 2
C
E
B
C
x
|AB| 2 = 4R 2 − x 2
4R2 − x 2
|AB| =
AB
r=
2
=
Silindirin deðiþken olan taban yarýçapýna
x, yüksekliðine de y diyelim. Bu silindirin
hacmi
B
1
. 4R2 − x 2
2
V = π . x 2 . y dir.
⎛ 4R2 − x 2
V = π r2 . h = π ⎜
⎜
2
⎝
V=π
r
A
AEC üçgeni
olduðundan
2
⎞
⎟ .x
⎟
⎠
x h −y
=
r
h
π
4R2 − x 2
. x = (4R2 x − x 3 )
4
4
Vý (x) =
π
(4R 2 − 3x 2 )
4
4R = 3x
ile
x=
⇒
ADF
üçgeni
benzer
r
(h − y)
h
x in bu deðerini V hacim formülünde yerine
yazalým.
2
⎛r⎞
V = π . x 2 .y = π . ⎜ ⎟ .(h − y)2 .y
⎝h⎠
π
π
(4R2 − 3x 2 ) = 0 , ≠ 0 olduðundan
4
4
2
r
x
R
Vý (y) =
2
π r2
4R2
2R
⇒ x=±
x =
3
3
2
h2
Silindirin yüksekliði x = h =
2R
3
bulunur.
=
r=
.[ 2(h − y).( −1).y + 1.(h − y) 2]
.(h − y)[(h − y − 2y)] = 0 ise
V (y)
2
h
3
h
y
ý
1
1
4R
= . 4R2 − x 2 = . 4R2 −
r=
2
2
2
3
h2
y = h ve y =
Silindirin yarýçapý
AB
π r2
+
+
−
max
2 2R
1 8R2
=
.
2
3
2 3
h
3
min
h
yani maksimum hacimdeki silindirin
3
h
yüksekliði
dür.
3
y=
2
R bulunur.
3
Örnek 10
Örnek 9
A(3, 4) noktasýndan çizilen doðrular ve
koordinat eksenleri ile birinci bölgede
oluþan üçgenlerden alaný en küçük olanýn
alaný kaç br 2 dir?
Yarýçapý r yüksekliði h olan bir dik koni
içine yerleþtirilmiþ maksimum hacimdeki
silindirin yüksekliðini bulunuz.
228
Artan ve Azalan Fonksiyonlar
Çözüm
Bu durumda x = 3 de minimum deðerini
aldýðýndan üçgenin en küçük alaný;
y
B
18
+ 2x
x
18
+ 2.3
f(3) = 12 +
3
A(OBC) = f(x) = 12 +
y
A(3, 4)
E
4
0
3
D
x
C
f(3) = 12 + 6 + 6 = 24 br 2 bulunur.
x
Örnek 11
Meydana gelen üçgenin alaný,
Eþkenar bir üçgenin içine çizilebilen ve
alaný maksimum olan dikdörtgenin
boyutlarýný bulunuz.
1
A(OBC) =
(3 + x).(4 + y)
2
Çözüm
ABE üçgeni ile ADC üçgeni benzer üçgenlerdir.
Buna göre;
A
y 3
=
⇒ x . y = 12
4 x
K
G
F
y
1
A(OBC) = .(3 + x).(4 + y)
2
B
1
(3y + 4x)
2
f(x) = 12 +
1 12
+ 4x)
(3.
2
x
AH = h =
AK =
f ý (x) = −
2=
x2
18
x
f ý ý (x) =
f ý ý (3) =
+2 = 0
33
f ý ý ( −3) =
a 3
−y
2
⇒ a 3 − 2y = 2 3x
3
36
a 3
2
AKF üçgeni ile AHC üçgenleri benzer
olduðundan
a 3
−y
AK
KF
x
=
⇒ 2
=
a
AH
HC
a 3
2
2
36
x
C
x ve y uzunluklarýnýn deðiþken olduðunu
görün.
ise x 2 = 9 ⇒ x = ± 3
2
E
HE = KF = x diye lim.
18
+ 2x , fonksiyonu bulunur.
f(x) = 12 +
x
18
x
ABC eþkenar üçgenin bir kenarý a olsun.
Yüksekliði,
1
[12 + 3y + 4x + 12 ]
2
f(x) = 12 +
H
a/2
1
= [12 + 3y + 4x + xy]
2
=
D
⇒ 2y = a 3 − 2 3x
DEFG dikdörtgeninin alaný
> 0 olduðundan minimum,
Alan = 2x . y = x . 2y
36
3
( −3)
A(x) = x . (añ3 − 2ñ3 . x) = añ3x − 2ñ3x 2
< 0 olduðundan maksimum
ý
A (x) = añ3 − 4ñ3x = 0
deðer alýr.
añ3 = 4ñ3x ⇒ a = 4x
229
Artan ve Azalan Fonksiyonlar
y=
3
(a − 2x) olduðundan
2
y=
3
2
Örnek 13
a⎞
3 a a 3
⎛
. =
⎜a − 2 . ⎟ =
4⎠
2 2
4
⎝
ACE doðrusal
1
[AB] ⊥ [BC]
B
C
[CD] ⊥ [DE]
Dikdörtgenin boyutlarý
x=
A
Yandaki þekilde,
[BC] // [DE]
|AB|= 1
a
a 3
ve y =
bulunur.
4
4
D
|DE|= 8 dir.
θ
8
E
Buna göre tanθ nýn hangi deðeri için,
|AC|+|CE| toplamý en küçüktür?
Örnek 12
Üst kýsmý x yarýçaplý bir yarým daire þeklinde ve esas kýsmý 2x ve y boyutlu bir
dikdörtgen þeklinde olan bir pencerenin
çevresi sabit bir a sayýsýna eþittir.
Çözüm
A
Δ
A B C de
Buna göre pencerenin alanýnýn maksimum olabilmesi için pencerenin boyutlarý ne olmalýdýr?
x=
x
1
1
sin θ =
x
θ
B
1
sin θ
y
Δ
CDE de
Çözüm
Pencerenin çevresi
πx + 2x + 2y = a dýr.
2y = a − πx − 2x
y=
y
1 2
πx + 2x .y dir.
2
A(x) =
1
π x 2 + x . [a − πx − 2x]
2
=
f ý ( θ) =
y=
1 ⎡ aπ + 4a − aπ − 2a ⎤
⎥
2 ⎢⎣
π+4
⎦
a
π+4
3
c os θ
+
8.sin θ
c os 2 θ
=
=0
c os θ
sin2 θ
=
1
8
3
1
⎛ 1⎞
tan3 θ = ⎜ ⎟ ise tan θ =
2
2
⎝ ⎠
bulunur.
1
2a
a
.
=
2 π+4 π+4
O halde pencerenin boyutlar ý
2a
a
ve y =
π+4
π+4
sin θ
sin3 θ
=
2x =
2
8.sin3 θ = c os 3 θ
1
y = [ a − x( π + 2)]
2
a( π + 2) ⎤
1 ⎡
. a−
π + 4 ⎥⎦
2 ⎢⎣
− c os θ
c os2 θ
a − πx − 4x = 0
y=
1
8
+
sin θ c os θ
8.sin θ
Aý (x) = πx + a − 2πx − 4x
θ
8
8
c os θ
f( θ) = x + y =
2x
1
π x 2 + ax − πx 2 − 2x 2 ]
2
a = x( π + 4) ⇒ x =
D
8
c os θ =
y
x
Alan =
C
yani x = y dir.
230
E
ALIÞTIRMALAR 2
1.
Artan ve Azalan Fonksiyonlar
6.
f(x) = x3 − 3x2 − 9x + 7
fonksiyonunun artan ve azalan olduðu aralýklarý bulunuz.
f(x) = x3 + 3x2 − 45x + 5
fonksiyonunun azalan olduðu aralýktaki tamsayýlarýn toplamý kaçtýr?
Cevap : (−∞, −1) ∪ (3, +∞) artan
(−1, 3) azalan
Cevap : −7
7. f(x) =
2.
mx − 7
x +1
fonksiyonu ∀x ∈ R − {−1} için
artan ise m nin alacaðý deðerleri bulunuz.
f(x) = x3 − mx2 + 3x + 7
fonksiyonu m nin hangi deðeri için monoton
artandýr?
Cevap : m > −7
Cevap : −3 < m < 3
8.
f(x) = sinx + cosx
fonksiyonunun maksimum deðeri kaçtýr?
Cevap : ñ2
3.
x3
3x2
f(x) =
−
+5
fonksiyonunun yerel ekstremum noktalarýný
bulunuz.
Cevap : A(0, 5) max. nokta
B(2, 1) min. nokta
9.
f(x) = x4 + ax3 − bx + 3
fonksiyonunun iki tane dönüm noktasý vardýr.
Bu noktalarýn apsisler toplamý 3 ise a kaçtýr?
Cevap : −6
4.
f(x) = ax2 + 2x + b
fonksiyonunun A(−1, 2) noktasý minimum noktasý
ise a+b toplamý kaçtýr?
10. f(x) =
x 2 − mx
fonksiyonunun yerel ekstremum
x +1
noktalarýnýn apsisleri x1 ve x2 olmak üzere,
2x1 − x2 = 5 ise m kaçtýr?
Cevap : 4
Cevap : 3
5.
f(x) = x4 − (m − 1)x3 + ax2 + b
eðrisinin yerel ekstremum noktalarýnýn apsisleri
toplamý 9 ise m nin deðeri kaçtýr?
11.
Cevap : 13
f(x) = x3 − 3x2 + 4x + 3
fonksiyonunun dönüm noktasýndan çizilen
teðetin denklemini bulunuz.
Cevap : y = x + 4
231
ALIÞTIRMALAR 2
12.
Artan ve Azalan Fonksiyonlar
y
16.
ý
y = f (x)
4
−1
1
3
5
f(x) = x 2 −
9
2
parabolü üzerindeki herhangi bir nokta ile
orjin arasýndaki en kýsa uzaklýk kaç birimdir?
x
Cevap :
17
2
Yukarýda f(x) in türevinin grafiði verilmiþtir.
Buna göre, f(x) in yerel maksimum noktasýnýn
apsisi kaçtýr?
Cevap : 3
17. y = x2 parabolünün 2x − y − 4 = 0 doðrusuna
en kýsa uzaklýðý kaç birimdir?
Cevap :
13.
x2 − 2mx + m + 4 = 0
denkleminin köklerinin kareleri toplamýnýn minimum olmasý için m kaç olmalýdýr?
1
Cevap :
4
3
5
18. y = x2 + 1 parabolünün A(5, 0) noktasýna
en kýsa uzaklýðý kaç birimdir?
Cevap : 2ñ5
14. A(3x, 2) ve B(2x, x−4) noktalarý arasýndaki uzaklýðýn en kýsa olabilmesi için x kaç olmalýdýr?
Cevap : 3
19. f(x) = x3 − mx2 + 2x + 3 fonksiyonunun konkav
(iç bükey) olduðu aralýk (−∞, 2) ise m deðeri
nedir?
15.
Cevap : 6
y
d
4
C
A
5
0
B
x
20. y2 = 9x parabolü ve x = 8 doðrusu ile kesilerek, bir kenarý x = 8 doðrusu üzerinde iki köþesi parabol üzerinde deðiþen dikdörtgenlerin
en büyük olanýnýn alaný kaç birim karedir?
Yukarýdaki þekilde ABOC dikdörtgeninin A köþesi
d doðrusu üzerinde deðiþmektedir.
Buna göre ABOC dörtgeninin alaný en fazla
kaç br2 olur?
Cevap : 5
Cevap : 64 6
3
232
TEST 2
1.
Artan ve Azalan Fonksiyonlar
6. Aþaðýdaki fonksiyonlardan hangisi daima
f(x) = x3 − x2 − 5x + 4
fonksiyonunun azalan olduðu aralýk aþaðýdakilerden hangisidir?
5
A) −1 < x <
3
B) 3 < x < 1
D) 0 < x < ∞
artandýr?
A) f(x) = −2
B) f(x) = x
D) f(x) = −2x + 3
C) 0 < x < ∞
C) f(x) = e
E) f(x) = 5 − x
E) −∞ < x < −1
7. f(x) fonksiyonu (a, b) aralýðýnda pozitif deðerli
2. f(x) =
ve artan bir fonksiyon olduðuna göre aþaðýdaki
fonksiyonlardan hangisi ayný aralýkta artandýr?
x
fonksiyonunun artan olduðu aralýk
ln x
aþaðýdakilerden hangisidir? (x ≠ 1, x ∈
A) (0, e)
B) (1, e)
D) (−∞, 0)
A) −f(x)
R+)
C) f 3(x)
B) 3 − f(x)
1
f(x)
D)
C) (e, +∞)
1
E)
2
f (x)
E) (−e, 1)
8. (a, b) aralýðýnda ∀x ∈ (a, b) için türevi pozitif olan fonksiyon aþaðýdakilerden hangisidir?
y
A)
3.
f(x) = x3 + bx2 + 3x + m
fonksiyonu daima artan olduðuna göre b’nin
alacaðý deðerler aþaðýdakilerden hangisidir?
A) −1 < b < 1
B) −2 < b < 3
D) −3 < b < 3
y
B)
x
a
a
b
y
D)
C) −3 < b < 1
y
x
b
E)
E) 0 < b < 3
x
a
b
y
x
a
x
b
a
y
9.
4. f : R − {2} → R olmak üzere,
f(x) =
C)
2x + m
fonksiyonunun daima artan olmax −2
f(x)
2
3
x
4
−2
sý için m aþaðýdakilerden hangisi olmalýdýr?
b
−3
A) m < −4
B) m < 0
D) −2 < m < 4
C) 4 < m
Yukarýda tepe noktasý T(2, −3) olan parabol
verilmiþtir. Buna göre aþaðýdakilerden hangisi
doðrudur?
E) 0 < m < 4
ý
A) f (−3) > 0
ý
B) f(0) > 0
ý
C) f (2) = 0
ý
D) f (3) < 0
E) f (4) = 0
5. Aþaðýdaki fonksiyonlardan hangisi daima
azalandýr?
10.
A) f(x) = −4
B) f(x) = 3x − 2
C) f(x) = logx
D) f(x) = −3x + 2
E) f(x) =
3x
f(x) = x . lnx − 2x
eðrisinin yerel ektremum noktasýnýn apsisi
kaçtýr?
A) 0
+1
233
B) 1
C)
1
2
D)
1
e
E) e
Artan ve Azalan Fonksiyonlar
TEST 2
17.
11. f(x) = x2 − ax + b fonksiyonunun yerel minimum
y
noktasý (2, −5) ise a+b toplamý kaçtýr?
A) 2
B) 3
C) 4
D) 5
E) 6
−2
−3
12.
f(x) =
1 3
x − x 2 − 3x + 4
3
fonksiyonu
doðrudur?
A)
B)
C)
D)
E)
için
1
x
2
Yukarýda f(x) fonksiyonunun grafiði verilmiþtir.
Buna göre aþaðýdakilerden hangisi doðrudur?
aþaðýdakilerden
hangisi
ýý
ýý
A) f (1) = 0
ý
C) f (−2) = 0
ý
D) f (0) < 0
−∞ < x < 3 aralýðýnda fonksiyon artandýr.
x = 2 de yerel minimum vardýr.
x = −1 de yerel maksimum vardýr.
−∞ < x < −1 aralýðýnda fonksiyon azalandýr.
1 < x < 3 aralýðýnda fonksiyon artandýr.
ýý
B) f (−2) < 0
E) f (−3) > 0
y
18.
y = ñx
A(0, 3)
P
13. [a, b] aralýðýnda tanýmlý f(x) fonksiyonu için
x
ý
f (x) < 0 olduðuna göre aþaðýdakilerden hangisi
daima doðrudur?
A) f(b) < f(x) < f(a)
B) f(a) < f(x) < f(b)
Yukarýda A(0, 3) noktasýnýn y = ñx eðrisine en
yakýn noktasý P ise |AP| uzunluðu kaçtýr?
C) f(a) < f(x)
D) f(a) < f(b)
A) 2
B) 3
C) 2ñ2
D) ñ5
E) ñ6
E) f(a) = 0
14.
f(x) = x3 − 3x2 + 5x − 7
fonksiyonunun dönüm noktasý aþaðýdakilerden hangisidir?
A) (−2, 4)
B) (1, −4)
D) (1, 3)
15.
19. x ∈ R olmak üzere (4 − x).(2x + 3) çarpýmýnýn
alacaðý en büyük deðer kaçtýr?
A) −4
C) (1, 4)
B) −2
C)
11
2
D)
55
4
E)
121
8
E) (4, −1)
f(x) = x3 − (m − 2)x2 + nx + 10
fonksiyonunun dönüm (büküm) noktasý (2, 0) ise
m+n toplamý kaçtýr?
20.
y
y = x2
y=6
A) 7
B) 8
C) 10
D) 11
E) 12
x
16. Bir iþ yerinde bir günde üretilen x tane birim malýn
maliyeti f(x) = x2 + 2x + 40 lira olduðu bilinmektedir. Birim malýn satýþ fiyatý 50 − x lira
olduðuna göre günlük kârýn maksimum olabilmesi için bir günde kaç birim mal üretilmelidir?
Yukarýdaki þekilde y = x2 parabolünün içine
bir kenarý y = 6 doðrusu diðer kenarý y ekseni
üzerinde ve bir köþesi de y = x2 parabolü
üzerinde deðiþen bir dikdörtgen yerleþtirilmiþtir.
A) 8
A) 6ñ3
B) 10
C) 12
D) 13
Bu dikdörtgenin maksimum alaný kaç br2 dir?
E) 14
B) 6ñ2
C) 2ñ5
D) 5ñ2
E) 4ñ2
Cevaplar: 1- A 2-C 3-D 4-A 5-D 6-B 7-C 8-D 9-C 10-E 11-B 12-C 13- A 14-B 15-D 16-C 17-A 18-D 19-E 20-E
234