AKIŞ REJİMİNİN BELİRLENMESİ
1. Deneyin Amacı
Kimyasal proseslerde, akışkanlar borulardan, kanallardan ve prosesin yürütüldüğü donanımdan
geçmek zorundadır. Bu deneyde dairesel kesitli borularda sıkıştırılamayan bir akışkanın laminer
ve türbülent akış rejiminin belirlenmesi ve laminer akışta boru merkezindeki hızın ve ortalama
hızın ölçülerek teorik oranla karşılaştırılması amaçlanmıştır.
2. Deney Teorisi
2.1. Kuramsal Temeller
Laminer Akış: Akışkanın birbirine paralel ve düzgün tabakalar halinde aktığı akış biçimidir.
Türbülent Akış: Akışkanın düzensiz, çapraz akışlar ve girdaplar halindeki akışıdır.
Reynolds Sayısı: Reynolds, akışın bir rejimden diğer rejime dönüştüğü şartları incelemiş ve
laminer akışın türbülent akışa dönüştüğü kritik hızın dört büyüklüğe bağlı olduğunu belirlemiştir.
Bu büyüklükler; akışkanın içinden aktığı boru çapı (D), akışkanın viskozitesi
yoğunluğu
,
ve ortalama çizgisel hızı ( ̅ ) olup boyutsuz tek bir grup içinde birleştirilebilir.
Akışın şeklinde olabilecek bir değişim bu grubun belirli bir değerinde olmalıdır.
̅
̅
Reynolds sayısının büyüklüğü, kullanılan birimlerin birbirine uygun olması şartıyla birimlere
bağlı değildir. Laminer akıştan türbülent akışa geçiş bir Re sayısı aralığında olabilir. Kapalı
dairesel kesitli borularda laminer akışta çoğunlukla Re sayısı yaklaşık olarak 2100’den küçükür.
Normal akış şartlarında Re sayısının yaklaşık olarak 4000’den büyük değerlerinde akış
türbülenttir. Re sayısının 2100 - 4000 arasındaki değerlerinde giriş şartlarına bağlı olarak akış
şekli ne tam laminer ne de türbülent olmayıp, bu aralıktaki akış genellikle geçiş bölgesi diye
adlandırılır.
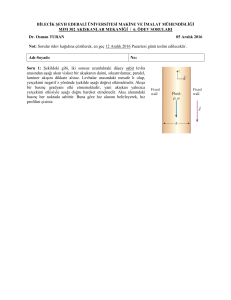
Borusal bir akışta akışın ve hız profilinin gelişmesi Şekil 1’de gösterilmektedir. Bu şekilde
dairesel bir boruya giren akışkan, duvarlarla temas ettiğinde kaymazlık şartından dolayı,
duvarlarda hız sıfır olmakta ve duvarlardan boru merkezine doğru uzaklaştıkça hız artmaktadır.
Sonuç olarak borunun herhangi bir kesitinde r yönünde değişen bir hız profili oluşmaktadır. Hız
1
profili, yüzeye dik yönde yerel hızların mesafe ile değişimini veren grafiktir. Duvarla akış
arasında yerel hızların değiştiği bölgeye sınır tabakası adı verilir.
Şekil 1. Dairesel kesitli bir boruda hız profilleri ve hızın gelişmesi.
Boru içinde akış yönünde belirli bir mesafeye kadar, hız değişimi merkeze ulaşıncaya kadar, hız
profillerinin şekli x-yönünde değişir. Daha sonra hız profillerinin şekli sabit kalır ve akış
yönünde değişmez. Hız profillerinin x-yönünde değiştiği bölgeye, hidrodinamik olarak
gelişmekte olan akış, sabit kaldığı bölgeye ise tam gelişmiş akış denir.
Laminer akış için hidrodinamik giriş bölgesinin uzunluğu aşağıdaki eşitlikten hesaplanır:
(2)
Türbülent akış için ise tam gelişmekte olan bölgenin uzunluğu yaklaşık 10 boru çapı uzunluğu
olarak alınır.
2.2. Borularda Akış Rejimleri
Düzgün bir boruda laminer ve türbülent akışla akan Newtonian bir akışkan için tipik bir hız
dağılımı Şekil 2’de gösterilmektedir. Şekilde aynı zamanda aynı türbülent akışta hız bölgeleri de
gösterilmektedir. Türbülent akış için dağılım eğrisinin, laminer akış için olandan daha geniş bir
parabol olduğu görülüyor. Aynı zamanda maksimum hız ve ortalama hız arasındaki fark daha
küçüktür.
2
Şekil 2. Tam gelişmiş laminer ve türbülent akışta radyal yönde hız dağılım profili.
Laminer akışta borunun tüm kesit alanında akış rejimi lanimerdir ve katı yüzeye yakın çok ince
bir tabakada akış çok yavaştır ve akış rejimi lanimerdir. Bu tabakaya girdap (edi) nadiren ulaşır.
Belirli bir kalınlığı olan ve içerisinde sürekli olarak girdap bulunmayan laminer özelliğe sahip bu
tabakaya viskoz alt tabaka denir. Viskoz alt tabaka akış kesitinin sadece küçük bir bölümünü
kaplar. Viskoz alt tabaka üzerinde değişik büyüklükteki girdapların etkisinden, dolayı herhangi
bir noktada viskoz alt tabaka kalınlığı zamanla değişir. Viskoz alt tabakada sadece viskoz
sürtünme önemlidir. Viskoz alt tabaka ile türbülent merkez arasında, hem viskoz sürtünmenin
hem de girdap sürtünmesinin olduğu bir geçiş tabakası bulunur. Bu geçiş bölgesi tampon bölge
olarak isimlendirilir ve nispeten ince bir tabakadır. Kalan akış alanı, türbülent merkez olarak
isimlendirilen akış tarafından kaplanır. Türbülent merkez içinde viskoz kesme, türbülent
viskoziteden kaynaklanan kesmeye nazaran ihmal edilir. Şekil 3’te Reynolds deneyi ve akış
rejimlerinde boya izi şematik olarak gösterilmektedir.
Şekil 3. Reynolds deneyi ve akış rejimleri.
3
2.3. Laminer Akış
Şekil 4’de, içinde Newtonian bir akışkanın bir boyutlu kararlı hal laminer akışta aktığı bir
borunun yatay kesiti gösterilmektedir. Akış tam gelişmiştir; yani akış giriş etkileri tarafından
etkilenmemekte ve x-yönünde akış ekseni boyunca değişmemektedir.
Şekil 4. Borusal akışta kuvvet denkliği.
Silindirik kontrol hacmi, iç çapı r, kalınlığı
r ve uzunluğu
x olan bir kabuktur. Kararlı halde,
momentum korunum eşitliği
|
|
|
|
r yarıçapındaki silindirik yüzeye etki eden kayma kuvveti veya sürükleme kuvveti, kayma
gerilimi ( rx ) ile akış kesitinin ( 2 r x ) çarpımı kadardır. Bununla birlikte bu büyüklük, aynı
zamanda kabuğun silindirik yüzeyine momentum akış hızı olarak ta düşünülebilir. Bundan
dolayı, net momentum akışı:
|
x’teki akışkan hızı x , x + x teki akışkan hızı
|
x
eşit olduğundan,x ve x+ x halkasal
yüzeylerden net taşınım momentum akısı sıfırdır, çünkü akış tam gelişmiş olup terimler x’ten
bağımsızdır.
Eşitlik (3) ve (4) birbirine eşitlenir ve yeniden düzenlenirse aşağıdaki ifade elde edilir:
( r rx ) | r r ( r rx ) | r
r
r ( p |x p |x r )
Tam gelişmiş akışta, basınç gradienti ( p/ x) sabittir ve ( p/L)’ye eşit olur; burada
uzunluğundaki boru için basınç düşüşüdür.
(5)
x
p, L
r sıfıra yaklaştığında, aşağıdaki eşitlik elde edilir,
4
d ( r rx ) |
dr
p
L
r
(6)
Değişkenlerine ayrılır ve integre edilirse aşağıdaki ifadeyi verir:
C1
p r
r
L 2
rx
(7)
r = 0’da momentum akısı sonsuz olmadığından, integrasyon sabiti C1 = 0 olmalıdır. Bundan
dolayı;
rx
p
2L
p0 pL
r
r
2L
(8)
Bu ifade, momentum akısının, akışkanın aktığı borunun çapı ile doğrusal olarak değiştiğini
gösterir ve maksimum değer r = R’de (duvarda) meydana gelir. Aşağıdaki (9) eşitliği ile verilen
Newton Viskozite Yasası, Eşitlik (7)’de yerine yazılırsa, hız için aşağıdaki diferansiyel eşitlik
(10) elde edilir:
du
rx
du
x
dr
(9)
x
dr
p0 pL
2L
r
(10)
Duvarda, r = R (duvar), ux = 0 sınır koşulu kullanılarak integrasyon yapılırsa, hız dağılımı için
aşağıdaki bağıntı (11) elde edilir:
p0 pL
ux
4L
r
R 1
R
2
2
(11)
Bu sonuç, laminer bir akış için yarıçapa göre hız dağılımının, boru ekseninde maksimum olan
bir parabol şeklinde olduğunu gösterir.
U
ort
1
A
u
x
dA
A
2 R
1
R
2
u
x
rdrd
0 0
R
1
R
2
u
x
2 rdr
(12)
0
(11) ve (12) eşitlikleri birleştirilir ve integre edilirse aşağıdaki ortalama hız eşitliği (13) elde
edilir:
U
ort
( p0 pL )
8L
R
2
5
( p0 pL )
32 L
D
2
(13)
Burada çap D = 2R’dir. Dolayısıyla, Hagen–Poiseuille eşitliği olan Eşitlik (13), yatay bir
borudaki laminer akış için basınç ve ortalama hız arasındaki bağıntıyı verir. Bir boruda akan
akışkanın maksimum hızı r = 0 (boru merkezinde) meydana gelir ve Eşitlik (11)’den
hesaplanabilir,
U
m ax
p0 pL
4L
R
2
(14)
(13) ve (14) eşitlikleri birleştirilir ve düzenlenirse ortalama hız ile maksimum hız arasında
aşağıdaki eşitlik elde edilir.
U
ort
U
m ax
(15)
2
3. Deney Düzeneği
Deney düzeneği Şekil 5’de kabaca gösterilmektedir. Deney düzeneği bir su tankı, pompa, akış
kontrol vanası, şeffaf bir boru (cam veya akrilik) ve bir de boya haznesinden ibarettir.
a
b
Şekil 5. Deney düzeneği; A: Pompa, B: Vana, C: Renkli sıvı haznesi, D: Cam boru
Deney esnasında akış bölgeleri, boruya merkezden enjekte edilen renkli sıvının akış deseni
görsel olarak incelenerek belirlenecektir. Üç farklı akış bölgesinin karakteristik özellikleri, akış
desenindeki sürekli değişim gözlenerek ve ortalama hızları ölçülerek laminerden geçiş bölgesine,
geçiş bölgesinden türbülent akışa dönüşümlerin hangi Reynolds sayılarında meydana geldiği
deneysel olarak belirlenecektir.
6
Deney düzeneğini çalıştırmak ve deneyleri yapmak için;
Pompa çalıştırılarak suyun tüm akış borusunda hiçbir hava kabarcığı kalmaksızın akışı
sağlanmalıdır.
Renkli sıvının musluğu yeterli ölçüde açılarak akış borusuna enjektörden renkli sıvı girişi
sağlanmalıdır.
Akış hızı, vana kullanılarak akışı minimuma getirerek renkli sıvının, dalgalanma ve kopma
olmadan ince bir iplikçik halinde akışı sağlandığında gözlenen durum laminer akış şartlarıdır.
Laminer akış konumunda, boyanın boru merkezine verildiğini kabul ederek, iki nokta
arasında renkli sıvı hattında oluşturulacak bir iz takip edilerek belirlenen iki nokta arasında bu
izin geçiş süresi belirlenir. Bu verilerden akışkanın merkezdeki maksimum hızı hesaplanır.
Akışın ortalama çizgisel hızını belirlemek amacıyla, hızı değiştirmeden, su çıkışına
yerleştirilecek ölçekli bir kapla mevcut akışın hacimsel debisi ölçülür. Bunun için belirli bir
hacmi ne kadar sürede doldurduğu belirlenir ve bu verilerden ortalama çizgisel akış hızı
hesaplanır.
Bu değerlerden laminer akışta ortalama ve maksimum hızların oranı ve Reynolds sayısı
hesaplanır.
Daha sonra vana çok yavaş ve kontrollü bir şekilde açılarak, akışın laminerden geçiş
bölgesine dönüştüğü hızı yakalanmaya çalışılır (ince boya izinin dalgalanmaya başladığı hız).
Bu hızda yine ölçekli bir kap ile ortalama hız belirlenir ve gözlemlenen akışın Reynolds sayısı
hesaplanarak 2100’le karşılaştırılır.
Yine vana çok yavaş ve kontrollü bir şekilde açılarak, akışın geçiş bölgesinden türbülente
dönüştüğü hız yakalanmaya çalışılır (dalgalanmakta olan boya izinin kırılmalara maruz kalıp,
boru kesit alanına yayılmaya başladığı hız). Bu hız da, yine ölçekli bir kap ile ortalama hız
belirlenir ve gözlemlenen akışın Reynolds sayısı hesaplanarak 4000’le karşılaştırılır.
4. Deney Sonuçlarının Değerlendirilmesi
Her denemede hacimsel debi ölçümünde elde edilen veriler kullanılarak cm3/s olarak
hacimsel debiler hesaplanacaktır. Süreklilik eşitliği kullanılarak boru için elde edilen
hacimsel debi verilerinden boruda akan akışkanın ortalama lineer hızı belirlenecektir.
7
Elde edilen Uort. hızları kullanılarak bu veri çiftlerinin elde edildiği adımlardaki Re sayıları,
yani akış bölgeleri belirlenecek ve gözlemlerinizle farklı çıkıp çıkmamaları irdelenecek ve
yorumlanacaktır.
Laminer akışta renkli sıvının a ve b noktaları arasındaki mesafeyi alma süreleri borudaki
akışkanın maksimum hızını belirlemek için kullanılacaktır. Umax = x/t (cm/s) bağıntısı
kullanılarak farklı her deneme için Umax. değerleri hesaplanacaktır.
Laminer bölge için elde edilen Umax. ve Uort hızları kullanılarak (Uort./Umax) oranları
hesaplanarak,
laminer bölge için Uort./Umax = 0.5 literatür değeri ile kıyaslanacak ve
sonuçların bu değerden farklı çıkması halinde bunun sebepleri izah edilerek yorum şeklinde
yazılacaktır.
Akış desenindeki sürekli değişim gözlenerek ve ortalama hızları ölçülerek deneylerden tespit
edilen laminer akıştan geçiş bölgesine, geçiş bölgesinden türbülent akışa dönüşüm
gözlemlerinden elde edilen Reynolds sayısı değerlerinin teorik değerlerle karşılaştırılarak
sonuçları yorumlanır.
4. Semboller
D: boru çapı
F: kuvvet
Fs: sürtünme kuvveti
Fg: yerçekimi kuvveti
P: basınç(kg.m2)
Uort : ortalama lineer hız
Umax: maksimum hız
ux: yerel
r: radyal yöndeki mesafe
R: boru cidarından olan radyal yöndeki uzaklık
x: eksenel yöndeki mesafe
rx: kesme gerilimi
w: boru cidarındaki kesme gerilimi
: akışkanın yoğunluğu
: akışkanın viskozitesi, (kg/m.s)
: akışkanın kinematik viskozitesi, (m/s)
8
5. Kaynaklar
1- Taşınma Süreçleri ve Ayırma Süreci İlkeleri, Christie John Geankoplis, Çev. SinanYapıcı,
4. Baskıdan Çeviri, İzmir Güven Kitabevi, 2011.
2- Akışkanlar Mekaniği: Temelleri ve Uygulamaları, Yunus A. Cengel, John M. Cimbala, Çev.
Editör: Tahsin Engin, 3. Baskıdan Çeviri, İzmir Güven Kitabevi, 2013.
6. Deneye Hazırlık Soruları
1.
Akışkan nedir, akışkanlar mekaniğinde akışkanlar kaç guruba ayrılır, açıklayınız?
2.
Laminer akış ve türbülent akış nedir, bu akış türleri neye göre ayırt edilir?
3.
Çizgisel hız, hacimsel hız ve kütlesel hız kavramlarını açıklayarak birbirleri ile olan
ilişkilerini matematiksel olarak ifade ediniz ve süreklilik eşitliğini türetiniz.
4.
Reynolds sayısının fiziksel anlamını yazınız.
5.
Kayma gerilimi, viskozite ve kaymazlık şartı nedir kısaca açıklayınız.
6.
Hız profili, sınır tabaka, borusal sistemlerde, gelişmekte olan akış ve tam gelişmiş akış ne
demektir açıklayınız?
7.
Ortalama hız, lokal hız, edi (girdap, burgaç, anafor) ne demektir açıklayınız?
8.
Dairesel kesitli bir sistemde maksimum akış hangi konumda gerçekleşir, tam gelişmiş,
dairesel kesitli laminer akışta Uort/Umax= 0.5 olduğunu gösteriniz?
9.
Akış içeren herhangi bir sistemde, katı yüzey üzerindeki akış hızının değeri ne olur, fiziksel
olarak yorumlayınız?
10. Hagen–Poiseuille eşitliği nedir, nasıl türetilebilir?
9