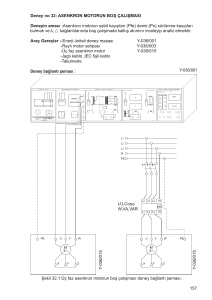
BÖLÜM 4
DINAMIK GERILIM KARARLILIĞI
Sürekli hal gerilim kararlılığı analizleri, çeşitli işletme koşulları altında,
iletilen güç ile hat sonu geriliminin değişimini ve kritik değerlerin (Prcrit, Vrcrit) bu
işletme koşullarıyla etkileşimlerini belirlemek ve P-V eğrileri yardımıyla bu
değişimleri açıkça izlemek açısından oldukça yararlı olmasına karşılık, yüklerin
dinamiğine bağlı olarak hızlı değişen olayların açıklanmasında yetersiz kalmaktadır.
Zira statik analizlerde P-V eğrilerini karakterize eden olayların, dakikalardan saatler
mertebesine uzanan geniş periyotlar içinde oluştuğu öngörülmektedir. Oysaki,
paralel çalışan iletim hatlarının birinin devre dışı olması ve hat sonundaki yüklerin,
ağırlıklı olarak sabit aktif güç çekme eğilimli asenkron motor yüklerinden oluşması
durumunda, bu tür yüklerin hızlı transiyent karakteristikleri nedeniyle, yerel olarak
ani gerilim çökmeleri görülebilecektir. Buna paralel olarak, koruma düzenlerinin de
hızlı değişen böyle olaylara cevap verebilecek nitelikte olması gerekecektir.
Bunlara dayanarak, dinamik gerilim kararlılığı incelenirken; dinamik yük
modeli, temel denklemler ve simülasyonun işleyişi ele alınacak, dinamik gerilim
kararlılığımı etkileyen faktörler ve korunma yöntemleri gözden geçirilecektir.
Özellikle iletim hatları açısından, dinamik gerilim kararlılığı etkileşimleri ayrıca
incelenecektir.
4.1.
Dinamik Yük Modelleri
Klasik yük akışı analizlerinde, her yük düğümündeki aktif ve reaktif güçlerin
sabit olduğu kabul edilmektedir [44]. Oysa ki gerçek sistemde bu yükler zamanla
değişmektedirler. Bu değişim, normal yük artımı veya azalması şeklinde olabileceği
gibi, şekil (4.1) ' den görüleceği üzere, bir baradaki gerilim artışını aynı şekilde
izleyen ve daha sonra yaklaşık olarak başlangıç değerine düşen bir güç değişimi,
özellikle dinamik simülasyon için tipik bir örnektir. 2. bölümde elektriksel yükler
incelenirken, yüklerin karakteristikleri bakımından; sabit empedans, sabit akım ve
sabit güç yükleri olarak üç ana gruba ayrıldıkları ve pratikte bir yükün, zaman içinde,
bir gruptan başka bir gruba geçebildiği görülmüştü.
42
V
P
t
Şekil 4.1. Sabit güç yükünün adım cevabı
Şekil 4.1. ' de, ilk anda gerilim azalmasıyla orantılı azalan yük, tipik bir sabit
bir empedans yüküdür. Bunun nedeni, motorun kütle ataleti veya kontrolör
cevabının gecikmesi olabilir. Daha sonra ise, mekanik motor yükünün öz-kontrollu
sabit güç karakteristiği veya kontolörün sabit güç karakteristiği nedeniyle yük, sabit
gücüne dönmektedir [21].
Sabit empedans yükleri, gerilim kararlılığı bakımından paralel hatlardan
birinin açması gibi büyük bir bozucu etki altında dahi bir gerilim kararsızlığına yol
açmazlar. Zira 2. bölümde açıklandığı gibi, gerilim değerindeki bir birim azalma güç
değerinde yaklaşık iki kat azalmaya neden olmaktadır. Bunun sonucunda, kritik güç
değeri azaldığı halde, yükün çektiği güç bu değerin altında kaldığı için, sabit
empedans yükleri kararsızlığa yol açmadıkları gibi, sabit güç yükleriyle karma
yükler oluşturmaları durumunda, gerilim kararlılığını olumlu yönde etkilemektedir.
Dinamik yük elemanları ise iki grupta toplanabilir. Motorların hızlı geçici
karakteristikli olmalarına karşılık, kontrollu omik yükler veya yük altında kademe
değiştiriciler daha yavaş geçici karakteristiklidirler [45]. Başlangıç olarak, kontrollu
omik yükün dinamiğini tanıtmak statik ve dinamik yaklaşımlar arasında bir geçiş
olması açısından yararlı gözükmektedir. Buna göre, örnek iletim hattının sonuna,
kontrollu bir omik yük bağlandığı varsayılsın. Bu yükün dinamiği birinci
mertebeden bir gecikme modeliyle gösterilebilir [46], [47].
dG
TL
Po G. Vr2
(4.1)
dt
Burada;
TL
Vr
G
Po
: yükün zaman sabiti,
: yük Gerilimi,
: sabit güce ayarlanabilen yükün kondüktansı,
: sabit gücü ifade etmektedir.
43
Şekil 4.2. Kontrollu omik yükün dinamiğinin PV eğrisi üzerinde yorumlanması
Şekil 4.2. üzerinde aynı Po gücü için, gerilimin normal ve düşük olduğu
noktalar göz önüne alınırsa,
Po = Ga.Va2 = Gb.Vb2 ifadesinde Va
Vb buna karşılık Ga
Gb 'dir yani
düşük gerilim bölgesindeki yük kondüktansı üst gerilim bölgesindekinden daha
küçük değerdedir (değere ayarlanmıştır). Bu iki nokta esas alınarak, eğri üzerinde
belli bölgeler tanımlanabilir ve bu bölgeler için dinamik olaylar, (4.1) denklemine
şöyle yorumlanabilir :
Başlangıç noktası, (1) - (2) arasındaki bölgede ise G
Ga olacağından,
dG
dG
0 (pozitif) 'dir ve dolayısıyla işletme noktası,
0 olan (a) noktasına oturur.
dt
dt
Başlangıç noktası, (2) - (3) - (4) arasındaki bölgede herhangi bir yerde ise
dG
0 (negatif) 'tir ve dolayısıyla işletme noktası, (a)
Ga G Gb olacağından,
dt
noktasına kayar.
Başlangıç noktası, (4) - (5) arasındaki bölgede ise Gb G olacağından,
dG
0 (pozitif) 'dir ve dolayısıyla işletme noktası, (b) noktasından gittikçe
dt
uzaklaşır.
Bu çalışmada, basitlikleri ve fiziksel özelliklerinin kolay anlaşılır olması
nedeni ile, dinamik yük elemanı olarak asenkron motorlar ele alınacaktır [48], [49],
[50]. Gerek işletme noktalarının açık olarak görülebilmesi, gerek çalışma
bölgeleriyle ilgili yorumlamalar bu tür bir örnekle daha net olarak ortaya
konulacaktır.
44
4.2.
Temel Denklemler
Dinamik gerilim kararlılığını incelemek amacıyla, bir güç sistemini
tanımlayan temel denklemleri sıralamadan önce, asenkron motoru kısaca ele almak
yararlı olacaktır [51].
Şekil 4.3 Asenkron motorun basitleştirilmiş eşdeğer devresi.
V1: Stator faz-nötr gerilimi
r1 : Stator bir faz sargısının direnci x1: Stator bir faz sargısının kaçak reaktansı
r2': Rotor bir faz sargısının direncinin x2': rotor kaçak reaktansının
statora
indirgenmiş
statora indirgenmiş değeri
değeri
no: [d/d] senkron devir sayısı
2. . n o
no n
s
: senkron açısal hız
: kayma
o
no
60
Motorun şebekeden çektiği aktif ve reaktif güçler, şekil 4.3 ' teki eşdeğer
devreye göre belirlenerek temel denklemlere katılacaktır. Bunun yanında asenkron
motorun gerilim kararlılığı açısından son derece önemli olan iki karakteristiğini de
göz önüne almak gerekir.
45
a)
b)
Şekil 4.4. Asenkron motorun a) farklı kaymalarda P-V eğrileri. ( s4 s3 s2 s1 )
b) (1) : uç gerilimi nominal değerinin yarısında iken , (2) : uç gerilimi
nominal değerinin % 75 ' inde iken, (3) uç gerilimi nominal değerinde
iken, devir sayısı - moment karakteristikleri.
Dinamik simülasyonu gerçekleştirmek için gerekli temel denklemler şu
şekilde sıralanabilir :
46
Yük akışı denklemleri :
N
T1(k) :
N
Pek
Gkj .Vej
Bkj .V fj .Vek
j 1
N
T2(k) :
Gkj .V fj
Bkj .Vej .V fk
0
(4.1)
Gkj .V fj
Bkj .Vej .Vek
0
(4.2)
j 1
N
Qek
Gkj .Vej
Bkj .V fj V fk
j 1
j 1
bu denklemlerde,
Gkj , Bkj
: k. ve j. düğümler arasındaki hattın kondüktas ve suseptansını,
Vek , Vfk
: k. düğüm geriliminin reel ve imajiner bileşenlerini,
Pek , Qek
: k. düğüme verilen aktif ve reaktif güçleri
göstermektedir.
Asenkron motor :
Şekil (4.3) ' e göre;
T3(k) : Pek
T4(k): Qek
r2' / s k
r1
r1
2
'
2
r / sk
r1
r / sk
x
x 2'
x1
'
2
x1
' 2
2
2
x1
x
' 2
2
Vek2
V fk2
0
(4.3)
Vek2
Vek2
0
(4.4)
rt= r1 + r2' / sk , xt = x1 + x2' tanımlarıyla
rtk , xtk : k. asenkron motorun eşdeğer devresinin omik direnci ve reaktansını
sk
: k. motorun kaymasını göstermektedir.
Sürekli halde,motorun elektriksel giriş gücü (Pek), mekanik yükle (Pmk)
dengededir. Bunu şu eşitlikle göstermek mümkündür ;
T5(k) : Pek(1-sk) - Pmk = 0
(4.5)
Asenkron motorun dinamik denklemi, Ek E ' de gösterildiği gibi, hareket
denkleminden türetilebilir. Bu denklem kaymanın fonksiyonu olarak şu şekilde elde
edilmiştir ;
T6(k) :
burada,
dsk
dt
1
Ik .
2
o
Pmk
1 sk
Pek
(4.6)
47
Ik
fo
wo= 2 fo ,
: k. asenkron motorun atalet momentini,
: güç sisteminin frekansını
: açısal hızı,
göstermektedir.
4.3.
Simülasyonun Işleyişi
Dinamik simülasyonun ilk adımı olarak, klasik yük akışı denklemlerinin (T1,
T2) ve yük karakteristik denklemlerinin (T3,T4,T5) nümerik olarak çözüldüğü
Newton-Raphson metodu ile, sürekli hal çözümleri yapılır.
Ikinci adımda, gerilim çökme sürecinin bir bozucu etki ile tetiklendiği kabul
edilerek, bir transiyent çözüm elde edilir. Bu bozucu etki; paralel çalışan hatlardan
birinin devre dışı olması veya motorun mekanik yükünün adım artımı ya da
generatör, senkron kompanzatör veya statik bir yerel VAr kaynağının devre dışı
olması şeklinde göz önüne alınabilir.
Ilk bozucu etki oluştuğunda, kütle ataletinden dolayı motorun kayması sabit
kalır. Dolayısıyla bozucu etki öncesinde ve hemen sonrasında motorun eşdeğer
empedansı (dolayısıyla yük empedansı) değişmemektedir. Bu hipotez altında, yük
akışı hesaplamalarıyla, başlangıç durumuna ilişkin çözüm elde edilir.
Daha önce kabul edildiği gibi, generatörlerin ve iletim hatlarının transiyent
davranışlarının, yüklerinkinden daha önce bastırıldığı varsayılmıştır. Bu hipotez,
genellikle büyük güç sistemlerinde geçerlidir.
Bu hipotez altında, gerilim
çökmesinin transiyent davranışları şu şekilde hesaplanmaktadır :
Asenkron motorların kaymalarının hesaplanması
Asenkron motorların t +
t anındaki kaymaları, güç sisteminin t anındaki
durumu göz önüne alınarak, T6 dinamik denkleminin, 4. mertebe Runge-Kutta
metodu kullanılarak çözümü ile hesaplanır.
48
Güç sisteminin yeni durumunun oluşturulması
Güç sisteminin, her düğümdeki gerilim, aktif güç ve reaktif güçleriyle temsil
edildiği yeni durumu, yük akışı denklemlerinin ve yük karakteristik denklemlerinin
(T1,T2, T3,T4) çözümü ile elde edilir.
Dinamik simülasyonun akış şeması şekil (4.3) ' te gösterilmiştir.
Baþla
Yük akýþý ile baþlangýç koþullarýnýn
hesaplanmasý
Ýlk bozucu etkiden sonraki hesaplamalar,
Bozucu etkiler :
1.Paralel hatlardan birinin devre dýþý olmasý
2.Mekanik yükün adým artýmý
3.Yerel VAr kaynaðýnýn devre dýþý olmasý
t anýnda, asenkron motorlarýn kaymalarýnýn
Runge-Kutta metodu ile hesaplanmasý
t anýnda sistem koþullarýnýn yük akýþý
ile hesaplanmasý
t+ t
Şekil 4.5. Dinamik simülasyona ilişkin akış şeması