ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
Prof. Dr. Mustafa DEMİR
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
1
z Analitik kimyacıların laboratuarlarda elde ettikleri
sonuçların ne oranda doğru olabileceği bazı
yöntemlerle tahmin edilebilir.
z Analizcinin elde ettiği sonuç rakamla ifade
edilmeli, bu sonucun elde edilmesi sırasında
mümkün hata kaynakları ve bu hataların sonuç
üzerindeki etkisi belirtilmelidir. .
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
2
zSağlıklı bir analiz sonucu elde edebilmek
için analiz en az üç kez değişik örneklerle
tekrarlanmalıdır.
zBir veya iki analiz ile elde edilen sonucun
gerçeği ne derecede yansıttığını tahmin
etmek oldukça güç hatta olanaksızdır
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
3
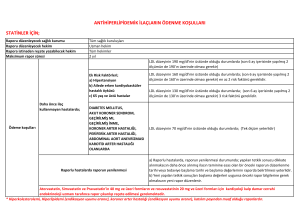
DOĞRULUK VE DUYARLILIK
z Doğruluk (Accuracy); analiz sonucunun gerçek
değere ne kadar yakın olduğunun, duyarlılık
(Precision) ise yapılan ölçümlerin birbirine ne
ölçüde yakın olduğunun ifadesidir.
z Bir analizde ölçümlerin duyarlılığı gerçeğe en
yakın bir şekilde her zaman hesaplanabilir.
Ancak gerçek değer tam olarak bilinmezse
sonucun doğruluğu ancak tahmin edilebilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
4
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
5
Illustrating the difference between “accuracy” and “precision”
Low accuracy, low precision
Low accuracy, high precision
High accuracy, low precision
High accuracy, high precision
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
6
zBir ölçümde, duyarlılığın çok iyi olması
onun doğruluğunun da çok iyi olduğunu
göstermez, ancak gerçeğe yakınlığı
konusunda bir fikir verebilir.
zÖrneğin, içinde tam %20 demir bulunan bir
karışımın analizi sonunda bulunan yüzde
demir miktarı sonucun doğruluk derecesi
hakkında bir fikir verir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
7
z Öte yandan içindeki gerçek demir miktarı
bilinmeyen bir filizin analizi sonunda bulunan
yüzde demir, o değerin doğruluğu konusunda bir
şey söylemez.
z Bu sonucun elde edilmesi sırasındaki ölçümlerin
birbirine yakınlığı yani ölçümün duyarlılığı ise
bulunan sonucun doğruluğu konusunda bir fikir
verir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
8
zDoğruluk, ölçümlerin aritmetik
ortalamasının gerçek değere yakınlığı
olarak tanımlanır ve hata olarak ifade
edilir.
zDuyarlılık ise ölçümlerin birbirine yakınlığı
olarak tanımlanır ve sapma olarak ifade
edilir.
zDuyarlılık, aynı değeri yeniden elde etme
becerisi olarak da tanımlanır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
9
zİyi bir duyarlılık çoğunlukla iyi bir doğruluk
derecesinin göstergesidir.Ancak bu her
zaman geçerli değildir.
zÇok iyi bir duyarlılığı olduğu halde zayıf
doğruluk dereceli ölçümler de olabilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
10
SAPMA
ölçümlerin
duyarlılığının
bir
ifadesidir ve çeşitli şekillerde tanımlanır.
Bir kimyasal analizde yapılan ölçümlerin
ölçüm sayısına bölünmesi sonunda bulunan
sayıya ortalama değer denir ve
olarak
gösterilir.
Sapma
N
x =
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
∑ xi
i=1
N
11
Mean ( x ) : average of the numerical data
mean, x =
M.DEMİR(ADU)
∑x
i
n
i
1
= ( x 1 + x 2 + x 3 + ... + xn )
n
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
12
Ortalama değer ile her bir ölçüm
arasındaki farka ise mutlak sapma denir.
Örneğin ikinci ölçümün mutlak sapması
x2 nin mutlak sapması =
olarak yazılabilir.
Genel olarak
M.DEMİR(ADU)
d i = xi − x
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
13
zÖlçümlerde mutlak sapma pek
kullanılmaz, bunun yerine daha çok yüzde
ve binde göreli (relatif) sapma kullanılır.
Göreli sapma, mutlak sapmanın ortalama
değere bölümü ile bulunur. Bunun 100
veya 1000 katma yüzde veya binde göreli
sapma denir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
14
Her bir ölçümün yüzde göreli sapması =
Her bir ölçümün binde göreli sapması
şeklinde gösterilebilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
15
Buna göre ikinci ölçümün yüzde
göreli sapması =
olarak yazılır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
16
zAnalitik değerlendirmelerde her bir
ölçümden çok ortalama değerlerle
ilgilenilir. Bunun için ortalama sapma,
standart sapma ve ölçüm aralığının
hesaplanması gerekir
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
17
Ortalama sapma
Her bir ölçümün mutlak sapmalarını toplamının
ölçüm sayısına bölümüne denir.
Ortalama Sapma(OS)
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
18
Örnek 1.
zAşağıdaki ölçümlerin ortalama sapmasını
hesaplayınız.
z12.0, 10.6, 1.2, 10.8, 11.4
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
19
zÇözüm için önce verilerin ortalamasının
bulunması gerekir.
zEğer hesaplama yapılırsa 11.2 olarak
bulunur.
zBu değer ile her bir ölçüm arasındaki fark
alınır ve işlem yapılırsa ortalama sapma
0.4 olarak bulunur.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
20
Xi
0.8
0.6
0.0
0.4
0.2
12.0
10.6
11.2
10.8
11.4
z =(0,8+0,6+0,0+0,4+0,
2)/5
z =(2,0/5)
z =0,4
=11.2
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
21
Göreli (Relatif) Ortalama Sapma
Ortalama sapmanın
bölünmesiyle bulunur.
ortalama
değere
Relatif Ortalama Sapma(ROS) =
Relatif ortalama sapmanın 100 veya 1000
katına yüzde veya binde relatif ortalama
sapma denir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
22
Örnek 2:
zAşağıdaki ölçümlerin relatif ortalama
sapmasını hesaplayınız.
z60.44, 60.30, 60.72, 60.54
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
23
Xi
60.44
60.30
60.72
60.54
M.DEMİR(ADU)
0.06
0.20
0.22
0.04
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
24
Standart Sapma, S
zDuyarlılığın ölçümü için daha geçerli
bir birimdir.
zHer bir ölçümün mutlak sapmalarının
kareleri toplamının ölçüm sayısının bir
eksiğine bölümünün kareköküne
eşittir ve S ile gösterilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
25
S=
M.DEMİR(ADU)
2
∑ ( x i − X)
n −1
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
26
Örnek 3:
zAşağıdaki ölçümlerin standart
sapmasını hesaplayınız.
z10.5, 9.9, 10.4, 9.5, 9.6, 11.5, 9.0,
10.0, 10.5, 9.0, 10.1
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
27
Xi
10.5
9.9
9.5
10.4
9.6
11.5
9.0
10.0
10.5
9.0
10.1
X = 10.0
M.DEMİR(ADU)
( xi − X ) 2
Xi − X
0.25
0.01
0.25
0.16
0.16
2.25
1.00
0.00
0.25
1.00
0.01
0.5
0.1
0.5
0.4
0.4
1.5
1.0
0.0
0.5
1.0
0.1
n
∑
i =1
xi − X
2
5.34
S=
= 0.73
10.0
= 5.34
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
28
Relatif (göreli) standart sapma, Srel
zStandart sapmanın ortalama
değerine bölümüne denir. Yüzde
veya binde relatif standart sapma
olarak ifade edilir, Srel olarak
gösterilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
29
Örnek 4
zYukarıdaki örneğin yüzde relatif
standart sapmasını hesaplayınız
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
30
S
0.73
Yüzde Relatif standart sapma(Srel ) = x100 =
x100 = 7.3
10
X
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
31
Ölçüm aralığı
zBir analizde en büyük ve en küçük değerli
ölçümlerin farkına denir ve ω ile gösterilir.
zBir analizdeki ölçümün ortalama değerlere
göre sıralandığı ve en son terimin n olduğu
düşünülürse;
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
32
ω = X n − X1
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
33
zolarak yazılabilir.
zEn kolay hesaplanan bir değerdir.
zBir analizdeki ölçüm sayısı 2 ile 4 arasında
ise ölçümlerin duyarlılığı hakkında fikir
edinmek için standart sapma yerine ölçüm
aralığına bakmak daha doğru fikir verir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
34
zÖlçüm sayısı 10’dan fazla ise, ölçüm
aralığı hemen hemen bir anlam ifade
etmez, standart sapma daha doğru fikir
verir.
zÖlçüm sayısı 4 ile 10 arasında olduğunda
ise, ölçüm sayısı hangi sınıra yakın ise o
birimi daha doğru fikir verir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
35
Örnek 5
zYukarıdaki örnek 2 nin ölçüm aralığını
hesaplayınız.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
36
zBu ölçümler büyüklük sırasına göre
dizilirse 60.30, 60.44, 60.54, 60.72 dizisi
elde edilir. Buna göre ölçüm aralığı
z
ω = 60.72 – 60.30 = 0.42 bulunur.
zBu örneğin standart sapması hesaplanırsa
0.1766 olduğu görülür.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
37
zBir analizin sonucu yazılırken yapılan
her ölçümün ayrı ayrı hesaplanması
gerekmez.
zBunun yerine bunların ortalamasının
yazılması yeterlidir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
38
zAncak bu ortalamanın bir anlam ifade
edebilmesi için ölçüm aralığının,
standart sapmasının ve kaç ölçümün
yapıldığının belirtilmesi gerekir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
39
Hata
zBir ölçümün sonucunun gerçek
değere yakınlığının bir ifadesidir.
zSapmada olduğu gibi hatada da
mutlak hata, ortalama hata ve göreli
ortalama hata olarak ifade edilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
40
zOrtalama hata: bir dizi ölçümün
ortalaması ile gerçek değer arasındaki
farka denir.
zRelatif (göreli) ortalama hata ise,
ortalama hatanın gerçek değere bölümü
sonunda bulunan değerdir.
zBu da sapmada olduğu gibi yüzde veya
binde göreli hata olarak ifade edilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
41
zAnalitik kimyada ölçümlerin anlamlı
olabilmesi için ne tür hataların
yapılabileceğinin, bunların ne kadarının
giderilebileceğinin ve bu hataların sonucu
ne ölçüde etkileyebileceğinin bilinmesi
gerekir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
42
Hata kaynakları
zBir ölçmede karşılaşılabilen hatalar
belirli ve belirsiz hatalar olmak üzere
iki grupta toplanabilir.
zBelirli hatalar fark edilebilirler ve daha
dikkatli çalışma ile giderilebilirler.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
43
zBelirsiz hatalar ise belirsizliğin neden
olduğu düzensiz hatalardır.
zBöyle bir hatanın yapıldığı fark
edilemez ve ne kadar dikkatli
çalışılırsa çalışılsın tamamen
giderilemez.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
44
Belirli hatalar
z Birçok kaynaktan gelebilir. Nedenlerin ortadan
kaldırılmasıyla giderilebilir.
z Bu tür hatalara sabit hatalar da denir.
z Her analizdeki bu tür hatanın nedeni farklı
olmamakla birlikte her hatanın büyüklüğü bütün
analizlerde aynıdır.
z Bu tür hatalar dört grupta incelenebilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
45
1.Kullanılan aletten gelen hatalar
zAnalitik kimyada kullanılan her aracın belli
doğruluk sınırı vardır.
zÖrneğin 50 ml’ lik bir büret ne kadar iyi
ayarlanmış olursa olsun 0.05 ml’lik bir hata
ihmali taşır.
zAynı şekilde lâboratuvarlarda kullanılan
teraziler, gramlar, cam araç ve gereçler
belli bir hata olasılığı taşır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
46
zÖlçümlerde kullanılan her aracın hata
sınırının bilinmesi gerekir.
zYanlış ayarlanmış bir terazi, yanlış yapılan
bir tartım veya yanlış ayarlanmış bir
büretin neden olduğu hatalar basit
denemelerle fark edilebilirler veya
kolaylıkla giderilebilirler
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
47
2.Ayıraçtan gelen hatalar
z Analizlerde kullanılan bütün kimyasal
ayıraçlar çok az da olsa safsızlık içerirler.
z Analitik ölçümlerde örnek içindeki hangi
maddelerin analizi olumsuz yönde
etkileyebileceğinin bilinmesi ve eğer böyle
bir madde varsa bunun giderilmesi gerekir.
z Ayrıca kullanılan ayıraç içindeki
safsızlıkların da iyi bilinmesi gerekir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
48
z Duyarlı analizler için yalnız Analitik Ayıraç
denilen ve ambalaj kabı üzerine o ayıraçtaki
safsızlıkları belirtilen ayıraçların kullanılması
gerekir.
z Bunların üzerinde safsızlıkların yüzdeleri
verildiğinden bu ayıraçtan kullanılan miktar
dikkate alınarak buradan gelecek hatanın
en fazla ne kadar olabileceği hesaplanabilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
49
3.Analiz yöntemine bağlı olan hatalar
zHata kaynaklarının önemlilerinden biri
de her yöntemin kendine özgü hata
olasılıklarıdır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
50
z Gravimetrik bir analizde çökeleğin az da olsa
çözünmesi
z Veya ortamdaki başka maddelerin de çökelti
verebilmesi,
z volumetrik bir analizde ortamda bulunan başka
maddelerin de tepkime verebilmesi
z veya uygun bir indikatörün bulunamaması, bu
tür hataların nedenleridir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
51
zÖrneğin; bir filizdeki demir miktarının
gravimetrik yöntemle tayininde, demir
hidroksitin çöktürülmesi sırasında
ortamda, aynı koşullarda çökelti veren bir
madde varsa o da çöker.
zKurutup yakma işlemlerinden sonra o da
tartılacağından bulunacak demir o oranda
fazla olur.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
52
zÖte yandan çöktürülen demir
hidroksitin bir kısmı çözünürlük
çarpımına bağlı olarak bir miktar
çözünebilir.
zBu da sonucun gerçek değerinden
daha az bulunmasına neden olur.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
53
z Aynı demir gravimetrik yöntemle değil de
volumetrik yöntemle analiz edilirse, gravimetrik
yöntemle birlikte çökelti veren safsızlıklar burada
belki hiçbir sorun yaratmayabilir.
z Fakat bu kez başka safsızlıklar sonucu
etkileyebilir. Örneğin; ortamda herhangi bir
indirgenin bulunması, sonucun yine fazla
bulunmasına neden olabilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
54
zAynı şekilde gravimetrik bir analizde iyi
yıkanmamış bir çökeltide kalan
safsızlıkların neden olduğu hatalar veya
volumetrik analizde yanlış seçilen bir
indikatörün neden olduğu hatalar
yöntemlerin kendine özgü hatalarıdır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
55
4.Analizcinin neden olduğu hatalar
zHatalar içinde belki de en çok
rastlanan ve bizzat analizci tarafından
yapılan hatalardır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
56
z Örneğin;
{bir bürette değerin yanlış okunması,
{çözeltiye yabancı bir iyonun karıştırılması,
{ayıracın biraz fazlaca eklenmesi,
{ortamın pH’ının tam olarak kontrol
edilmemesi,
{çökelti veya çözeltinin bir yerden başka bir
yere aktarılması sırasında dökülmesi,
{baget veya benzeri bir yerde artık kalması
gibi birçok nedenlerle yapılan hatalar bizzat
analizcinin neden olduğu hatalardır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
57
Bu hataların en aza indirilmesi
büyük ölçüde, bu alanda el becerisinin
kazanılmasına ve daha dikkatli çalışmaya
bağlıdır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
58
Belirli hataların giderilmesi
z Analitik ölçümlerde hataların giderilebilmesinin
en iyi yolu, hataların nereden geldiğinin
araştırılması ve bu hatayı gidererek yeni bir
ölçümün yapılmasıdır.
z Ancak bu, gerek örneğin azlığı ve gerekse uzun
zaman alması nedeniyle çoğu kez kolay
olmayabilir.
z Bu durumda yapılacak iş hataların denetlenebilir
şartlarda yapıldığını varsaymak ve buna göre
ölçümlerde bazı düzeltmeler yapmaktır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
59
1.Ayar düzeltmesi
zAletlerin neden olduğu hatalar eğer
gözlenebiliyorsa basit matematik işlemlerle
giderilebilirler.
zÖrneğin; 50 ml’lik bir büretin 50.2 ml’lik
hacmi olduğu biliniyorsa 0.20 ml’lik bir
düzeltme ve her ölçüm sonunda yapılarak
bunun neden olduğu hata giderilebilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
60
z Bazı analitik işlemlerde ise başka tür düzeltmeler
gerekebilir.
z Örneğin; gravimetrik bir tayinde çökeltinin iyice
yıkanması gerekiyor, fakat çözelti, yıkama
çözeltisinde bir miktar çözünüyorsa, çökeltinin
çözünürlük çarpımı ve yıkama çözeltisinin
hacminden yararlanılarak ne kadar çözeltinin
çözündüğü hesaplanıp, bu değerin işlem
sonunda bulunacak değere eklenmesiyle gerekli
düzeltme yapılabilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
61
2.Kör deneme ile düzeltme
z Örnekten bağımsız olarak yapılan hatalar, kör
denemelerle giderilebilir.
z Burada yapılacak işlem, bütün işlemleri hiç
analiz örneği kullanmadan yapmaktır.
z Bu şekilde bulunacak değerin örnek ile birlikte
bulunacak değerden çıkarılmasıyla bir düzeltme
yapılabilir.
z Örneğin; bir asit tayininde önce saf suyun
asitliğinin ölçülmesi ve daha sonra asit
miktarının ölçülmesiyle suyun asitliğinin neden
olduğu hata giderilebilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
62
3. Örnek miktarını değiştirerek yapılan
düzeltme
z Analizi bozan maddelerin neden olduğu hatalar örnek
miktarının değiştirilmesiyle gözlenebilir ve düzeltilebilir.
z Örneğin; örnek miktarı iki katına çıkarıldığında, safsızlık
maddeleri de iki katına çıkacağından hata da iki kat
olması gerekir.
z Böylece bu hatanın safsızlıklardan geldiği anlaşılır ve
gerekli düzeltme yapılabilir.
z Şüphesiz bu tür düzeltme için analizi yapılan maddenin
gerçek değerinin ve analizi bozan maddenin bütün örnek
içinde aynı oranda bulunması gerekir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
63
4.Farklı yöntem kullanarak yapılan
düzeltme
z Birçok analizde olduğu gibi örnekteki maddenin
gerçek miktarının bilinmediği durumlarda farklı
bir yöntemle de analizin yapılması yararlı sonuç
verir.
z Farklı yöntemlerle farklı sonuçların bulunması,
ortamda analizi bozan safsızlıkların
bulunabileceğinin gösterir.
z Bu durumda hatanın nedeninin araştırılması
gerekir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
64
BELİRSİZ HATALAR
z Analitik kimya lâboratuvarlarında yapılan
her ölçümün belli bir belirsizliği vardır.
z Örneğin; her bürette 0.1 ml duyarlılığında
okuma rahatlıkla yapılabilir.
z Ancak 0.01 ml duyarlığında bir okumayı
yapmak ise oldukça güçtür.
z Bu tür hatalara kaçınılmaz veya
değişken hatalar denir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
65
zÖrneğin; yukarıdaki okumayı 0.01 ml
duyarlılığında on ayrı öğrenci yapsa her
birinin bulacağı değer farklı olabilir.
zBu tür hatalar bir dereceye kadar
azaltılabilse de tamamen giderilemez.
zOrtalama değer etrafında düzensiz bir
dağılım gösterir.
zBu tür hatalar için en iyi fikri normal
dağılım eğrisi verir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
66
NORMAL DAĞILIM EĞRİSİ
z Bir analizde ölçüm sayısı arttıkça yapılan
hatanın yalnız belirsiz hatalardan geldiği
kabul edilir.
z Analiz için sonsuz sayıda ölçüm yapıldığı
kabul edilirse buradaki ölçümler; artık
örneğin, birer ölçümü olarak değil ölçümler
kümesi olarak değerlendirilir.
z Bu kümenin aritmetik ortalaması artık X ile
değil µ ile gösterilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
67
z Böyle bir ölçümdeki hata dağılımı normal
dağılım eğrisi denilen eğrilerle gösterilir.
z Aşağıda böyle bir dağılım eğrisi verilmiştir.
z Bu eğride y ekseni belli bir hatanın
tekrarlanma olasılığını yani, xi - µ yü verir.
z X ekseni üzerindeki σ ise kümenin
standart sapmasıdır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
68
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
69
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
70
zNormal dağılım eğrisi başlıca üç
noktayı belirler:
z1. Eğri simetrik olduğundan bir ölçümde
pozitif hatalar kadar negatif hatalarda
vardır. Bu nedenle gerçeğe en yakın
değer aritmetik ortalamadır.
z2. Az hata yapılmış olma ihtimali
fazladır. Toplam ölçümün %68’inin
hatası ±σ kadardır.
z3. Büyük hata yapılmış olma ihtimali
azdır. Toplam ölçümün ancak %1
kadarının hatası ±3σ’dır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
71
zNormal dağılım eğrisi az örnekli
ölçümlerde sonucun hata ihtimalini
tahmin etmekte yardımcı olur.
zÖrneğin; aritmetik ortalaması 10,
standart sapması 0.65 olan bir ölçümde
gerçek değerin %68 ihtimalle 10 ± 0.65
aralığında %95 ihtimalle ise 10 ± 1.30
aralığında olduğunu gösterir.
zBöylece az sayıdaki ölçümler ile sonsuz
sayıdaki ölçümlerle varılabilecek
sonuçlar tahmin edilmiş olur.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
72
BİR ANALİZİN DOĞRULUĞU; GÜVENİRLİK
DERECESİ
Standart sapmanın hesaplanması analiz
sonucunun doğrululuğu hakkında bir tahmin
yapmayı sağlarsa da bulunan ortalama değer
gerçek değere ne kadar yakın olduğunu
bilinmez.
z Bu nedenle sonucun doğruluğu hakkında
deneysel ve matematiksel olmak üzere iki yolla
daha tahminde bulunulabilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
73
zMatematiksel yöntemde ise, gerçek
değerin ortalama değere yakın bir
aralıkta olduğu kabul edilir.
zOrtalama değere yakın bu aralığa
güven aralığı denir.
zBu aralık ne kadar geniş ise, gerçek
değerin bu aralığa düşme olasılığı o
kadar fazladır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
74
zBu aralığın sınırlarına güvenlik
sınırları denir.
zGerçek değerin yüzde olarak bu
aralıkta olma olasılığına ise
güvenirlik derecesi denir.
zGüvenirlik derecesi ile gerçek
değer arasındaki ilişki şu şekilde
verilebilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
75
zDeneysel yöntemde, analizi yapılan
maddenin, içindeki madde miktarı
bilinen saf örneği, aynı koşullarda
analiz edilir.
zBuradan bulunana hatanın diğer
analizlerde de yapıldığı kabul edilir.
zBu yöntemin olumsuz yönlerinden biri
örnekteki safsızlık maddelerinin
beklenenden daha fazla sonucu
etkileyebileceğidir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
76
⎛ S ⎞
T = X ± t⎜
⎟
⎝ N⎠
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
77
zBurada T gerçek değeri, X
ortalama değeri, S standart
sapmayı, N ölçüm sayısını
belirtir, t ise seçilen güvenirlik
derecesine ve ölçüm sayısına
bağlı bir sabittir. Çizelge 1’ de
değişik güvenirlik dereceleri için
t değerleri verilmiştir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
78
Örnek 6
zBir çinko filizin analiz sonuçları
yüzde çinko olarak şöyledir. 42.62,
43.12, 42.20, 43.22, 42.56, 42.86.
Bu analizin ortalama değerini,
standart sapmasını ve %95 ve
%99 güven aralığını bulunuz.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
79
Xi
42.62
43.12
42.20
43.22
42.56
42.86
xi − X
0.14
0.36
0.56
0.46
0.20
0.10
( xi − X ) 2
0.0196
0.1296
0.3136
0.2116
0.0400
0.0100
6
X = 42.76
∑ (x
S=
0.7244
= 0.38
5
M.DEMİR(ADU)
i =1
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
− X ) = 0.7244
2
i
80
z Çizelge 1’de altı ölçüm için %95 ve %99
güvenlik aralığı için t değerleri olan 2.57 ve
4.03 değerleri yerine konursa,
⎛ 0.38 ⎞
⎟⎟ = 42.76 m 0.40 ( %95 güvenle)
T = 42.76 m 2.57⎜⎜
⎝ 6 ⎠
⎛ 0.38 ⎞
T = 42.76 m 4.03⎜⎜
⎟⎟ = 42.76 m 0.62 ( %99 güvenle)
⎝ 6 ⎠
bulunur. Bunun anlamı; gerçek değerin %95 olasılıkla
42.76 ± 0.40 aralığında, %99 olasılıkla ise 42.76 ± 0.62
aralığında olduğudur.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
81
Çizelge.1
Çeşitli güven
aralıkları için t
değeri
M.DEMİR(ADU)
Güvenlik dereceleri
Ölçüm
sayısı (N)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
18
20
25
30
40
60
120
∞
%80
3.08
1.39
1.64
1.53
1.48
1.44
1.42
1.40
1.38
1.37
1.36
1.36
1.35
1.35
1.34
1.33
1.33
1.32
1.31
1.30
1.30
1.29
1.28
%90
%95
6.31
2.92
2.35
2.13
2.02
1.94
1.90
1.86
1.83
1.81
1.80
1.73
1.77
1.76
1.75
1.74
1.73
1.71
1.70
1.68
1.67
1.66
1.64
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
12.71
4.30
3.18
2.78
2.57
2.45
2.36
2.31
2.26
2.22
2.20
2.18
2.16
2.15
2.13
2.11
2.09
2.06
2.04
2.02
2.00
1.98
1.96
%97.5
25.5
6.21
4.78
3.50
3.16
2.97
2.84
2.75
2.69
2.65
2.59
2.55
2.53
2.51
2.49
2.46
2.43
2.39
2.36
2.33
2.30
2.27
2.24
%99
63.7
9.92
5.84
4.60
4.03
3.71
3.50
3.36
3.25
3.16
3.11
3.05
3.01
2.97
2.95
2.90
2.86
2.80
2.76
2.70
2.66
2.58
82
UÇ DEĞERLERİN ATILMASI
zBir ölçümde ortalama değere uzak olan
değerlerin ne yapılacağı, çoğu kez
sorun gibi görülür. Uç değerleri atarak
daha güvenli bir sonucun alınacağı
düşünülebilir. Hangi değerlerin
hesaplama dışında bırakılacağı
konusunda basit birkaç kuralı
uygulamak yeterlidir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
83
z Uç değerlerin atılabilmesi için belli nedenlerin
olması gerekir.
z Örneğin; ölçüm sırasında bürette bulunan
kirlilik, büretin akıtması, çözeltinin sıçraması
gibi nedenler uç değerlerin atılması için
yeterli nedenlerdir.
z Eğer belli bir neden yoksa yeni ölçümlerin
yapılması gerekir.
z Eğer yeni ölçümler için yeterli örnek
kalmamış ise, uç değerlerin atılıp
atılmayacağı konusunda bazı testleri
uygulamak gerekir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
84
Q Testi
zUç değerlerin atılıp atılmayacağı
konusunda bir çok istatistik testler
varsa da özellikle ölçüm sayısı az olan
analizlerde en iyi sonucu Q testi verir.
zQ, uç değer ile ona yakın olan değerler
arasındaki farkın ölçüm aralığına
bölümüdür.
zEğer bir ölçümün sonuçları büyüklük
sırasına göre dizilir ve son terime n
denirse
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
85
Q=
Atılmak istenen deger - atılmak istenen degere en yakın deger
ölçüm aralıgı
X m − X m −1
Q=
X n − X1
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
86
zolarak yazılabilir. Burada Xn en
büyük değeri, X1 en küçük değeri,
Xm atılmak istenen değeri, Xm-1
ise atılmak istenen değere en
yakın değeri tanımlamaktadır.
zBulunan değer çizelge 2’deki Q
değerlerinden büyük ise o ölçüm
atılabilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
87
Örnek.7
zBir demir filizi analizi sonuçları
yüzde demir olarak 32.42,
32.58, 32.36, 32.60, 32.00 ve
32.52 bulunmuştur.
zBuradaki 32.00 değerinin atılıp
atılamayacağım araştırınız.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
88
32.36 − 32.00 0.36
Q=
=
= 0.60
32.60 − 32.00 0.60
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
89
zÇizelge 2’ye bakılırsa 6 ölçüm
için Q değerinin 0.56 olduğu
görülür.
zBulunan Q değeri 0.56 dan
büyük olduğundan 32.00 değeri
%90 güvenlik için atılabilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
90
Çizelge 2 Çeşitli güvenlik dereceleri için Q değerleri
Ölçüm
sayısı
3
4
5
6
7
8
9
10
M.DEMİR(ADU)
Güvenlik derecesi
%90
%96
%99
0.94
0.76
0.64
0.56
0.51
0.47
0.44
0.41
0.98
0.85
0.73
0.64
0.59
0.54
0.51
0.48
0.99
0.93
0.82
0.74
0.68
0.63
0.60
0.75
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
91
Örnek 8
zBir bakır filiz analizi sonuçları
%53.13, %50.20 ve %51.23
olarak bulunmuştur.
zBu değerlerin herhangi birinin
atılıp atılamayacağını
araştırınız.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
92
51.23 − 50.20 1.03
=
= 0.94
Q=
51.23 − 50.13 1.10
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
93
zÇizelge 2’de 3 ölçüm için %90
güvenlik için Q değeri 0.94
olarak verilmiştir.
zBu durumda 51.23 değeri
istenilse atılabilir.
zAncak yeni bir ölçümün
yapılması daha uygundur.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
94
Örnek 9
zBir analizin sonuçları şu şekilde
bulunmuştur: 15.12, 16.82,
16.32, 16.22, 16.32, 16.02. bu
ölçümlerden herhangi birinin
atılıp atılamayacağını
araştırınız.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
95
zYukarıdaki analiz sonuçları
büyüklük sırasına göre dizilirse,
15.12, 16.02, 16.12, 16.22,
16.32, 16.32, 16.82 dizisi elde
edilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
96
15.12 ölçümü için :
16.02 − 15.12
Q=
= 0.53
16.82 − 15.12
Bu değer çizelgedeki 0.51 değerinden büyük
olduğundan 15.12 ölçümü atılabilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
97
16.82 değeri için :
16.82 − 16.32
Q=
= 0.625
16.82 − 16.02
Bu değer çizelgedeki altı ölçüm için verilen
0.56 değerinden büyük olduğu için 16.82
ölçümü atılabilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
98
16.02 ölçümü için :
16.12 − 16.02
Q=
= 0.333
16.32 − 16.02
Bulunan değer çizelgede beş ölçüm için
verilen 0.64 değerinden küçük olduğu için
atılmamalıdır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
99
16.32 ölçümü için :
16.32 − 16.32
0
Q=
=
=0
16.32 − 16.02 0.30
atılmamalıdır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
100
HESAPLAMA KURALLARI
z Bundan önceki bölümlerde de söylenildiği
gibi her ölçüm belli bir hata ihtimali taşır.
z Bir ölçümün sonucunu veren sayı onun
duyarlılığı hakkında bir fikir verir.
z Örneğin; bir büretteki okuma 28.6 şeklinde
yapılırsa buradaki 6’nın bir anlamı vardır.
z Çünkü bu rahatlıkla okunabilir.
z Ancak aynı okuma 28.63 şeklinde yapılırsa
son rakam olan 3 tahmin edilmiş olur.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
101
zBu okumayı farklı kişiler yapmış olsa bir
kısmının 28.64 olarak diğer bir kısmının
ise 28.62 olarak okuduğu görülür.
zO hâlde son rakam olan 3 kesin bir
rakam değildir, tahmin edilmiştir.
zBu tür ölçümlerde genel bir kural
uygulanır ve son rakamın tahmin
edildiği, kesin bir rakam olmadığı kabul
edilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
102
zSondan ikinci rakama ise kesin
gözüyle bakılır.
zÖrneğin; yukarıdaki 28.63
okumasında son rakam olan
3’ün kesin olduğu belirtmek
istendiğinde 28.630 olarak
yazılması gerekir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
103
zBir ölçümde virgülden sonraki
rakam sayısı bu ölçümün
duyarlılığı hakkında bir fikir verir.
zÖrneğin 12.6 gramlık bir tartım,
kaba bir terazide yapılmış olabilir.
zAncak 12.6276 gramlık bir tartım
mutlaka analitik bir terazide
yapılmıştır.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
104
zBir dizi ölçümde eğer
ölçümlerin duyarlılığı yani
virgülden sonraki basamak
sayısı birbirinden farklı ise, bazı
kuralları uygulayarak ölçümlerin
duyarlılığını aynı yapmak
gerekir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
105
Yuvarlama
zBir dizi ölçümün sonuçlarının virgülden
sonra aynı sayıda rakam içermesi yani
duyarlılığın aynı olması istendiğinde
yuvarlama yapılır.
zBunun için son rakam 5’ten büyük ise,
bundan önceki rakam bir arttırılır ve bu
rakam silinir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
106
zEğer son rakam 5’ten küçük ise bundan
önceki rakam hiç değiştirilmeden son
rakam silinir.
zSon rakamın 5 olması hâlinde ise,
bundan önceki yani sondan ikinci
rakama bakılır sondan ikinci rakam çift
ise, bu rakam hiç değiştirilmeden, tek
ise bir arttırılarak son rakam silinir.
zSıfır çift rakam kabul edilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
107
Örnek 10
zAşağıdaki sayıları virgülden
sonra bir basamak kalacak
şekilde kısaltınız. 65.734;
81.171; 76.456; 87.7; 18.25;
18.35; 18.50
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
108
zYukarıda söylenen kurallara
göre gerekli kısaltma yapılırsa
65.7; 81.2; 76.5; 87.7;
z18.2; 18.4 ve 18.0 sayıları elde
edilir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
109
Toplama ve Çıkarma
z Kesirli sayılarda toplama ve çıkarma
yaparken sayıdaki virgülden sonraki rakam
sayısını, yani ölçümün duyarlılığını,
duyarlılığı en az olanın düzeyine getirmek
gerekir.
z Aksi hâlde yapılan işlem bakkal terazisinin
tartımı ile bir analitik terazinin tartımını aynı
saymak olur.
z Örneğin; 43.46, 876.468 sayılarını
toplamadan önce sayıların duyarlılığını,
duyarlılığı en az olan 43.46’nın düzeyine
getirmek ve daha sonra toplama işlemini
yapmak gerekir.
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
110
Çarpma ve Bölme
zÇarpma ve bölme işlemlerinde çarpan
ve bölenlerin duyarlılığı ile çarpım ve
bölümün duyarlılığının aynı olması
gerekir.
zÖrneğin; 46.42x32.127 çarpımında
sonucun, çarpanlardan duyarlılığı en az
olanın düzeyinde yani virgülden sonra
iki basamak kalacak şekilde kısaltılması
gerekir.
z46.42x32.127 = 1491.3353 = 1491.34
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
111
ÇALIŞMA SORULARI
z 1. Bir bakır filizi ile yapılan üç analizde
%24.87, %24.93, ve %24.69 bakır
bulunmuştur. Bu filizdeki gerçek bakır
%25.06 olduğunu göre,
z Analizin ortalama değeri nedir?
z Mutlak hata nedir?
z Göreli hata binde olarak nedir?
z 2. Bir kireç taşındaki CaO ve Fe2O3 gerçek
değerleri %30.12 ve %2.69’dur. Ancak
analizin sonunda yazılan raporda %30.36
CaO ve %2.61 Fe2O3 olduğu belirtilmiştir.
Buna göre mutlak hata (binde olarak) nedir?
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
112
z3. Bir ayarlama işlemi sonunda
0.2114, 0.2101, 0.2116 ve 0.2115
değerleri bulunmuştur. Bu
değerlerden herhangi birini atmak
gerekir mi?
z4. Bir klorür analizde şu sonuçlar
bulunmuştur : 14.32, 14.75, 14.57 ve
14.80. Buna göre raporda klorür
miktarını ne şekilde yazmak gerekir?
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
113
z 5. Karbonun atom ağırlığı ile ilgili bir
çalışmada şu sonuçlar bulunmuştur:
12.0112, 12.6210, 12.0102, 12.0118,
12.0111, 12.0106, 12.0113, 12.0101,
12.0097, 12.0095 ve 12.0080.
z Bu analizin ortalaması nedir?
z Standart sapmanın mutlak değeri nedir?
z %95 güvenle karbonun atom ağırlığı nedir?
z Yukarıdaki değerlere ek olarak 12.0138
değeri bulunmuş olsa bu değeri atmak
gerekir mi?
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
114
z 6. Yedi ayrı sodyum okzalat örneğiyle potasyum
permanganat titre edilmiş ve şu sonuçlar
bulunmuştur: 0.2062, 0.2048, 0.2059, 0.2071,
0.2036, 0.2067 ve 0.2050. Bu sonuçların
ortalamasını, ortalama sapmasını ve standart
sapmasını hesaplayınız.
z 7. Bir demir filizinde gerçek demir miktarı %12.72’dir.
Yeni bir yöntemle yapılan altı ayrı tayinde sonuçlar
12.62, 12.58, 12.49, 12.65, 12.60 ve 12.56 olarak
bulunmuştur. Bu sonuçların ortalamasını ve hatanın
ortalamasını hesaplayınız. Bu hatanın nedenini
açıklamaya çalışınız.
z 8. Suyun sertlik tayini için yapılan altı ayrı analizin
sonuçları binde olarak şöyledir:
z
896.3, 888.4, 899.6, 872.9, 879.3 ve 882.6. Bu
ölçümlerin %90 ve %99 güvenlik
z
derecesi aralıklarını hesaplayınız, %95 güvenlik
sınırı nedir?
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
115
z 9. Bir organik bileşikteki karbon miktarının
tayini için sekiz farklı deney yapılmış ve
z
sonuçlar yüzde karbon olarak şu şekilde
bulunmuştur: 26.22, 26.72, 26.53, 27.26,
z
26.39, 26.64, 26.35 ve 26.47. Q testi
uygulayarak 27.26 ölçümünün atılıp
z
atılamayacağını araştırınız.
z 10. Bir bakır filizi örneğindeki bakır miktarı dört
ayrı deneyle bulunmuş ve sonuçlar
z
yüzde bakır olarak şu şekilde ifade
edilmiştir: 38.26, 39.49, 38.76 ve 39.10. Bu
z
değerlerden herhangi birinin atılması
gerekir mi?
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
116
z11. Bir analiz sonunda 0.0519,
0.0521, 0.0522 ve 0.0520 sonuçları
bulunmuştur.
zOrtalama sapma binde olarak
nedir?
zStandart sapma binde olarak
nedir?
zÖlçüm aralığı binde olarak nedir?
z%95 güvenlik aralığı nedir?
M.DEMİR(ADU)
2009-02-ANALİTİK VERİLERİN
DEĞERLENDİRİLMESİ
117