Mukavemet-II
Yrd.Doç.Dr. Akın Ataş
Bölüm 11
Enerji Yöntemleri
Kaynak: ‘Cisimlerin Mukavemeti’, F.P. Beer, E.R. Johnston, J.T. DeWolf,
D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok.
11.1 Giriş
Önceki bölümlerde çeşitli yükleme koşulları altında, kuvvetler ve
deformasyonlar arasındaki bağıntılar ile ilgilendik. Analizimiz iki temel
kavram üzerine kuruldu:
1. Gerilme kavramı,
2. Şekil değiştirme kavramı.
Üçüncü önemli kavram olan şekil değiştirme enerjisi kavramı bu
bölümde ele alınacaktır.
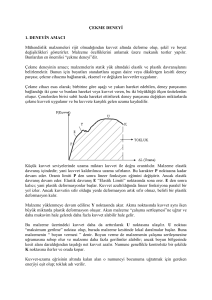
11.2 Şekil Değiştirme Enerjisi
Yükün
P
büyüklüğünün,
çubuğun
x
deformasyonuna
karşı
gelen
değerlerini
işaretleyerek yük-deformasyon diyagramı elde
edilir.
11.2 Şekil Değiştirme Enerjisi
Alan
Şekil Değiştirme
Enerjisi
P yükü çubuğa yavaşça uygulanırken, bu yük tarafından yapılan iş,
çubuğun deformasyonuyla ilişkili bir enerji artışı ortaya çıkarmalıdır.
Bu enerji, çubuğun şekil değiştirme enerjisi olarak adlandırılır.
İş ve enerji, kuvvet ve uzunluk birimleri çarpılarak elde edilir: N·m
(joule, J).
11.2 Şekil Değiştirme Enerjisi
Lineer ve elastik deformasyon halinde, yük-deformasyon
diyagramının karşı gelen kısmı, P = kx denklemli bir doğruyla temsil
edilebilir.
11.2 Şekil Değiştirme Enerjisi
Şekil değiştirme enerjisi kavramı
özellikle
darbe
yüklemelerinin
etkilerinin belirlenmesinde kullanışlıdır.
Çubuğun kazandığı Um maksimum şekil
değiştirme enerjisi, T kinetik enerjisine
eşittir.
Çubukta aynı şekil değiştirme enerjisini
üretecek olan Pm değeri belirlenip A
kesit alanına bölünürse, çubukta
meydana gelen gerilme değeri
belirlenebilir.
11.3 Şekil Değiştirme Enerjisi Yoğunluğu
Yük-deformasyon diyagramı ve şekil değiştirme
enerjisi denklemi, çubuğun boyutlarına bağlıdır.
Boyut etkisini yok etmek için, birim hacme düşen
şekil değiştirme enerjisi ele alınır.
Şekil Değiştirme
Enerjisi
Şekil Değiştirme Enerjisi
Yoğunluğu
Şekil değiştirme enerjisi yoğunluğu birimi, enerji birimlerinin hacim
birimlerine bölünmesiyle elde edilir: J/m3, kJ/m3, MJ/m3.
11.3 Şekil Değiştirme Enerjisi Yoğunluğu
Eğri altındaki alan (O-ε1), şekil değiştirme
enerjisi yoğunluğuna eşittir.
Yük kaldırılırsa, gerilme sıfıra düşer fakat
kalıcı deformasyon söz konusudur (εp).
Birim hacim başına düşen şekil değiştirme
enerjisinin sadece üçgensel alana karşı
gelen kısmı geri alınır.
Malzemenin
deformasyonu
sırasında
harcanan enerjinin kalanı, ısı enerjisi
şeklinde dışarı verilir.
11.3 Şekil Değiştirme Enerjisi Yoğunluğu
Şekil Değiştirme Enerjisi
Yoğunluğu
Dayanıklılık
Modülü
Kırılma
εR ile elde edilen ŞDEY, malzemenin
dayanıklılık modülü olarak bilinir.
Eğri altındaki tüm alana eşittir ve
malzemenin kırılması için gereken enerjiyi
temsil eder.
Buradan,
malzemenin
dayanıklılığının
kopma mukavemeti ile olduğu kadar
sünekliği ile de ilişkili olduğu görülür.
11.3 Şekil Değiştirme Enerjisi Yoğunluğu
Şekil Değiştirme Enerjisi
Yoğunluğu
Gerilme değeri, malzemenin orantı sınırı
içinde kalırsa,
Esneklik
Modülü
Esneklik modülü.
Esneklik modülü, OY doğru parçasının altındaki alana eşittir. Akma
olmaksızın, malzemenin soğurabildiği birim hacim başına düşen
enerjidir. Darbe yüküne direnme kapasitesi, esnekliğe bağlıdır.
11.3 Şekil Değiştirme Enerjisi Yoğunluğu
Dayanıklılık
Modülü
Kırılma
Demiryolu kavraması, büyük dayanıklılık modülüne sahip sünek
çelikten imal edilir.
11.4 Normal Gerilmeler için Elastik Şekil Değiştirme Enerjisi
Önceki kesimde ele alınan çubuk, düzgün yayılı σx gerilmelerine
maruz kaldığından, şekil değiştirme enerjisi yoğunluğu, çubuk
boyunca sabitti ve U/V olarak tanımlanabildi. Gerilme dağılımı
düzgün değilse, integral işlemi gerekir.
Sadece elastik deformasyonlar için geçerli olan bu ifade, cismin
elastik şekil değiştirme enerjisi olarak adlandırılır.
11.4 Normal Gerilmeler için Elastik Şekil Değiştirme Enerjisi
Eksenel Yüklemede Şekil Değiştirme Enerjisi.
Örnek 11.01
Alan
Bir çubuk, aynı malzemeden yapılmış ve aynı
uzunluklu, fakat farklı kesitli BC ve CD
parçalarından oluşmuştur. Çubuk bir P
merkezi eksenel yüküne maruz kaldığına
göre, çubuğun şekil değiştirme enerjisini, P, L,
E, CD parçasının A kesit alanı ve iki çapın n
oranı cinsinden ifade ederek belirleyiniz.
Örnek 11.01
Alan
Darbe yüklemesi gibi enerji soğurma kapasitesinin önemli olduğu
yüklere maruz elemanlarda, kesit alanındaki gereksiz değişimlerden
kaçınılmalıdır.
Örnek 11.02
P yükü, B noktasında, aynı malzemeden yapılmış ve
aynı A düzgün kesit alanına sahip iki çubuk
tarafından taşınmaktadır. Sistemin şekil değiştirme
enerjisini hesaplayınız.
Örnek 11.02
11.4 Normal Gerilmeler için Elastik Şekil Değiştirme Enerjisi
Eğilmede Şekil Değiştirme Enerjisi.
Kesme kuvvetinin etkisi ihmal edilmiştir.
Örnek 11.03
Sadece normal gerilmelerin etkisini hesaba
katarak, AB prizmatik ankastre kirişinin şekil
değiştirme enerjisini belirleyiniz.
Örnek 11.03
11.5 Kayma Gerilmeleri için Elastik Şekil Değiştirme Enerjisi
u şekil değiştirme enerjisi yoğunluğu, kayma gerilmesi-kayma şekil
değiştirmesi diyagramı altındaki alana eşittir.
11.5 Kayma Gerilmeleri için Elastik Şekil Değiştirme Enerjisi
Burulmada Şekil Değiştirme Enerjisi.
Örnek 11.04
Çap
Çap
Bir dairesel şaft, aynı malzemeden yapılmış ve
aynı uzunluklu, fakat farklı kesitli BC ve CD
parçalarından oluşmuştur. Şaft, D ucunda bir T
burulma çiftine maruz kaldığına göre, şaftın
şekil değiştirme enerjisini, T, L, G, küçük kesitin
J kutupsal eylemsizlik momenti ve iki çapın n
oranı cinsinden ifade ederek belirleyiniz.
Örnek 11.04
Çap
Çap
Örnek 11.05
Normal gerilmelerin ve kayma gerilmelerinin
etkisini hesaba katarak, AB dikdörtgen kesitli
ankastre kirişinin şekil değiştirme enerjisini
belirleyiniz.
Örnek 11.05
11.6 Genel Gerilme Halinde Şekil Değiştirme Enerjisi
Bir izotropik cismin elastik
deformasyonu halinde, ortaya çıkan altı σ-ε bağıntısının
her biri lineerdir ve şekil
değiştirme enerjisi yoğunluğu yanda verildiği gibi
hesaplanabilir.
11.6 Genel Gerilme Halinde Şekil Değiştirme Enerjisi
Verilen bir gerilme halinin, bir sünek malzemenin akmasına neden
olup olmadığını kestirmek için kullanılan ölçütlerden biri olan
maksimum distorsiyon enerjisi ölçütü, söz konusu malzemenin
distorsiyonu veya şeklindeki değişimle ilişkili birim hacim başına
enerjinin belirlenmesi üzerine kuruludur.
Bu yüzden, verilen bir noktadaki u şekil değiştirme enerjisi
yoğunluğunu, söz konusu noktada malzemenin hacmindeki bir
değişimle ilişkili uv parçası ve aynı noktada malzemenin distorsiyonu
veya şeklindeki değişimle ilişkili ud parçası olmak üzere, iki parçaya
ayıralım.
11.6 Genel Gerilme Halinde Şekil Değiştirme Enerjisi
uv ve ud’yi belirlemek için, göz önüne alınan noktada, asal
gerilmelerin ortalama değerini devreye sokalım.
Ayrıca,
Böylece, verilen gerilme
hali, şekilde gösterildiği
gibi
süperpozisyonla
elde edilebilir.
diyelim.
11.6 Genel Gerilme Halinde Şekil Değiştirme Enerjisi
(b)’deki gerilme hali, elemanın şeklini değil hacmini değiştirebilir. Öte
yandan,
bulunur. Bu, (c)’deki gerilmelerin bazılarının
çekme ve diğerlerinin basınç gerilmeleri olduğunu gösterir.
Dolayısıyla, bu gerilme hali elemanın şeklini değiştirebilir. Ancak
hacmini değiştiremez.
11.6 Genel Gerilme Halinde Şekil Değiştirme Enerjisi
Elemanın hacmindeki değişime karşılık gelen şekil değiştirme enerjisi
yoğunluğu uv, her bir asal gerilme yerine ortalama gerilme değeri
yazılarak elde edilir.
11.6 Genel Gerilme Halinde Şekil Değiştirme Enerjisi
Elemanın distorsiyonuna karşılık gelen şekil değiştirme enerjisi
yoğunluğu ud:
Düzlem gerilme halinde:
11.6 Genel Gerilme Halinde Şekil Değiştirme Enerjisi
Çekme deney numunesi özel halinde:
Genel gerilme halinde:
Örnek Problem 11.1
Üretim esnasında, AB çubuğu 120 in·lb’lik bir
elastik şekil değiştirme enerjisi kazanmalıdır.
Kalıcı deformasyona göre emniyet katsayısı
beş olacağına göre, E=29x106 psi alarak,
çeliğin gerekli akma mukavemetini belirleyiniz.
Örnek Problem 11.1
Esneklik
modülü
Örnek Problem 11.2
(a) Sadece eğilmeden kaynaklanan normal
gerilmelerin etkisini hesaba katarak,
gösterilen yükleme için, AB prizmatik
kirişinin şekil değiştirme enerjisini
belirleyiniz.
(b) Kiriş bir W10x45 profili ve P = 40 kips,
L = 12 ft, a = 3 ft, b = 9 ft ve E = 29x106 psi
olduğuna göre, şekil değiştirme enerjisini
hesaplayınız.
Örnek Problem 11.2
A’dan D’ye
B’den D’ye
Örnek Problem 11.2
a. Şekil Değiştirme Enerjisi.
b. Şekil Değiştirme Enerjisinin Hesaplanması.
11.7 Darbe Yüklemesi
Alan = A
Çubuk darbe etkisiyle deforme olurken,
çubuk içinde gerilmeler ortaya çıkar ve
bir maksimum değerine ulaşır.
Bir süre titreştikten sonra, çubuk
hareketsiz kalır ve tüm gerilmeler
ortadan kalkar.
Böyle olaylar dizisi darbe yüklemesi
olarak adlandırılır.
11.7 Darbe Yüklemesi
Alan = A
Gerilmenin
maksimum
değerini
belirlemek için, birçok basitleştirici
varsayım yapılır.
İlk olarak, çarpan cismin kinetik
enerjisinin tamamıyla yapıya aktarıldığı
varsayılır.
Uygulamada bu varsayım gerçekleşmez ve yapının tasarımının ihtiyatlı
olmasına yol açar.
11.7 Darbe Yüklemesi
Alan = A
Ayrıca, malzemenin statik deneyinden
elde edilen gerilme-şekil değiştirme
diyagramının, darbe yüklemesi halinde
de geçerli olduğu varsayılır.
Bu ifadeden, büyük V hacimli ve düşük E elastisite modüllü bir çubuk
seçmenin, verilen bir darbe yüklemesi için daha küçük bir gerilme
değeri ortaya çıkaracağı görülmektedir.
11.7 Darbe Yüklemesi
Alan = A
Birçok problemde, yapıdaki gerilme dağılımı düzgün değildir ve
yukarıdaki formül geçerli olmaz. Bu taktirde, darbe yüküyle aynı şekil
değiştirme enerjisi üretecek Pm statik yükünü belirlemek ve Pm’den,
yapıda ortaya çıkan en büyük gerilmenin karşı gelen σm değerini
hesaplamak uygundur.
Örnek 11.06
Alan = 4A
Bir v0 hızıyla hareket eden m kütleli bir
cisim, düzgün olmayan BCD çubuğuna B
ucundan çarpmaktadır. BC kısmının çapı
CD kısmınınkinin iki katı olduğuna göre,
çubuktaki gerilmenin σm maksimum
değerini belirleyiniz.
Örnek 11.06
Alan = 4A
Örnek 11.07
AB ankastre kirişinin serbest ucuna, h kadar
yükseklikten W ağırlıklı bir blok düşürülüyor.
Çubuktaki gerilmenin maksimum değerini
belirleyiniz.
Örnek 11.07
h mesafesinden düşerken, bloğun Wh potansiyel enerjisi kinetik
enerjiye dönüşür.
11.8 Darbe Yükleri için Tasarım
Um darbe yüklemesinin bir sonucu olarak çubuğa aktarılan enerji
miktarı, V ise çubuğun hacmi olmak üzere, düzgün kesitli bir
çubuktaki maksimum gerilme:
Bir darbe yüküne etkin olarak dayanacak şekilde tasarlanan bir yapı:
1. Büyük hacme sahip olmalıdır.
2. Düşük elastisite modüllü ve yüksek akma mukavemetli bir
malzemeden yapılmalıdır.
3. Gerilmelerin yapının tamamında mümkün olduğu kadar eşit
şekilde yayılmasını sağlayacak bir şekle sahip olmalıdır.
11.9 Tek Bir Yük Halinde İş ve Enerji
Düzgün kesitli bir çubuğun ucuna uygulanan bir P eksenel yükü tarafından
yapılan işe karşılık oluşan şekil değiştirme enerjisi:
Şekil Değiştirme
Enerjisi
Bir yapı veya eleman tek bir tekil yüke maruzsa, yük ve oluşan deformasyon
arasındaki ilişki biliniyorsa, elastik şekil değiştirme enerjisini belirlemek için
yukarıdaki denklem kullanılabilir.
11.9 Tek Bir Yük Halinde İş ve Enerji
11.9 Tek Bir Yük Halinde İş ve Enerji
Bir otomobilin bir bariyere çarpması, bir blok ve bir basit kirişten oluşan bir
model kullanılarak ele alınmaktadır.
Örnek 11.08
Bir v0 hızıyla hareket eden m kütleli bir
blok, AB prizmatik elemanına C orta
noktasından düz bir şekilde çarpmaktadır.
(a) Eşdeğer Pm statik yükünü,
(b) Elemandaki σm maksimum gerilmesini,
(c) C noktasındaki xm maksimum yer
değiştirmesini belirleyiniz.
11.10 Tek Bir Yük Halinde İş-Enerji Yöntemiyle Yer Değiştirme
P eksenel yükü veya M kuvvet çifti etkisindeki bir yapının şekil değiştirme
enerjisi aşağıdaki denklemlerden elde edilebilir:
Şekil değiştirme enerjisi biliniyorsa, aynı denklemler, yer değiştirme ve açı
değerlerinin belirlenmesi için de kullanılabilir.
Örnek 11.09
P yükü, B noktasında, aynı malzemeden
yapılmış ve aynı A düzgün kesit alanına
sahip iki çubuk tarafından taşınmaktadır.
B noktasının düşey yer değiştirmesini
belirleyiniz.
Örnek 11.03
AB ankastre kirişinin A ucunun yer
değiştirmesini, (a) sadece normal
gerilmeleri, (b) normal gerilmeleri ve
kayma gerilmelerini hesaba katarak
belirleyiniz.
Örnek Problem 11.3
Hareketsiz duran m kütleli D bloğu serbest
bırakılıyor ve bir h mesafesinden düşerek,
AB alüminyum kirişinin C orta noktasına
çarpıyor. E = 73 GPa alarak, (a) C noktasının
maksimum yer değiştirmesini, (b) kirişte
oluşan maksimum gerilmeyi belirleyiniz.
Örnek Problem 11.3
Ek D’den
1. Konum
2. Konum
*11.11 Çok Sayıda Yük Halinde İş ve Enerji
Kirişin şekil değiştirme enerjisi, P1 ve P2 tekil yüklerinin, kirişe C1 ve C2’de
yavaşça uygulanırken yaptıkları işe eşittir.
Ancak bu işi hesaplamak için, önce x1 ve x2 yer değiştirmelerini, P1 ve P2
yükleri cinsinden ifade etmeliyiz.
*11.11 Çok Sayıda Yük Halinde İş ve Enerji
Tesir katsayıları
Kirişe sadece P1’in uygulandığını varsayalım. C1 ve C2 yer değiştirmiştir
bunların yer değiştirmeleri P1 yükü ile orantılıdır.
*11.11 Çok Sayıda Yük Halinde İş ve Enerji
Tesir katsayıları
Kirişe şimdi de sadece P2’nin uygulandığını varsayalım.
*11.11 Çok Sayıda Yük Halinde İş ve Enerji
*11.11 Çok Sayıda Yük Halinde İş ve Enerji
P1 ve P2 tarafından yapılan işi ve dolayısıyla kirişin şekil değiştirme enerjisini
hesaplamak için, önce P1’in C1’de yavaş yavaş uygulandığını varsaymak uygun
olur.
C2, x21 kadar hareket ederken, P2’nin bir iş yapmadığına dikkat ediniz.
*11.11 Çok Sayıda Yük Halinde İş ve Enerji
Şimdi de P2’yi C2’de yavaşça uygulayalım. P2, C2’de yavaşça uygulanırken, P1’in
uygulama noktası, C1’’den C1’e x12 kadar hareket eder ve P1 yükü iş yapar.
*11.11 Çok Sayıda Yük Halinde İş ve Enerji
*11.11 Çok Sayıda Yük Halinde İş ve Enerji
*11.12 Castigliano Teoremi
*11.12 Castigliano Teoremi ile Yer Değiştirme
Örnek 11.12
AB ankastre kirişi, bir w düzgün yayılı
yükünü ve bir P tekil yükünü taşımaktadır. L
= 2 m, w = 4 kN/m, P = 6 kN ve EI = 5 MNm2
olduğuna göre, A’daki yer değiştirmeyi
belirleyiniz.
Örnek 11.13
AB ankastre kirişi, bir w düzgün yayılı
yükünü taşımaktadır. A noktasındaki yer
değiştirmeyi ve eğimi belirleyiniz.
Örnek 11.13
W250 x 22.3
w = 27 kN/m
b = 2.25 m
a = 1.35 m
L = 3.6 m
Gösterilen kiriş ve yükleme için, D noktasındaki yer değiştirmeyi
belirleyiniz. E = 200 GPa alınız.
Örnek 11.13
A’dan D’ye
B’den D’ye