3. BÖLÜM
øùLEMSEL KUVVETLENDøRøCøLERøN LøNEER
OLMAYAN UYGULAMALARI
øúlemsel kuvvetlendiriciler ve yarıiletken diyotlar, bipolar tranzistor gibi
devre elemanlarının birlikte kullanılmasıyla, karakteristikleri lineer olmayan çeúitli
türden devrelerin gerçekleútirilmesi mümkündür. Bunların arasında fonksiyon
üreteçleri, analog çarpma devreleri, do÷rultucular, gerilim karúılaútırıcılar, Schmitt
tetikleme devreleri gibi yapılar sayılabilir. Lineer olmayan devre uygulamaları,
endüstriyel elektronikte ölçü algılayıcıların karakteristiklerinin düzeltilmesi, çeúitli
ölçü düzenlerinin gerçekleútirilmesi gibi alanlarda yaygın olarak kullanılmaktadır.
Bu bölümde, iúlemsel kuvvetlendiricilerin temel lineer olmayan devre uygulamaları
ele alınarak incelenecektir.
3.1. øúlemsel kuvvetlendiriciler ve yarıiletken devre elemanlarının
birlikte kullanılmasıyla karakteristikleri lineer olmayan çeúitli türden
devrelerin gerçekleútirilmesi
3.1.1. Fonksiyon üreteçleri
Logaritma ve üs alma, üstel fonksiyon elde etme, sinüs ve kosinüs
fonksiyonları üretme, analog çarpma, bölme, karekök alma gibi iúlemleri
gerçekleútiren devre düzenleri fonksiyon üreteçleri olarak isimlendirilirler.
Logaritmik kuvvetlendiriciler
Çıkıú geriliminin giriú geriliminin logaritmasıyla orantılı bir de÷iúim
gösterdi÷i kuvvetlendirici yapıları logaritmik kuvvetlendiriciler olarak
isimlendirilirler. Logaritmik kuvvetlendiricilerin gerçekleútirilmesi amacıyla
bipolar tranzistor yahut diyot karakteristi÷inden yararlanılmaktadır. Yarıiletken
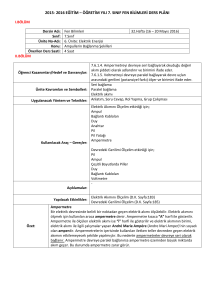
diyot ve bipolar tranzistor karakteristi÷inden yararlanılarak gerçekleútirilen basit iki
logaritmik kuvvetlendirici yapısı ùekil-3.1 'de verilmiútir.
ENDÜSTRøYEL ELEKTRONøK
56
D
R
+V I
R
+
+VO
+V I
+
T
+V O
ùekil-3.1. Basit logaritmik kuvvetlendirici yapıları.
Diyotlu devre için devrenin çıkıú gerilimini giriú gerilimine ba÷layan ba÷ıntı
aúa÷ıdaki yol izlenerek kolayca çıkartılabilir:
Yarıiletken diyodun akım - gerilim iliúkisi
§ §V D
· ·
I D = I S ¨ exp¨ .V T ¸-1¸
¹ ¹
© ©m
(3.1)
úeklindedir. Buradaki m büyüklü÷ü bir düzeltme çarpanı olup de÷eri 1 < m < 2
aralı÷ında yer alır. Geçirme yönünda kutuplama halinde diyot akımı
§ VD ·
¸
I D = I S .exp¨
© m.V T ¹
(3.2)
eúitli÷i ile verilir. Bu bölgede herhangi bir ID diyot akımı de÷eri için diyodun
uçlarındaki gerilim
§ID·
V D = m.V T . ln¨ ¸
© IS ¹
(3.3)
olur. Öte yandan, devreden hareket edilirse
V O = -V D , I D =
VI
R1
bulunur. Bunlar biraraya getirilirse, VI > 0 için
§ VI ·
¸
V O = -m.V T .ln¨
© I S . R1 ¹
(3.4)
olur. Ba÷ıntı 10 tabanına göre düzenlenirse
§ VI ·
¸
V O = -m.V T .ln10. log¨
© I S . R1 ¹
(3.5)
LøNEER OLMAYAN UYGULAMALAR
57
elde edilir. Diyot karakteristi÷i yardımıyla kurulan bu devrenin bazı sakıncaları
vardır:
1. Diyodun gövde direnci, logaritmik karakteristi÷i bozar;
2. m büyüklü÷ü akıma ba÷ımlıdır.
Diyodun gövde direnci üzerindeki gerilim düúümü, özellikle büyük akım
de÷erlerine gidildi÷inde, büyük de÷erler alır; bu gerilim düúümü ideal diyot
gerilimine seri gelece÷inden ve gerçek diyodun uçları arasında bu iki gerilimin
toplamı bulunaca÷ından, büyük akımlara do÷ru gidildi÷inde üstel karakteristi÷in
bozulaca÷ı açıktır.
Diyot karakteristi÷ini veren ba÷ıntıdaki m büyüklü÷ü diyot akımının bir
fonksiyonudur. Düúük akım seviyelerinde m büyüklü÷ü 2 de÷erine yaklaúır; orta
akımlar bölgesinde 1 de÷erini alır; yüksek akım seviyelerinde ise yine 2 de÷erine
gider.
Bu iki etken dikkate alındı÷ında, devrenin logaritmik karakteristi÷inin
do÷rulu÷u, ancak iki dekatlık bir de÷iúim aralı÷ı boyunca sa÷lanabilmektedir. m
çarpanının etkisi, bipolar tranzistorla kurulan ikinci devrede ortadan kalkar. Bir
bipolar tranzistorun kolektör akımı
ª§ V BE · § V BC ·º
-1¸ - ¨ exp
-1¸»
I C = I S .Ǭ exp
VT ¹ ©
V T ¹¼
©
(3.6)
biçiminde ifade edilir. VBC = 0 için kolektör akımı
§ V BE ·
-1¸
I C = I S .¨ exp
©
VT ¹
(3.7)
olur. Buradan hareketle baz-emetör gerilimi için
V BE = V T .ln
IC
IS
(3.8)
bulunur. Devrede
IC = I1 =
VI
R1
oldu÷u dikkate alınarak ba÷ıntılar biraraya getirilecek olursa, devrenin çıkıú
gerilimi için
ENDÜSTRøYEL ELEKTRONøK
58
V O = -V BE = -V T . ln
VI
I S . R1
(3.9)
eúitli÷i elde edilir. Diyot akımı ba÷ıntısından farklı olarak, bipolar tranzistorun
kolektör akımı ba÷ıntısında m büyüklü÷ü sabittir ve m = 1 olmaktadır. Bunun
ötesinde, kolektör akımı ba÷ıntısı, pA'lerden mA'lere kadar geçerlidir; dolayısıyla,
ikinci devrenin birinci devreye göre çok daha do÷ru sonuç verece÷i açıktır.
3. Bu iki devrede de çıkıú geriliminin sıcaklı÷a ba÷ımlılı÷ı çok fazladır. VT = kT/q
teriminin yanısıra, IS doyma akımı sıcaklı÷a
§ Eg ·
§ T ·
¸ . exp¨ - ¸
I S (T) = I S ( T nom ).¨
© T nom ¹
© k ¹
3
(3.10)
biçiminde bir ba÷ımlılık gösterir. Bu ba÷ıntıda T analizin yapılaca÷ı sıcaklık, Tnom
IS doyma akımının ölçüldü÷ü sıcaklık, Eg yarıiletken malzemenin eV olarak yasak
enerji bandı ve k da Boltzman sabitidir. IS doyma akımı her oC'de %7 oranında
artar. Buna göre
10
(1.07 ) = 2
olaca÷ından, her 10 oC de doyma akımı iki katına çıkacaktır. Bu ba÷ımlılık
I S (T) = I S ( T nom ).2(T -T nom )/ 10
(3.11)
úeklinde yazılabilir. Sıcaklık 20 oC den 50 oC ye yükseldi÷inde, VT ısıl gerilimi
%10 oranında artar. IS doyma akımı ise 8 katına çıkar. Logaritmik
kuvvetlendiricinin düzgün olarak çalıúabilmesi için bu etkinin azaltılması gerekir.
IS doyma akımının etkisi, iki logaritma alıcı devresinin çıkıúlarının farkı alınarak
elimine edilebilir. Sıcaklık kompanzasyonlu logaritmik kuvvetlendirici olarak
isimlendirilen bu yapı çeúitli úekillerde gercekleútirilebilir. Böyle bir devre yapısı
örne÷i ùekil-3.2'de verilmiútir.
ùekilden hareketle devrenin akım ve gerilimleri yazılırsa
§V BE 1 ·
¸
I C 1 = I S . exp¨
© VT ¹
LøNEER OLMAYAN UYGULAMALAR
R1
+V I
59
C
T 2 T1
R4
+
C
R3
+V O
+V1
R2
R1
+
+V ref
ùekil-3.2. Sıcaklık kompanzasyonlu logaritmik kuvvetlendirici yapısı.
§ V BE 2 ·
¸
I C 2 = I S . exp¨
© VT ¹
V 1 = V BE 1 - V BE 2
§V ·
I C1
= exp¨ 1 ¸
©V T ¹
I C2
V ref
VI
, IC2 =
I C1 =
R1
R1
R2
.V O
V1=
R2 + R3
elde edilir. Bunlar biraraya getirilirse
V O = -V T .
R2 + R3 § V I ·
. ln¨
¸
R2
©V ref ¹
(3.12)
elde edilir. (3.12) ba÷ıntısından fark edilebilece÷i gibi, çıkıú gerilimi IS doyma
akımına ba÷lı de÷ildir. R4 direnci çıkıú gerilimi ba÷ıntısına girmez. Bu direncin
de÷eri, üzerindeki gerilim düúümü OP2 iúlemsel kuvvetlendiricisinin çıkıú
geriliminin dalgalanma aralı÷ından yeteri kadar küçük olacak úekilde seçilir.
Yukarıda da belirtildi÷i gibi, doyma akımının çıkıú gerilimi üzerindeki
etkisi ortadan kalkmakta, sadece VT ısıl geriliminin etkisi bulunmakta, bu da çok
daha az bir sıcaklık ba÷ımlılı÷ı göstermektedir. R2 direnci için sıcaklık katsayısı
TCR = %0.3/oK olan bir direnç kullanılırsa, VT ısıl geriliminin etkisi de kompanze
edilebilir.
Genellikle, logaritmik kuvvetlendiricinin karakteristi÷inin 1V/dek'lık bir
e÷im göstermesi istenir. Bu de÷iúimi sa÷layacak direnç oranı hesaplansın.
ENDÜSTRøYEL ELEKTRONøK
60
V O = -V T
§ VI ·
§ VI ·
R2 + R3 1
log¨
¸= -1V.log¨
¸
R2 loge © V ref ¹
©V ref ¹
eúitli÷inden hareketle, VT = 26 mV için
R2 + R3 1V. loge
= 16.7
=
VT
R3
bulunur. Bu direnç oranı
R2 = 1k: , R3 = 15.7k:
alınarak sa÷lanabilir. Fark edilebilece÷i gibi R2 << R3 olmaktadır.
+VCC
R3
T1
R1
R6
+
+V I
R4
T2
+
-
OP2
OP1
+V O
R5
R2
ùekil-3.3. Di÷er bir logaritmik kuvvetlendirici yapısı.
Di÷er bir logaritmik kuvvetlendirici yapısı ùekil-3.3'de görülmektedir. Bu
yapı, önceki yapıya benzer özellikler gösterir. Devreden hareket edilirse
V BE 1 - V BE 2 = -V T . ln
II
I3
bulunur. Öte yandan OP2 ile kurulan kuvvetlendirici katın kazancı
KVf =
R4 + R5
R5
oldu÷undan, devrenin çıkıú gerilimi için
R4 + R5 I I
ln
R5
I3
R4 + R5
VI
ln
V O = -V T
R5
R1 . I 3
V O = -V T
(3.13)
LøNEER OLMAYAN UYGULAMALAR
61
ba÷ıntısı elde edilir. VO = 0 noktası I3 akımı ile belirlenir. Bu akımın de÷eri de R3
direnci ile ayarlanır. I3 = II de VBE1 = VBE2 olur. VBE gerilimlerinin sıcaklıkla
de÷iúimleri, bu devrede birbirlerini kompanze ederler. Devredeki R1 direncinin
de÷eri T1 tranzistorunun kolektör akımına ve giriú geriliminin de÷iúim aralı÷ına
ba÷lıdır. Giriú geriliminin de÷iúim aralı÷ı bir kaç 10V mertebesindedir; alabilece÷i
minimum de÷er ise mikrovoltlar mertebesine inmektedir. Devrede görülen R6
direnci, T1 tranzistorunun OP1 iúlemsel kuvvetlendiricisinin çevrim kazancını
yükseltip kararsızlı÷a yol açmaması için kullanılmıútır; böylece, kazanç R1/R6 ile
sınırlanmaktadır.
Üstel fonksiyon devresi, ters logaritmik kuvvetlendirici
ùekil-3.1'den izlenebilece÷i gibi, basit logaritmik kuvvetlendirici devresi,
faz döndüren kuvvetlendirici yapısında geribesleme yolu üzerine lineer olmayan
eleman yerleútirilmesiyle kurulmuútur. Bu yapıda lineer olmayan elemanın yerinin
de÷iútirilmesiyle ters logaritmik kuvvetlendirici devresi kolayca gerçekleútirilebilir.
Ters logaritmik kuvvetlendirici devresi ùekil-3.4'de verilmiútir.
R
1
T
+V
I
+
+V
O
ùekil-3.4. Basit ters logaritmik kuvvetlendirici.
Bu devrede tranzistorun kolektör akımı
§ V BE ·
§ VI·
¸= I S . exp¨ - ¸
I C = I S .exp¨
© VT ¹
© VT¹
oldu÷undan, devrenin çıkıú gerilimi
§ VI·
V O = I S . R1 .exp¨ - ¸
© VT¹
(3.14)
úeklindedir. IS doyma akımının sıcaklı÷a ba÷ımlılı÷ı ùekil-3.4'deki basit ters
logaritmik kuvvetlendiricide de sorun yaratır. Daha önce logaritmik
kuvvetlendiricide yapıldı÷ı gibi, fark kuvvetlendiricisi yapısı kullanılarak devrenin
sıcaklık kararlılı÷ı iyileútirilebilir. øki iúlemsel kuvvetlendirici ve fark
ENDÜSTRøYEL ELEKTRONøK
62
kuvvetlendiricisi kullanılarak gerçekleútirilen ters logaritmik kuvvetlendirici
devresi ùekil-3.5'de verilmiútir.
C
R1
+V ref
+V1
T2 T1
R2
R1
R3
+
OP1
+
+VI
R4
+V O
OP2
ùekil-3.5. Sıcaklık kompanzasyonlu ters logaritmik kuvvetlendirici.
Devrede
V ref
I C1
V1
VO
= exp
, I C1 =
, IC2 =
R1
I C2
VT
R1
R2
V1=
VI
R2 + R3
oldu÷undan hareket edilirse, çıkıú gerilimi için
§ R2 V I ·
¸
V O = V ref . exp¨
© R2 + R3 V T ¹
(3.15)
eúitli÷i elde edilir. (3.15) ba÷ıntısından görülebilece÷i gibi, sonuç IS doyma akımını
içermemektedir. Devredeki R4 direnci, T1 ve T2 tranzistorlarının akımını
sınırlamaya yarar, ancak bu direnç ba÷ıntılarda görülmedi÷i için de÷eri çıkıú
gerilimini etkilemez.
Devre uygulamalarında, ço÷unlukla, 1V'luk bir giriú gerilimi de÷iúimi için
bir dekatlık bir çıkıú gerilimi de÷iúimi istenir. Bu úartı yerine getiren direnç oranını
belirlemek üzere ba÷ıntı düzenlenirse
R2
VI
VI
V O = V ref .10 R2+R3 V T .log e = V ref .10 1V
elde edilir. VT = 26 mV için
LøNEER OLMAYAN UYGULAMALAR
63
R2 + R3 1V. log e
= 16.7
=
VT
R2
olur.
Üs alma devresi
y = xa
(3.16)
úeklinde üs almanın gerekli oldu÷u devre uygulamalarında, x > 0 için logaritmik
kuvvetlendirici ve ters logaritmik kuvvetlendirici yardımıyla bu iúlem kolayca
yerine getirilebilir. Devrenin blok úeması ùekil-3.6'da verilmiútir. Blok úemadan
hareketle devrenin çıkıú gerilimi hesaplanırsa
§
VI
¨ a.V T .lnV ref
V O = V ref .exp¨
VT
¨
©
·
a
¸
§ VI ·
¸= V ref .¨
¸
©V ref ¹
¸
¹
(3.17)
bulunur. Ba÷ıntı, sadece pozitif giriú gerilimleri için geçerlidir; zira logaritma
pozitif gerilimler için tanımlıdır.
+V I
VT ln (V I /V ref )
V1
(-a)
V2
Vref exp ( V2/VT )
+V O
ùekil-3.6. Üs alma devresi.
3.1.2. Analog çarpma devreleri
Uygulamada kullanılan analog çarpma devreleri, ço÷unlukla, Gilbert
dörtlüsü yapısındadır. Ancak, Gilbert dörtlüsü ilkesine göre çalıúan analog çarpma
devreleri küçük genlikli iúaretler için lineer çarpma iúlemini yerine getirirler.
Büyük genlikli giriú iúaretleri uygulanması halinde ise nonlineer bir çarpma iúlemi
elde edilir. Büyük genlikli iúaretlerin çarpılması istendi÷inde, Gilbert dörtlüsünün
ENDÜSTRøYEL ELEKTRONøK
64
karakteristi÷i lineerleútirilebilir. Ancak, bu defa da küçük genlikli iúaretler için
devrenin karakteristi÷i kötüleúir.
Gilbert dörtlüsünün bu sakıncası, iúlemsel kuvvetlendiricilerle logaritmik
çarpma devreleri yardımıyla giderilebilir. Logaritmik kuvvetlendiricilerin biraraya
getirilmesi ile çarpma ve bölme iúlemlerinin gerçekleútirilmesi mümkündür. Bunun
için giriú iúaretlerinin logaritmalarının toplanıp çıkarılması gerekir. Bu tür yapıların
çalıúma ilkesi
x. y
= exp [ ln x+ ln y- ln z ]
z
denklemine dayanmaktadır. Bu fonksiyon, üç logaritmik kuvvetlendirici, bir ters
logaritmik kuvvetlendirici ve bir toplama-çıkarma devresi yardımıyla sa÷lanabilir.
Ters logaritmik kuvvetlendiricideki fark kuvvetlendiricisinin giriúleri, fark alma
iúlemi için kullanılmaktadır. Devre yapısı ùekil-3.7'de verilmiútir.
R1
RE
+
+V
X
R1
T3 T4
C
+
+VO
T1
R1
+VY
V1
V2
RE
RE
T2
C
R1
+
+
+VZ
ùekil-3.7. Analog çarpma-bölme devresi.
Devredeki V1 ve V2 gerilimleri hesaplanıp, buradan hareketle çıkıú gerilimi
hesaplanırsa
V1
V T .ln
Vy
I S . R1
(3.18)
LøNEER OLMAYAN UYGULAMALAR
V 2 = -V T . ln
65
VZ
I S . R1
(3.19)
§V 2 - V 1 · V x .V y
¸=
V O = V x .exp¨
© VT ¹ VZ
(3.20)
bulunur. Ba÷ıntıdan fark edilebilece÷i gibi, çıkıú gerilimi ifadesinde tranzistorların
IS doyma akımları ve VT ısıl gerilimi yer almamaktadır; dolayısıyla, sıcaklı÷a
ba÷ımlı terim bulunmamaktadır. Dolayısıyla, ayrıca sıcaklık kompanzasyonu
gerekli de÷ildir. Devrenin istenen özellikleri sa÷laması için gerekli úart, dört
tranzistorun da eú olmaları ve aynı özellikleri göstermeleridir.
Yapının en önemli sakıncası ise, giriú gerilimlerinin daima pozitif olması
zorunlulu÷udur. Dolayısıyla, bu tür bir analog çarpma devresi tek bölgeli bir
analog çarpma devresi olarak çalıúır. Ancak, giriú gerilimlerinin her iki yönde de
de÷iúebilmelerini sa÷lamak üzere, devreye ek alt devreler eklenebilir. Bunu
sa÷lamak üzere baúvurulabilecek bir yol, giriú iúaretlerini presizyonlu do÷rultucu
devrelerinin giriúlerine uygulamak ve bunların çıkıú iúaretlerini ùekil-3.7'deki
devrenin giriúlerine uygulamaktır. Böylece, çarpma devresinin giriú gerilimlerinin
sadece pozitif olmaları sa÷lanabilir. Bazı uygulamalar açısından (etkin de÷er alma
vb) bu tür bir çözüm yarar sa÷lamakla birlikte, devrenin çıkıú geriliminin sadece
tek yönde de÷iúebilmesi, bu yöntemin önemli eksiklerinden birini oluúturur.
Giriú iúaretlerinin do÷rultucular üzerinden devreye uygulandı÷ı bir analog
çarpma devresinin blok úeması ùekil-3.8'de verilmiútir.
'
+V X
+V
x
'
+VY
+V O
+V Y
ùekil-3.8. Giriú iúaretlerinin do÷rultulması yöntemi.
ENDÜSTRøYEL ELEKTRONøK
66
Di÷er bir yol, Vx ve Vy gerilimlerine sabit de÷erli Vxk ve Vyk gerilimlerini
eklemek ve bileúke giriú gerilimlerinin her úart altında izin verilen bölge içerisinde
kalmasını sa÷lamaktır. Bu durumda
VO =
(V x +V xk ).(V y +V yk )
E
V x .V y
V yk
V xk .V yk
V xk
=V O .V y .V x E
E
E
E
(3.21)
olur. østenen çarpma iúleminin yerine getirilebilmesi için çıkıú geriliminden iki
sabit gerilimin çarpımının ve her bir giriú gerilimiyle orantılı iki gerilimin
çıkartılması gerekir. Bunun için gereken devrenin blok úeması ùekil-3.9'de
verilmiútir.
V
+V
-1
0,5
X
0,5
E
+V Y
1>0
4
V1 . V2
_______
E
0,5
0,5
E
-1
Vx .V Y
+V O = ______
E
-1
V 2 >0
ùekil-3.9. Dört bölgeli analog çarpma devresi.
Sabit gerilimler ve katsayılar, giriú gerilimlerinin tüm de÷iúim bölgesi
boyunca analog çarpma iúlemi sa÷lanabilecek úekilde seçilirler. Buna göre Vx
gerilimi için
- E d V x d E V 1 = 0,5.V x +0,5.E alınırsa, V1 gerilimi (analog çarpma devresi
hücresinin giriú gerilimi)
0 =d V 1 d E
olur. Benzer úekilde Vy giriú gerilimi için de
LøNEER OLMAYAN UYGULAMALAR
67
-E d V y d E
V 1 = 0,5.V y +0,5.E
úartı bulunmaktadır. Bu durumda, çıkıú gerilimi de
1
1
.(V x + E). .(V y + E)
V x .V y
2
2
- V x -V y - E =
VO = 4
E
E
(3.22)
olur.
3.1.3. Bölme ve karekök alma devreleri
+V Z
VO .V Z
_______
E
+
+V X
+VO
ùekil-3.10. Bölme devresi.
Analog çarpma devresini iúlemsel kuvvetlendirici ile birlikte kullanarak
bölme devresi gerçekleútirilebilir. Bu tür bir bölme devresi ùekil-3.10'da
görülmektedir. Bu devrede giriú iúaretlerinden biri analog çarpma devresinin bir
giriúine, di÷er giriú iúareti ise iúlemsel kuvvetlendiricinin faz döndürmeyen giriúine
uygulanmıútır. Çıkıú iúareti analog çarpma devresinin di÷er giriúine, analog çarpma
devresinin çıkıúı da iúlemsel kuvvetlendiricinin faz döndüren giriúine verilerek
geribeslemeli bir düzen oluúturulmuútur. øúlemsel kuvvetlendiricinin iki giriú
geriliminin eúit olmaları nedeniyle
Vx=
V O .V z
E
eúitli÷i sa÷lanaca÷ından, devrenin çıkıú gerilimi
ENDÜSTRøYEL ELEKTRONøK
68
V O = E.
Vx
Vz
(3.23)
olur. Görüldü÷ü gibi, çıkıú gerilimi iki giriú geriliminin oranı ile orantılı
olmaktadır. Vz > 0 için devre düzgün çalıúır. Vz < 0 durumunda ise geribesleme
pozitif geribeslemeye dönüúür ve kararsızlık sorunu ortaya çıkar.
2
VO
___
E
+
+VO
+V I
ùekil-3.11. Karekök alma devresi.
Yapı üzerinde yapılacak basit bir de÷iúiklikle, devre kolayca karekök alma
devresi haline getirilebilir. Bu tür bir karekök alma devresi ùekil-3.11'de
verilmiútir. Bu devrede analog çarpma devresinin her iki giriúine de VO çıkıú
gerilimi uygulanmıútır. Bu durumda iúlemsel kuvvetlendiricinin giriú gerilimlerinin
eúit olmaları gerekti÷inden hareket edilirse, çarpma devresinin çıkıú gerilimi ile VI
gerilimleri eúit olacaklarından
VI =
V 2O
E
ve buradan da devrenin çıkıú gerilimi için
V O = E.V I
(3.24)
ba÷ıntısı bulunur. Devre pozitif giriú ve çıkıú gerilimlerinde düzgün çalıúır. Negatif
giriú gerilimlerinde ise çevrim kazancı iúaret de÷iútirir, pozitif geribesleme oluúur,
bunun sonucunda çıkıú gerilimi negatif kayna÷a giderek kenetlenir. Bu olayın
ortaya çıkmaması için diyotlu kenetleme vb önlemlerin alınması gerekmektedir.
Karekök alma devreleri, lineer olmayan karakteristiklerin düzeltilmesi,
etkin de÷er ölçü düzeni gerçekleútirilmesi gibi uygulamalarda yaygın olarak
kullanılmaktadır.
LøNEER OLMAYAN UYGULAMALAR
69
3.1.4. AC-DC çeviriciler
Presizyonlu do÷rultucular
Faz döndürmeyen do÷rultucu
Diyotlu do÷rultucularda eúik gerilimi ve diyot iç direncinin getirece÷i
sorunları gidermek üzere, iúlemsel kuvvetlendiricilerin özelliklerinden yararlanarak
presizyonlu do÷rultucu devreleri kurmak ve bunları çeúitli ölçü düzenlerinde
kullanmak mümkündür. Bu tür bir do÷rultucu gerçekleútirmek üzere, iúlemsel
kuvvetlendirici faz döndüren veya faz döndürmeyen kuvvetlendirici yapısında
çalıúırken, geribesleme yolu üzerine bir diyot yerleútirilmektedir. Her iki yapının
çalıúması da aynı ilkeye dayanmakla birlikte, aralarında VO çıkıú geriliminin yönü,
devrenin giriú direnci ve frekans cevabı açısından üç temel fark bulunmaktadır.
Faz döndürmeyen kuvvetlendirici yapısında kurulan presizyonlu
do÷rultucu devresi ùekil-3.12'de verilmiútir. ùekilde iúlemsel kuvvetlendiricinin
çıkıú gerilimi VO' sembolü ile devrenin çıkıú gerilimi ise VO ile belirtilmiútir.
VO' > 0 oldu÷u sürece diyot iletimdedir ve yapı geribeslemeli bir
kuvvetlendirici olarak çalıúır. Kuvvetlendiricinin gerilim kazancı
KVO =
R1 + R 2
olur.
R1
R2
VO
D
+
V
'
VO
I
R
1
ùekil-3.12. Faz döndürmeyen kuvvetlendirici yapısı ile presizyonlu do÷rultucu devresi.
VO' < VJ oldu÷u sürece diyot tıkalıdır; dolayısıyla geribesleme çevrimi
etkisiz kalır. øslemsel kuvvetlendiricinin VO' çıkıúında yüksüz (geribeslemesiz)
haldeki kazanç elde edilir. Bu, iúlemsel kuvvetlendiricinin açık çevrim kazancına
ENDÜSTRøYEL ELEKTRONøK
70
eúit oldu÷undan, küçük de÷erli negatif bir giriú gerilimi, VO' çıkıú gerilimini
iúlemsel kuvvetlendiricinin VOmin sınır de÷erine getirmeye yeterli olur. Diyodun
kesimde olması durumu için devrenin VO çıkıú gerilimi VO = 0 olur.
øúlemsel kuvvetlendiricinin açık çevrim kazancı yeteri kadar büyükse, çok
küçük de÷erli bir pozitif giriú gerilimi iúlemsel kuvvetlendiricinin VO' çıkıú
gerilimini diyodun VJ eúik gerilimine getirmeye yeterlidir. Bu nedenle, do÷rultucu
devresinin eúik gerilimi de çok düúük olur. Devrenin çıkıú gerilimi
R1 + R 2
(V O'-V J )
R1 + R 2 + r
(3.25)
ª
º
VO ' = KV . «V I - R1 V O »
R1 + R 2 ¼
¬
(3.26)
VO =
olur. Burada VO' büyüklü÷ü
ba÷ıntısıyla ifade edilmektedir. Ba÷ıntılar biraraya getirilirse, VI > 0 için E =
R1/(R1+R2) olmak üzere
VO =
ª R1 + R 2
R1 + R 2
VJ º
VI«
§
1 ·
r ¬ R1
KV . E »¼
¸+
( R1 + R2 ).¨1+
© KV . E ¹ K V . E
(3.27)
elde edilir. E.KV >> 1 olması durumunda (3.27) ba÷ıntısı
VO =
R1 + R 2
r
R1 + R 2 +
KV . E
ª R1 + R 2
VJ º
.«
VI¬ R1
KV . E »¼
(3.28)
úeklini alır. Görülece÷i gibi, faz döndürmeyen kuvvetlendirici yapısındaki
do÷rultucunun gerilim kazancı
KVf =
R1 + R 2
R1
LøNEER OLMAYAN UYGULAMALAR
71
J
ùekil-3.13. Basit diyotlu do÷rultucu.
de÷erini almaktadır. Devrenin özellikleri ùekil-3.13'deki basit diyotlu
do÷rultucunun özellikleri ile karúılaútırılırsa, basit diyotlu do÷rultucuda VI > VJ
için çıkıú gerilimi
VO =
RL
.(V I - V J )
RL + r
(3.29)
úeklindedir. Burada r direnci devredeki diyodun seri direncini, VJ büyüklü÷ü de
diyodun eúik gerilimini göstermektedir.(3.28) ve (3.29) ba÷ıntıları karúılaútırılırsa,
iúlemsel kuvvetlendirici ile kurulan presizyonlu do÷rultucuda eúik geriliminin ve
seri direncin E.KV çevrim kazancı kadar küçülmüú oldu÷u kolayca görülebilir.
Devrenin VO -VI ve VO' -VI geçiú karakteristikleri ùekil-3.14'de verilmiútir.
Ortalama de÷er do÷rultucusu olarak kullanılma ve sinüs biçimli bir giriú
iúareti uygulanması durumunda, devrenin ortalama çıkıú gerilimi
VO =
R1 + R 2 V P
. .
S
R1
R1 + R 2
r
R1 + R 2 +
KV . E
ª S
VJ º
.«1- .
¬ 2 KV .V P »¼
(3.30)
olur. Bu ba÷ıntıda VP büyüklü÷ü VI giriú geriliminin tepe de÷eridir. Ba÷ıntıdan
fark edilebilece÷i gibi, ortalama de÷er do÷rultucusu olarak kullanılma durumunda,
çıkıú iúaretinde oratya çıkacak ba÷ıl hata
h=-
S
VJ
2 KV .V P
.
(3.31)
olur.
Alçak frekanslarda KV = KV0 olaca÷ından, kazanç çok büyük de÷erlidir; bu
nedenle h ba÷ıl hatası bu frekanslarda ihmal edilebilir. Dolayısıyla, alçak
frekanslarda do÷ruluk sadece iúlemsel kuvvetlendiricinin dengesizlik gerilimine ve
sürüklenmesine ba÷lı olur.
ENDÜSTRøYEL ELEKTRONøK
72
J
ùekil-3.14. Faz döndürmeyen do÷rultucunun VO - VI ve VO'-VI geçiú karakteristikleri.
Yapı yüksek frekanslarda kullanılmaya elveriúli de÷ildir. Bunun nedeni úu
úekilde açıklanabilir:
Diyot ileri yönde kutuplandı÷ında, devrenin kazancı
K VfO =
R1 + R 2
R1
de÷erini alır. Ancak, devrenin kararlılı÷ının sa÷lanması gerekti÷inden, iúlemsel
kuvvetlendiriciye frekans kompanzasyonu uygulanması zorunlu olur; bu nedenle,
çıkıú iúaretinin de÷iúim hızı, iúlemsel kuvvetlendiricinin YE yükselme e÷imi ile
sınırlıdır. Küçük de÷erli bir negatif gerilimin kuvvetlendiriciyi negatif yönde
doymaya sürdü÷ü varsayılsın. Daha sonra uygulanan ve negatif de÷erden pozitif
de÷ere do÷ru de÷iúen bir VI giriú gerilimi ile kuvvetlendiricinin sürüldü÷ü kabul
edilsin. Bu durumda iúlemsel kuvvetlendiricinin VO' çıkıú gerilimini sınırlayan etki
sadece YE yükselme e÷imi de÷ildir; diyodun ts toparlanma süresinin de etkisi
vardır. Diyot toparlanmadan önce, iúlemsel kuvvetlendiricinin etkisiyle
t1 =
V J - V Omin
YE
(3.32)
LøNEER OLMAYAN UYGULAMALAR
73
VI
t
VO'
VJ
t1
t
arctan SR
VOmin
ts
ùekil-3.15.Faz döndürmeyen do÷rultucunun çıkıú geriliminin zamana göre de÷iúimi.
süresi geçer. Bu sürenin diyodun toparlanma süresine eklenmesi gerekir. Devrenin
gerilim-zaman diyagramı ùekil-3.15'de verilmiútir. Gerilim diyagramında
kaybedilen alan hesaplanırsa
V J V Omin ·
2.S .V OP t 2
V OP t 1 2.S
V OP .Z 2 §
sin
.dt
|
t.dt
=
.
t
³
³
¨
¸
s+
2
0
T 0
T
4S ©
YE ¹
T
2
(3.33)
bulunur. Görüldü÷ü gibi, bu alan giriúe uygulanan iúaretin frekansının ikinci
kuvveti ile artmaktadır. Frekansa ba÷lı ba÷ıl hata
h2
VJ VO min º
1 ª
Z 2 «t s »
4 ¬
YE
¼
2
(3.34)
olur. Hatanın elimine edilmesi için negatif yönde olası doymanın önlenmesi ve VO'
geriliminin sınırlanması gerekir.
ENDÜSTRøYEL ELEKTRONøK
74
Faz döndüren do÷rultucu
Do÷rultucu devresi faz döndüren kuvvetlendirici yapısı yardımıyla da
kurulabilir. Yüksek frekans cevabı açısından bu yapı faz döndürmeyen do÷rultucu
yapısına göre daha üstündür. Bunun baúlıca iki nedeni vardır:
Birincisi, devreye uygulanan geribesleme VI giriú geriliminin tek
yarıperiyodu ile sınırlı de÷ildir.
økincisi, bu yapıda devreye uygulanan kompanzasyon daha büyük bir
yükselme e÷imi elde edilmesini mümkün kılmaktadır.
Faz döndüren do÷rultucu devresi ùekil-3.16'da verilmiútir. ùekil3.16a’daki devrede D1 diyodu biri iletim yönünde kutuplandı÷ında, VO' > VJ úartı
altında devre geribeslemeli kuvvetlendirici olarak çalıúır. Böylece devrenin kazancı
KVfO = -
R2
R1
olur. VO' < VJ oldu÷unda geribesleme ortadan kalkar ve devre açık çevrimde
çalıúır. KVO çok büyük de÷erli oldu÷undan, çok küçük bir pozitif yahut negatif
gerilim VO' çıkıú gerilimini diyodların VJ eúik gerilimine getirir; dolayısıyla çok
küçük bir eúik gerilimi elde edilece÷i açıktır.
ùekil-3.16’daki devrelerle pozitif yahut negatif yönde do÷rultma
yapılabilir.
ùekil-3.16a’daki devrede D2 diyodu iletim yönünde kutuplandı÷ında
devrenin çıkıú gerilimi
VO =-
R2
.V I
R1
olur. Bu úartın yerine gelebilmesi için ise devrenin giriú geriliminin VI < 0 olması
gerekir. Pozitif giriú gerilimlerinde D2 diyodu tıkama yönünde kutuplanır ve VO = 0
olur. Bu durumda D1 diyodu iletime geçer ve geribesleme yolu oluúturarak
kuvvetlendiricinin negatif yönde doymaya gitmesini önler. Devrenin çalıúmasına
iliúkin ba÷ıntılar aúa÷ıda verilmiútir.
LøNEER OLMAYAN UYGULAMALAR
75
R2
R1
+ VO
D2
D1
+
+VI
R 1 // R 2
(a)
+VO
R1
R2
D1
D2
+
+VI
R 1 // R 2
(b)
ùekil-3.16. Faz döndüren kuvvetlendirici yapısında çalıúan do÷rultucu devresi; a) negatif
giriú iúaretleri için do÷rultucu, b) pozitif giriú iúaretleri için do÷rultucu.
VO =-
R2
V I , V I <0
R1
VO =0 , V I >0
Benzer úekilde hareket edilirse, ùekil-3.16b’deki devre için de
VO =-
R 2c
V I , V I >0
R1
VO =0 , V I <0
bulunur.
ENDÜSTRøYEL ELEKTRONøK
76
ùekil-3.16a’daki devre ele alınarak incelensin.
kuvvetlendiricinin giriú gerilimi VIN ile gösterilirse
Devrede
iúlemsel
V IN = V P - V N
V IN =
R2
R1
VI+
VO
R1 + R 2
R1 + R 2
VIN
R2
V 'V
R2 r O J
(3.35)
(3.36)
bulunur.
E =
R1
R1 + R 2
oldu÷u göz önüne alınırsa
R2
V I -V J
R1
=
E
V IN
1+ KV . E
(3.37)
elde edilir. Buradan hareketle
VO'
º
KV . E ª R2
« VI VO »
1 KV . E ¬ R1
¼
(3.38)
bulunur.
VI > 0 için
VO
V IN
VI < 0 için
VO
R2
§
1
R2 ¨¨1 © E .KV
elde edilir.
E.KV >> 1 için
·
r
¸¸ ¹ E .KV
VJ º
ªR
.« 2 VI E .KV »¼
¬ R1
(3.39)
LøNEER OLMAYAN UYGULAMALAR
VO
77
VJ º
ª R2
« VI E .K V »¼
¬ R1
R2
r
R2 E .K V
(3.40)
olur. Ba÷ıntıdan fark edilebilece÷i gibi, VJ eúik gerilimi ve diyodun r iç direnci
sistemin çevrim kazancı kadar küçülmektedir.
Devrenin ortalama de÷er do÷rultucusu olarak çalıúması halinde, sinüs
biçimli bir giriú iúareti için çıkıú gerilimi
VO =-
R2 V IP
R1 S
R2
r
R2 +
E . KV
ª S R1 V J
º
«¬1+ 2 R E K V »¼
2
V
IP
(3.41)
olur. Ortalama de÷er do÷rultucusu olarak kullanılmada ortaya çıkacak ba÷ıl hata
h1
S R1
VJ
2 R2 E . KV .VIP
(3.42)
úeklindedir. Yazılanlar çıkıú iúaretinin pozitif yarıperiyodu için geçerlidir.
Ba÷ıntılarda iúlemsel kuvvetlendiricinin 180o faz döndürdü÷ü ve VIP < 0 oldu÷u
dikkate alınmalıdır.
Alçak frekanslarda iúlemsel kuvvetlendiricinin açık çevrim kazancı çok
büyük de÷erlidir ve KV = KVO dur; bu nedenle h1 hatası pratikte kolayca ihmal
edilebilir. Devrenin do÷rulu÷u, sadece, iúlemsel kuvvetlendiricinin dengesizlik
gerilimine ve sürüklenmesine ba÷lı olur.
Faz döndüren do÷rultucunun frekansa ba÷ımlılı÷ı
øúlemsel kuvvetlendiricinin açık çevrim kazancının frekansa ba÷ımlılı÷ı,
faz döndüren do÷rultucunun davranıúını yüksek frekanslarda önemli oranda etkiler.
øúlemsel kuvvetlendiricinin açık çevrim kazancı
KV (jZ ) =
KVO
1+ j
Z
ZO
ENDÜSTRøYEL ELEKTRONøK
78
úeklindedir. Faz döndüren do÷rultucuda çıkıú gerilimi, iúlemsel kuvvetlendiricinin
faz döndüren giriúindeki gerilimle ve kapalı çevrim kazancının D2 diyodunun
iletimde ve kesimde olması durumlarındaki de÷eri ile belirlenir. Alçak frekanslarda
iúlemsel kuvvetlendiricinin acık çevrim kazancı çok büyük degerler aldı÷ından, faz
döndüren giriúteki gerilim çok küçüktür ve sıfır kabul edilebilir. Devrede
D2 diyodu tıkalı iken
VO
0
D2 diyodu iletimde iken
VO
R2
V
R1 I
olur.
Yüksek frekanslarda açık çevrim kazancı küçülece÷inden, iúlemsel
kuvvetlendiricinin faz döndüren giriúindeki gerilim sıfir kabul edilemez. øúlemsel
kuvvetlendiricinin giriú uçları arasındaki iúaret, devrenin giriúine sinüs biçimli bir
iúaret uygulanması durumunda, cosZt iúareti ile darbelerin toplamı biçimindedir.
Darbeler, diyodun kesime gitmesi sırasında oluúmaktadır. Sinüs biçimli iúaretin
genli÷i
V INP =
R2 Z
V IP
R1 KVO .Z O
(3.43)
V IP V J Z
KVO Z O
(3.44)
darbelerin genli÷i de
VP=2
de÷erindedir.
D2 diyodu iletimde iken devre basit bir geribeslemeli kuvvetlendirici olarak
çalıúır; ancak, çıkıú gerilimi frekansa ba÷lıdır ve frekansa ba÷lı bir hata terimi
kadar
-(R2/R1).VI de÷erinden farklı bir de÷er alır. Diyodun iletimde oldu÷u durum için
devrenin transfer fonksiyonu yazılırsa
LøNEER OLMAYAN UYGULAMALAR
79
§
·
¸§
·
1
R1
VJ
R2 ¨
¸
V O (s) = - V I ¨1¸.¨1+
R2
© R2 E KV (s)V I ¹
R1 ¨
1+
E KV (s) ¸
©
¹
R2 + r
(3.45)
R2 >> r , E.KVO >> 1 durumu için
VO =-
º
1
R 2 ª § R1 V J ·
¸
V I «1- ¨1»
R1 ¬ © R2 V I ¹ E KV (s) ¼
(3.46)
olur. øúlemsel kuvvetlendiricinin transfer fonksiyonu tek kutuplu düúme elde
edilecek úekilde kompanzasyon yapılması durumunda
KV (s) =
KVO
s
1+
ZO
úeklindedir. Bu ba÷ıntı devrenin çıkıú gerilimini veren (3.46) ba÷ıntısında yerine
konur, s yerine jZ alınır, VIP < 0 kabulü ile ZO << Z << E.KVO.Z aralı÷ında çıkıú
geriliminin genli÷i ve fazı hesaplanırsa
ª 1§
R VJ
R2
V IP «1 ¨¨1 1
VOP (Z )
R1
«¬ 2 © R2 VIP
§ R1 V J
·
¨ 1- R2 V I Z ¸
M ( Z ) = - arctan¨
¸
¨ E KVO Z O ¸
©
¹
·
¸¸
¹
2
§ Z
¨¨
© EK VO Z 0
·
¸¸
¹
2
º
»
»¼
(3.47)
(3.48)
bulunur.
D2 diyodu kesime gitti÷inde, VIN giriú gerilimindeki sıçramalar çıkıúa
yansır. Ortalama de÷er alıcıda VIN gerilimindeki distorsiyon etkili olmaz. Ancak,
giriú ve çıkıú gerilimleri arasında ek faz kaymaları oluúması durumunda, bu geçerli
de÷ildir. VIP < 0 için frekansa ba÷ımlı ba÷ıl hata
h2
olur.
2
R VJ · § Z
¸ ¨
¨¨1 1
2 © R2 VIP ¸¹ ¨© E K VO Z 0
S§
·
¸¸
¹
2
(3.49)
ENDÜSTRøYEL ELEKTRONøK
80
Yüksek frekanslı ve büyük genlikli giriú gerilimlerinde, faz döndüren
giriúte oluúan darbeler kuvvetlendiricinin aúırı sürülmesine neden olabilir. Bu
durumda iúlemsel kuvvetlendiricinin VO' çıkıú gerilimi YE yükselme e÷imi ile
de÷iúir. Bu da VO çıkıú geriliminde ek distorsiyona neden olur. Yükselme e÷iminin
çıkıú gerilimine etkisi ùekil-3.17'de verilmiútir.
VO
(R 2 /R 1 ).V IP .sinZt
(R 2/R 1).V IP .sin f
G
t
f
-2VJ
ùekil-3.17. Yükselme e÷iminin çıkıú gerilimi de÷iúimine etkisi.
Yükselme e÷imi nedeniyle ortaya çıkacak ba÷ıl hata
§V J Z G ·
1
- ¸ sinG
h3 = - (1- cosG ) - ¨
© 2YE 4 ¹
2
(3.50)
úeklindedir.G büyüklü÷ü
YE
R2 V IP
G+
sinG -2 = 0
VJ Z
R1 V J
(3.51)
denkleminin çözümünden yararlanılarak bulunabilir. G nın büyük de÷erlerinde
do÷ruluktan sapma yüksek olur. G = S/2 den itibaren çıkıú gerilimi hızlı bir düúme
gösterir.Ortalama de÷er uygulamalarında G = S/2 alınırsa, mutlak frekans
kısıtlaması
LøNEER OLMAYAN UYGULAMALAR
ZH =
S .YE
§ R2 V IP ·
2.V J .¨ 2 ¸
© R1 V J ¹
81
(3.52)
olur.ZH açısal frekansındaki hata
h3 H
§
·
1 S¨
1
1¸
- ¸
=- - ¨
2 4 ¨ R2 V IP 2 ¸
¨2 ¸
¹
© R1 V J
(3.53)
ba÷ıntısıyla verilir. Devrenin toplam hatası bu üç hatanın toplamı olur. Küçük
iúaretlerde çalıúmada, kapalı çevrim kazancının frekansa ba÷ımlılı÷ından ileri gelen
hata baskındır. Büyük iúaretlerde ise yükselme e÷iminden gelen sınırlama, h2
hatasına göre baskın duruma geçer. Yüksek frekanslı ve büyük genlikli iúaretler
iúlenecekse, kullanılacak iúlemsel kuvvetlendiricinin yükselme e÷imi büyük de÷erli
olmalı ve frekans kompanzasyonu da istenen úartlar yerine gelecek biçimde
yapılmalıdır.
Çift yollu do÷rultucu
Çift yollu do÷rultucu kurulması için yaygın olarak kullanılan devre yapısı
ùekil-3.18'da verilmiútir. Bu yapıda OP1 iúlemsel kuvvetlendiricisi ile kurulan bir
faz döndüren do÷rultucu devresi ve OP2 iúlemsel kuvvetlendiricisi ile kurulan bir
faz döndüren toplama devresi yer almaktadır. VI giriú geriliminin pozitif
de÷erlerinde V2 ve V1 gerilimleri negatif de÷erlidir. VI geriliminin negatif
de÷erlerinde ise V2 gerilimi pozitif olaca÷ından D1 diyodu tıkalıdır; bu nedenle V1
= 0 olur.
Buna göre, faz döndüren do÷rultucu devresinin V1 çıkıú gerilimi
V 1 = -V I , V I t 0
VI =0 , VI d 0
(3.54)
olmaktadır. Öte yandan, OP2 iúlemsel kuvvetlendiricisi ile kurulan faz döndüren
toplama kuvvetlendiricisinin çıkıú gerilimi
ENDÜSTRøYEL ELEKTRONøK
82
VO = -
2. R2
2. R2
VI V 1 = -( V I + 2.V 1 )
2. R2
R2
(3.55)
olur. (3.54) ba÷ıntısı (3.55) ba÷ıntısında yerine konursa, çıkıú gerilimini giriú
gerilimine ba÷layan ba÷ıntı için
2R
R
+V
1
R1
2R
2
V
2
R2
1
+
I
D1
+
OP2
+V O
V2
D2
OP1
VO
VI
ùekil-3.18. Çift yollu do÷rultucu ve geçiú karakteristi÷i.
V O = V I , VI t 0
V O = -V I , V I d 0
(3.56)
bulunur.
Böylece, çift yollu do÷rultucu iúlevi yerine getirilmiú olur. OP2 iúlemsel
kuvvetlendiricisinin çıkıúına alçak geçiren bir süzgeç ba÷lanması halinde, çıkıútan
saf bir do÷ru gerilim alınır ve bu do÷ru gerilim
VO =|V I |
(3.57)
de÷erinde olur.Bir diyottan di÷erine geçiúte ölü sürenin küçük olması için OP1
iúlemsel kuvvetlendiricisinin YE yükselme e÷iminin büyük de÷erli olması gerekir.
LøNEER OLMAYAN UYGULAMALAR
83
Etkin de÷er ölçme düzenleri
Endüstriyel elektronikte birçok devre uygulamasında bir giriú
büyüklü÷ünün (akım ya da gerilim) etkin de÷erinin ölçülmesi ve bununla da bir
düzenin kontrol edilmesi gerekli olur. Bu tür uygulamalarda etkin de÷er
çeviricilere yahut etkin de÷er ölçme düzenlerine gereksinme duyulaca÷ı açıktır.
Bir gerilimin ortalama de÷eri
|V|=
1 T
³ |V|.dt
T 0
(3.58)
ba÷ıntısıyla, etkin de÷eri ise (root mean square value: RMS)
V eff = (V 2 ) =
1 T 2
³ V .dt
T 0
(3.59)
ba÷ıntısıyla tanımlanmaktadır. Burada T ölçü süresi, gelebilecek en büyük
periyotlu giriú iúaretinin periyodundan daha büyük olacak úekilde seçilmelidir.
Böylece, ölçü süresinden ba÷ımsız bir çıkıú gerilimi elde edilir. (3.59) ba÷ıntısı
uyarınca verilen tanıma uygun olarak etkin de÷er alan düzenler gerçek etkin de÷er
çeviricileri olarak isimlendirilirler. Gerçek etkin de÷er çeviricisinin blok úeması
ùekil-3.19'da verilmiútir.
+V
I
2
V I
___
E
AGS
+V
1
E.V I
+V O =V Ieff
ùekil-3.19. Gerçek etkin de÷er çeviricisinin blok úeması.
Bu yapıda giriú iúaretinin karesi alınmakta, kare alma devresinin çıkıú gerilimi
alçak geçiren bir süzgeçten geçirildikten sonra bir karekök alma devresine
uygulanmakta, karekök alma devresinin çıkıúından da giriú geriliminin etkin
de÷erine eúit bir do÷ru gerilim alınmaktadır. Karesel ortalama için kullanılan alçak
geçiren süzgecin kesim frekansı, en düúük iúaret frekansından yeteri kadar küçük
tutulmalıdır. Bu devrenin dinami÷i dardır ve küçük giriú gerilimleri gürültüden
ayırt edilemez. Örnek vermek gerekirse, E = 10 V olan bir yapıya 10 mV'luk bir
giriú gerilimi uygulanması halinde, analog çarpma devresi çıkıúında 10 PV’luk bir
de÷iúim oluúur. Bu kadar küçük bir gerilimin ise karekök alıcının gürultüsünden
kolayca ayırt edilemeyece÷i açıktır.
ENDÜSTRøYEL ELEKTRONøK
84
Yukarıdaki sakıncayı ortadan kaldırmak üzere, dinami÷i geniúletilmiú etkin
de÷er ölçü düzeni geliútirilmiútir. Dinami÷i geniúletilmiú etkin de÷er ölçü düzeni
ùekil-3.20'de görülmektedir.
+V I
2
V
___I
VO
R
C
+
-
+V O
ùekil-3.20. Dinami÷i geniúletilmiú etkin deger ölçü düzeni.
Bu yapıda, karekök alma iúlemi yerine VO çıkıú gerilimine bölme iúlemi
gerçekleútirilmektedir. Böylece, alçak geçiren süzgeç çıkıúında
§V 2IN ·
V1 =¨
¸
©VO ¹
do÷ru gerilimi elde edilir. Sürekli halde VO = sabit oldu÷undan, devrenin çıkıú
gerilimi için
(V 2IN )
VO =
VO
V O = V 2IN = V Ieff
(3.60)
ba÷ıntısı elde edilir.
Bu yöntemin yararı, VI giriú geriliminin VI/E çarpanı ile çarpılmamasıdır.
Bu çarpan küçük giriú gerilimlerinde çok küçük de÷erler alır ; VI/E << 1 olur. Bu
devrede ise, VI giriú gerilimi VI/VO ile, baúka bir deyiúle 1'e çok yakın bir çarpanla
çarpılmakta, böylece daha büyük bir giriú gerilimi de÷iúim aralı÷ı elde
edilmektedir. VI/VO oranı düúük giriú gerilimlerinde bile yüksek do÷rulukla
sa÷lanabilmektedir.
.
LøNEER OLMAYAN UYGULAMALAR
+V
I
|V |
I
2.ln
+
-
85
Ort.
De÷er
exp
+V O
ln
ùekil-3.21. Gerçek etkin de÷er çeviricinin logaritma ve üs alma devreleri
yardımıyla gerçekleútirilmesi
Bu ilkeye dayanarak çalıúan gerçek etkin de÷er çevirici devresi, logaritma
ve ters logaritma devreleri yardımıyla gerçekleútirilebilir. Devrenin blok úeması
ùekil-3.21'de verilmiútir.
Devredeki ilk blok çift yollu bir do÷rultucudur ve giriú iúaretinin mutlak
de÷erini alır. økinci blok do÷rultulan iúaretin logaritmasını alıp 2 ile çarpar. Daha
sonraki bloklarda ise çıkıú geriliminin logaritması alınıp giriú iúaretinin
logaritmasından çıkartılmakta, elde edilen fark iúaret ters logaritmik
kuvvetlendiriciye uygulandıktan sonra alçak geçiren bir süzgeçten geçirilerek çıkıú
iúareti elde edilmektedir.
Termik ba÷laúmalı etkin de÷er çevirici
+V
RC
CC
C1
RC
+
+V
I
R1
T1
T2
R2
C2
- VEE
ùekil-3.22. Termik ba÷laúmalı etkin de÷er çevirici.
D1
+V Ieff
ENDÜSTRøYEL ELEKTRONøK
86
Etkin de÷er ölçülürken, iki direncin üzerlerinde harcanan güçlerin
karúılaútırılmasından yararlanmak da mümkündür. Bu ilkeye göre çalıúan bir devre
ùekil-3.22'de görülmektedir.
Devrede T1 tranzistoru ile R1 direnci, T2 tranzistoru ile de R2 direnci
arasında ısıl ba÷laúma oluúturulmuútur. T1 ve T2 tranzistorları bir fark
kuvvetlendiricisi oluúturacak úekilde ba÷lanmıúlardır. Uygulanan giriú gerilimi ile
R1 direnci ve bununla ısıl ba÷laúmalı olan T1 tranzistoru ısıtılmakta, sıcaklı÷ın
yükselmesiyle VBE gerilimindeki de÷iúim gözlenmektedir. Devrenin VO çıkıú
gerilimi de R2 direncine uygulanmaktadır. Fark kuvvetlendiricisinin dengesinin
sa÷lanması için R2 direncinin ve bununla ısıl ba÷laúmalı olan T2 tranzistorunun da
aynı oranda ısıtılması gerekece÷i açıktır. Bu da, ancak, VO çıkıú geriliminin giriú
iúaretinin etkin de÷erine eúit bir de÷er almasıyla mümkün olabilir. Buna göre
V O = V Ieff
olmaktadır.
Devreye bir VI giriú gerilimi uygulandı÷ında R1 - T1 kombinezonunun
sıcaklı÷ı artar. R2 - T2 kombinezonu da VO çıkıú gerilimi tarafından ısıtılır.
Bununla IC2 kolektör akımı artar. Bu artma akım IC1 akımıma eúit olana kadar sürer;
böylece bir sıcaklık geribeslemesi oluúur. Çıkıú gerilimi
I C 1 = I C 2 , V BE 1 = V BE 2
olana kadar de÷iúir.
Devreden fark edilebilece÷i gibi, iki ölçü düzeni birbirinden ısıl ve
elektriksel açıdan yalıtılmıútır. Devredeki D diyodu R2 direncinin negatif gerilimle
sürülmesini ve pozitif geribesleme oluúmasını önlemek amacıyla kullanılmaktadır.
Isıtma gücü VO2 ile orantılı oldu÷undan, sistemin çevrim kazancı da VO2 ile orantılı
olur. Bu nedenle lineer olmayan bir basamak cevabı elde edilmektedir.
LøNEER OLMAYAN UYGULAMALAR
87
3.2. øúlemsel kuvvetlendiricilerin lineer olmayan geçiú
karakteristi÷inden yararlanılarak gerçekleútirilen devreler
Gerilim karúılaútırıcılar
øúlemsel kuvvetlendiriciler kazancı yüksek ve geçiú karakteristi÷i keskin
olan, baúka bir deyiúle küçük bir giriú gerilimi de÷iúimi ile çıkıú gerilimi bir sınır
de÷erden di÷erine kadar de÷iútirilebilen devre elemanlarıdır. Bu nedenle, iúlemsel
kuvvetlendiricilerden gerilim karúılaútırıcısı olarak yararlanmak mümkündür.
øúlemsel kuvvetlendiricinin gerilim karúılaútırıcısı olarak kullanılması, ùekil3.23'de görülmektedir. Gerilim karúılaútırıcısının geçiú karakteristi÷i de ùekil3.24'de verilmiútir.
+V
+V
+V
I
+
R
+V
O
I
R
+
R
+V
+V
O
R
(a)
(b)
ùekil-3.23. øúlemsel kuvvetlendiricinin gerilim karúılaútırıcısı olarak kullanılması.
VO
V
Omaks
VR
VI
V Omin
Vomaks
2 ______
KVO
ùekil-3.24. Gerilim karúılaútırıcının geçiú karakteristi÷i.
Devrede
V P =V R , V N =V I
oldu÷u dikkate alınırsa, devrenin çıkıú gerilimi
ENDÜSTRøYEL ELEKTRONøK
88
(V R - V I ) >
V Omaks
KVO
oldu÷u sürece
V O = V Omaks
(V I - V R ) t -
V Omin
KVO
oldu÷u sürece de
V O = V Omin
de÷erini alır. Gerilim karúılaútırıcı olarak kullanılan iúlemsel kuvvetlendiricinin
geçiú e÷risi
­
V Omaks
°V Omaks , V I d V R - K
VO
VO = ®
V
Omin
° V Omin , V I t V R ¯
KVO
(3.61)
ba÷ıntısı ile karakterize edilebilir. Ba÷ıntıdan ve ùekil-3.24'den fark edilebilece÷i
gibi, devre faz döndüren bir karakteristik göstermektedir. VI giriú ve VR referans
gerilimlerinin uygulandıkları giriú uçları aksedilirse, faz döndürmeyen bir gerilim
karúılaútırıcı devresi elde edilir ve karakteristik tersine döner. Gerilim karúılaútırıcı
devresinin giriú uçları arasına gelen gerilimin büyük de÷erlere ulaúması
durumunda, iúlemsel kuvvetlendiricinin giriúine uygulanmasına izin verilen sınır
de÷erler aúılabilir ve kuvvetlendirici zarar görebilir. Bu nedenle, ùekil-3.23b'de
gösterilen biçimde, devrenin giriúine R dirençlerinden ve diyotlardan oluúan bir
koruma devresi yerleútirilir. Giriú uçları arasındaki gerilim farkı diyot iletim
eúi÷inden küçük oldu÷u sürece diyotlar tıkalıdır. Devrenin giriúinden içeriye do÷ru
bakıldı÷ında 2R direnci ve buna seri gelen iúlemsel kuvvetlendirici giriú direncinin
toplamı görülece÷inden, giriú direnci çok büyük de÷erli, pratik olarak sonsuz olur.
Giriú uçları arasındaki fark diyot iletim yönü gerilimini aútı÷ında, uygulanan
gerilimin yönüne ba÷lı olarak diyotlardan biri iletime geçer ve iúlemsel
LøNEER OLMAYAN UYGULAMALAR
89
kuvvetlendiricinin iki giriú ucu arasındaki gerilim, bir diyot gerilimine kenetlenmiú
olur; dolayısıyla sınır de÷erin aúılması önlenir. Ancak, bu durumda toplam giriú
direnci yaklaúık olarak 2R de÷erindedir ve bunun da sürücü devreyi yükleyece÷i
dikkate alınmalıdır.
øúlemsel kuvvetlendiricinin konum de÷iútirme eúi÷i, baúka bir deyiúle
karakteristi÷in sıfır geçiú noktası VI = VR den farklı olur ve ECV bir hata terimi
olmak üzere
ª
1 º
V I = V R «1¬ E CV »¼
(3.62)
de÷erini alır. Bu farklılık, iúlemsel kuvvetlendiricinin ortak iúareti zayıflatma
oranının (CMRR) sonsuz olmamasından kaynaklanır. Bu hata, de÷iúik bir devre
kurulmasıyla kolayca elimine edilebilir; devre yapısı ve bunun geçiú karakteristi÷i
ùekil-3.25'de verilmiútir.
VO
VOmaks
R
+V I
VR
-V R
R
+
R/2
VI
+VO
VOmin
Vomaks
4 ______
K VO
ùekil-3.25.Geçiú hatası azaltılmıú gerilim karúılaútırıcı ve geçiú karakteristi÷i.
Bu devrede iúlemsel kuvvetlendiricinin faz döndürmeyen giriúi bir R/2 direnci
üzerinden toprak potansiyelinde tutulmakta, negatif de÷erli referans gerilimi ile
giriú gerilimi ise birer R direnci üzerinden iúlemsel kuvvetlendiricinin faz döndüren
giriúine uygulanmaktadır. Devredeki R dirençleri ile bir toplama devresi
oluúturulmuútur. Devrenin her iki giriúine ba÷lanan dirençlerin de÷erce eúit
olmaları, iúlemsel kuvvetlendiricinin dengeli çalıúması için bir zorunluluktur. Bu
nedenle, faz döndürmeyen giriúe ba÷lanan direnç R/2 de÷erinde seçilmiútir. Giriú
geriliminin referans gerilimine eúit iken karakteristi÷in sıfırdan geçmesi için
referans geriliminin Vref = -VR biçiminde negatif de÷erli olması gerekece÷i açıktır.
ENDÜSTRøYEL ELEKTRONøK
90
Konum de÷iútirme gerilimini etkileyen di÷er faktörler, iúlemsel
kuvvetlendiricinin giriú gerilim ve akım dengesizlikleri ile sürüklenmesi
olmaktadır. Kuvvetlendiricinin faz döndüren giriúi ile toprak ucu arasına gelen
toplam direnç RN ile, faz döndürmeyen giriúine gelen toplam direnç de RP ile
gösterilsin. Bu durumda devrenin giriú dengesizlik gerilimi
ª
ª
I IO º
I º
+ R N . « I I - IO » - V IO
V I cO= - R P . « I I +
»
2 ¼
2 ¼
¬
¬
(3.63)
ve bunun sıcaklıkla sürüklenmesi de
ª ' I I 1 ' I IO º
ª ' I I 1 ' I IO º ' V IO
' V IO
= - R P .«
+
+ R N .«
+
»
¬ 'T 2 'T ¼
¬ 'T 2 'T »¼ 'T
'T
(3.64)
olur. Bu hata, dengesizlik gerilimi küçük kuvvetlendirici kullanılarak ve RP = RN
alınarak azaltılabilir.
Buraya kadar ele alınan etkenler, yavaú de÷iúen giriú iúaretleri için
geçerlidir. Hızlı de÷iúen iúaretlerde hem giriú iúaretinin hem de iúlemsel
kuvvetlendiricinin yükselme e÷imi iúin içine girer. Giriú iúaretinin yükselme e÷imi
k olsun. Devrenin karúılaútırma sınırları
VR
V
V Omaks
, V R Omin
K VO
K VO
úeklindedir. øúlemsel kuvvetlendiricinin band geniúli÷inin sonsuz olması ve
yükselme e÷iminin sadece giriú iúaretinin yükselme e÷iminden kaynaklanması
durumunda VO çıkıú iúaretinin yükselme e÷imi k.KVO olur. Giriú iúaretinde hızlı
de÷iúimler söz konusu oldu÷unda, çıkıú gerilimi kuvvetlendiricinin geçici hal
cevabına da ba÷lıdır. VO çıkıú geriliminin zamana ba÷ımlılı÷ı giriú iúaretinin
yükselme e÷iminin, kuvvetlendiricinin ts toparlanma süresinin, fo band geniúli÷inin
ve YE yükselme e÷iminin bir fonksiyonudur.
LøNEER OLMAYAN UYGULAMALAR
VI
VI'
k.t
k.t '
V2'
V2
V1
V1'
VR
VO
91
ts
t0
t1
t1'
t2
t2'
t'
t
VOmaks
t
VOmin
ùekil-3.26. Gerilim karúılaútırıcının zaman diyagramı.
Giriú iúaretinin zamanla lineer olarak de÷iúti÷i ve bu de÷iúimin hızının k
oldu÷u kabul edilsin. Bu duruma iliúkin de÷iúimler ùekil-3.26'da verilmiútir. t = t0
da karúılaútırıcının konum de÷iútirmesi gerekirdi. Ancak, úekilden de izlenebilece÷i
gibi, karúılaútırıcı t0 da de÷il, fakat t1 anında konum de÷iútirmekte, t = t2 anında da
VO çıkıú gerilimi son de÷erine ulaúmaktadır. Fark edilebilece÷i gibi,
karúılaútırıcının konum de÷iútirmeye baúlaması için geçen süre
t s = t1 - t0
farkına eúittir. t2 büyüklü÷ü kuvvetlendiricinin fo kesim frekansına ve YE yükselme
e÷imine ba÷lıdır. Giriú geriliminin t2 anında alaca÷ı de÷eri hesaplayalım. t1 anında
iúlemsel kuvvetlendirici doymadan çıkar ve lineer bölgeye girer. Bu bölgede
transfer fonksiyonu
KV (s) =
KVO
s
1+
Zo
úeklindedir. øúlemsel kuvvetlendiricinin geçiú bölgesindeki davranıúı için ùekil3.27'deki eúde÷er devreden yararlanılabilir. Bu bölgede iúlemsel kuvvetlendirici
lineer çalıúma bölgesindedir.
ENDÜSTRøYEL ELEKTRONøK
92
Ro
+V I
+V R
+V I
+
+VO
V IN = V I - V R
+V R
+
KV V IN
-
+V O
Co
ùekil-3.27. Lineer çalıúma bölgesinde iúlemsel kuvvetlendiricinin eúde÷er devresi.
Ancak, lineer çalıúma bölgesine girene kadar kuvvetlendirici doymada çalıúır.
øúlemsel kuvvetlendiricinin doymadan çıkıp lineer bölgeye girdi÷i andan itibaren
geçen zaman t' ile gösterilsin. Devrenin zaman domenindeki davranıúı, bir
transformasyon yardımıyla VI - t düzleminden VI' - t' düzlemine geçilerek
incelenebilir.
VI' - t' düzleminde VI' giriú gerilimi
V I c = k.t c+V 1c
(3.65)
úeklinde yazılabilir. Bu durumda s domeninde çıkıú gerilimi yazılırsa
V O (s) = -
Z O ª k. KVO KVO .V 1 c V Omaks º
+
s
Z O + s «¬ s2
Z O »¼
(3.66)
elde edilir. Bu ba÷ıntıdan hareketle vo(t') zaman domeni cevabı hesaplanırsa
º
ª k
- V 1c ».(1 - exp- Z O .t c )
v o ( t c ) = - KVO .k.t c + KVO .«
¼
¬Z O
+ V Omaks .exp(- Z O .t c )
(3.67)
bulunur. ZO.t' << 1 oldu÷u sürece üstel terimler yerine bunların seri açılımları
alınabilir. Böylece
ª k V Omaks
º Z 2O . t c2
-V 1 c ».
v o ( t c ) = - KVO .« ¬ Z O KVO
¼ 2
-( KVO .V 1 c +V Omaks ).Z O . t c +V Omaks
(3.68)
LøNEER OLMAYAN UYGULAMALAR
93
elde edilir. t' = t2' anında çıkıú gerilimi iúlemsel kuvvetlendiricinin VOmin negatif
doyma gerilimine ulaúır. Karúılaútırma iúleminin sınırındaki giriú gerilimi de÷eri V2'
ile gösterilmiútir. Bu büyüklük, k nın büyük de÷erlerinde önemli ölçüde yüksek
de÷erler alabilir. Hızlı de÷iúen giriú gerilimlerinde
º
ªV Omaks
>> «
+V 1 c »
¬ KVO
¼
ZO
k
c
KVO .V 1 = KVO .k.t s >> V Omaks
olmak üzere
t 2 c = - t s + t 2s + 2.
V Omaks - V Omin
KVO .Z O .k
(3.69)
elde edilir. t2 anındaki V2 giriú gerilimi orijinal koordinat sisteminde yazılırsa
V 2 = V R + k.( t s + t 2 c)
V 2 = V R + k 2 . t 2s + 2.k
V Omaks - V Omin
KVO .Z O
(3.70)
bulunur. Hızlı de÷iúen giriú gerilimleri için devrenin çıkıú gerilimi
­V Omaks
°
VO = ®
°̄V Omin
V I d V R + k.t s
V I t V R + k 2 t 2s + 2k
V Omaks - V Omin
KVO .Z O
(3.71)
de÷erini alır. Çok büyük k de÷erlerinde iúlemsel kuvvetlendiricinin YE yükselme
e÷imi t2 süresini belirleyen temel faktör olur. Bu durumda t2' büyüklü÷ü t2'' gibi bir
de÷er alır ve bu büyüklük
t 2 cc =
V Omaks - V Omin
YE
(3.72)
ba÷ıntısıyla hesaplanabilir. (3.69) ba÷ıntısıyla verilen süre t2' ile gösterilirse, t2'' >>
t2' olaca÷ı açıktır. Baúka bir deyiúle, iúlemsel kuvvetlendiricinin
YE
e÷imisınırlayıcı bir etken olmaktadır. (3.72) ba÷ıntısı çıkıú gerilimini veren
ba÷ıntıya götürülürse
ENDÜSTRøYEL ELEKTRONøK
94
V I d V R + k . ts
­V Omaks
°
=
VO ®
°̄V Omin
V I t V R + k. t s + k
(3.73)
V Omaks - V Omin
YE
bulunur. Bu durumda, VO çıkıú geriliminin yükselme e÷imi, VI giriú geriliminin
yükselme e÷iminden ba÷ımsız olarak iúlemsel kuvvetlendiricinin YE yükselme
e÷imi ile belirlenir.
V
D
+V I
+V R
Z
VO
+V
D
VR
D
V
R
+
R
+V O
4
V O
R/2
V
R
+V
-V
I
- (V +V )
Z D
V Z +V
_______
D
K
VO
Z
D
VR
I
R
R
+
R/2
+V O
VI
-V D
2
V Z +V D
_______
K
VO
ùekil-3.28. Diyot-Zener kombinezonları üzerinden geribeslemeli karúılaútırıcı yapıları.
Ele alınan devrede çıkıú gerilimi, iúlemsel kuvvetlendiricinin pozitif ve
negatif yönlerdeki dalgalanma sınırları ile sınırlanmaktadır. Devrenin çıkıúından
belli seviyeler arasında de÷iúen iúaretler elde edilmesi istenirse, diyot-Zener diyodu
kombinezonları üzerinden iúlemsel kuvvetlendiriciye geribesleme uygulanarak
çıkıú iúaretinin sınırlanması yoluna gidilir. Diyot-Zener diyodu kombinezonları
üzerinden geribesleme uygulanmıú iki devre yapısı ve bunların geçiú e÷rileri ùekil3.28'de verilmiútir. ùekil-3.28'deki devreler geribeslemeli yapılar olduklarından
bunlarda ts toparlanma süresi elimine edilmiútir. Ancak, geribesleme nedeniyle
kararsızlık sorunu ortaya çıkaca÷ından, frekans kompanzasyonu gerekli olur ki, bu
da çalıúma hızını sınırlar.
ùekil-3.28a'daki devrede geribesleme yolu üzerinde sırt sırta ba÷lanmıú iki
Zener diyodu yer almaktadır. Bununla, devrenin çıkıú gerilimi her iki yönde de VZ
+ VD de÷eriyle, baúka bir deyiúle bir diyot iletim yönü gerilimi ile bir Zener
geriliminin toplamı ile sınırlanmaktadır.
LøNEER OLMAYAN UYGULAMALAR
95
ùekil-3.28b'deki devrede ise çıkıú gerilimi pozitif yönde VZ zener gerilimi,
negatif yönde de VD diyot gerilimi arasında de÷iúmektedir.
VR = 0 alınması durumunda, buraya kadar incelenen karúılaútırıcı
devrelerinin sıfır geçiú karúılaútırıcısına dönüúece÷i açıktır.
D
C
+V I
D
VZ + VD
+
+V
O
ùekil-3.29. Tepe de÷er karúılaútırıcısı.
VI
VIP
t
VO
+(VZ+VD)
t
-(VZ+VD)
ùekil-3.30. Tepe deger karúılaútırıcısının giriú ve çıkıú iúaretlerinin zamana göre de÷iúimleri.
Geribeslemeli sıfır geçiú karúılaútırıcıları, basit bir de÷iúiklik yapılarak tepe
de÷er karúılaútırıcısına dönüútürülebilir. Böyle bir devre ùekil-3.29'da, bunun giriú
ve çıkıú iúaretlerinin de÷iúimi de ùekil-3.30'da verilmiútir. Giriúe seri ba÷lanan
elemanın empedansı Z = 1/sC úeklindedir ve bu C elemanı kuvvetlendirici ile
birlikte bir türev alıcı oluúturur. Giriú akımı tepelerde sıfır olaca÷ından devre
tepeye ulaúıldı÷ında konum de÷iútirir.
ENDÜSTRøYEL ELEKTRONøK
96
Schmitt tetikleme devreleri
Bir önceki kısımda incelenen basit gerilim karúılaútırıcılarında giriú ve
çıkıú gerilimleri arasında do÷rudan do÷ruya ba÷ımlılık vardır. Yavaú de÷iúen giriú
iúaretlerinde, cıkıú iúareti de yavaú de÷iúen bir iúaret olur. Bunun yanısıra, giriú
iúaretindeki olası bir gürültü, konum de÷iútirmeyi kararsız hale getirebilir. Bu
nedenle, bazı uygulamalarda histerezisli bir geçiú karakteristi÷i gösteren yapılar
daha elveriúli olabilir. Geçiú karakteristi÷i histerezis gösteren gerilim
karúılaútırıcıları Schmitt tetikleme devreleri olarak isimlendirilirler. Schmitt
tetikleme devreleri pozitif geribeslemeli düzenlerdir. Bir Schmitt tetikleme
devresinin geçiú e÷risi faz döndüren karakteristik gösterebilece÷i gibi faz
döndürmeyen nitelikte de olabilir. øúlemsel kuvvetlendirici ile gerçekleútirilen ve
faz döndüren karakteristik gösteren bir Schmitt tetikleme devresi ùekil-3.31'de
verilmiútir. Devrenin geçiú e÷risi de úekil üzerinde gösterilmiútir. Pozitif
geribesleme devreyi çok hızlı kılar. Devrenin anahtarlama hızı iúlemsel
kuvvetlendiricinin YE yükselme e÷imi ile belirlenir. Devrenin geçis
karakteristi÷ini veren ba÷ıntılar
­
°V Omaks
°
VO = ®
° V Omin
°¯
·
V Omin § R1 + R2
R2
- R1 ¸¸
¨¨
VR R1 + R2
R1 + R2 © K VO
¹
+
§
·
V Omaks R1 R2
R2
- R1 ¸¸
¨¨
V It
VRR1 + R2
R1 + R2 © K VO
¹
VI d
(3.74)
olur. VOmaks = - VOmin olması hali için devrenin histerezis karakteristi÷inin geniúli÷i
+V
I
+V R
R 1 // R 2
+
R1
R2
+V O
VO
V Omaks
VI
C
2
V Omin
VH
ùekil-3.31. Faz döndüren Schmitt tetikleme devresi ve geçiú karakteristi÷i.
LøNEER OLMAYAN UYGULAMALAR
VH =2
97
R1
V Omaks
R1 + R 2
(3.75)
olur. VH histerezis geniúli÷i R2 direncinin de÷eri arttırılarak azaltılabilir. Ancak,
devrenin çevrim kazancı için KVO R1/(R1+R2) > 1 úartının yerine gelmesi gerekir.
Büyük R2 de÷erlerinde, kuvvetlendiricinin fark iúaret giriú kapasitesi devrenin
anahtarlama hızını etkiler. Bu etkiyi ortadan kaldırabilmek üzere R2 direncine
paralel bir C2 kondansatörü ba÷lanır. Bu kondansatörün kapasitesi
C 2 !!
R1
C id
R2
olacak úekilde seçilmelidir.
VI ve VR gerilimlerinin yerlerinin de÷iútirilmesi halinde faz döndürmeyen bir
Schmitt tetikleme devresi elde edilir. Faz döndürmeyen Schmitt tetikleme devresi
ùekil-3.32'de görülmektedir.
+V R R
1 // R2
+V I
V O
V Omaks
+
+V O
R2
R1
VI
V
C2
Omin
VH
ùekil-3.32. Faz döndürmeyen Schmitt tetikleme devresi.
Bu devre için çıkıú gerilimini giriú gerilimine ba÷layan ba÷ıntı
­
°V Omaks
°
VO = ®
° V Omin
°¯
R1 + R2 + V Omin § R1 + R2 - ·
¨¨
VI t
VR
R1 ¸¸
R2
R2 © K VO
¹
+
§
·
R+ R2 + V Omaks R1 R2 ¨¨
VI d
VR
R1 ¸¸
R2
R2 © K VO
¹
olur. VOmaks = - VOmin için devrenin histerezis geniúli÷i
(3.76)
ENDÜSTRøYEL ELEKTRONøK
98
VH =2
R1
V Omaks
R2
(3.77)
olur
Buraya kadar ele alınan iki yapıda da çıkıú gerilimi ve histerezis geniúli÷i
besleme gerilimine ba÷ımlıdır. Bazı devre uygulamaları açısından sakıncalı
olabilecek bu ba÷ımlılık, devrenin çıkıú geriliminin maksimum de÷eri stabilize
edilerek ortadan kaldırılabilir. Bunun için genellikle Zener diyotlarından
yararlanılmaktadır. Çıkıú geriliminin Zener diyodu ile stabilize edilmesi ile bu
durumda elde edilen giriú - çıkıú geçiú karakteristi÷i ùekil-3.33'de gösterilmiútir.
Devrede iúlemsel kuvvetlendiricinin çıkıúına ba÷lanan RS direnci, Zener diyodunun
ve iúlemsel kuvvetlendiricinin çıkıú akımını sınırlar. Geribesleme direnci seri
direncin di÷er ucuna ba÷lanmakta ve çıkıú da bu uçtan alınmaktadir. Çıkıú
dü÷ümüne ba÷lanan sırt sırta iki Zener diyodu yardımıyla VO gerilimi her iki yönde
de VZ + VD de÷eriyle sınırlanmaktadır.
+V I
R 1 //R 2
RS
+
+V R
+V O
R2
R1
D1
D2
ùekil-3.33. Çıkıú geriliminin Zener diyodu ile stabilize edilmesi.
+V I
R 1 / /R2
R
+
+V R
R1
S
+V O
R 2
D
ùekil-3.34. Asimetrik çıkıú gerilimi veren Schmitt tetikleme devresi .
LøNEER OLMAYAN UYGULAMALAR
99
Bu bölümde incelenen devrelerde gerek karúılaútırma sınırları, gerekse
çıkıú geriliminin de÷iúim aralı÷ı simetrik olur. Ancak, simetrik karúılaútırma ve
çıkıú gerilimleri, tek kaynaktan beslenen dijital devre uygulamalarına uygun
de÷ildir. Bunun için çıkıú geriliminin de÷iúim aralı÷ı ve karúılaútırma sınırları
asimetrik olan devreler geliútirilmiútir. Çıkıú gerilimi asimetrik olacak úekilde
düzenlenmiú bir Schmitt tetikleme devresi ùekil-3.34'de görülmektedir. Bu
devrede, çıkıúta tek bir Zener diyodu yer almaktadır. Pozitif çıkıú gerilimlerinde bu
eleman Zener diyodu olarak çalıúır ve devrenin çıkıú gerilimini +VZ de÷erinde
sınırlar. negatif çıkıú gerilimlerinde ise eleman iletim yönünde kutuplanaca÷ından,
çıkıú gerilimi VD iletim yönü gerilimi ile sınırlanır. Böyle bir yapıda VR referans
gerilimi için uygun bir de÷er
VR=
·
V Z - V D § R1 + R 2
- R1 ¸
.¨
¹
2. R2 © KVO
VR|
1 R1
(V D - V Z )
2 R2
(3.78)
olur. Böylece sıfır karúılaútırıcısı olarak çalıúan bir devre elde edilir.
Pencere karúılaútırıcılar
Basit karúılaútırıcılar VI giriú geriliminin bir VR referans geriliminden
büyük yahut küçük oldu÷unu belirleyen devre yapılarıdır. Bazı uygulamalarda ise
VI giriú geriliminin belirli bir gerilim aralı÷ı içerisine düúüp düúmedi÷inin
belirlenmesi istenir. Bu karúılaútırma iúlevini yerine getiren karúılaútırıcılar
pencere karúılaútırıcılar olarak isimlendirilirler. Baúka bir deyiúle, pencere
karúılaútırıcılar VI giriú geriliminin VR- ve VR+ aralı÷ında bulunup bulunmadı÷ını
belirlerler. Pencere karúılaútırıcı, iki basit karúılaútırıcı devresinin diyotlu bir kapı
ile biraraya getirilmesiyle kolayca oluúturulabilir. Devre yapısı ùekil-3.35'de
verilmiútir.
ENDÜSTRøYEL ELEKTRONøK
100
+V
CC
R
+
+V
R
V O1
+
K1
D1
+V
O
+V I
+V
VO2
D2
+
-
R
K
2
ùekil-3.35. Pencere karúılaútırıcı.
Yapıda K1 faz döndüren bir karúılaútırıcıdır ve tanım ba÷ıntıları
V I > V +R iç in V O1 = V Omin
V I < V +R iç in V O1 = V Omaks
úeklindedir. K2 ise faz döndürmeyen bir karúılaútırıcıdır ve bunun tanım ba÷ıntıları
da
V I > V -R iç in V O 2 = V Omaks
V I < V -R iç in V O 2 = V Omin
biçimindedir. Buna göre
V I < V -R ,V +R iç in
V O 2 = V Omin , D2 iletimde
V O1 = V Omaks , D1 kesimde
olur. Diyotlu VE kapısı çıkıúında VO = VOmin elde edilir.
V -R < V I < V +R iç in
V O 2 = V Omaks , D2 kesimde
V O1 = V Omaks , D1 kesimde
olaca÷ından, kapı çıkıúında VOmaks seviyesi olur.
+
V I > V R ,V R iç in
V O 2 = V Omaks ,
D1 kesimde
V O1 = V Omin , D1 iletimde
LøNEER OLMAYAN UYGULAMALAR
101
olaca÷ından, devrenin çıkıú gerilimi VO = VOmin seviyesini alır. Fark edilebilece÷i
gibi, giriú geriliminin VR- - VR+ aralı÷ında bulunması halinde çıkıú gerilimi VOmaks
de÷erini, bu aralı÷ın dıúındaki giriú gerilimi de÷erleri için de VOmin de÷erini
almaktadır.
Fonksiyon üreteçleri
Bir çok devre uygulamasında kare dalga, üçgen dalga, sinüs, darbe gibi
çeúitli türden dalga úekillerinin oluúturulmasına sıkça gereksinme duyulur. Bu tür
dalga úekillerinin üretilmesi açısından, özellikle alçak frekanslarda, ideal birer
eleman gibi davranan iúlemsel kuvvetlendiricilerle kurulan fonksiyon üreteci
yapıları iyi bir çözüm oluútururlar. Alçak frekanslarda elde edilen yüksek
do÷rulu÷a karúılık, çalıúma frekansı yükseldikçe, daha önceki bölümlerde ele
alınan hata kaynakları da etkili olmaya baúlayacaklarından, üretilen dalga
úekillerinde bozulmalar ortaya çıkar.
Ilkesel olarak, iúlemsel kuvvetlendiriciler yardımıyla oluúturulan fonksiyon
üreteci ùekil-3.36'da verilen bloklardan oluúur. ùekil-3.36'dan fark edilebilece÷i
gibi, devre bir analog anahtardan, bir integral alıcıdan, bir Schmitt tetikleme
devresinden ve bir de üçgen/sinüs çeviriciden oluúmaktadır. Bu tür devrelerde
üretilen temel dalga úekilleri kare dalga ve üçgen dalgadır. Sinüs biçimli iúaretler
ise, üçgen dalganın bir dalga úekillendiriciden geçirilmesi ile elde edilir. Baúka bir
deyiúle, ilk önce dolup-boúalmalı osilatör ilkesine göre çalıúan düzenler yardımıyla
üretilmesi daha kolay olan dalga úekilleri elde edilmekte, sinüs dalga úekli ise bir
dalga úekillendiricisi yardımıyla üretilmektedir. ùekil-3.36'da blok úeması verilen
dolup-boúalmalı osilatör yapısının iúlemsel kuvvetlendiriciler yardımıyla ne úekilde
gerçekleútirilece÷i ùekil-3.37'de gösterilmiútir.
ANALOG
ANAHTAR
øNTEGRAL
ALICI
SCHMITT
TETøKLEME DEVRESø
KARE
O
ÜÇGEN
O
SøNÜS
ÇEVøRÝCø
ùekil-3.36. Fonksiyon üretecinin blok úeması.
SøNÜS
O
ENDÜSTRøYEL ELEKTRONøK
102
C1
+V O1
R 3 //R 4
R1
+
+
R3
R2 = R 1
R
+VO2
4
ùekil-3.37. Iúlemsel kuvvetlendiricilerle gerçekleútirilen dolup-boúalmalı osilatör yapısı.
ùekilden fark edilebilece÷i gibi, devre bir integral alıcı ve bir de Schmitt tetikleme
devresi içermektedir. Integral alıcı çıkıúından rampa yahut üçgen dalga biçiminde
bir çıkıú iúareti, Schmitt tetikleme devresi çıkıúından ise darbe yahut kare dalga
biçiminde bir çıkıú iúareti alınmaktadır.
R3
V Omaks
R4
R3
+
V K = - V Omin
R4
-
VK =-
(3.79)
(3.80)
Devredeki integratörün zaman sabiti W = R1.C1 de÷eriyle belirlenmiútir.
Schmitt tetikleme devresinin konum de÷iútirme eúikleri ise
ba÷ıntıları ile verilir. Bunlar biraraya getirilirse,üretilecek iúaretin periyodu
T = T 1 + T 2 = R1 C 1
R 3 ªV Omaks - V Omin V Omin - V Omaks º
«
»
R 4 ¬ V Omaks
V Omin
¼
(3.81)
olur. Kullanılan iúlemsel kuvvetlendiriciler için VOmaks = -VOmin ise, iúaretin
periyodu ve frekansı
T = 4 R1 C 1
f =
1
T
R3
R4
(3.82)
(3.83)
LøNEER OLMAYAN UYGULAMALAR
103
ba÷ıntıları ile hesaplanabilir. Yapıda, C1 kondansatörü aynı R1 direnci üzerinden
doldurulup boúaltıldı÷ından, üçgen ve kare dalga, baúka bir deyiúle simetrik
iúaretler üretilmektedir. Elde edilecek dalga úekilleri ùekil-3.38'de verilmiútir. Fark
edilebilece÷i gibi, kare dalga iúlemsel kuvvetlendiricinin çıkıú geriliminin iki
yöndeki sınır de÷erleri arasında, üçgen dalga ise Schmitt tetikleme devresinin
konum de÷iútirme eúik gerilimleri arasında de÷iúmektedir.
+VO1
+
VK
t
VK
+V 02
VOmaks
t
Vomin
ùekil-3.38. Üretilen dalga úekilleri.
R
D
1
R1
R1
D2
C1
a
Rb
+V O1
R 3 //R 4
P1
+
D P1
R2
+
R3
R4
+V O2
ùekil-3.39. Darbe-periyot oranı de÷iútirilebilen fonksiyon üreteci.
Bazı uygulamalarda, darbe-periyot oranı farklı olan iúaretlerle çalıúılması
gerekebilir. Bu tür uygulamalar için yukarıda anlatılandan farklı bir fonksiyon
üreteci devresinin gerekli olaca÷ı açıktır. Devre üzerinde bir de÷iúiklik yapılarak
C1 kondansatörünün farklı yollardan doldurulup boúaltılması mümkündür. Böylece,
darbe-periyot oranı farklı de÷erler alabilen iúaret üreteci düzenleri kolaylıkla
gerçekleútirilebilir. Kondansatörün farklı yollardan doldurulup-boúaltıldı÷ı bir
devre yapısı ùekil-3.39'da verilmiútir. Bu devrede R1 direnci iki kola ayrılmıútır.
Kondansatör kollardan biri üzerinden dolmakta, di÷eri üzerinden de boúalmaktadır.
Bu iúlem, kollar üzerine yerleútirilen D1 ve D2 diyotları yardımıyla sa÷lanmaktadır.
ENDÜSTRøYEL ELEKTRONøK
104
P1 potansiyometresi yardımıyla kollardan birindeki seri direnç de÷eri arttırılırken,
di÷er koldaki direnç de÷eri ise azaltılmaktadır. Böylece, potansiyometrenin
konumuna ba÷lı olarak, kolların direnci ve bununla da kondansatörü doldurupboúaltan akımlar de÷iútirilmiú olur. Bu durumda darbe-periyot oranı
Ra
T1
=
T 1 + T 2 R a + Rb
olur. Devreden hareket edilirse
Ra =R1 '+ P1 (1 - D )
R b =R1 '+D P1
(3.84)
(3.85)
bulunur. Böylece, iúaret frekansı
f =
1 R4
1
=
T R 3 2( R a + Rb ) C1
(3.86)
olur. Fark edilebilece÷i gibi, darbe-periyot oranının potansiyometrenin D konum
çarpanına ba÷lı olmasına karúılık, f frekansı bu çarpandan ba÷ımsız kalmaktadır.
Dolayısıyla, frekansı sabit tutarak darbe-periyot oranını de÷iútirmenin mümkün
olaca÷ı açıktır.
Frekansı ayarlanabilir osilatörler
Buraya kadar incelenen yapılarda, elemanların belli de÷erleri için elde
edilecek osilasyonun frekansının sabit kalaca÷ı kolayca gösterilebilir. Oysa, bir çok
uygulamada frekansı gerilimle kontrol edilebilen fonksiyon üreteçlerine
gereksinme duyulmaktadır. Iúlemsel kuvvetlendiriciler yardımıyla gerilim
kontrollu osilatör yapıları kolayca gerçekleútirilebilir. Böyle bir gerilim kontrollu
iúaret üreteci devresi ùekil-3.40'da görülmektedir.
LøNEER OLMAYAN UYGULAMALAR
105
R4
+
+V I
R3
V1
T1
R3
+
R
T2
V2
C
+
R1
+V O1
üçgen
R2
+
-
+V O2
kare
ùekil-3.40. Iúlemsel kuvvetlendiricilerle kurulan gerilim kontrollu osilatör devresi.
Devrede frekans kontrolu, VI ve -VI gerilimlerinin de÷iútirilmesiyle
sa÷lanır. Bu gerilimler, giriúe uygulanan pozitif kontrol geriliminden OP1 ve OP2
iúlemsel kuvvetlendiricileri yardımıyla türetilirler. OP1 iúlemsel kuvvetlendiricisi
faz döndürmeyen birim kazançlı bir kuvvetlendirici olarak, OP2 iúlemsel
kuvvetlendiricisi ise yine birim kazançlı ve faz döndüren bir kuvvetlendirici olarak
görev yapar.
OP1 ve OP2 iúlemsel kuvvetlendiricilerinin çıkıúlarından alçak empedanslı
olarak alınan VI ve -VI gerilimleri, çıkıú geriliminin yönüne ba÷lı olarak T1 ve T2
anahtar tranzistorları üzerinden integral alıcının giriúine uygulanır. Anahtar
tranzistorlarının uçlarındaki gerilim düúümü mV'lar mertebesindedir ve rahatlıkla
ihmal edilebilir. Schmitt tetikleme devresinin histerezis aralı÷ı üçgen dalganın
genli÷ini belirler. Iúlemsel kuvvetlendiricinin çıkıú geriliminin de÷iúim sınırlarının
simetrik oldu÷u kabul edilirse, Schmitt tetikleme devresinin histerezis aralı÷ı
VH =2
R1
V Omaks
R2
(3.87)
olaca÷ından, üçgen dalganın genli÷i de bunun yarı de÷erini alır ve
V DM =
R1
V Omaks
R2
(3.88)
olur. Devrenin osilasyon frekansı ile giriú kontrol gerilimi arasındaki iliúki ise
f =
VI
R2
4R.C.V Omaks R1
(3.89)
ENDÜSTRøYEL ELEKTRONøK
106
ba÷ıntısıyla ifade edilebilir. Ba÷ıntıdan fark edilebilece÷i gibi, osilasyon frekansı
giriú gerilimiyle do÷ru orantılıdır. Bu nedenle, devre gerilim-frekans çevirici olarak
kullanılmaya elveriúlidir.
Darbe-boúluk oranı ayarlanabilir fonksiyon üreteci
ùekil-3.41. ùekil-3.40'deki devreyi darbe-boúluk oranı de÷iútirilebilen bir osilatör devresine
dönüútürmek üzere kullanılan ek devre.
Buraya kadar ele alınan fonksiyon üreteci devreleri, aynı anda kare dalga
ve üçgen dalga üreten devre yapılarıdır. Bazı uygulamalarda ise darbe-periyot oranı
de÷iútirilebilen dalga úekillerine gereksinme duyulur. Bunun için bir önceki
devrede basit bir de÷iúiklik yapılarak çözüme gidilebilir. ùekil-3.40'daki devreyi
darbe-boúluk oranı de÷iútirilebilen bir fonksiyon üretecine dönüútürmek üzere
yapılacak ekler ùekil-3.41'de verilmiútir. Burada, önceki devredeki V1 ve V2
gerilimleri daha farklı yapılır ve bu gerilimler ùekil-3.41'deki devre ile
oluúturulurlar; bu devre yardımıyla testere diúinin yükselen ve düúen kenarlarına
farklı de÷erler verilmektedir. Buna göre
T1 =
2.R.C.V Omaks R1
R2
V1
(3.90)
T2 =
2. R.C.V Omaks R1
|V 2 |
R2
(3.91)
olur. Buradan hareket edilirse, çıkıú iúaretinin periyodu için
LøNEER OLMAYAN UYGULAMALAR
107
§ 1
1 · R1
T = T 1 + T 2 = 2.R.C.¨ +
¸
V Omaks
© V 1 |V 2 |¹ R2
(3.92)
elde edilir. Ilgili büyüklükler bu ba÷ıntıda yerlerine konursa
1
V1
+
1
|V 2 |
1
1
.[ R3 + (1 - D ). R4 + R3 + D . R4 ] =
[2. R3 + R4 ]
V I . R3
V I . R3
elde edilir. Görülebilece÷i gibi, periyot D konumundan ba÷ımsız olmaktadır.
Böylece, çıkıú iúaretinin frekansı için
f =
R3
V I R2
2.R.C.[2. R3 + R 4 ] V Omaks R1
(3.93)
ba÷ıntısı bulunur. T1/T ve T2/T oranları, R4 potansiyometresi yardımıyla
R3
2. R 3 + R4
ve
R3 + R4
2. R 3 + R 4
de÷erleri arasında ayarlanabilir.
Aynı anda 90o faz farklı üçgen ve karedalga iúaretleri üreten üreteçler
Buraya kadar ele alınan devrelerden fark edilebilece÷i gibi, fonksiyon
üreteçlerinde genlik stabilizasyonu problemsiz olarak Schmitt tetikleme devresinin
histerezis aralı÷ı yardımıyla kolaylıkla sa÷lanmaktadır. Bu özellikten, sinüs ve
kosinüs fonksiyonlarının, baúka bir deyiúle 90o faz farklı iúaretlerin üretilmesi
amacıyla yararlanılabilir. Hareket noktası olarak herhangi bir iúaret üretecinin
üçgen dalga çıkıúını ele alalım. Bu iúaret bir gerilim karúılaútırıcının giriúine
uygulansın. Karúılaútırıcı çıkıúındaki karedalga iúareti ile üçgen dalga arasında 90o
derece faz farkı bulunur. Ikinci bir integral alıcı yardımıyla bu kare dalga iúareti
üçgen dalgaya çevrilir; bu üçgen dalga da orijinal üçgen dalgaya göre 90o farklı
olur. Devrenin ne úekilde kurulaca÷ı ùekil-3.42'de gösterilmiútir.
ENDÜSTRøYEL ELEKTRONøK
108
R3
R2
+
OP1
R1
R
+VOP1
C
+
OP2
+
OP3
+VOP2
C
+
OP4 +VOP4
R
+VOP3
ùekil-3.42. Aynı anda 90o derece faz farklı üçgen ve karedalga üreten üreteçler.
OP1 ve OP2 iúlemsel kuvvetlendiricileri ile kurulan düzen, daha önceki bölümlerde
ele alınan türden bir fonksiyon üreteci oluútururlar. OP3 ile kurulan karúılaútırıcı
fazı 900 kaydırılmıú karedalgayı, OP4 ile kurulmuú olan integral alıcı ise bununla
iliúkili üçgen dalgayı üretir.
V O1
t
V O2
t
V O3
t
VO4
t
ùekil-3.43. Dalga úekilleri.
R3 direnci üzerinden oluúturulan geribesleme olmadan devre çalıúmaz. OP4
integratörü, R3 direncinin devrede bulunmaması durumunda, kaçınılmaz olarak,
simetri ve dengesizlik hataları nedeniyle kırpma sınırlarından birine sürülürdü. Bu
olay, R3 direnci yardımıyla önlenmiú olmaktadır. R3 direnci üzerinden VO2 gerilimi
pozitif yahut negatif de÷erlere dö÷ru kaydırılır ve bununla da VO3 geriliminin
LøNEER OLMAYAN UYGULAMALAR
109
darbe-boúluk oranı de÷iúir. Böylece, VO4 geriliminin kırpılma sınırlarına kayması
önlenir; bunun do÷ru bileúeni pratik olarak sıfır olur.
VO4 çıkıúındaki üçgen dalga OP1 ve OP2 ile kurulan fonksiyon üretecinin
çalıúmasını etkilemez. VO2 geriliminin tepe de÷erlerinde VO4 sıfır olur ve OP1 ile
kurulrn Schmitt tetikleme devresini bu anda etkilemez. Devreye iliúkin dalga
úekilleri ùekil-3.43'de verilmiútir.
KAYNAKLAR
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
SIMPSON, C.D:, Industrial electronics, Prentice Hall, Englewood
Cliffs,1996.
HUMPHRIES, J., and SHEETS, L. P., Industrial Electronics, Breton
Publishers, 1983.
GREBENE, A.B., Bipolar and MOS analog integrated circuit design,
John Wiley and Sons Inc., New York, 1984.
TIETZE, U. and SCHENK, Ch., Halbleiterschaltungstechnik,
Springer Verlag, 1983.
HERPY, M., Analog integrated circuits, John Wiley and Sons, 1980.
TIETZE, U. and SCHENK, Ch., Advanced electronic circuits ,
Springer Verlag, 1978.
STANLEY, W.D., Operational amplifiers with linear integrated
circuits, Merrill Publishing Company, 1989.
REGTIEN, P.P.L., Instrumentation electronics, Prentice Hall,
Englewood Cliffs, 1992.
ALLEN, P.E. and HOLBERG,D.R., CMOS analog circuit design,
Holt-Rinehart and Winston Inc. 1987.
KUNTMAN, H., Analog tümdevre tasarımı, Sistem yayınları, 1992.
HELFRICK, A.D. and COOPER, W.D., Modern Electronic
Instrumentation and measurement techniques, Prentice Hall, 1990.
110
ENDÜSTRøYEL ELEKTRONøK