prof.dr. murat demir aydın

PROF.DR. MURAT DEMİR AYDIN
***Bu ders notları bir sonraki slaytta verilen kaynak kitaplardan alıntılar yapılarak hazırlanmıştır.
Mühendisler için Vektör Mekaniği:
STATİK
F.P. Beer, E.R. Johnston
Mühendislik Mekaniği : STATİK
R.C. HIBBELER
Çeviri Editörü: Ömer GÜNDOĞDU
Mühendislik Mekaniği : STATİK
Mühendislik Mekaniği : STATİK
J.L. Meriam, L.G. Kraige
Mehmet H. OMURTAG
Çeviri Editörü: M. Kemal APALAK
İÇİNDEKİLER
1. Temel Kavramlar
2. Parçacıkların Statiği
•
•
Düzlemdeki Kuvvetler,
Uzaydaki Kuvvetler,
3. Rijit Cisimler: Denk Kuvvet Sistemleri
4. Rijit Cisimlerin Dengesi
5. Geometrik ve Ağırlık Merkezi
6. Yapıların Analizi
7. Kirişler
8. Atalet Momentleri
9. Sürtünme
1
TEMEL KAVRAMLAR
Mühendislik Mekaniği
Katı Cisimlerin Mekaniği
Akışkanlar Mekaniği
Şekil Değiştirebilen Cisimler
Rijid Cisimler
Statik
Dinamik
Maddesel nokta (parçacık) ve rijit cisim
Uzay, referans eksen takımı ve zaman
Mutlak ve Bağıl hareket
Newton’un Kanunları
I. Kanun (Eylemsizlik prensibi): Bir maddesel
nokta, üzerine herhangi bir dengelenmemiş kuvvet
etki etmiyorsa hareketsiz kalır veya düzgün
doğrusal hareket yapmaya devam eder.
II. Kanun: Bir maddesel noktanın ivmesi, ona etki eden bileşke
kuvvet ile doğru orantılıdır ve aynı yöndedir.
III. Kanun (Etki-tepki prensibi): Birbirine kuvvet uygulayan iki cisim
arasındaki etki ve tepki kuvvetleri, birbirine eşit şiddette, zıt yönde
ve aynı tesir çizgisindedir.
Newton’un Gravitasyonel Çekim Kanunu
Uzaydaki cisimler birbirlerine çekim kuvveti
uygular. Herhangi iki cisim arasındaki çekim
kuvveti;
−𝟏𝟐 𝒎𝟑 /𝒌𝒈. 𝒔𝟐
𝒎𝟏 𝒎𝟐
𝑮
=
𝟔𝟔,
𝟕𝟑.
𝟏𝟎
𝑭=𝑮
𝒓𝟐
Uzaydaki iki cisimden birisi dünya olsun ve diğeri de dünya
yüzeyinde veya dünyaya yakın civarda bulunan bir cisim olsun.
Dünyanın bu cisme uyguladığı çekim kuvvetine ağırlık denir.
𝒎𝟏 𝒎
𝑭=𝑮 𝟐
𝒓
𝒎𝟏
𝒈=𝑮 𝟐
𝒓
𝑾 = 𝒎. 𝒈
Bu derste yer çekimi ivmesi g= 9,81 m/s2 alınacaktır. Bununla
birlikte bu değerin değişebildiği akıldan çıkarılmamalıdır.
1 kg’lık bir kütle dünya yüzeyinde 9.825 N, yüzeyden 1 km’de
9.822 N, 100 km’de 9.523 N, 1000 km’de 7.340N ve 6371 km’de
(dünyanın yarıçapı kadar) 2.456 N gelir. Böylece yüksekten uçan
roket ve füzeler için g faktörünün yükseklikle değişmesi
gerektiğinin önemi ortaya çıkar. Diğer dikkat edilmesi gereken
nokta bulunan enlemde g’nin hesaplanmasında dikkate alınan bir
parametredir.
g = 9.780 327(1 + 0.005 279 sin2 γ + 0.000 023 sin4 γ + · · ·)
γ; Enlem
Birimler ve Boyutlar : SI sisteminde temel boyutlar ve bunların
birimleri sırasıyla şu şekildedir: Bazı fiziksel büyüklüklerin
boyutları ve SI sistemindeki birimleri
Bazı fiziksel büyüklüklerin boyutları ve SI sistemindeki birimleri
Skalerler: Pozitif veya negatif sayılarla şiddeti veya büyüklüğü belirlenen
fakat bir yönle ilişkilendirilmeyen parameterelerdir. Örneğin; kütle, hacim,
sıcaklık, uzunluk, yoğunluk ve enerji. V, m, T
Vektörler: Şiddeti ve yönü ile belirlenen ve paralelkenar kuralına göre
toplanan parametrelerdir. Örneğin; yer değiştirme, hız, kuvvet, ivme,
moment.
*Vektörler kalın harfler ile veya harf
üzerinde ok işaretiyle sembolize edilirler.
*Vektörlerin şiddeti veya büyüklükleri;
𝑭, 𝑭
𝑭, 𝒂, 𝒗
𝒗, 𝒗
𝑣, 𝑎, 𝐹
𝒂, 𝒂
Eşit vektörler aynı büyüklük
ve doğrultuya sahiptirler.
Vektör İşlemleri
Negatif vektör: Verilen bir
vektör ile aynı büyüklükte
fakat zıt yönlüdür.
Kayan vektör: Kendisi ile aynı
doğrultuda olmak üzere
istenilen herhengi bir noktaya
uygulanabilen vektörlerdir.
• Bir vektörle bir skalerin çarpımı yine bir
vektördür
C
B
C
B
• Paralelkenar kuralı
• Üçgen kuralı
Sinüs Teoremi:
c
A
b
A
B
C


sin a sin b sin c
B
C
Kosinüs Teoremi:
a
C  A2  B2  2AB cosc
Kuvvet Vektörü: Bir cismin diğer bir cisme
etkisidir. Uygulama noktası, şiddeti, doğrultusu ve
yönü ile tanımlanır ve vektörel bir büyüklüktür.
Örnek 1: Şekildeki kanca F1 ve F2
kuvvetlerine
maruzdur.
Bileşke
kuvvetin şiddeti ve doğrultusunu
belirleyiniz.
FR kosinüs teoreminden,  ise sinüs teoreminden belirlenebilir.  =  + 15o
FR  (100) 2  (150) 2  2(100)(150)cos115 0
FR  10000  22500  30000( 0.4226)
FR  212.6N  213N
150
212.6

sin  sin1150
150
sin  
(0.9063)  0.6394
212.6
  sin 1 (0.6394)  39.750  39.80
    150
Bileşke kuvvetin şiddeti 213 N ve yönü yatayla 54.8o açı yapar.
Vektörün Bileşenlere Ayrılması
• Bir kuvvet vektörü, paralel kenar kuralını kullanarak etki çizgileri
bilinen iki bileşene ayrılabilir.
Örnek 2: Şekildeki 600 Newtonluk kuvvetin
u ve v doğrultularındaki bileşenlerini
belirleyiniz.
Bileşenin şiddetinin, bileşke kuvvetin şiddetinden büyük olabileceğine
özellikle dikkat etmelidir.
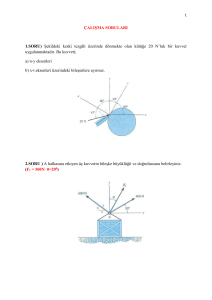
Örnek 3: İki römorkör ile çekilen mavna.
Römorkörlerin
uyguladıkları
kuvvetlerin
bileşkesi mavna ekseni doğrultusunda 25 kN
olduğuna göre,
a) a = 45o için her bir halattaki çeki kuvvetini,
b) 2. halattaki kuvvet minimum olacak şekilde a
açısını belirleyiniz.
a)
T1
T2
25 kN


sin 45 sin 30 sin 105
T1  18.5 kN T2  12.94 kN
b)
2. halatta en küçük çekiyi veren açı üçgen kuralı a’daki
değişimin etkisi gözlemlenerek bulunabilir.
2. halatta minimum çeki T1 ve T2 birbirine dik
iken oluşur.
T2  25 kNsin 30
T1  25 kNcos30
T2  12.5 kN
T1  21.65 kN
a  90  30
a  60
Kartezyen Birim
Vektör: Kartezyen eksen takımında pozitif eksenler
(x, y, z) doğrultusunda yönlenmiş bir birim şiddetindeki vektörler birim
vektörler (𝒊, 𝒋, 𝒌) olarak isimlendirilir.
𝑭 = 𝑭𝒙 +𝑭𝒚
𝑭𝒚
𝑭 = 𝑭𝒙 . 𝒊+𝑭𝒚 . 𝒋
𝑭
𝑭𝒙
𝑭 𝒙 = 𝑭𝒙 . 𝒊
𝐹= 𝑭 =
Örnek 4: Şekilde gösterilen F1
kuvvetlerini Kartezyen vektörler
belirleyiniz.
ve F2
olarak
𝑭 𝒚 = 𝑭𝒚 . 𝒋
𝑭𝒙
𝟐
+ 𝑭𝒚
𝟐
Düzlemsel Kuvvetlerin Bileşkesi
=
   
R  PQ S


R  Rx i  R y j
Her vektörü dik bileşenlerine ayırıp toplayabiliriz.






R  Px i  Py j  Qx i  Q y j  S x i  S y j


 
 





P
Rx  Px  Qx  S x
  Fx
Q




Rx i  R y j  Px  Qx  S x i  Py  Q y  S y  j
S
R y  Py  Q y  S y
  Fy
Bileşkenin büyüklüğü ve yönünü bulmak için,
R  Rx2  R y2
  tan 1
Ry
Rx
Örnek 5: A cıvatasına dört kuvvet
etkimektedir. Cıvataya etkiyen bileşke
kuvveti bulunuz.
ÇÖZÜM: Her bir kuvvet dik bileşenlerine ayrılır.
Kuvvet Şiddet

F 1 150

F2
80

F 3 110

F4
100
x  bileşen
 129 . 9
 27 . 4
0
 96 . 6
R x  199.1
y  bileşen
 75 . 0
 75 . 2
 110 . 0
 25 . 9
R y  14.3
Uygun kuvvet bileşenleri toplanarak
bileşkenin bileşenleri belirlenir.
Şiddeti ve yönü hesaplanır.
R  199.12  14.32
14.3 N
tan a 
199.1 N
R  199.6 N
a  4 .1 
Örnek 6: Braket üzerine üç kuvvet etki
etmektedir. Bileşke kuvvetin doğrultusunun
pozitif x’ ekseni yönünde ve büyüklüğünün 1 kN
olması için F1’in büyüklüğü ve  doğrultusu ne
olmalıdır?
ÇÖZÜM: Her bir kuvvet dik bileşenlerine ayrılır.

 F sin  30 



FRx   Fx : 1000cos 30o  200  450 cos 45o  F1 cos   30o
  FRy   Fy :  1000sin 30o  450sin 45o


F cos  30   347.827
F1 sin   30o  818.198
o
1
  30o  66.97o ,
F1  889 N
  37o
o
1
