Sıkıştırılamaz Viskoz İç Akış - İTÜ Gemi İnşaatı ve Deniz Bilimleri

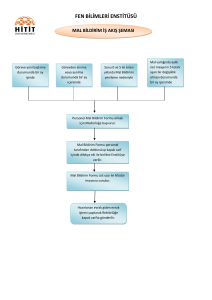
AKM 202
Akışkanlar Mekaniği
Ders Notları
8 .Bölüm
Sıkıştırılamaz Viskoz İç Akış
İTÜ
Gemi İnşaatı ve Deniz Bilimleri Fakültesi
Hazırlayan
Yrd. Doç. Dr. Şafak Nur Ertürk
Oda No:417
Tel: (212) 285 6382
e-posta: erturk@itu.edu.tr
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
Giriş
İç akışlar laminer veya türbülanslı olabilir. Bazı laminer akışlar analitik olarak çözülebilirler.
Ancak, türbülanslı akışların analitik olarak çözülebilmeleri mümkün değildir; yarı ampirik
teoriler ve deneysel veriler kullanılarak yorumlanmalıdır. İç akışlar için, akış rejimi (laminer
veya türbülanslı) Reynolds sayısının bir fonksiyonudur.
8.1 Temel Kavramlar
8.2 Parale Plakalar Arasında Tam Oluşmuş Laminer Akış
8.2.1 Her İki Plakanın Sabit Olduğu Durum
Yüksek basınçlı , hidrolik sistemlerdeki akışkan genellikle piston ve silindir arasındaki küçük
boşluktan sızar. 0.005mm'den küçük aralıklarda, bu akış alanı sonsuz paralel plakalar
arasındaki akış gibi modellenebilir.
Sonsuz paralel plakalar arasında tam oluşmuş laminer akışı gözönüne alalım. Plakalar
arasındaki mesafe a olsun. Plakalar z-yönünde sonsuza uzanmaktadırlar, ve z-yönünde
akışkan özelliklerinden hiçbiri değişim göstermez.Akış daimi ve sıkıştırılamazdır.
Hızın x-bileşeni üst ve alt plakalarda sıfır olmalıdır (kayma yok). sınır koşulları
y = 0'da,
y = a'da,
u =0
u=0
Akış tam oluşmuş olduğundan, x yönünde değişim göstermez, sadece y'ye bağlıdır, yani
u=u(y). Ayrıca y ve z yönlerinde hız bileşenleri sıfırdır. (v=w=0).
d∀ = dxdydz büyüklüğünde bir kontrol hacmi seçersek ve momentum denkleminin x
bileşenini uygularsak,
FSx + FBx =
© 2003, Şafak Nur ERTÜRK
r r
∂
u
ρ
d
∀
+
u
ρ
V
∫
∫ .dA
∂t CV
CS
8-5
(4.19a)
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
Kabuller:
1) Daimi akış
2) Tam oluşmuş akış
3) FBx=0
Tam oluşmuş akış için, kontrol yüzeyinden geçen net momentum akışı sıfırdır. x yönünde
bünyesel kuvvetler olmadığı için momentum denklemi şu hali alır:
FSx = 0
(8.2)
Bundan sonraki adım, x yönünde kontrol hacmine etki eden kuvvetleri toplamaktır. Normal
kuvvetler (basınç kuvvetleri) sağ ve sol yüzlere etkirken, teğetsel kuvvetler (kayma
kuvvetleri) üst ve alt yüzlere etkimektedir.
Parçacığın merkezindeki basınç p ise, sol yüze etkiyen basınç kuvveti
∂p dx ⎞
⎛
⎜p−
⎟dydz
∂x 2 ⎠
⎝
sağ yüze etkiyen basınç kuvveti
∂p dx ⎞
⎛
⎜p+
⎟ dydz
∂x 2 ⎠
⎝
Elemanın merkezindeki kayma gerilmesi τ yx ise, alt yüze etkiyen kayma kuvveti
dτ yx dy ⎞
⎛
⎟dxdz
− ⎜⎜τ yx −
⎟
2
dy
⎝
⎠
ve üst yüze etkiyen kayma kuvveti
dτ dy ⎞
⎛
⎜τ yx + yx
⎟dxdz
⎜
dy 2 ⎟⎠
⎝
τ yx kayma gerilmesini elemanın merkezietrafında Taylor Serisine açarken, kısmi türev yerine
toplam türevi kullandığımıza dikkat edelim. Bunu τ yx de u=u(y) gibi sadece y'nin fonksiyonu
olduğu için yaptık.
Her yüze etkiyen kuvvetleri 8.2 denkleminde yerine koyarsak,
© 2003, Şafak Nur ERTÜRK
8-6
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
FSx = 0
−
∂p dτ yx
+
=0
dy
∂x
veya
dτ yx
dy
=
∂p
∂x
(8.3)
8.3 denklemi tüm x ve y değerleri için geçerli olmalıdır. Buna göre,
dτ yx
dy
∂p
= sabit
∂x
=
Bu denklemin integrelini alırsak
⎛ ∂p ⎞
⎟ y + c1
⎝ ∂x ⎠
τ yx = ⎜
Bu da kayma gerilmesinin y ile lineer olarak değiştiğini gösterir. Newton tipi akışkan için
τ yx = µ
du
dy
(2.10)
olduğuna göre
µ
du ⎛ ∂p ⎞
= ⎜ ⎟ y + c1
dy ⎝ ∂x ⎠
ve
u=
1 ⎛ ∂p ⎞ 2 c1
⎜ ⎟ y + y + c2
2 µ ⎝ ∂x ⎠
µ
(8.4)
c1 ve c2 sabitlerini bulmak için sınır koşullarının uygularız.
y = 0'da,
u =0
y = a'da,
u=0
0=
o zaman c2=0
1 ⎛ ∂p ⎞ 2 c1
⎜ ⎟a + a
2 µ ⎝ ∂x ⎠
µ
buradan
1 ⎛ ∂p ⎞
c1 = − ⎜ ⎟a
2 ⎝ ∂x ⎠
Buna göre (8.4) denklemi
© 2003, Şafak Nur ERTÜRK
8-7
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
u=
AKM 202 AKIŞKANLAR MEKANİĞİ
1 ⎛ ∂p ⎞ 2
1 ⎛ ∂p ⎞
⎜ ⎟y −
⎜ ⎟ay
2 µ ⎝ ∂x ⎠
2 µ ⎝ ∂x ⎠
veya
u=
2
a 2 ⎛ ∂p ⎞ ⎡⎛ y ⎞ ⎛ y ⎞⎤
⎢
⎜ ⎟ ⎜ ⎟ − ⎜ ⎟⎥
2µ ⎝ ∂x ⎠ ⎢⎣⎝ a ⎠ ⎝ a ⎠⎥⎦
(8.5)
Bu da bize hız profilini verir. Akış hakkında başka ne öğrenebiliriz?
Kayma Gerilmesi Dağılımı
1 ⎛ ∂p ⎞
⎛ ∂p ⎞ ⎡ y 1 ⎤
⎛ ∂p ⎞
⎛ ∂p ⎞
⎟ y + c1 = ⎜ ⎟ y − ⎜ ⎟a = a⎜ ⎟ ⎢ − ⎥
2 ⎝ ∂x ⎠
⎝ ∂x ⎠ ⎣ a 2 ⎦
⎝ ∂x ⎠
⎝ ∂x ⎠
τ yx = ⎜
(8.6.a)
Hacimsel Akış Hızı
r r
Q = ∫ V .dA
A
z yönündeki l derinliği için
a
Q = ∫ u.l.dy
a
(
)
Q
1 ⎛ ∂p ⎞ 2
=∫
⎜ ⎟ y − ay dy
l 0 2 µ ⎝ ∂x ⎠
veya
0
Böylece l derinliği için hacimsel akış hızı
Q
1 ⎛ ∂p ⎞ 3
=−
⎜ ⎟a
l
12 µ ⎝ ∂x ⎠
(8.6b)
Basınç Düşüşünün Fonksiyonu Olarak Akış Hızı
∂p
∂x
sabit olduğundan, basınç x ile lineer olarak değişmektedir.
∆p
∂p p 2 − p1
=
=−
L
L
∂x
Hacimsel akış hızı için verilen denklemin içine yerleştirirsek,
Q
1 ⎛ − ∆p ⎞ 3 a 3 ∆p
=−
⎜
⎟a =
l
12 µ ⎝ L ⎠
12 µL
© 2003, Şafak Nur ERTÜRK
8-8
(8.6c)
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
Ortalama Hız
V ortalama hız aşağıdaki şekilde verilir.
V =
Q
1 ⎛ ∂p ⎞ a 3l
1 ⎛ ∂p ⎞ 2
=−
=−
⎜ ⎟
⎜ ⎟a
A
12µ ⎝ ∂x ⎠ la
12µ ⎝ ∂x ⎠
(8.6d)
Hızın Maksimum Olduğu Nokta
Hızın maksimum olduğu noktayı bulmak için ∂u
∂y
'yi sıfıra eşitlersek, y değerini çözeriz.
(8.5) denkleminden
du a 2 ⎛ ∂p ⎞ ⎡ 2 y 1 ⎤
=
−
⎜ ⎟
dy 2 µ ⎝ ∂x ⎠ ⎢⎣ a 2 a ⎥⎦
du
=0
dy
olursa
y=
a
2
olur
2
a ⎤
a
a 2 ⎛ ∂p ⎞ ⎡ (a 2 )
y = ' de u = u max =
⎜ ⎟⎢ 2 − 2 ⎥
a⎥
2
2 µ ⎝ ∂x ⎠ ⎢ a
⎣
⎦
1 ⎛ ∂p ⎞ 2 3
=−
⎜ ⎟a = V
8µ ⎝ ∂x ⎠
2
(8.6e)
[ ]
Koordinat Dönüşümü
Önceki bağıntıların çıkarılışı sırasında koordinat merkezi, y=0, alt plaka üstünde seçilmişti.
Koordinat merkezini kanalın merkezine oturtabiliriz. Yeni koordinat sistemimizde x, y' için
sınır koşulları,
u=0
y' = ± a
2
olur
x ve y' cinsinden hız profilini elde etmek için (8-5) denkleminde y = y '+ a
2
değerini yerine
koyarız.
u=
2
a 2 ⎛ ∂p ⎞ ⎡⎛ y ' ⎞
1⎤
⎜ ⎟ ⎢⎜ ⎟ − ⎥
2µ ⎝ ∂x ⎠ ⎢⎣⎝ a ⎠
4 ⎥⎦
(8.7)
Bu denklemden de görüleceği üzre, elde ettiğimiz hız profili Şekil 8-3'de gösterildiği gibi
paraboliktir.
© 2003, Şafak Nur ERTÜRK
8-9
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
Şekil 8- 1 Sonsuz paralel plakalar arasında tam oluşmuş laminer akış için boyutsuz hız profili.
Tüm gerilmeler Newton'un viskozite yasası gereğince hız gradyentlerine bağlandığı ve
türbülanslı salınımlar sonucu ortaya çıkan ek gerilmeler hesaba katılmadığı için, bu
bölümdeki tüm sonuçlar sadece laminer akış için geçerlidir. Deneyler göstermiştir ki, 1400'ü
geçen Reynolds sayısı için ( Re = ρV a / µ olarak tanımlı) buu akış türbülanslı hale gelir.
Çözümlerden sonra Re sayısı kontrol edilmelidir.
8.2.2 Üstteki Plakanın Sabit U Hızıyla Hareket Ettiği Durum
İçteki silindir sabit bir parça içinde dönmektedir. Hafif yüklerde, her iki parçanın merkezi
çakışmaktadır, ve aradaki boşluk simetriktir. Boşluk çok küçük olduğuna göre, bunu
modellemek için paralel plakalar arasındaki akış kullanılabilir.
r
Üstteki plakanın sağa doğru sabit U hızıyla hareket ettiğini düşünelim. Burada sadece sınır
koşulları değişmiş oldu. Hareketli plaka için sınır koşulları,
y = 0' da,
y = a' da,
u=0
r
u =U
Sadece sınır koşulları değiştiğinden (8.4) denklemini kullanabiliriz. Burada c1 ve c2 sabitlerini
bulmalıyız.
u=
© 2003, Şafak Nur ERTÜRK
1 ⎛ ∂p ⎞ 2 c1
⎜ ⎟ y + y + c2
2 µ ⎝ ∂x ⎠
µ
8-10
(8.4)
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
y = 0' da,
u=0
r
u =U
y = a' da,
U=
Buradan
c1 =
AKM 202 AKIŞKANLAR MEKANİĞİ
c2=0
1 ⎛ ∂p ⎞ 2 c1
⎜ ⎟a + a
2 µ ⎝ ∂x ⎠
µ
Uµ 1 ⎛ ∂p ⎞
− ⎜ ⎟a
2 ⎝ ∂x ⎠
a
u=
ve
Uy
1 ⎛ ∂p ⎞ 2 1 ⎛ ∂p ⎞
+
⎜ ⎟y −
⎜ ⎟ay
a 2 µ ⎝ ∂x ⎠
2 µ ⎝ ∂x ⎠
u=
2
Uy a 2 ⎛ ∂p ⎞ ⎡⎛ y ⎞ ⎛ y ⎞⎤
+
⎜ ⎟ ⎢⎜ ⎟ − ⎜ ⎟⎥
a 2 µ ⎝ ∂x ⎠ ⎢⎣⎝ a ⎠ ⎝ a ⎠⎥⎦
(8.8)
Sabit üst plaka için (u=0), (8.8) denklemi (8.5) denklemine dönüşür.
Kayma Gerilmesi Dağılımı
τ yx == µ
U
⎛ ∂p ⎞ ⎡ y 1 ⎤
+ a⎜ ⎟ ⎢ − ⎥
a
⎝ ∂x ⎠ ⎣ a 2 ⎦
(8.9.a)
Hacimsel Akış Hızı
r r
Q = ∫ V .dA
z yönünde l derinliği için,
A
z yönündeki l derinliği için
(
a
Q = ∫ u.l.dy
)
a⎡
⎤
Q
Uy a 2 ⎛ ∂p ⎞ 2
= ∫⎢ +
⎜ ⎟ y − ay ⎥dy
l 0 ⎢⎣ a 2µ ⎝ ∂x ⎠
⎦⎥
veya
0
Böylece l derinliği için hacimsel akış hızı
Q Ua
1 ⎛ ∂p ⎞ 3
=
−
⎜ ⎟a
l
2 12 µ ⎝ ∂x ⎠
(8.9b)
Ortalama Hız
V ortalama hız aşağıdaki şekilde verilir.
V =
Q ⎡Ua
1 ⎛ ∂p ⎞ 3 ⎤ l U
1 ⎛ ∂p ⎞ 2
=⎢
−
⎜ ⎟a
⎜ ⎟a ⎥ = −
A ⎣ 2 12 µ ⎝ ∂x ⎠ ⎦ la 2 12 µ ⎝ ∂x ⎠
© 2003, Şafak Nur ERTÜRK
8-11
(8.9c)
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
Hızın Maksimum Olduğu Nokta
Hızın maksimum olduğu noktayı bulmak için ∂u
∂y
'yi sıfıra eşitlersek, y değerini çözeriz.
(8.8) denkleminden
du U a 2 ⎛ ∂p ⎞ ⎡ 2 y 1 ⎤ U
a ⎛ ∂p ⎞ ⎡ ⎛ y ⎞ ⎤
= +
⎜ ⎟⎢ 2 − ⎥ = +
⎜ ⎟ 2⎜ ⎟ − 1
dy a 2 µ ⎝ ∂x ⎠ ⎣ a
a ⎦ a 2 µ ⎝ ∂x ⎠ ⎢⎣ ⎝ a ⎠ ⎥⎦
du
=0
dy
olursa
U
a
a
Uµ
a
y= −
= −
olur
2 ⎛ 1 ⎞⎛ ∂p ⎞ 2 a⎛ ∂p ⎞
⎜ µ ⎟⎜ ∂x ⎟
⎜ ∂x ⎟
⎝
⎠⎝
⎠
⎝
⎠
Maksimum hız umax ve ortalama hız V arasında basit bir bağıntı yoktur. (8.8) denklemi hız
profilinin lineer ve parabolik olduğunu gösterir. Sonuç, hız profilleri ailesidir.
Bu bölümde çıkarılan sonuçlar laminer akış için geçerlidir. Deneyler sonucu Re'nin 1500
olduğu noktada ( ∂p
∂x
= 0 için) türbülans başladığı gözlemlenmiştir. Basınç gradyentinin sıfır
olmadığı durumlar için çok fazla bilgi mevcut değildir.
8.3 Boru İçinde Tam Oluşmuş Laminer Akış
Burada akış eksenel simetriktir. Bu nedenle silidirikkoordinatlarda çalışmak daha uygundur.
Yine diferansiyel bir kontrol hacmi kullanalım, bu kez bu kontrol hacmi Şekil 8.6'da
gösterildiğigibi diferansiyel bir halka olsun. Diferansiyel kontrol hacmi uzunluğu dx ve
kalınlığı dr'dır.
Şekil 8- 2. Bir boru içinde tam oluşmuş laminer akışın analizi için kullanılan kontrol hacmi.
Tam oluşmuş daimi akış için, momentum denkleminin x bileşeni (4.19a denklemi diferansiyel
kontrol hacmine uygulandığında) , aşağıdaki hali alır.
© 2003, Şafak Nur ERTÜRK
8-12
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
FSx = 0
Bir sonraki adım, x yönünde kontrol hacmine etkiyen tüm kuvvetleri toplamaktır. Normal
kuvvetler (basınç kuvvetleri) kontrol hacmiin sağ ve sol uçlarına etkimektedir; teğetsel
kuvvetler (kayma kuvvetleri) ise iç ve dış silidiik yüzeylere etkimektedir.
Kontrol hacminin merkezindeki basınç p ise, sol uçtaki basınç kuvveti
∂p dx ⎞
⎛
⎜p−
⎟2πrdr
∂x 2 ⎠
⎝
olacaktır.
Sağ uçtaki basınç kuvveti
∂p dx ⎞
⎛
−⎜ p+
⎟2πrdr dır.
∂x 2 ⎠
⎝
Kontrol hacminin merkezindeki kayma gerilmesi τ rx ise, içteki silindir yüzeyi üzerindeki
kayma kuvveti
dτ dr ⎞ ⎛
dr ⎞
⎛
− ⎜τ rx − rx
⎟2π ⎜ r − ⎟dx
2⎠
dr 2 ⎠ ⎝
⎝
Dıştaki silindir yüzeyi üzerindeki kayma kuvveti
dτ dr ⎞ ⎛
dr ⎞
⎛
⎜τ rx + rx
⎟2π ⎜ r + ⎟dx
2⎠
dr 2 ⎠ ⎝
⎝
olacaktır.
Kontrol hacmine etkiyen kuvvetlerin x bileşeninin toplamı sıfır olmalıdır. O zaman
−
dτ
∂p
1 d (rτ rx )
2πrdr + τ rx 2πrdrdx + rx =
∂x
dr
r dr
(8.10)
τ rx sadece r'nin fonksiyonu olduğu için (ki bu nedenle kısmi türev yerine toplam türevi
kullandık) (8.10) denklemi ancakdenklemin her iki tarafı da sabit olursa tüm r ve x değerleri
için geçerli olur. O zaman
1 d (rτ rx ) ∂p
=
= sabit
∂x
r dr
veya
d (rτ rx )
∂p
=r
dr
∂x
Her iki tarafın integralini alırsak,
© 2003, Şafak Nur ERTÜRK
8-13
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
r 2 ⎛ ∂p ⎞
=
⎜ ⎟ + c1
2 ⎝ ∂x ⎠
rτ rx
veya
r ⎛ ∂p ⎞ c1
⎟+
2 ⎝ ∂x ⎠ r
τ rx = ⎜
Aynı zamanda τ rx = µ
du
olduğundan
dr
µ
du r ⎛ ∂p ⎞ c1
= ⎜ ⎟+
dr 2 ⎝ ∂x ⎠ r
ve
u=
r 2 ⎛ ∂p ⎞ c1
⎜ ⎟ + ln r + c 2
4µ ⎝ ∂x ⎠ µ
(8.11)
olur.
Sabit c1 ve c2 değerlerini bulmamız gerekir. Ancak sadece bir tek sınır koşulumuz var. (u=0
r=R'de) O zaman ne yapabiliriz? Borunun merkezindeki akış hızını bilmesek bile, fiziksel
olarak r=0'da hızın sonlu bir değerde olması gerektiğini biliyoruz. Bunun gerçek olabilmesi
için c1 değeri sıfır olamlıdır. Fiziksel nedenlerden dolayı c1=0 olduğunu buluruz. O zaman
u=
r 2 ⎛ ∂p ⎞
⎜ ⎟ + c2
4µ ⎝ ∂x ⎠
c2 sabitini eldeki sınır koşulunu kullanarak buluruz. r=R'de u=0'dır.
0=
R 2 ⎛ ∂p ⎞
⎜ ⎟ + c2
4µ ⎝ ∂x ⎠
O zaman
c2 = −
R 2 ⎛ ∂p ⎞
⎜ ⎟ olur.
4 µ ⎝ ∂x ⎠
Sonuç olarak,
r 2 ⎛ ∂p ⎞ R 2 ⎛ ∂p ⎞
u=
⎜ ⎟−
⎜ ⎟
4 µ ⎝ ∂x ⎠ 4 µ ⎝ ∂x ⎠
u=
(
1 ⎛ ∂p ⎞ 2
2
⎜ ⎟r −R
4 µ ⎝ ∂x ⎠
)
2
R 2 ⎛ ∂p ⎞ ⎡ ⎛ r ⎞ ⎤
u=−
⎜ ⎟ ⎢1 − ⎜ ⎟ ⎥
4 µ ⎝ ∂x ⎠ ⎢⎣ ⎝ R ⎠ ⎥⎦
© 2003, Şafak Nur ERTÜRK
8-14
(8.12)
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
Hız profilini bildiğimize göre akışa ait diğer özellikleri bulabiliriz.
Kayma Gerilmesi Dağılımı
τ rx = µ
du r ⎛ ∂p ⎞
= ⎜ ⎟
dr 2 ⎝ ∂x ⎠
(8.13a)
Hacimsel Akış Hızı
(
)
R
r r R
1 ⎛ ∂p ⎞ 2
2
Q = ∫ V .dA = ∫ u 2πrdr = ∫
⎜ ⎟ r − R 2πrdr
4
µ
x
∂
⎝ ⎠
0
0
A
Q=−
π R 4 ⎛ ∂p ⎞
⎜ ⎟
8 µ ⎝ ∂x ⎠
(8.13b)
Basınç Düşüşünün Fonksiyonu Olarak Akış Hızı
Tam oluşmuş akışta, basınç gradyenti ∂p / ∂x , sabittir. Bu nedenle,
∂p
= ( p 2 − p1 ) / L = − ∆p / L
∂x
(8.13b) denkleminde yerine koyarsak, yatay boruda laminer akış için,
πR 4
Q=−
8µ
4
π∆pD 4
⎡ ∆p ⎤ π∆pR
⎢⎣− L ⎥⎦ = 8µL = 128µL
(8.13c)
Ortalama Hız
V =
Q
Q
R2
=
=
−
A πR 2
8µ
⎛ ∂p ⎞
⎜ ⎟
⎝ ∂x ⎠
(8.13d)
Hızın Maksimum Olduğu Nokta
Hızın maksimum olduğu noktayı bulmak için du / dr 'yi sıfıra eşitleriz ve r için çözeriz. (8.12)
denkleminden
1 ⎛ ∂p ⎞
du
=
⎜ ⎟r
dr 2 µ ⎝ ∂x ⎠
© 2003, Şafak Nur ERTÜRK
8-15
8. Bölüm
DERS NOTLARI
O zaman
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
du
= 0 iser=0 olmalıdır.
dr
r=0'da
u = u max = U = −
R 2 ⎛ ∂p ⎞
⎜ ⎟ = 2V
4µ ⎝ ∂x ⎠
(8.13e)
(8.12)'deki hız profili maksimum hız cinsinden yazılabilir.
u
⎛r⎞
= 1− ⎜ ⎟
U
⎝R⎠
2
(8.14)
Bölüm B
Borular ve Kanallar İçindeki Akış
Bu bölümdeki ana hedef borular içindeki sıkıştırılamaz akış sonucu oluşan basınç
değişimlerini bulmaktır. Akış sistemlerindeki basınç değişimleri, kot farkından veya akış hızı
değişimlerinden (kesit alanı değiştiği için) ve sürtünmeden kaynaklanır. Sürtünmesiz bir
akışta, yükseklik farkları ve akış hızı farklarının etkisi Bernoulli denklemi kullanılarak
gösterilebilir. Gerçek akışların analizinde öncelikli nokta sürtünmenin hesaba katılmasıdır.
Sürtünme sonucu basınç azalır; ideal, sürtünmesiz akışa göre basınç "kaybı" meydana gelir.
Analizi sadeleştirmek için,
8.4 Tam Oluşmuş Boru Akışında Kayma Gerilmesi Dağılımı
Yatay bir borudaki tam oluşmuş daimi akışta, türbülanslı veya laminer olsun, basınç düşüşü,
boru duvarlarındaki kayma kuvvetleri ile dengelenir. Bunu Şekil 8-7'deki silindirik kontrol
hacmine momentum denklemini uygulayarak görebiliriz. Monentum denkleminin x-bileşeni
FSx + FBx =
© 2003, Şafak Nur ERTÜRK
r
∂
uρd∀ + ∫ uρV .d∀
∫
∂t CV
CS
8-16
(4.19a)
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
Şekil 8- 3…………………………………
Kabuller:
1. Yatay boru, FBx=0
2. Daimi akış
3. Sıkıştırılamaz akış
4. Tam oluşmuş akış
Bu kabuller sonucu FSx = 0 olur.
∂p dx ⎤ 2
∂p dx ⎤ 2 ⎡
⎡
πr − ⎢ p +
πr + τ rx 2πrdx = 0
FSx = ⎢ p −
⎥
∂x 2 ⎥⎦
∂x 2 ⎦
⎣
⎣
−
∂p
dxπr 2 + τ rx 2πrdx = 0
∂x
r ⎛ ∂p ⎞
⎟
2 ⎝ ∂x ⎠
τ rx = ⎜
(8.15)
Akışkan üzerindeki kayma gerilmesi boru kesitinde lineer olarak değişmektedir. Merkezde
sıfırdan boru duvarında maksimuma doğru değişir. Duvardaki kayma gerilmesini τ w ile
gösterirsek, (8.15) denklemi, borunun yüzeyinde
τ w = −[τ rx ]r = R = −
(8.16)
denkleminde
duvardaki
kayma
R ∂p
2 ∂x
gerilmesi,
olur
eksenel
(8.16)
basınç
gradyenti
ile
ilişkilendirilmiştir. Ancak, kayma gerilmesi ve hız alanı arasında bir bağıntı kurulmamıştır.
Bu nedenle (8.16) denklemi hem laminer hem de türbülanslı tam oluşmuş boru akışlarına
uygulanabilir.
8.5 Laminer Akıştaki Kayıplar
Akışkan bir noktadan diğerine hareket ederken viskoz direnci yenmek için toplam "hed
kaybı" meydana gelir.
p1
ρ
+ gz1 +
V12
p
V 2
= 2 + gz 2 + 2 + HLg
2
2
ρ
© 2003, Şafak Nur ERTÜRK
8-17
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
Bu iki nokta arasındaki tek kayıp sürtünme nedeniyle oluşur. Bunu hf ile gösterelim. Ayrıca
V1=V2 olduğundan,
p1
ρ
+ gz1 =
p2
ρ
+ gz 2 + h f g
⎞
⎛ p1
⎞ ⎛p
⎜⎜
+ gz1 ⎟⎟ − ⎜⎜ 2 + gz 2 ⎟⎟ = h f g
⎠
⎝ ρ
⎠ ⎝ ρ
1 ve 2 noktaları için,
Sp = −
Sp =
=
V =
∂ ( p + ρgz )
∂x
( p1 + ρgz1 ) − ( p1 + ρgz 2 )
L
⎞⎤ ρ
⎞ ⎛p
ρ ⎡⎛ p1
+ gz1 ⎟⎟ − ⎜⎜ 2 + gz 2 ⎟⎟⎥ = h f g
⎢⎜⎜
L ⎣⎝ ρ
⎠⎦ L
⎠ ⎝ ρ
R2
D2 ⎛ ρ
⎞
Sp =
⎜ hf g⎟
8µ
32µ ⎝ L
⎠
hf =
hf =
32 µLV
ρgD 2
⎛ µ ⎞⎛ L ⎞⎛⎜ V 2 ⎞⎟
⎟⎟⎜ ⎟
= 64⎜⎜
⎝ V Dρ ⎠⎝ D ⎠⎜⎝ 2 g ⎟⎠
64 ⎛ L ⎞⎛⎜ V 2
⎜ ⎟
ℜ ⎝ D ⎠⎜⎝ 2 g
2
⎛ L ⎞⎛ V
h f = K ⎜ ⎟⎜
⎝ D ⎠⎜⎝ 2 g
⎞
⎟
⎟
⎠
⎞
⎟
⎟
⎠
K=
64
: sürtünme sayisi
ℜ
Darcy-Weisbach Denklemi
Sabit kesitli yatay konumdaki bir borudaki tam gelişmiş akış için basınç kaybı "ana kayıp"
olarak adlandırılır. Ana kayıp, sürtünme etkisiyle mekanik enerjiden termal enerjiye
dönüşümü gösterir. Bu nedenle kayıp sadece boru içindeki akışa bağlıdır, borunun
konumundan bağımsızdır.
8.6 Türbülanslı Akıştaki Kayıplar
Laminer akış için sürtünmeden kaynaklana hed kaybı
2
⎛ L ⎞⎛⎜ V
h f = K⎜ ⎟
⎝ D ⎠⎜⎝ 2 g
⎞
⎟
⎟
⎠
© 2003, Şafak Nur ERTÜRK
8-18
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
Darcy-Weisbach Denklemi ile verilmişti. Burada K = f (ℜ) , sürtünme sayısı sadece
Reynolds sayısının bir fonksiyonuydu.
Akış laminerden türbülanslıya geçtiğinde atalet kuvvetleri önem kazanmaya başlar. Borunun
pürüzlülüğüne bağlı olarak girdaplar ve çapraz akıntılar oluşur. Deneysel çalışmalar
göstermiştir ki, türbülanslı akışta da,
2
⎛ L ⎞⎛ V
h f = K ⎜ ⎟⎜
⎝ D ⎠⎜⎝ 2 g
⎞
⎟
⎟
⎠
Darcy-Weisbach Denklemi
bağıntısı kullanılabilir. Ancak bu durumda, K sadece Reynolds sayısının bir fonksiyonu
değildir, aynı zamanda borunun pürüzlülüğüne de bağlıdır.
Yüzey pürüzlülüğü genelde bağıl pürüzlülük olarak verilir. Bağıl pürüzlülük =e/D olarak
ifade edilir. Burada e: pürüzlülük yüksekliği, ve D boru çapıdır.
e⎞
⎛
K = f ⎜ ℜ, ⎟
⎝ D⎠
1. Laminer akış için ℜ ≤ 2000
K=
64
ℜ
2. Pürüzsüz borulardaki türbülanslı akış için
1
K
(
)
= 0.86 ln ℜ K − 0.8
3. Tamamen pürüzlü yüzeyler için (K, ℜ 'den bağımsız)
⎛e⎞
= 1.14 − 0.86 ln⎜ ⎟
K
⎝D⎠
1
4. İki uç arasındaki durumda
⎛e
2.51
= −0.86 ln⎜⎜ D +
⎜ 3.7 ℜ K
K
⎝
1
© 2003, Şafak Nur ERTÜRK
8-19
⎞
⎟
⎟⎟
⎠
8. Bölüm
DERS NOTLARI
SIKIŞTIRILAMAZ VİSKOZ İÇ AKIŞ
AKM 202 AKIŞKANLAR MEKANİĞİ
8.7 Diğer Kayıplar
© 2003, Şafak Nur ERTÜRK
8-20
8. Bölüm