AĞIRLIK MERKEZİ VE ALAN
ATALET MOMENTLERİ
AĞIRLIK MERKEZİ VE ALAN ATALET
MOMENTLERİ
• Bu konular denge problemelerinden tamamen
bağımsızdır.
• Alanların ağırlık merkezi ve atalet momenti
ismi verilen geometrik özelliklerini
hesaplamaya yöneliktir.
• Bu hesaplamalar mukavemet hesaplarında
kullanılmaktadır.
AĞIRLIK MERKEZİ VE ALAN ATALET MOMENTLERİ
AĞIRLIK MERKEZİ-GEOMETRİK MERKEZ
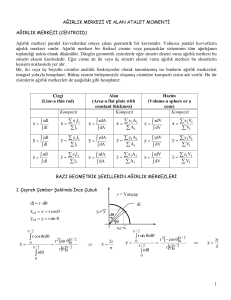
Tanım: Ağırlık merkezi G, parçacıklar sisteminde ağırlığın
bileşkesinin olduğu noktadır. Parçacıların ağırlıklarının paralel
kuvvet sistemleri olduğu düşünülür. Ağırlıklar sistemi ağırlık
sistemine konacak tek bir ağırlıkla değiştirilebilir.
Toplam Ağırlık
n
WR Wi
i 1
n
Ağırlık Merkezi:
x
xiWi
i 1
n
W
i
i 1
n
y
yiWi
i 1
n
W
i 1
i
n
z
zW
i 1
n
i
i
W
i 1
i
Eğer bir yapı sonsuz sayıda partikülden oluşuyorsa ağırlık
merkezine integral ifadeleri katılır.
x dW
dW
x
x
x dV
V
dV
V
y
y
y dW
dW
y dV
V
dV
V
z
z dW
dW
z
z dV
V
dV
V
yoğunluk
dW dV
x, y, z
xi , yi , zi
ağırlık merkezinin koordinatları
i. parçacığın koordinatı
Wi
i. parçacığın ağırlığı
Geometrik Merkez
Tanım: Bir nesnenin geometrik merkezidir. Formülasyonu ağırlık merkezine benzer. İzotropik ve
homojen cisimlerde ağırlık merkezi ile geometrik merkez aynıdır.
x
Hacimsel merkez:
Alansal merkez:
x dV
V
dV
V
x
dV
V
x dA
A
x
Çizgisel merkez:
y
y dV
V
dA
y
y dA
A
dA
A
x dL
y dL
dL
L
y
dV
V
A
L
z
z dV
V
L
dL
L
z
z dA
A
dA
A
z
z dL
L
dL
L
Örnek Problem
Üçgenin geometrik merkezini bulunuz.
ÇÖZÜM:
Üçgenin geometrik merkezini iki metodla bulabiliriz.
1. Şerit metodu:
2. Çift integral metodu:
dA dx dy
xx
yy
dA x dy
b
dA h y dy
h
1b
x h y
2h
yy
y
y dA
A
dA
A
b
h
y
dA
b
0 h h y dy
x
x dA
A
dA
A
1b
b
0 2 h h y h h y dy
h
h
b
h h y
0
1 2
b h
b
x 6
1
3
b h
2
dy
b
y
h
0
2b
2
1
2
0
h
(b x )
b b
2
b
ydydx
0
0
0
1 2
bh
h
y6
1
bh 3
2
A
A
y h h y dy
h
y dA
h
(b x )
b b
1 2
bh
h
y6
1
bh 3
2
0
2
2b 2
1
2
(b x) 2 dx
bh
dydx
0
(b x) 2 dx
bh
h
h 2
(b x)3
6b 2
1
2 bh
Temel Alanların Geometrik Merkezi:
Yarım daire
Çeyrek daire
4𝑟
𝑥=𝑦=
3𝜋
Üçgen
G, Kenar ortayların kesim
noktasındadır.
𝑥=
4𝑟
3𝜋
,
𝑦=0
𝑦=
Kare, dikdörtgen
𝑥=
𝑏
,
2
𝑦=
ℎ
2
4𝑟
3𝜋
, 𝑥=0
Tam Daire
Kompozit yapıların geometrik merkezi:
Basit yapıların (temel geometrilerin) birleşmesinden oluşmuş karmaşık yapılara
kompozit yapılar denir. Bunların geometrik merkezi bulunurken basit yapıların
geometrik merkez özelliklerinden yararlanılır.
Çözüm Yöntemi:
•
•
•
•
Karmaşık yapı basit geometrili alt parçalara ayrılır.
Eğer delik veya kesilmiş kısım varsa bunlar negatif alan gibi düşünülür.
Simetri varsa geometrik merkez bu simetri ekseni üzerindedir.
Tablo oluşturulur ve çözüm yapılır.
Alanlar için:
n
x
x A
i 1
n
i
i
A
i 1
i
n
y
y A
i 1
n
i
i
A
i 1
i
n
z
z A
i 1
n
i
i
A
i 1
i
Örnek: Şekildeki alanın geometrik merkezinin
koordinatlarını hesaplayınız.
Çözüm: x eksenine göre simetriklikten dolayı
geometrik merkezin y koordinatı sıfır «0» olur.
Örnek: Şekildeki alanın geometrik merkezinin koordinatlarını tablo kullanarak bulunuz.
Parça
Ai (mm2)
=
Ai . x i
𝑏
=− =
3
4
− =
3
24x (-1.33)=
24
−1.33
-31.92
4x8 =
8/ 2=
32
4
𝑏.ℎ
2
=
12.4
=
2
𝜋.82
=
4
50.24
−
4.𝑟
3𝜋
4.8
= =
3.𝜋
3.4
𝜋.22
=
2
-6.28
12.5
=
2
30
S
xi (mm)
129.96
-24x 0
0
0
32x4=
-4/2 =
32x(-2)=
128
-2
-64
50,24x3.4 =
170.82
4.𝑟
3𝜋
4.8
=
3.𝜋
=
3.4
-0.85
-37.68
12
=
3
4
Ai . yi
=
-6.28x6 =
6
yi (mm)
170.82
-6.28x 0.85 =
5.34
-4-y′′=
- 4- (5/3)=
120
349.22
- 5.67
-170.1
-57.94
Eylemsizlik (Atalet) Momentleri:
Eylemsizlik kuvveti, cisimlere etkiyen kuvvet. Eylemsizlik kuvveti sistemin ivmesiyle zıt yönde oluşur. Eylemsizlik
kuvveti yoktan var edilemez. Var olan enerjiyi cisim yine kendi halini yani hareketsiz haline dönmek için kendi
hareket yönüne zıt bir kuvvet oluşturup kullanır... evrende madde her zaman ilk hareketlerini korumak ister, yani
duruyorsa durmak hareket halindeyse o hızda hareke devam etmek ister. Cisme bir kuvvet uygulandığında cisim
harekete ters yönde cevap vererek ilk halini korumak isteyecektir. işte bu kuvvet eylemsizlik kuvvetidir. Bir cisme
uygulanan hiçbir kuvvet yoksa ya da cisme uygulana kuvvetlerin bileşkesi 0 ise cisim ya hareketsiz kalır ya da
düzgün doğrusal hareket yapar. Örneğin sıra üzerinde duran bir kitaba dışarıdan bir kuvvet uygulanmadıkça
sonsuza kadar bırakıldığı yerde kalır.
Başka bir cisme eşit büyüklükte zıt yönde iki kuvvet uygulanırsa kuvvetler birbirini yok edeceğinden cisim hareket
etmez. Sürtünmesiz bir ortamda bir misketi harekete geçirdiğimizde misket düzgün doğrusal hareket yapar. Duran
bir otobüste ayaktaki yolcuların haberi olmadan otobüs aniden hareket ederse yolcular arkaya doğru itilir. Hareket
halindeki bir otobüsün aniden fren yapması sonunda ayaktaki ve oturan yolcuların öne fırlamaları yolcuların
bulundukların durumları korumak istemelerinden kaynaklanır. Trafik kazalarında arabaların ön koltuklarında
oturanların ani fren sonunda kafalarını cama çarpmamaları için emniyet kemeri takmaları zorunludur. Duran bir
cismi herhangi bir kuvvet etkilemedikçe sürekli durur. Hareket halindeki bir cismi hareketini engelleyecek bir
kuvvet etki etmedikçe hareketine devam eder. Bu özelliğe eylemsizlik denir. Eylemsizlik Momenti; veya atalet
momenti (SI birimi kilogram metrekare - kg m²), dönme hareketi yapan bir cismin dönme eylemsizliğidir.
Yapı elemanlarının,
1. Eğilme
2. Burulma hesabında
3. Kesitlerde
Hesaplarında kullanılan ve I ile gösterilen
matematik bağıntıya alanın ikinci momenti
veya atalet momenti denir. Mühendislikte
olmazsa olmaz özelliklerden biridir.
Örnek: Şekilde verilen dikdörtgenin,
a. Tabandan geçen eksene göre
b. Ağırlık merkezinden geçen eksene göre atalet momentinin
bulunması.
Paralel Eksen Teoremi:
Bir eksene göre atalet momenti belli iken, bu
eksene paralel başka bir eksene göre atalet
momenti bulunabilir. Şöyle ki:
Ağırlık merkezinden geçen yatay eksene (xg ) göre
atalet momenti ( Ixg )belli iken, x eksenine göre
atalet momenti :
A: Alan, dy : eksenler arasındaki dik uzaklıktır.
Paralel eksen teoreminin uygulanması için 2
önemli şart vardır:
1- Eksenler birbirine paralel olmalıdır.
2- Bir eksen mutlaka ağıırlık merkezinden geçmelidir.
Ix bilinirken ise Ixg nin bulunması:
Benzer şekilde;
Temel Alanların Atalet Momentleri:
Yarım daire
Tam Daire
𝐼𝑥 = 𝐼𝑦 =
𝐼𝑥 = 𝐼𝑦 =
𝜋𝑟 4 𝜋.𝐷4
= 64
4
𝜋𝑟 4 𝜋.𝐷4
=
8 128
Dikkat: Ix ağırlık merkezinden değil, daire
merkezinden geçen eksene göredir.
Çeyrek daire
Kare, dikdörtgen
𝐼𝑥 = 𝐼𝑦 =
𝑏ℎ3
𝐼𝑥𝑔 =
12
ℎ𝑏3
𝐼𝑦𝑔 =
12
𝐼𝑥 =
𝐼𝑦 =
𝑏ℎ3
3
ℎ𝑏3
3
𝜋𝑟 4 𝜋.𝐷4
=
16 256
𝐷𝑖𝑘𝑡ö𝑟𝑔𝑒𝑛 𝑖ç𝑖𝑛 𝐼𝑥𝑔 𝑏𝑖𝑙𝑖𝑛𝑖𝑟𝑘𝑒𝑛 𝐼𝑥 𝑖
𝑝𝑎𝑟𝑎𝑙𝑒𝑙 𝑒𝑘𝑠𝑒𝑛 𝑡𝑒𝑜𝑟𝑒𝑚𝑖𝑛𝑑𝑒𝑛 𝑑𝑒 𝑏𝑢𝑙𝑎𝑏𝑖𝑙𝑖𝑟𝑖𝑧:
𝐼𝑥 = 𝐼𝑥𝑔 + 𝐴. 𝑑 2 =
𝑏ℎ3
12
ℎ
+ 𝑏. ℎ. ( 2 )2 =
𝑏ℎ3
3
Örnek (2009 final): Tablo kullanarak, şekildeki alanın;
a-) ağırlık merkezinin koordinatlarını,
b-) şekildeki x eksenine göre atalet momentini,
c-) ağırlık merkezinden geçen ve şekildeki x eksenine
paralel olan eksene ( 𝑥 ) göre atalet momentini hesaplayınız.
Örnek: Şekilde verilen birleşik kesitin ağırlık merkezine
göre atalet momentinin [Ix]
Çözüm:
Örnek Sorular:
Şekildeki alanların ağırlık merkezinden geçen
yatay ve düşey eksenlere göre atalet
momentlerini (𝐼𝑥𝑔 , 𝐼𝑦𝑔 ) hesaplayınız.