MANYETİK DİPOLÜN MANYETİK ALANI Rafet Kamer, Fizik öğretmeni
advertisement
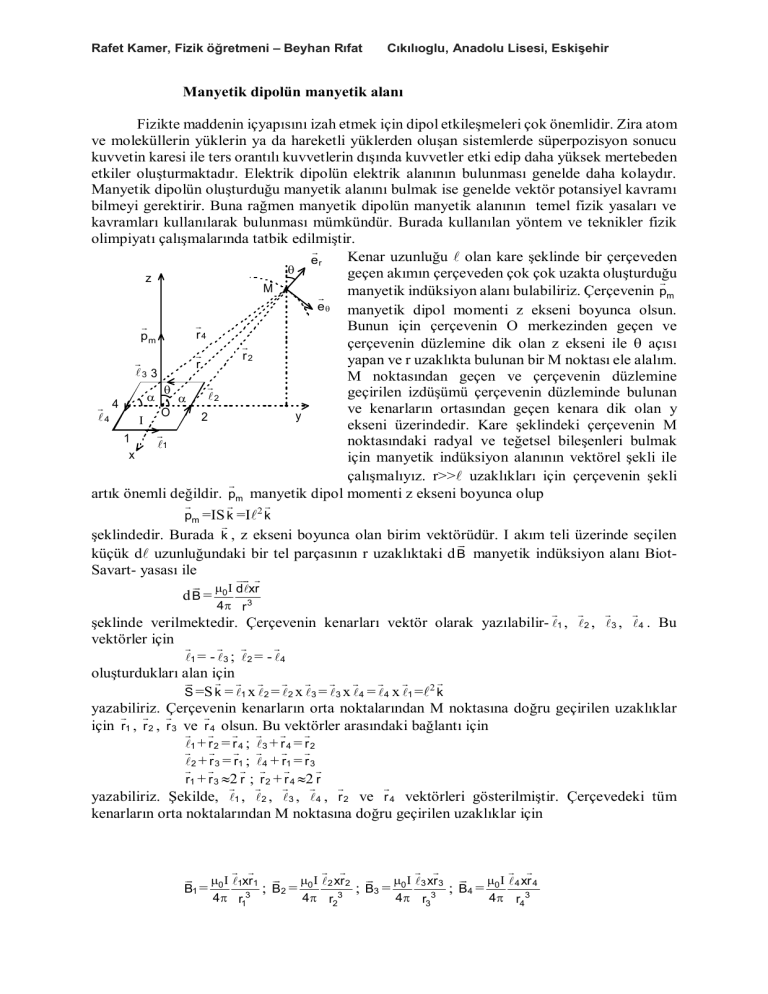
Rafet Kamer, Fizik öğretmeni – Beyhan Rıfat Cıkılıoglu, Anadolu Lisesi, Eskişehir Manyetik dipolün manyetik alanı Fizikte maddenin içyapısını izah etmek için dipol etkileşmeleri çok önemlidir. Zira atom ve moleküllerin yüklerin ya da hareketli yüklerden oluşan sistemlerde süperpozisyon sonucu kuvvetin karesi ile ters orantılı kuvvetlerin dışında kuvvetler etki edip daha yüksek mertebeden etkiler oluşturmaktadır. Elektrik dipolün elektrik alanının bulunması genelde daha kolaydır. Manyetik dipolün oluşturduğu manyetik alanını bulmak ise genelde vektör potansiyel kavramı bilmeyi gerektirir. Buna rağmen manyetik dipolün manyetik alanının temel fizik yasaları ve kavramları kullanılarak bulunması mümkündür. Burada kullanılan yöntem ve teknikler fizik olimpiyatı çalışmalarında tatbik edilmiştir. Kenar uzunluğu olan kare şeklinde bir çerçeveden er geçen akımın çerçeveden çok çok uzakta oluşturduğu z M manyetik indüksiyon alanı bulabiliriz. Çerçevenin pm e manyetik dipol momenti z ekseni boyunca olsun. Bunun için çerçevenin O merkezinden geçen ve r4 pm çerçevenin düzlemine dik olan z ekseni ile açısı r2 yapan ve r uzaklıkta bulunan bir M noktası ele alalım. r 3 3 M noktasından geçen ve çerçevenin düzlemine geçirilen izdüşümü çerçevenin düzleminde bulunan 2 4 ve kenarların ortasından geçen kenara dik olan y O y 4 2 ekseni üzerindedir. Kare şeklindeki çerçevenin M 1 noktasındaki radyal ve teğetsel bileşenleri bulmak 1 x için manyetik indüksiyon alanının vektörel şekli ile çalışmalıyız. r>> uzaklıkları için çerçevenin şekli artık önemli değildir. pm manyetik dipol momenti z ekseni boyunca olup pm =S k =2 k şeklindedir. Burada k , z ekseni boyunca olan birim vektörüdür. akım teli üzerinde seçilen küçük d uzunluğundaki bir tel parçasının r uzaklıktaki d B manyetik indüksiyon alanı BiotSavart- yasası ile dxr 0 dB = 4 r 3 şeklinde verilmektedir. Çerçevenin kenarları vektör olarak yazılabilir- 1 , 2 , 3 , 4 . Bu vektörler için 1 = - 3 ; 2 = - 4 oluşturdukları alan için S =S k = 1 x 2 = 2 x 3 = 3 x 4 = 4 x 1 =2 k yazabiliriz. Çerçevenin kenarların orta noktalarından M noktasına doğru geçirilen uzaklıklar için r1 , r 2 , r 3 ve r 4 olsun. Bu vektörler arasındaki bağlantı için 1 + r 2 = r 4 ; 3 + r 4 = r 2 2 + r 3 = r1 ; 4 + r1 = r 3 r1 + r 3 2 r ; r 2 + r 4 2 r yazabiliriz. Şekilde, 1 , 2 , 3 , 4 , r 2 ve r 4 vektörleri gösterilmiştir. Çerçevedeki tüm kenarların orta noktalarından M noktasına doğru geçirilen uzaklıklar için 0 1xr1 0 2 xr 2 0 3 xr 3 0 4 xr 4 B1 = ; B2 = ; B3 = ; B4 = 4 r13 4 r23 4 r33 4 r43 Rafet Kamer, Fizik öğretmeni – Beyhan Rıfat Cıkılıoglu, Anadolu Lisesi, Eskişehir yazabiliriz. Çerçevenin geometrik O merkezi ile M noktası arasındaki uzaklık r olsun. Çerçevenin 1. ve 3. No’lu kenarlarından M noktasına doğru geçirilen doğrularda açısına bir bağlılık yoktur. Dolayısıyla bu kenarlar için r1r3r alınılabilir. Bu iki kenarın M noktasında oluşturdukları manyetik indüksiyon alanların toplamı 0 1xr1 0 3 xr 3 0 1xr1 0 1xr 3 B13 = B1 + B3 = + = 4 r13 4 r33 4 r 3 4 r 3 0 1x r1 r 3 0 1x2 0 1x2 0 2 0 pm = = = = k= 4 4 r 3 4 r 3 r3 4 r 3 4r 3 olur. Bu iki manyetik indüksiyon alanının toplamı z ekseni boyuncadır. Çerçevenin 2. ve 4. No’lu kenarlardan M noktasına kadar olan uzaklıklarda açısına bağlı farklılıklar meydana gelir. Bu uzaklıklar için r2r- cos sin cos sin =r; r4r+ =r+ 2 2 2 2 yazabiliriz. Bu iki kenarın oluşturdukları manyetik indüksiyon alanlarının toplamı 2 xr 2 0 4 xr 4 0 0 2 xr 2 2 xr 4 B24 = B2 + B4 = 0 + 3 3 4 r23 4 r43 4 4 sin sin r r 2 2 2 xr 2 2 xr 4 0 - 0 4 3 3 sin 4 3 3 sin r 1 r 1 2r 2r 0 2 xr 2 3 sin 0 2 xr 4 3 sin 1 1 = 4 r 3 2r 4 r 3 2r 0 2 x r 2 r 4 3 sin 0 2 x3 0 2 x2r 3 sin 0 2 x r 2 r 4 = + 1 + = 4 4 4 r 4 r 3 2r r3 r3 r3 p 30 sin 2 3 sin = 0 3 k+ 0 4 2 xr = 0 m k+ 2 xr = 4r 4r 3 4r 4 4 r 0pm 30 sin 0pm 30 2 sin 0 pm 30pm sin = k+ re = k+ e = + e 4r 3 4r 4 4r 3 4r 3 4r 3 4r 3 olur. Toplam bileşke manyetik indüksiyon alanı 3 p sin p B = B13 + B24 =2 0 m + 0 m 3 e 3 4r 4r olarak bulunur. k birim vektör ve er ile e birim vektörleri için k =cos. er -sin. e ; sin. e =cos. er - k yazabiliriz. Buradan 20pm cos.er sin.e 30pm sin 20 pm cos 0pm sin B= + e er + e = 4r 3 4r 3 4r 3 4r 3 ya da 0 pm 30pm 20 pm 30pm B =2 + cos.er k = + cos.er k = 3 3 3 3 4r 4r 4r 4r 20 pm 30 pm 30pmr cos 30 pm .r er 0 pm 30 pm .r r 0 pm = + er = = = 4r 4 4r 4 4r 5 4r 3 4r 3 4r 3 4r 3 = 30 pm .r r 0 pm r.r 4r 5 - = 3 p .r r p r.r 4r 5 0 m m 4 r 5 Rafet Kamer, Fizik öğretmeni – Beyhan Rıfat Cıkılıoglu, Anadolu Lisesi, Eskişehir olarak bulunur. Bulunan bileşenlerin ifadelerini süperiletkenlerde gözlenen ve süperiletken maddelerin dış manyetik indüksiyon alanında belli B d değere kadar manyetik indüksiyon alanını maddenin dışına B0 itilme olayını açıklayabiliriz. Manyetik indüksiyon alanı belli Bdr kritik değeri aştığında ise bu süperiletken maddeler süperilet-ken özelliğini kaybetmektedir. Süperiletken madde içinde uygulanan pm dış manyetik indüksiyon alanın girememesi süper-iletken maddenin yüzeyinde akan akımlar ile modellenilebilir. Bu akımlar ise bir manyetik dipol oluşturmaktadır. Akan akımlar bir manyetik dipol oluşturursa manyetik dipolün manyetik indüksiyon alanı uygulanan dış manyetik indüksiyon alanın süperiletken küreden dışarıya itmektedir. Manyetik dipol momentinin oluşturduğu manyetik indüksiyon alanı B0 B0r Bd= p 0 m 2 1 3cos 3 4r olarak verilir. Radyal ve teğetsel yönde bileşenleri küre üzerindeki bir nokta için Bdr= 2 0p mcos ; Bdr= 0 pmsin 3 4r 3 4r olarak yazılabilir. Dışarıdaki manyetik indüksiyon alanın bileşenleri Br=Bcos; Br=Bsin olur. Süperiletken topun özelliği manyetik indüksiyon alanın yüzeye normal bileşenin sıfır olduğundan oluşan manyetik dipolün manyetik dipol momenti 3 Br=Bdr, 2 0p mcos =Bcos; B= 2 0pm ; pm= 2 r B 3 4r 3 4r 0 olarak bulunur. Bir manyetik dipol manyetik alana belli hız ile atılırsa manyetik alandan yansıyabilir. Yansıma şartını bulmak için gradienti olan manyetik indüksiyon alanlarda manyetik dipollere etki eden kuvvet ve yapılan işi bulmalıyız. Etki eden kuvvet F=pm dB dx bu kuvvetin dx yolunda yaptığı iş dA=Fdx=pmdB tüm iş kinetik enerjiye eşit ise A== mv 2 B 2r 3BdB r 3B2 = = 2 0 0 0 yansıma gerçekleşir. Buradan manyetik dipolün yansıması için şart 3 2 v 2 r B = m 0 olarak bulunur. 2r B 3 4 r 0 3 3 2 2 = 3B 20 Rafet Kamer, Fizik öğretmeni – Beyhan Rıfat Cıkılıoglu, Anadolu Lisesi, Eskişehir Manyetik dipolün oluşturduğu alan ile çok ilginç bir değerlendirme yapılabilir. Son verilere göre yapılan deneylerde elektronun yükü qe ve protonun yükü qp arasındaki fark qp q e qp 10-21 olarak ölçülmüştür. r Diğer taraftan ise dünyanın manyetik alanın doğası ile ortaya konulan çok net bir model yoktur. Yerin manyetik indüksiyon alanı B3.10-5 T q deneysel olarak bilinmektedir. Elektronlar ile protonlar arasındaki yüklerin arasında varsayılan yük farkı dünyanın manyetik alanın açıklaması mümkün olup olmadığı irdeleyebiliriz. Bunun için dünyada bulunan atomların atom kütlelerinin proton sayısına oranını A/Z2 kabul edebiliriz. Dünyanın yarıçapı 6378 km, kütlesi mD=6.1024 kg, bir nükleonun kütlesi 1,67.10-27, kg ve yükü e=1,6.10-19 C sayısal olarak da değerlendirme için gerekli olan bilgilerdir. Proton ve elektronun yüklerin muhtemel farklılığından kaynaklanan dünyanın toplam yükü q olsun. Bu yük sadece ve sadece yüklü parçacıkların yük farkından kaynaklanılabilir. Tüm parçacık sayısı N= M 6.1024 = =3,59.1051 27 m 1,67.10 proton sayısı Np= N =1,796.1051 2 ve teşkil ettikleri yük farkı q=Npq=1,796.1051.10-21.1,6.10-19=2,874.1011 C olur. r<R yarıçapında ve dr kalınlıkta küresel bir kabuk seçelim. Bu kabukta yarıçapı rsin bir halka seçelim. Bu halkanın hacmi dV=2rsin.rd.dr olur. Bu halkanın içindeki yük dq= qdV 2qr 2 sin drd = V V olur. Dönme sonucu seçilen halkanın oluşturduğu elektrik akım d= dq qr 2 sin drd = T V bu akımın oluşturduğu manyetik dipol momenti dpm=dS= qr 2 sin drd q r 4 sin 3 dr d (rsin)2= V V olur. Tüm kürenin dipol momenti R pm= 0 0 q r 4 sin 3 dr d qR 2 = V 5 = 2qR2 5T olarak bulunur. Bu manyetik dipol momentinin oluşturduğu manyetik indüksiyon alanı B= 20 pm 4R3 = 40 q 4.5RT = 4.107.3,14.2,874.1011 5.6378.103.24.3600 =1,3.10-7 T olarak bulunur. Görüldüğü gibi sonuç iki mertebe olarak daha küçüktür. Verilen farkı yerin manyetik indüksiyon alanın kaynağı olarak göstermek mümkün değildir. Manyetik dipollerle ilgili bir çok uygulama yapılabilir. Gösterilen yöntemler eğitimde öğrencilere belli ölçüde kolaylık ve aynı zamanda model kurma, matematiksel değerlendirme yapmaya yöneliktir. Yine de unutulmaması gereken öğrencilerin mutlaka yüksek matematik bilgisi sahibi olmaları gerçeğidir.









