Slide 1 - Ninova
advertisement
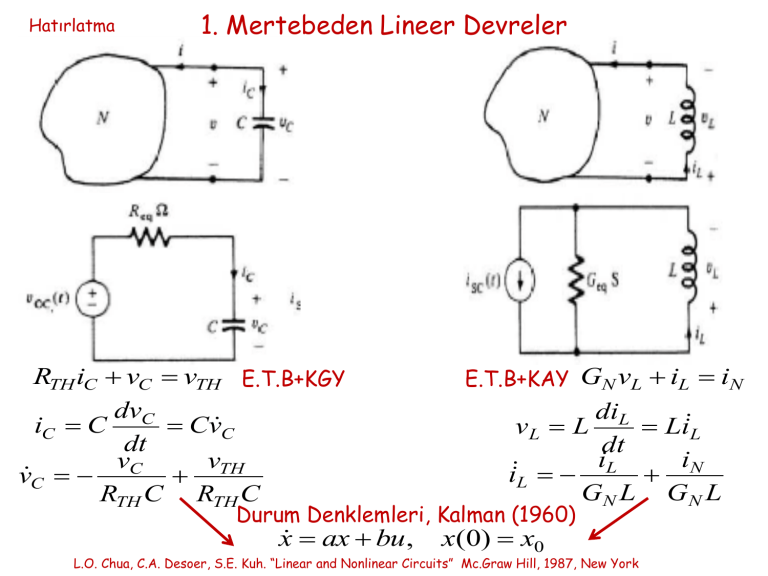
Hatırlatma 1. Mertebeden Lineer Devreler RTH iC vC vTH E.T.B+KGY dvC iC C CvC dt vC vTH vC RTH C RTH C E.T.B+KAY GN vL iL iN diL LiL dt i i iL L N GN L GN L vL L Durum Denklemleri, Kalman (1960) x ax bu, x(0) x0 L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York Hatırlatma 1. Mertebeden Diferansiyel Denklem Çözümü x ax dx ax dt x(0) x0 x (t ) C t dx adt x 0 Inx (t ) InC at x(t ) In at C x(t ) Ceat t x (0) Cea 0 x(t ) eat x0 x ax u x(0) x0 varsayım: x(t ) S (t )e at d ( S (t )e at ) a ( S (t )e at ) u(t) dt dS(t) at at aS (t )e e aS (t )e at u(t) dt t dS(t) at e u(t) dt dS(t) e atu(t) dt varsayım: x(t ) S (t )e at t S (t ) e a u()d S (0) 0 t x(t ) S (0)e at e a (t )u ( ) d , 0 0 0 x(0) S (0)e a 0 e a (t )u ( )d , 0 t x(t ) e at x(0) e a (t )u ( ) d 0 t x(t ) e at x(0) e a (t )u ( ) d öz çözüm 0 zorlanmış çözüm t t Durum Denkemlerinin Elde Edilmesi I- İki uçlu direnç, endüklenmiş kapasite bağımsız akım ve gerilim kaynaklarının oluşmuş devrelerde durum denklemlerinin elde edilmesi Amaç: x Ax Bu y Cx Du , x (0) x0 x Rn durum değişkenleri - kapasite gerilimleri, endüktans akımları y R r çıkış büyüklükleri - ilgilenilen eleman akımları ve gerilimleri u R p giriş büyüklükleri - bağımsız akım kaynağının akımı ve bağımsız gerilim kaynaklarının gerilimleri Yöntem: 1. Adım: Uygun Ağaç Seçimi a-) gerilim kaynaklarını dal elemanı olarak seçiniz, ağaç tamamlanmamışsa (b)’ye geçiniz b-) kapasiteleri dal elemanı olarak seçiniz, ağaç tamamlanmamışsa (c)’ye geçiniz c-) dirençleri dal elemanı olarak seçiniz, ağaç tamamlanmamışsa (d)’ye geçiniz c-) endüktansları dal elemanı olarak seçiniz 2. Adım: Durum değişkenlerini belirleme Dallardaki kapasite gerilimleri, kirişlerdeki endüktans akımları durum değişkenleridir. Durum değişkenlerini belirleyiniz ve uç denklemlerini yazınız. C dvc (t ) ic (t ) dt L 3. Adım: Durum denklemlerini yazma diL (t ) vL (t ) dt Lineer bağımsız akım denklemlerini yazınız (Temel kesitlemelere ilişkin denklemler) Lineer bağımsız gerilim denklemlerini yazınız (Temel çevrelere ilişkin denklemler) Yazdığınız denklemlerden yararlanarak dallardaki kapasitelerin akımları ile kirişlerdeki endüktansların gerilimlerini, durum değişkenleri ve girişler cinsinden belirleyiniz. Hangi devre büyüklüklerine karşı gelmekteler. II- Çok uçlu direnç, endüklenmiş kapasite bağımsız akım ve gerilim kaynaklarının oluşmuş devrelerde durum denklemlerinin elde edilmesi Yöntem: 1. Adım: Uygun Ağaç Seçimi Bir önceki durumdaki adımlar atılmadan önce • Devrede bulunan çok uçluların yazılabilen tüm uç denklemlerini gözönüne alınız • Her bir denklem için gerilim büyüklüğüne karşı gelen ucu grafa dal olarak , akım büyüklüğüne karşı gelen ucu grafa kiriş elemanı olarak yerleştiriniz. Bir önceki durumdaki adımları izleyerek ağacı belirleyiniz. Farklı uç denklemlerinden hangisi daha fazla durum değişkeni veriyorsa o duruma ilişkin ağacı uygun ağaç olarak seçiniz. Diğer Adımlar: devrede 2-uçlu direnç elemanı, kapasite, endüktans ve bağımsız kaynaklar varken ki durum ile aynı 2. Mertebeden Diferansiyel Denklemlerin Çözümü x1 a11 x a 2 21 a12 x1 b1 u , a22 x2 b2 x Ax Bu , x(t0 ) x0 x(t0 ) x0 Çözüm, 1. mertebeden diferansiyel denklemlerin çözümlerine benzer şekilde x (t ) x (t ) x (t ) T h özel Homojen kısım: x Ax, xh (t ) Set x(t0 ) x0 S1 t e S2 Set ASet S AS I AS 0 detI A 0 Çözüm Tahmini belirlememiz gereken kaç büyüklük var? sıfırdan farklı çözüm erin olması nasıl mümkün olur? 2 a b 0 Karakteristik Denklem Karakteristik denklemin kökleri: 1, 2 özdeğerler Belirlememiz gereken S özvektör Hangi uzayın elemanı? O uzaya ait neyi belirlersek aradığımızı bulmuş oluruz? 1I AS1 0 1‘e ilişkin özvektör 2 I AS2 0 2‘e ilişkin özvektör S1 c1V1 S2 c2V2 1t xh (t ) e V1 c1 c1 e V2 M (t ) c2 c2 2t M (t ) Özel çözüm: x1ö zel (t ) xözel (t ) x ( t ) 2ö zel Tam çözüm: Temel Matris Nasıl belirleyeceğiz? x(t ) M (t )C xözel (t ) C M (t0 )1x(t0 ) xözel (t0 ) x(t ) M (t )M 1(t0 )x(t0 ) xözel (t0 ) xözel (t ) x(t0 ) M (t0 )C xözel (t0 ) x(t ) M (t )M 1(t0 )x(t0 ) xözel (t0 ) xözel (t ) (t ) Durum Geçiş Matrisi x(t ) (t ) x(t0 ) xözel (t ) (t ) xözel (t0 ) x(t ) (t ) x(t0 ) xözel (t ) (t ) xözel (t0 ) öz çözüm zorlanmış çözüm t x(t ) e At x(t0 ) e A(t ) Bu ( )d öz çözüm t0 zorlanmış çözüm