BOYUTSUZ SAYILAR VE FİZİKSEL ANLAMLARI Naci Kalkan Bitlis

BOYUTSUZ SAYILAR VE FİZİKSEL ANLAMLARI
Naci Kalkan
Bitlis Eren Üniversitesi
Mühendislik Mimarlık Fakültesi
Makina Mühendisliği Bölümü – Enerji Ana Bilim Dalı
Bitlis – Türkiye
nkalkan@beu.edu.tr
Giriş - Boyutsuz Sayılar
Isı transferi ve akışkanlar mekaniğinde bazı temel denklemler çok karmaşık olup çoğunun
çözümü sayısal yöntemlerle dahi zordur. Karmaşıklığa yol açan terimler akım alanının bazı
bölgelerindeki fiziksel büyüklükler korunmak şartıyla ihmal edilirse bir takım basitleştirmeler
ortaya çıkar ve bu denklemler daha kolay çözülebilir. Diferansiyel denklemlerdeki çeşitli
terimlerin oransal büyüklüklerini belirlemek için boyut analizinden faydalanılır [1]. Örnek
olarak sabit viskoziteli ve sabit yoğunluklu akışkan halini ele alalım. Akışı yöneten
denklemleri şu şekilde yazabiliriz.
(1)
(2)
Tablo 1- Akışa ait referans büyüklükler, [1].
L
Referans uzunluk (kanat veter uzunluğu)
V
Referans hız (serbest akım hızı)
T
Karakteristik zaman (periyodik olaylarda bir çevrimin süresi veya, L/V)
Referans basınç (serbest akım basıncı,
)
Bünye kuvveti (yer çekim ivmesi, )
Naci Kalkan
Bu tanımlamalar ile kartezyen koordinatlarda aşağıdaki boyutsuz büyüklükler elde edilebilir:
(3)
Karakteristik
büyüklükler uygun biçimde alınırsa bütün bu boyutsuz büyüklükler 1
mertebesinde olur.
Şimdi bu boyutsuz büyüklükleri akışı yöneten denklemlerde kullanalım. Süreklilik denklemi
için aşağıdaki denklem elde edilir.
(4)
Diğer terimler için de benzer işlemler uygulanırsa, sıkıştırılamaz akışa ait süreklilik denklemi
şu şekle dönüşür:
(5)
Momentum denkleminin x doğrusundaki bileşeni için benzer işlemler uygulanırsa aşağıdaki
denklem elde edilir:
(6)
Naci Kalkan
Momentum denkleminin diğer bileşenleri için de benzer ifadeler elde edilebilir. (5) denklemi
(L/V) ile ve (6) denklemi de (L/
) ile çarpılarak (7) ve (8) denklemleri elde edilir [1].
(7)
(8)
Eğer (4) denklemindeki bütün boyutsuz büyüklükler 1 mertebesinde ise denklemler (7) ve
(8)’deki her bir terimdeki yıldız indisli büyüklüklerin oluşturduğu gruplar da 1 mertebesinde
olacaktır. Bu durumda denklemlerdeki her bir terimin büyüklük mertebesini, bu terimlerin
başında parantezler içinde yer alan ve yıldız indisine sahip olmayan çarpanlar belirleyecektir.
Parantez içerisindeki bu büyüklüklerin teşkil ettikleri grupların boyutsuz oldukları
görülmektedir.
Süreklilik denkleminde parantez içerisinde, yukarıda belirtildiği gibi büyüklükler olmayıp,
herhangi bir üç-boyutlu akış için bu denklemin her bir terimi aynı mertebede ve aynı öneme
sahiptir.
Momentum denklemindeki boyutsuz büyüklükler
Strouhal Sayısı:
Momentum denkleminin sol tarafındaki ilk terimin başındaki parantez içinde kalan büyüklük
ele alınan akımda zamana bağlılığın hangi mertebede olduğunu belirten bir boyutsuz sayı
teşkil etmektedir.
(9)
Naci Kalkan
Bu boyutsuz sayının pratikte daha sık kullanılan bir şekli, periyodik olayın frekansının tersi
karakteristik zaman olarak alınarak tanımlanan Strouhal sayısıdır. Eğer Strouhal sayısı çok
küçük ise (8) denkleminin ilk terimi 1 mertebesindeki diğer terimler yanında ihmal edilebilir.
(10)
Froude Sayısı:
Momentum denkleminin sağındaki ilk terimde çarpan olarak parantez içinde yer alan
büyüklükler, bünye kuvvetinin, örneğin, yerçekimi kuvveti olarak alınması (f0 olarak g
yerçekimi ivmesinin alınması) halinde yine boyutsuz bir büyüklük teşkil ederler. Bu boyutsuz
büyüklük, Froude sayısı olarak tanımlanan bir sayının tersinin karesine eşittir [1].
(11)
Froude sayısı atalet kuvvetlerinin yerçekimi kuvvetlerine oranı olarak da tanımlanabilir.
Froude sayısının küçük olması, ele alınan problem için bünyesel kuvvetin önemli olduğu ve
buna ilişkin terimin denklemde yer alması gerektiği anlamına gelir,[1]. Serbest yüzeyli akarsu
akışları, şelale akımları, gemi hidrodinamiği gibi problemler bu duruma örnek olarak
gösterilebilir.
Euler sayısı:
Momentum denkleminde yer alan üçüncü boyutsuz sayıdır. Basınçla atalet kuvvetlerinin
oranını belirtir.
(12)
Naci Kalkan
Pratikte bu sayı yerine genellikle basınç katsayısı kullanılır:
(13)
Reynolds sayısı :
Reynolds sayısı ısı transferi ve akışkanlar mekaniği için çok önemli bir boyutsuz sayıdır [2]. Şu
şekilde gösterilebilir:
Levha
Silindir, Küre
Momentum denklemindeki sonuncu boyutsuz grup atalet kuvvetlerinin viskozite
kuvvetlerine oranını belirten sayıdır.
(14)
Buradaki
büyüklüğü kinematik viskozitedir. Gaz akışları için kinetik teori yaklaşımıyla
viskozite, molekullerin c karakteristik hızlarına ve
ortalama serbest yörüngelerine
bağlanabilir[3].
Buradan yola çıkarak Reynolds sayısının (hız x uzunluk ) büyüklüğünün moleküler ölçekle
kıyaslamasını yaptığı anlaşılır.
Naci Kalkan
( )( )
Not: Bu bölümdeki boyut analizi kolaylık sağlaması açısından sıkıştırılamaz akışlar için
yapılmıştır. Eğer sıkıştırılabilirlik dikkate alınırsa akım hızının ses hızına oranını belirten Mach
boyutsuz sayısı da yer alır. Euler sayısı Mach sayısı ile ilişkilendirilebilir (
Eğer
).
ise basınç değişikliklerinin oluşturduğu
yoğunluk değişimleri ihmal edilebilir ki, bu şartlarda akışkan sıkıştırılamaz olarak kabul edilir
[4].
Akış alanının uçaklarda, roketlerde ve dünya yüzeyinde olduğu durumlara dış akışlar, akış
alanının boru akışında olduğu gibi sınırlarla kuşatıldığı durumlara da iç akışlar denir. Yüzeye
yakın kısımlarda sürtünme kuvvetlerinin egemen olduğu ve yüksek hız gradyanlarının
görüldüğü bölgelere sınır tabaka denir. Yüzeyden uzak kısımlarda, serbest akış alanında
atalet kuvvetleri baskındır. Bu nedenle akış, hız ya da kuvvetler arasındaki orana göre
sınıflandırılır. Atalet kuvvetlerinin viskoz kuvvetlere oranına Reynolds sayısı denir ve Re ile
gösterilir. Reynold sayısı adını 1842 ile 1912 yılları arasında yaşamış olan ve bu sayıyı
tanımlayan Osborne Reynolds’tan almıştır [5]. Reynolds sayısı; akışkanın laminer (düzgün
akış çizgileri) ve türbülanslı (karmaşık, dalgalanmalı, tedirgin akış alanı) olduğunu
tanımlamada kullanılan en basit ve en yaygın boyutsuz sayıdır [6]. Reynolds sayısı dış akışlar
için:
şeklinde ifade edilir.
Burada V üst akım hızı,
geometrinin karakteristik uzunluğu ve
akışkanın kinematik
viskozitesidir.
Yüksek Reynolds sayılarında akışkanın özgül kütlesi ve hızı ile doğru olan atalet kuvvetleri,
viskoz kuvvetlere oranla daha büyüktür. Bu yüzden visoz kuvvetler, akışkanın gelişigüzel ve
Naci Kalkan
hızlı çalkalanmalırını engelleyemez. Fakat düşük ve orta Reynolds sayılarında viskoz
kuvvetler, bu çalkalanmaları bastırmak ve akışkanı hizada tutmak için yeterince büyüktür.
Böylelikle akış ilk durumda türbülanslı ikinci durumda ise laminardır.
Akışın türbülanslı hale geldiği Reynolds sayısı kritik Reynolds sayısı olarak adlandırılır. Kritik
Reynolds sayısının değeri farklı geometriler ve akış şartlarına göre faklılık gösterir. Düz bir
plaka üzerindeki akış için genel kabul gören kritik Reynolds sayısı
tir. Burada
plakanın ön kenarından itibaren , akışta laminardan türbülansa geçişin
olduğu, uzaklıktır [7].
Yüksek Reynolds Sayısındaki Akış:
Akışı yöneten denklemleri boyutsuzlaştırmanın en önemli yararı denklemlerde görünen
terimlerin oransal büyüklüklerinin belirlenmesi ve birbirleriyle karşılaştırılabilmesidir.
Böylece, istenirse küçük terimler ihmal edilebilir, ve kalan terimler daha kolay çözülebilir.
Ayrıca akışta hakim olan fiziksel büyüklükler de göz önüne alınmış olur. Sıkıştırılamaz haldeki
süreklilik denkleminde bütün terimler aynı büyüklük mertebesinde olup hiç birisi ihmal
edilmemiştir.
Momentum denklemine gelince, (8-14) eşitlikleri kullanılarak x doğrultusundaki bileşen için
boyutsuz sayılarla denklem (15) yazılabilir.
(15)
Şimdi bazı tipik mühendislik problemlerinde Reynolds ve Mach sayısı aralıklarını gözden
geçirelim. Pratikte mühendislik problemlerinin geniş bir kesiminde, uçak aerodinamiği, deniz
Naci Kalkan
araçlarının hidrodinamiği, Reynolds sayısı çok büyüktür (Şekil 1). Bunun sebebi ise have ve su
gibi tipik akışkanların viskozitesinin küçük olmasıdır.
Şekil 1- Bazı tipik akışkanlar için Reynolds ve Mach sayısı aralıkları, [1]
(15) denklemındeki viskoz terimlerin 1 mertebesindeki diğer terimlerden küçük olması
Reynolds sayısının çok büyük olduğu bir durumu gösterir. Bu terimler ihmal edilmeden önce
yüksek Reynolds sayılı akış şartlarına bakalım.
Şekil 2’ de görülen kanat profili etrafındaki akımda iki bölge vardır:
i.
Viskoz etkilerinin hakim olduğu sınır tabaka ve iz bölgesi
ii.
Viskoz etkilerin küçük olduğu dış bölge
Naci Kalkan
Şekil 2- Yüksek Reynolds sayısında kanat profile etrafındaki akış alanı, [1]
Dış Akım Bölgesinde:
Aşağıda belirtilen (16) denklemi birinci dereceden bir kısmi türevli diferansiyel denklem
olup, budenklem için katı cidar üzerinde bir tek hız bileşeni cinsinden sınır şartı yeterli
olmaktadır.
(Euler denklemi) (16)
Akım viskozitesiz kabul edildiğinden durağan katı cidar üzerinde teğetsel hızın sıfır olmasının
bir anlamı olmayıp, sınır şartı olarak dikey hız bileşeninin sıfır olması yeterlidir:
(katı cidar üzerinde)
Sınır Tabaka ve İz Bölgesinde:
türevleri çok büyük olup, yüksek Reynolds sayılarında dahi viskoz terimler ihmal
edilemez. Bu durumda katı cidarın yakın civarındaki bu bölge içerisinde Navier-Stokes
denklemleri klasik sýnýr-tabaka denklemlerine indirgenir, [8]:
Naci Kalkan
(17)
(18)
Sonuç :
Yüksek Reynolds sayılarında akım alanında iki hakim bölge bulunmaktadır:
i.
Katı cidarın uzağında, viskoz etkilerin ihmal edildiği dış akım bölgesi: Bu bölgede
viskoz olmayan akım çözümü basınç dağılımını ve buna bağlı kuvvetleri verir.
ii.
Katı cidarın yakın civarında, viskoz etkilerin ihmal edilemediği ince sınır-tabaka
bölgesi: Bu bölgede sınır-tabaka denklemlerinin çözümü kayma-gerilmeleri ve buna
bağlı (sürtünme) kuvvetlerini verir.
Sınır tabaka denklemlerinin çözümünde, katı cidar üzerinde kaymama sınır şartı uygulanır.
Sınır tabaka içerisindeki teğetsel hız dağılımı Şekil 2 ‘de verildiği gibi olup, dış akım bölgesine
yaklaştıkça teğetsel hızın z ile değişmediği görülmektedir. Sınır tabaka ile dış akım bölgesinin
girişim yeri kesin şekilde belirlenememekle birlikte katı cidardan, sınır tabaka kalınlığı olarak
adlandırılan bir
mesafesinde olduğu ifade edilir. Yüksek Reynolds sayısında sınır tabaka
kalınlığının cismin karakteristik uzunluğuna (örneğin bir kanat profili için veter uzunluğu)
bölümünün
√
ile orantılı olduğu bilinir [8].
Naci Kalkan
Prandtl Sayısı :
Hız ve ısıl tabakaların birbirlerine göre kalınlıklarını en iyi tanımlayan boyutsuz parametre
olan Prandtl sayısıdır.
Prandtl sayısı viskozite ve ısıl iletkenlik katsayıları yanında sabit bsınçta özgül ısı katsayısı cp ’
ye bağlı olarak tanımlanabilir. Bu bağıntı da,
şeklinde düzenlenirse momentum yayınım (difüzyon) katsayısı ile ısı yayınım katsayısı oranını
temsil ettiği görülür. Akışkanların Prandtl sayıları sıvı metaller için 0.01’in altından, ağır
yağlar için 100,000’ in üstündeki değerlere kadar değişir. Suyun Prandtl sayısının 10
mertebesinde olduğuna dikkat edilmelidir.
Gazların Prandtl sayıları ise 1 civarındadır. Bu değer ise akışkan içinde momentum ve ısı
yayınımın aynı hızda olduğunu gösterir.Isı momentuma göre sıvı metallerde (Pr <<1) çok
hızlı, ağır yağlarda (Pr>>1) çok yavaş yayılır. Sonuç olarak ısıl sınır tabaka hız sınır tabakasına
göre sıvı metallerdeçok daha kalın, yağlarda çok daha incedir [7,9].
Nusselt Sayısı :
Bu parametre, yüzeydeki boyutsuz sıcaklık gradyanına eşittir ve yüzeyde oluşan taşınımla ısı
geçişinin bir ölçüsünü verir [10].
Naci Kalkan
Burada
akışkanın ısıl iletkenliği ve
karakteristik uzunluktur. Akışkan tabakasındaki ısı
transferi, akışkan bir miktar hareket içerdiği zaman taşınımla, akışkan tabakası hareketsiz
olduğu zaman iletimle olur. Her iki durumdaki ısı akısı (birim alan başına düşen transfer hızı),
̇ taşınım =h
ve
̇ iletim =k
şeklindedir. Bu ifadelerin oranı:
̇
̇
ifadesini verir ki bu da Nusselt sayısıdır.Dolayısıyla Nusselt sayısı, bir akışkan tabakası
üzerinde taşınımın iletime oranının sonucu olarak, o akışkan tabakasındaki ısı transferi
iyileşmesini gösterir. Nusselt sayısı ne kadar büyük olursa taşınımda o kadar etkili olur.
Sherwood Sayısı:
Burada L karakteristik uzunluk,
kütle yayınımı ve
kütle transfer katsayısıdır.
Bu parametre, yüzeydeki boyutsuz derişiklik gradyanına eşittir ve yüzeyde gerçekleşen
taşınımla kütle geçişinin bir ölçüsüdür. Nusselt sayısının ısıl sınır tabakada gördüğü işlevi
Sherwood sayısı, derişiklik sınır tabakasında görür [11].
Peclet:
Prandtl sayıları çok küçük olan akışkanlar, başka bir değişle, sıvı metaller için Peclet sayısından
yararlanılır. Bununla beraber, bu durum için ısıl sınır tabakanın oluşumu hız sınır tabakanın
Naci Kalkan
oluşumundan daha hızlıdır. Isıl sınır tabaka boyunca hız sabit kabul edilir. Bu varsyıma dayanarak ısıl
sınır tabaka denkleminin bir çözümünden aşağıdaki denklem elde edilir.
Stanton sayısı:
Not: Denklemlerde akışkana ait özellikler tablolardan seçilirken akışkan-yüzey ortalama sıcaklığı
değeri göz önüne alınız:
Boyutsuz Parametrelerin Fiziksel Anlamı
Yukarıdaki adı geçen tüm boyutsuz parametrelerin sınır tabakalarındaki koşullara bağlı
fiziksel yorumları vardır. Hız sınır tabakası içinde atalet kuvvetlernin sürtünme kuvvetlerine
oranı olarak da yorumlanabilen Reynold sayısını, Re, göz önüne alalım. Bu sınır tabakan
içindeki bir diferansiyel kontrol hacmi için atalet kuvvetleri, akışkan kontrol hacminden
geçerken momentum akısındaki değişim ile ilişkilidir. Atalet kuvvetleri yaklaşık olarak
olur. Benzer biçimde, net kayma kuvveti
Benzer biçimde, net kayma kuvveti
[ (
)]
ile gösterilmektedir.
olur. Böylece kuvvetlerin oranı,
sayısını verir. Bu nedenle atalet kuvvetlerinin Re sayısının büyük değerleri için, sürtünme
kuvvetlerinin ise Re’ nin küçük değerleri için etkin olduklarını düşünürüz.
Naci Kalkan
Bu sonucun dolaylı yoldan birçok önemli bağlantısı vardır. Anımsanırsa Reynold sayısı, akışın
laminar veya türbülanslı olduğunu belirtir. Herhangi bir akışta küçük çalkantılar büyüyerek
türbülanslı koşulları oluşturabilir. Ama, Re’nin küçük değerlerinde sürtünme kuvvetleri,
atalet kuvvetlerine gore yeterince büyüktür ve laminar akış korunur. Ancak, Re’nin artan
değerleri ile, sürtünme kuvvetleri atalet kuvvetleri yanında küçük kalır ve küçük çalkantılar
büyüyerek türbülansa geçişi sağlar. Bunun yanısıra Reynolds sayısının büyüklüğünün, hız
sınır tabakasının kalınlığını etkilediği vurgulanmalıdır. Re’nin yüzeydeki belirli bir bölgede
artışı ile sürtünme kuvvetlerinin atalet kuvvetlerine gore önemi azalır ve sürtünmenin
serbest akış etkisi, başka bir değişle değeri küçülür.
Prandtl sayısının fiziksel yorumu,
momentum yayılımının,
ısı ıletimine oranı şeklinde
yapılabilir. Prandtl sayısı, hız ve ısıl sınır tabakalar içinde yayılımla momentum ve enerji
aktarımının birbirlerine oranını gösterir. Daha önce gazların Prandtl sayısının bire yakın, sıvı
metallerde Pr<<1 ve yağlarda Pr>>1 olduğunu daha önce belirtmiştik. Bu yorumdan, Pr
sayısının, hız ve ısıl sınır tabakalarının bağıl büyümesini önemli ölçüde etkilediği söylenebilir.
Aslında laminer sınır tabakalarında (türbülanslı karışımın olmadığı yayılımda) su sonuç
beklenebilir:
Burada n artı değerde bir üsttür. Böylece gazlar için
için ise
, sıvı metaller için
, yağlar
olur.
Benzer biçimde Schmodt sayısı da , hız ve derişiklik sınır tabakalarında yayılımla momentum
ve kütle aktarımın birbirlerine oranıdır. Böylece Laminar akışlardaki taşınımla kütle geçişi için
sayısı hız ve derişiklik sınır tabakalarının kalınlıklarının birbirlerine oranını belirtir.
Pr ve Sc ile bağlantılı bir başka parametre de Lewis sayısıdır (Le). Bu sayı şöyle tanımlanır:
Naci Kalkan
Taşınım ile ısı ve kütle geçişinin birararada gerçekleştiği durumlarla ilgilidir.
Böylece Lewis sayısı, ısı ve derinlik sınır tabakalarının kalınlıklarının oranı ile ilişkilidir.
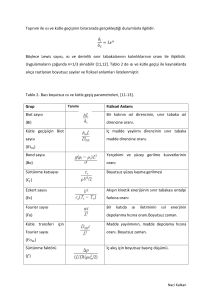
Uygulamaların çoğunda n=1/3 alınabilir [11,12]. Tablo 2 de ısı ve kütle geçişi ile kaynaklarda
sıkça rastlanan boyutsuz sayılar ve fiziksel anlamları listelenmiştir.
Tablo 2- Bazı boyutsuz ısı ve kütle geçiş parametreleri, [11-13].
Tanımı
Grup
Fiziksel Anlamı
Biot sayısı
Bir katının ısıl direncinin, sınır tabaka ısıl
(Bi)
direncine oranı.
Kütle geçişiiçin Biot
İç madde yayılımı direncinin sınır tabaka
sayısı
madde direncine oranı.
(
)
Bond sayısı
Yerçekimi ve yüzey gerilme kuvvetlerinin
(Bo)
oranı
Sürtünme katsayısı
Boyutsuz yüzey kayma gerilmesi
( )
Eckert sayısı
Akışın kinetik enerjisinin sınır tabakası entalpi
(Ec)
farkına oranı
Fourier sayısı
Bir
(Fo)
depolanma hızına oranı.Boyutsuz zaman.
Kütle transferi için
Madde yayılımının, madde depolama hızına
Fourier sayısı
oranı. Boyutsuz zaman.
(
katıda
ısı
iletiminin
ısıl
enerjinin
)
Sürtünme faktörü
İç akış için boyutsuz basınç düşümü.
( )
Naci Kalkan
Grashof sayısı
Kaldırma
(
kuvvetlerine oranı.
)
Colburn j faktörü
(
kuvvetlerinin,
sürtünme
Boyutsuz ısı geçiş katsayısı.
)
Colburn j faktörü
(
Boyutsuz kütle geçiş katsayısı
)
Jakob sayısı
Duyulur
ısının,
sıvı-buhar
faz
değişimi
(Ja)
sırasında gizli ısıya oranı.
Lewis sayısı
Isı ve kütle yayılım katsayılarının oranı.
(Le)
Nusselt sayısı
(
Yüzeydeki boyutsuz sıcaklık gradyanı.
)
Peclet sayısı
(
)
Prandtl sayısı
Boyutsuz bit ısı geçişi parametresi
Momentum ve ısı yayılım katsayılarının oranı.
(Pr)
Reynolds sayısı
(
Atalet ve sürtünme kuvvetlerinin oranı
)
Schmidt sayısı
Momentum ve kütle yayılım katsayılarının
(Sc)
oranı.
Sherwood sayısı
Yüzeydeki boyutsuz değişiklik gradyanı
(
)
Stanton sayısı
Değiştirilmiş Nusselt sayısı
(St)
Kütle transferi için
Değiştirilmiş Sherwood sayısı
Stanton sayısı
(
)
Weber sayısı
Atalet ve yüzey gerilme kuvvetlerinin oranı
(We)
Naci Kalkan
Rayleigh sayısı
Pr >> 1 olan doğal akışlar için
(Ra)
Boussinesq sayısı
Pr << 1 olan doğal akışlar için
(Bo)
Euler Sayısı
Orifis içi akış için boyutsuz basınç düşümü
(Eu)
References
1. Yükselen, M.A. Hesaplamalı Aerodinamik ders notları,
“web.itu.edu.tr/~yukselen/UCK419/UCK419_Index.html ”, Erişim tarihi 29 Mart 2014.
2. Maliska, C. R. (1990). On the Physical Significance of Some Dimensionless Numbers Used in
Heat Transfer and Fluid Flow. Federal University of Santa Catarina, Florianópolis, SC.
3. Yuan S.W., Foundation of Fluid Mechanics, 1969, sayfa 257
4. Peremeci, Ö.E, Akışkan hareketinde temel ilkeler, “www.peremeci.org/wp
content ploads 2010 04 akm2.doc”, Erişim tarihi 25 Mart 2014.
5. Reynolds sayısı ve fiziksel anlamı, “http://www.kisa-ozet.net/reynolds-sayisi-nedir-fizikselanlami/” , Erişim tarihi 27 Mart 2014.
6. Akışkanlar mekaniği, Sürtünmeli akışlar, http://www.fizikevreni.com/akiskanlarmekanigi.pdf”,
Erişim tarihi 24 Mart 2014
7. Çengel, Y. "Isı ve kütle transferi pratik bir yaklaşım (Translation from 3. edition)." (2011),
Tanyıldızı V. , Dağtekin İ.
8. (Schlichting H., Boundary layer theory, McGraw-Hill, 1979, sayfa 129).
9. Cengel, Y. A., & Cengel, Y. (2003). Heat Transfer A Practical Approach with EES
CD. McGraw Hill Professional.
10. Taşınım ile ısı transferi,
“http://eng.harran.edu.tr/moodle/moodledata/20/Yesilata/Ders_Notlari/3HeatT_ch3_pg79109.pdf”, Erişim tarihi 27 Mart 2014.
11. Incropera, F. P., & DeWitt, D. P. (2007). Isı ve kütle geçişinin temelleri. Literatür Yayıncılık.
12. Incropera, F. P., Lavine, A. S., & DeWitt, D. P. (2011). Fundamentals of heat and mass
transfer. John Wiley & Sons.
13. Mills AF, Heat Transfer, Second Edition, ISBN 0-13-947624-5, Pretice Hall, NJ.
Naci Kalkan