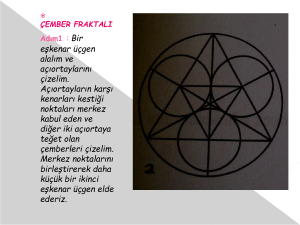
Dönme Simetrisi Öğretimi Üzerine
Abdulkadir ÖRNEKÇİ*
Bir şeklin veya geometrik cismin ekseni etrafında 3600 den daha küçük bir açı
kadar dönmesi neticesinde eski halini alabiliyor olması durumu dönme simetrisi olarak
adlandırılır.
En Küçük Dönme Simetrisi Açısı:
Bir şeklin veya cismin eski halini alabilmesi için dönmesi gereken en küçük açıya
“en küçük dönme simetrisi açısı” (EKDSA) adı verilir. Dönme simetrisine sahip olan bir
şekil veya cisim EKDSA ve o açının katları kadar açı ile döndürüldüğünde eski halini
alır. Ayrıca dönme simetrisinde saat yönünde ya da saatin tersi yönde dönülmesinin
bir önemi yoktur. Örneğin bir kare, ekseni etrafında en az 900 lik bir açı ile
döndürüldüğünde eski halini alır. Yani, kareye ait EKDSA 900 dir. Bir öğretmen olarak
derste elime kare şeklinde bir nesne alıp düz bir zemin üzerine koyup;
“En az kaç derecelik bir açı ile döndürürsem bu şekil yineeski halini alır?”
Şeklinde bir soru sorduğumda aldığım cevap 900 oluyor.Bunu öğrenciler sezgileri
ve yaşantıları yardımıyla bilebiliyorlar. İlk şekil olarak kareyi seçmemin esas sebebi de
bu. Öğrencilerin çokça kullandıkları, tanıdıkları bir şekli seçerek, verecekleri doğru
cevap sayesinde başarı hazzını yaşamalarını sağlamak. EKDSA geometrik cisimlerden
dik prizmalar ve dik piramitler için söz konusu olduğunda tabanlarında bulunan
çokgenin ne olduğu önemlidir.Örneğin kare dik piramidin tabanında kare olduğundan
kare dik piramide ait EKDSA kareninki ile aynı ve 900 dir.Buraya kadar her şey
yolunda gidiyor ancak eşkenar üçgene ait EKDSA‟yı sorduğumda aldığım cevap
genellikle 600 oluyor. Bu yanılgının üstesinden gelmek için gerçek yaşam durumlarına
müracaat ederek şekiller çiziyorum.
*
1
Matematik Öğretmeni, Toplu Konut Ortaokulu / ERZURUM
Cin Ali‟nin 1. şekildeki eşkenar üçgeni ip bağlayarak çekmesi ve 2.durumdaki
hale getirmesi ancak 1200 lik bir dönme ile mümkün olabilecektir. Görüldüğü üzere
eşkenar üçgenin bir dış açısının ölçüsü 1200 dir.
Şimdi, bu durumu düzgün çokgenler için genelleştirme ve ayrıntıları ile daha
kalıcı hale getirme zamanı.
Düzgün çokgen biçimindeki bir şekli eski hali ile çakıştırmak (ilk haline
getirmek) için en azından bir dış açısı kadar kendi ekseni etrafında döndürmek
gereklidir.
“n” kenarlı
bir düzgün çokgenin bir dış açısının ölçüsü( 360/n)0 bağıntısı ile
bulunur.
Tablo 1. Geometik şekil ve cisimlerin en küçük dönme simetri açıları
Şekil veya cisim
EKDSA
Eşkenar üçgen, eşkenar üçgen dik prizma, eşkenar üçgen dik piramit
1200
Kare, kare dik prizma ve kare dik piramit
900
Düzgün beşgen, düzgün beşgen dik prizma, düzgün beşgen dik piramit
720
Düzgün altıgen, düzgün altıgen dik prizma, düzgün altıgen dik piramit
600
“Düzgün n gen”, “düzgün n gen dik prizma”, “düzgün n gen dik piramit”
( 360/n)0
Tablo.1 de görüldüğü üzere bir düzgün çokgenin en küçük dönme simetrisi açısı
kenar (veya köşe) sayısı ile ters orantılıdır.
Bu durumu öğrencilere açarken köşe kapmaca oynayan çocukları örnek
gösteriyorum. Çocuk sayısı ne kadar çok ise bir çocuğun, diğer arkadaşının boş
bıraktığı köşeyi kapma için göstereceği çaba azalır. Çünkü köşeler birbirine o kadar
yakındır.
Düşündürücü soru: Çocuk sayısını daha da artırırsak koşmamız gereken mesafe
hakkında ne söyleyebilirsiniz?
Bu noktada hayal gücünden yardım alarak bir örnek daha verilebilir.Kare
şeklindeki tekerleklere sahip olan araçlarla oldukça sarsıntılı bir yolculuk yapılacağı,
tekerleğin şekli düzgün beşgen, ardından düzgün altıgen olursa sarsıntının sürekli
azalacağı vurgulanır.Nihayetinde ise tekerleğin daireye dönüşmesi sonucunda
sarsıntısız bir yolculuk yapılacağı sınıfça (yeniden) keşfedilir.
“Dairenin içine çizilen düzgün çokgenin köşe sayısı sonsuza yaklaşırsa köşeler
arasındaki uzaklık sıfıra yaklaşır” cümlesini ortaokuldan başlayarak tüm sınıf
düzeylerinde kullanabiliriz sanırım.
Zaten az önce köşe sayısı ile EKDSA arasında ters bir ilişki olduğunu
vurgulamıştık.
EKDSA= 360/n idi. Burada “n” sonsuza yaklaşırsa EKDSA da 0
(sıfır)‟a yaklaşır.Bu durumda çokgenlerden daireye ve tabanı daire olan dik koni ve dik
silindire de geçiş yapılabilir.
Düzgün Olmayan Çokgenler: Düzgün çokgenleri, tabanı düzgün çokgen olan dik
prizmaları ve dik piramitleri anlattıktan sonra daireyi ve tabanı daire olan dik koni ve
dik silindiri de anlatabildiğimi zannediyorum. Düzgün olmayan çokgenlerden
dikdörtgeni “Yukarıdaki kurallara uymamakla birlikte en az 180 lik bir açıyla ekseni
etrafında döndürürsek kendisi ile çakışır” şeklinde tarif edebiliriz.Bu hususta bir
genelleme amaçlı bir yaklaşım var ki o da 360‟ı eşit kenar sayısına bölmek şeklindedir.
3
Bu yaklaşım dikdörtgende tevafuk bulsa da (360/2=180), diğer çokgenlere genellemek
mümkün değildir. Örneğin ikizkenar üçgen dönme simetrisine sahip değildir. Yani
kendisi ile çakışması için (en az) tam bir tur döndürmek gereklidir. Bu durum 360/eşit
kenar sayısı yaklaşımına uymamaktadır.Dolayısıyla düzgün olmayan her şekli kendi
yapısı kapsamında ele almak daha doğru olacaktır.