batman anadolu lisesinin ortaokullara yönelik
advertisement

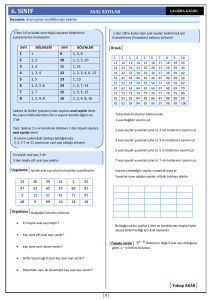
BATMAN ANADOLU LİSESİNİN ORTAOKULLARA YÖNELİK YAPACAĞI HAYAT MATEMATİK YARIŞMASI İÇİN ÖRNEK SORULAR 1. Aşağıdaki şekilde A noktasında bulunan bir kişi, çizgiler üstünde hareket ederek ve geçilen bir noktadan tekrar geçilmemesi şartıyla B noktasına yürüyecektir. Bu kişi kaç farklı yol takip edebilir? B A 2. ABCDE düzgün beşgeninde A noktasından CD doğrusuna inen dikme ayağı F, B noktasından DE doğrusuna inen dikme ayağı G olsun. AF ile BG nin kesişim noktası H dir. Alan( ABH ) x ise, x=? Alan( FDGH ) 3. x, y, z asal sayılar ve z x3 2 x 2 y 2 xy 2 y 3 ise, z nin alabileceği kaç farklı değer vardır? 4. CAB ve EFD eş üçgenlerdir. AC x y z , DF 2 y z , DE y 2 olduğuna göre x y z 3 a) 36 b) 40 c) 48 3 BC x 8 z , 3 AB z 6 , EF 3 , toplamının değeri kaçtır? d) 57 e) Hiçbiri 5. (k 1) (k 2) (k 3) ... (k 19) toplamının bir tam kare olmasını sağlayan en küçük iki k pozitif tamsayı değerinin toplamı kaçtır? a) 75 b) 66 c) 59 d) 48 e) Hiçbiri 6. Kenar uzunluğu 1 birim olan karenin köşelerinden eş ikizkenar dik üçgenler kesilerek bir düzgün sekizgen elde ediliyor. Düzgün sekizgenin alanı kaç birim karedir? a) 2 3 b) 2 2 3 c) 2 1 d) 4 2 5 e) Hiçbiri 7. Bir tane 1, bir tane 2 ve istenildiği kadar 0 rakamı kullanılarak yazılabilecek 1010 dan küçük sayıların kaç tanesi bir tam sayının karesine eşittir? a) 0 b) 1 c) 1000 d) 3000 e) Hiçbiri 8. x 2 8 x 2 y 16 ve y 2 4 y 2 x 10 denklemlerinin sağlayan x, y reel sayıları için x y kaç farklı değer alabilir? 9. a ve b birbirinden farklı asal sayılar olsun. aaa ve bbb üç basamaklı sayılar olmak üzere (aaa bbb)2 çarpımının asal olmayan tüm bölenlerinin toplamı 48 ise, a·b kaçtır? a) 6 b)10 c) 15 d) 35 e) 55 8 a 7 eşitsizliğini sağlayan her bir a 15 a b 13 değerleri için en fazla iki tane b değeri bulunabiliyor. Buna göre a nın alabileceği en büyük değerin rakamları toplamı nedir? 10. a ve b birer pozitif tam sayı olmak üzere, ÇÖZÜMLER 1. Genel olarak A ile B arasındaki dikdörtgenin n dilime ayrılması durumunda gidilebilecek farklı yolların sayısının 2n dir. Problemde n 13 dilim olduğundan 213 8192 farklı yol vardır. Bunu ispat edelim. Üst yoldaki iki nokta arasında kalan doğru parçalarını a1 , a2 , … , a13 ile, alt yoldaki iki nokta arasında kalan doğru parçalarını b1 , b2 , … , b13 ile gösterelim. A dan B ye gitmek için a1 , b1 , a2 , b2 , … , a13 , b13 kümelerinin her birinden birer eleman seçmeliyiz. Bu ise 213 8192 yolla yapılabilir. a1 a2 a13 A B b1 b2 b13 2. Alan( ABCF ) ve Alan( BCDG) , beşgenin alanının yarısına eşit olduğundan aşağıdaki şekS le göre S1 S3 S2 S3 olup x 1 1 dir. S2 A S1 B E H S3 C G S2 F D 3. Verilen ifadeyi z x3 2 x 2 y 2 xy 2 y 3 ( x3 y 3 ) (2 x 2 y 2 xy 2 ) ( x y)( x 2 xy y 2 ) 2 xy( x y) şeklinde düzenlersek z ( x y )( x 2 3xy y 2 ) olur. x, y, z asal sayılar olduğundan z x 2 3xy y 2 1 x y olmalıdır. Aralarındaki fark 1 olan asal sayılar yalnızca 3 ve 2 dir. Dolayısıyla x 3, y 2 elde edilir. Bu değerler kullanılarak z nin tek değeri z 31 olarak bulunur. 4. CAB ve EFD eş üçgenler olduğundan AC EF , AB FD , BC DE dir. Bu eşitlik- lerden x y z 3 , z 6 2 y z , x 8z y 2 olup denklemler çözülürse x 2 , y 4 , z 1 dir. x3 y 3 z 3 (2)3 43 13 57 bulunur. 5. (k 1) (k 2) (k 3) ... (k 19) n 2 olsun. 19k 190 n2 olup 19(k 10) n2 yazılır. Son eşitlikte sol tarafın tam kare olması için k 10 19 m2 şeklinde olmalıdır. m 1 için k 9 , n 19 en küçük değeri bulunur. 19 dan sonraki en küçük değeri bulalım. m 2 için k 66 , n 38 bulunur. Bu k sayılarının toplamı 9 66 75 dir. 6. Eş ikizkenar üçgenlerin dik kenar uzunlukları x olsun. Düzgün sekizgenin alanı 1 2x2 olur. Ayrıca düzgün sekizgenin bir kenarı, kesilen dik üçgenin hipotenüsüne eşit olduğundan 2 2 bulunur. O halde düzgün sekizgenin alanı: 1 2 x 2 x olur. Bu eşitlikten x 2 2 2 2 1 2 x 2 1 2( ) 2 2 2 birim kare bulunur. 2 7. Oluşturacağımız sayıların rakamları toplamı daima 3 tür. Bu sayı bir tam sayının karesine eşit ise bu tam kare sayı 9 ile bölüne bilmelidir. Fakat bu mümkün olmadığından istenen şartları sağlayan sayı yoktur. 8. Denklemleri taraf tarafa toplayıp düzenlersek 2 2 x 2 10 x 25 y 2 2 y 1 0 x 5 y 1 0 x 5, y 1 olup x y tek değer alır. 9. Bir sayının asal olmayan tüm bölenlerin toplamı 48 ise asal bölenlerinin toplamı 48 dir. (aaa bbb)2 = a2 b2 32 372 olduğundan a + b = 8 dir. O halde a b 3 5 15 . 8 a 7 13 a b 15 6 b 7 6 b 7 6a 7a 1 1 1 b 15 a b 13 7 a 8 7 a 8 7 a 8 7 8 7 a 6a 6a 7 a eşitsizliğini elde ederiz. , aralığında en az iki tam sayı olması için 3 olma8 7 7 8 a lıdır. 3 a ≤ 168 elde ederiz. a = 168 için 144 b 147 olur. Yani b nin en az iki çö56 zümü vardır. 168 in rakamları toplamı 15 tir. 10.