NEWTON’UN HAREKET YASALARI
ZORU SEVENLERE
1. Sistemin ivmesi;
3mg = 6ma
g
a=
2
M nin hareket denklemi;
3mg − 2T = 3ma
•
•
→
F
↓
F
g
2
m1g
•
•
•
g
3mg − 2T = 3m
•
•
•
F
m1
F
N
m2
3mg
4
K nin hareket denklemi;
T − Fs = ma
T=
m2 g
N
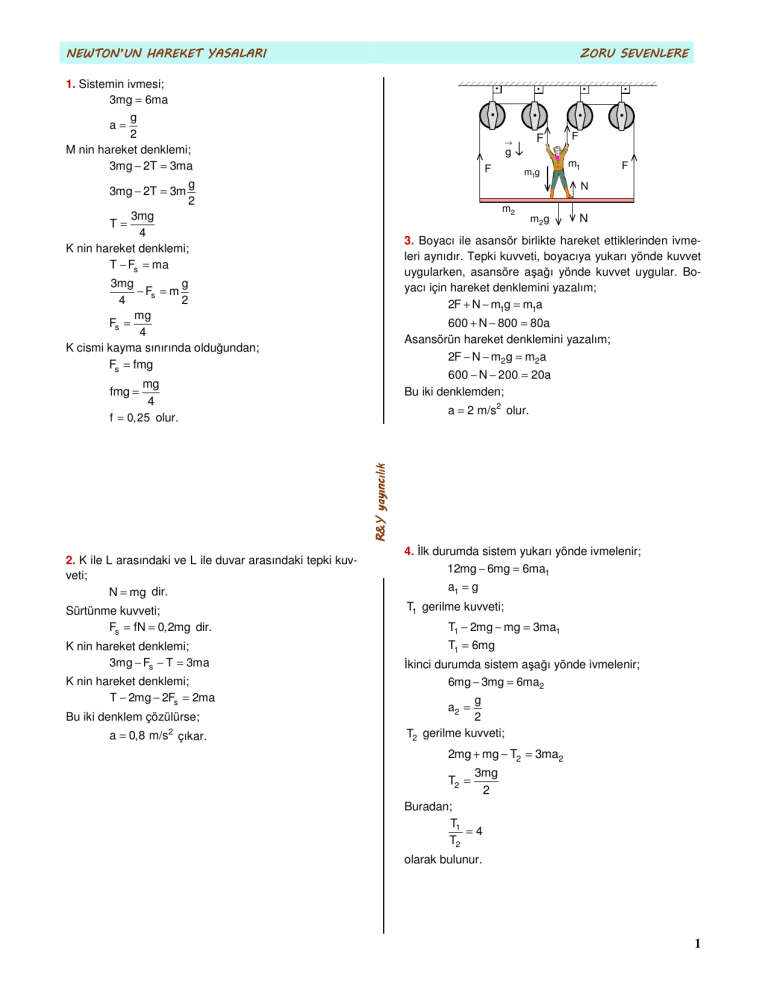
3. Boyacı ile asansör birlikte hareket ettiklerinden ivmeleri aynıdır. Tepki kuvveti, boyacıya yukarı yönde kuvvet
uygularken, asansöre aşağı yönde kuvvet uygular. Boyacı için hareket denklemini yazalım;
2F + N − m1g = m1a
3mg
g
− Fs = m
4
2
mg
Fs =
4
K cismi kayma sınırında olduğundan;
Fs = fmg
600 + N − 800 = 80a
Asansörün hareket denklemini yazalım;
2F − N − m2 g = m2a
600 − N − 200 = 20a
Bu iki denklemden;
mg
4
f = 0,25 olur.
fmg =
R&Y yayıncılık
a = 2 m/s2 olur.
2. K ile L arasındaki ve L ile duvar arasındaki tepki kuvveti;
N = mg dir.
Sürtünme kuvveti;
Fs = fN = 0,2mg dir.
K nin hareket denklemi;
3mg − Fs − T = 3ma
K nin hareket denklemi;
T − 2mg − 2Fs = 2ma
Bu iki denklem çözülürse;
a = 0,8 m/s2 çıkar.
4. İlk durumda sistem yukarı yönde ivmelenir;
12mg − 6mg = 6ma1
a1 = g
T1 gerilme kuvveti;
T1 − 2mg − mg = 3ma1
T1 = 6mg
İkinci durumda sistem aşağı yönde ivmelenir;
6mg − 3mg = 6ma2
g
2
T2 gerilme kuvveti;
a2 =
2mg + mg − T2 = 3ma2
T2 =
3mg
2
Buradan;
T1
=4
T2
olarak bulunur.
1
NEWTON’UN HAREKET YASALARI
ZORU SEVENLERE
5. İlk durumda sistemin ivmesi;
7. İlk durumda sistemin ivmesi;
F
F1 = 6ma1 ⇒ a1 = 1
6m
M nin hareket denklemi;
F
T = 3ma1 ⇒ T = 1
2
F1 = 2T
3mg − 2mg g
=
3m + 2m
5
İlk durumdaki gerilme kuvveti;
T1 − 2mg = 2ma1
a1 =
12mg
5
Dinamometrenin gösterdiği değer;
24mg
F1 = 2T1 =
olur.
5
İkinci durumda sistemin ivmesi;
4mg − 2mg g
a2 =
=
4m + 2m
3
İkinci durumdaki dinamometrenin gösterdiği değer;
3mg − F2 = 3ma2
T1 =
İkinci durumda sistemin ivmesi;
F
F2 = 6ma2 ⇒ a2 = 2
6m
K nin hareket denklemi;
F
2T = ma2 ⇒ a1 = m 2
6m
F2 = 12T
Üçüncü durumda sistemin ivmesi;
5T
12T − 2T = 4ma3 ⇒ a3 =
2
M nin yeni hareket denklemi;
12T − T' = 3ma3
F2 = 2mg
Buradan;
F1 12
=
F2
5
9T
2
olarak bulunur.
olarak bulunur.
R&Y yayıncılık
T' =
8. Birinci durumdaki minimum kuvvet;
F1 = Fs1
F1 = 3fmg olur.
6. Cisimlerin birlikte gitmesi ve L nin ivmesinin maksimum olması isteniyor. Bu durumda K ile L arasındaki
statik sürtünme kuvveti maksimum olmalıdır. L nin hareket denklemini yazalım;
Fs3 − Fs2 = mK a ⇒ 0,5.2mg − 0,2.3mg = ma
a = 0,4g
Bu ivme aynı zamanda sisteminde ivmesidir.
F − Fs1 − Fs2 = 6ma
F − 0,2.3mg − 0,4.3mg = 6m.0,4g
F = 4,2mg
olarak bulunur.
2
İkinci durumdaki minimum kuvvet;
2F2 = Fs2
2F2 = 4fmg
F2 = 2fmg
Buradan;
F2 2
= olur.
F1 3
NEWTON’UN HAREKET YASALARI
ZORU SEVENLERE
11. İlk durumda sistemin ivmesi;
4mg − 3mg = 3ma1
9. K cisminin hareket denklemi;
F1 − T − 2mg = 2ma
g
3
T gerilme kuvveti;
F1 − 3mg − 2mg = 2mg
a1 =
F1 = 7mg
L cisminin hareket denklemi;
T − F2 − mg = ma
T − 2mg = 2ma
3mg − F2 − mg = mg
8mg
3
İkinci durumda sistemin ivmesi;
T=
F2 = mg
İp koptuktan sonra K nin ivmesi;
F1 − mg = ma1
a1 =
g
3
İpteki gerilme kuvveti;
4mg + mg − T ' = ma2
5g
2
8mg
3
T' = T
olarak bulunur.
T' =
L nin ivmesi;
F2 + mg = ma2
a2 = 2g
Buradan;
a1 5
olarak bulunur.
=
a2 4
F
K
3m
→
12. İlk durumda;
F'
↓
K
T=6mg
a
a'
L
2m
M
L
m
Şekil 1
Şekil 2
10. L ile M nin hareket denklemini yazalım;
T − 3mg = 3ma
6mg − 3mg = 3ma
a=g
R&Y yayıncılık
↓
g
g
→
2F − f ( mg + F ) = 5ma
(1)
İkinci durumda;
2F − f ( mg − F ) = 7ma
( 2)
Üçüncü durumda;
F − fmg = 2ma
(3)
olur. Bu üç denklem çözülürse;
F = 4ma
fmg = 2ma çıkar.
Dördüncü durumda cismin ivmesi;
3F − fmg = ma 4
12ma − 2ma = ma 4
a 4 = 10a
olarak bulunur.
K nin hareket denklemini yazalım;
F − 6mg = 6ma ⇒ F = 12mg
Yeni kuvvet
F
=3mg
4
Yeni sistemin ivmesi;
F’=
2g
5
Dinamometrenin gösterdiği yeni değer için L nin hareket
denklemini yazalım;
6mg
2mg − T' = 2ma' ⇒ a' =
olur.
5
5mg − 3mg = 5ma' ⇒ a' =
3
NEWTON’UN HAREKET YASALARI
ZORU SEVENLERE
15. İlk durumda K ile L nin ivmeleri;
F = mK aK1
13. İlk durumdaki sistemin ivmesi;
F − ( mK + mL + mM ) g = ( mK + mL + mM ) a1
a1 =
12 = 6aK1 ⇒ aK1 = 2 m/s2
F
−g
(mK + mL + mM )
F = mL aL1
12 = 3aL1 ⇒ aL1 = 4 m/s2
D2 dinamometrenin gösterdiği değeri kullanalım;
T − mL g = mL a1 ⇒ T =
F=
Cisimlerin kazandıkları hızlar;
v K1 = aK1t = 2.5 = 10 m/s
mLF
( mK + mL + mM )
vL1 = aL1t = 4.5 = 20 m/s
(mK + mL + mM ) T
Aldıkları yollar;
mL
0 + vK1
10.5
= 25 m
xK1 =
t =
2
2
İkinci durumdaki sistemin yeni ivmesi;
F
( mK + mL + mM ) g − = (mK + mL + mM ) a2
2
T
a2 = g −
(1)
2mL
0 + vL1
20.5
xL1 =
= 50 m
t =
2
2
İkinci durumda cisimlerin ivmeleri;
D1 dinamometrenin gösterdiği değeri kullanalım;
24 = 6aK2 ⇒ aK2 = 4 m/s2
(mK + mL ) g − 4T = (mK + mL ) a2
4T
m
( K + mL )
Cisimlerin kazandıkları hızlar;
v K 2 = v K1 + aK 2 t = 10 + 4.5 = 30 m/s
( 2)
(1) ve (2) nolu denklemler kullanılırsa;
mK
=7
mL
olarak bulunur.
vL2 = vL1 + aL2 t = 20 + 2.5 = 30 m/s
Cisimlerin aldıkları yollar;
R&Y yayıncılık
a2 = g −
6 = 3aL2 ⇒ aL2 = 2 m/s2
xK2 =
xL2 =
( vK1 + vK2 ) t (10 + 30 ).5
2
=
2
( vL1 + vL2 ) t = ( 20 + 30 ).5 = 125 m
2
iki cisim arasındaki uzaklık
2
∆x = ( xL1 + xL2 ) − ( xK1 + xK2 )
14. Her iki cisim aynı ipe bağlı olduğundan, cisimlerin
aldığı yollar, kazandıkları hızlar ve ivmeler aynı olur. Yatayda, F kuvvetinin dışındaki kuvvetler iç kuvvettir. Bu
yüzden bu kuvvetler cisimleri ivmelendirmez.
F = ( m1 + m2 ) a ⇒ 30 = 6a; a = 5 m/s2
Cisimlerin 2 s sonraki hızı ve aldığı yol;
v1 = at = 5.2 = 10 m/s
x=
( v 0 + v1 ) t = ( 0 + 10 ) .2 = 10 m
olarak bulunur.
4
2
2
= 100 m
∆x = 175 − 125 = 50 m
olarak bulunur.
NEWTON’UN HAREKET YASALARI
ZORU SEVENLERE
16. L cismi ile ip arasındaki sürtünme kuvveti, L cismi
için yukarı yönlü iken, ip için aşağı yönlüdür. Buna göre,
K ve L cisimlerin ivmeleri;
mL g − Fs = mL aL
18. K nin hareket denklemini yazalım;
T − F1 + mg = ma
3mg − F1 + mg = 2mg
F1 = 4mg
20 − 10 = 2aL ⇒ aL = 5 m/s2
L nin hareket denklemini yazalım;
F2 − T + mg = ma
mK g − Fs = mK aK
30 − 10 = 3aK ⇒ aK =
F2 − 3mg + mg = 2mg
20
m/s2
3
F2 = 4mg olur.
K ile L nin kazandıkları hızlar;
vK = aK t = 5t
20t ;
vL = aL t =
3
Cisimlerin aldıkları yollar;
0 + vK
xK =
2
xL =
İp koptuktan sonra cisimlerin ivmesi;
F1 − mg = maK
2mg − mg = maK
aK = g
F2 + mg = maL
5t 2
t =
2
2mg + mg = maL
aL = 5g
( 0 + vL ) t = 10t 2
K nin hızı sıfır olması için geçen süre;
v
0 = v − aK t ⇒ t =
g
2
3
K nin L yi yakalama süresi;
h = xL − xK
2
2
Bu anda L nin hızı;
2
10t
5t
5t
−
=
3
2
6
t = 6 s olur.
v 2 = v + aL t = v + 5g
17. F ( t ) kuvveti, K ile L ye etki eden sürtünme kuvveti-
ne eşit olduğunda cisimler harekete geçer. Bunun için
gereken süre;
3mg
FsK + FsL = 0,5.3mg =
2
3mg
kt1 =
2
3mg
t1 =
olur.
2k
K ile L arasındaki ip gerilme kuvveti 4mg olduğundaki K
nin hareket denklemini yazalım;
T − FsK = mK
R&Y yayıncılık
30 =
v
g
v 2 = 6v olur.
4mg − 0,5.2mg = 2ma
3g
a=
2
Bu durum için sistemin hareket denklemini yazalım;
kt 2 − FsK − FsL = ( mK + mL ) a
3mg
3g
= 3m.
2
2
6mg
t2 =
k
Buradan
t1 1
= olur.
t2 4
kt 2 −
5
NEWTON’UN HAREKET YASALARI
ZORU SEVENLERE
20. İlk durumda cisimlerin ivmesi;
F − Fs − mg = 2ma1
19. İlk durumda cisimlerin ivmeleri;
6mg − 4mg = 10ma1 ⇒ a1 =
g
5
3mg − 0,5mg − mg = 2ma1
Cisimlerin t sürede kazandığı hız;
3g
4
Cisimlerin t süre sonra kazandığı hız;
3gt
v = a1t =
4
F kuvveti kaldırılıp cisimler durana kadar olan ivme;
Fs + mg = 2ma2
a1 =
gt
v1 = a1t =
5
Cisimlerin t sürede aldığı yol;
K cismi L ile karşılaşıncaya kadar
h1
kadar yol alır.
2
h1 0 + v1
gt 2
=
t
=
2 2
10
0,5.mg + mg = 2ma2
3g
4
Cisimler durana kadar geçen süre;
0 = v − a2 t 2
4v
t2 =
=t
3g
2
gt
5
M ile N arasındaki ip koptuktan sonra sistemin ivmesi;
6mg − 2mg = 8ma2
a2 =
h1 =
g
2
Sistemin ip koptuktan t süre sonra kazandığı hız;
gt gt 7gt
v2 = v1 + a2 t = + =
5 2 10
h
K ile M cismi karşılaşıncaya kadar 2 yol alır.
2
gt 7gt
5 + 10
h2 ( v1 + v 2 )
t
=
t=
2
2
2
a2 =
h2h1
6
mg − 0,5.mg = 2ma3
g
4
Cisimlerin v hızına ulaşıncaya kadar geçen süre;
v = a3 t3
a3 =
R&Y yayıncılık
9 gt 2
h2 =
2 5
Buradan;
9
olur.
=
2
Cisimler ters yönde hızlanırken ivme;
mg − Fs = 2ma3
t3 =
4v
= 4t
g
Toplam süre;
T = 6t olur.
NEWTON’UN HAREKET YASALARI
ZORU SEVENLERE
21. İlk durumda cisimlerin ivmeleri;
3mg − 2mg = 5ma1 ⇒ a1 =
22. Tahta ile zemin arsındaki sürtünme kuvveti;
Fs1 = f (mc + mt ) g = 0,2.80
g
5
Fs1 = 16 N
Cisimlerin t sürede kazandığı hız;
Cisim ile tahta arasındaki sürtünme kuvveti;
Fs2 = fmc g = 0,2.10
gt
5
Cisimlerin t sürede aldığı yol;
v1 = a1t =
Fs2 = 2 N
Tahtanın hareket denklemi;
F − Fs1 − Fs2 − T = mt a
0 + v1
gt 2
h1 =
t =
10
2
L cismi makaranın diğer tarafına geçtiğinde ivme;
4mg − mg = 5ma2
24 − 16 − 2 − T = 7a
Cismin hareket denklemi;
T − Fs2 = mc a
3g
5
t sürede kazandıkları hız;
gt 3g
4gt
v 2 = v1 + a 2 t =
+
t=
5
5
5
Cisimlerin t sürede aldığı yol;
gt 4gt
+
t
v1 + v 2 ) t 5
(
5
h2 =
=
2
2
a2 =
h2 =
T − 2 = 1.a
( 2)
(1) ve (2) numaralı denklemler çözülürse;
a = 0,5 m/s2 çıkar.
Cisimlerin kazandıkları hızlar;
v = at = 0,5t
Cisimlerin aldıkları yollar;
t2
0+v
x=
t=
4
2
ℓ = 2x
gt 2
2
ℓ = 2.
h2h1
t2
4
t2
⇒t=2s
2
olarak bulunur.
= 5 olur.
2=
R&Y yayıncılık
Buradan;
(1)
7
NEWTON’UN HAREKET YASALARI
ZORU SEVENLERE
23. İlk durumda cisimler dengededir;
F = 4mg
24. F kuvveti uygulanırken sistemin ivmesi;
F − Fs − mg = 2ma1
M ile N arasındaki ip koptuktan sonra;
g
F − 3mg = 3ma1 ⇒ a1 =
3
gt
v1 = a1t =
3
0 + v1
gt 2
h=
t =
6
2
2mg − 0,5.mg − mg = 2ma1
g
4
t sürede kazandıkları hız;
gt 10.12
v1 = a1t =
=
4
4
= 30 m/s
a1 =
L ile M arasındaki ip koptuktan sonra;
F − 2mg = 2ma2 ⇒ a2 = g
Cisimlerin aldığı yol;
0 + v1
30.12
x1 =
= 180 m
t =
2
2
F kuvveti kaldırıldıktan sonra cisimler durana kadar olan
ivme;
Fs + mg = 2ma2 ⇒ 0,5.mg + mg = 2ma2
gt
v 2 = v1 + a2 t =
+ gt
3
4gt
v2 =
3
gt 2
v + v2
h2 = 1
t = 5.
6
2
3.10 15
=
m/s2
4
2
Cisimlerin durma süresi;
a2 =
h2 = 5h
K ile L arasındaki ip koptuktan sonra;
F − mg = ma3 ⇒ a3 = 3g
4gt
+ 3gt
3
13gt
3
v2 + v3
gt 2
h3 =
t = 17.
2
6
h3 = 17h
v3 =
3t sürede aldığı toplam yol;
H = 23h
olarak bulunur.
R&Y yayıncılık
v 3 = v 2 + a3 t =
0 = v1 − a2 t 2 ⇒ 0 = 30 −
15
t
2
t=4s
Cisimlerin duruncaya kadar aldığı yol;
30.4
v +0
x2 = 1
t =
2
2
= 60 m
Cisimler geri döndükten sonra hızlanırken ivmeleri;
mg − Fs = 2ma3 ⇒ mg − 0,5.mg = 2ma3
g
4
Hızın aynı büyüklükte olana kadar geçen süre;
10t 3
v = a3 t3 ⇒ 30 =
4
t3 = 12 s
a3 =
Bu sürede alınan yol;
vt
30.12
x3 = 3 =
= 180 m
2
2
K nin ilk konumundan olan uzaklık;
∆x = x1 + x 2 − x3 = 60 m
olarak bulunur.
8