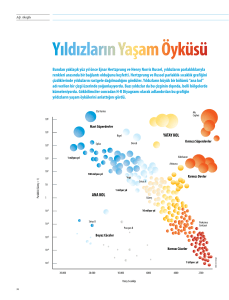
Yıldızların uzaklıkları ve parlaklıkları
Güneş’in İç Yapısı
Güneş
enerjisinin üretildiği bölge,
tepkimelerini yer aldığı özek bölgesidir.
çekirdek
Bu enerji dış katmanlara taşınmakta oradan da uzaya
yayılmaktadır.
Gök bilimciler, Güneşte esas olarak ışınımla ve
konveksiyonla (kütle hareketleriyle) taşındığını
savunurlar. Özek bölgesini çevreleyen ve enerjinin
ışınım yoluyla taşındığı bölgeye, ışımasal bölge denir.
Özekte üretilen bir foton Güneş’in yüzeyine bir doğru
boyunca ulaşamaz, fakat yıldız maddesi ile çarpışır,
saçılır, soğurulur ve yeniden salınır.
Hesaplar gösteriyor ki, tek bir fotonun yüzeye ulaşması
bir milyon yıl almaktadır.
Yani, bizim şimdi gözlediğimiz güneş ışığı, özekte
bundan bir milyon yıl önce üretilmişti.
Bu nedenle biz Güneş’in özeğini değil fotonların en
son salındığı dış katmaları görüyoruz.
Işımasal bölgeyi çevreleyen bir sonraki katman
konvektif zardır.
Burada enerji, katmanlardaki maddenin hareketi ile
taşınır. Sıcak gazlar yükselip taşıdığı enerjiyi ışık
küreye bırakır, soğur ve geri dönüp yeniden ısınır.
Güneşin Manyetik Etkileri
Galileo, 1610 yılında yaptığı gözlemler sonucu Güneş
yüzeyinin kusursuz
olduğunu keşfetti.
değil,
siyah
lekelerle kaplı
Bunların bir kısmı beyaz ışık fotoğrafında görülebilir.
Beyaz alanlarla da çevrili olan bu güneş lekeleri
çoğunlukla ikişerli olarak ortaya çıkar ve gruplar
halinde kümeleşir.
Bu lekeler aslında siyah olmaktan uzaktır.
Fakat 4500 K sıcaklığında olduğundan 5800 K den
daha yüksek sıcaklıktaki çevresine göre daha koyu
gözükürler.
Güneş lekeleri Güneşle birlikte döndüklerinden,
Güneş’in döndüğünü çok iyi gösterirler.
Ekvator bölgesi 25 günde bir döner, bu yavaşlayarak
kutuplarda yaklaşık 34 günü bulur.
Böylece Güneş, enleme göre diferansiyel dönme
gösterir.
Güneş lekelerinin manyetik alanlarla ilgili olduğu
anlaşılmıştır.
Çeşitli tekniklerle yapılan gözlemler, Güneşte güçlü
manyetik alanların var olduğunu göstermiştir.
Leke yakınlarında şiddetleri, Yer’in manyetik alanının
3000 katına ulaşabilmektedir.
Alan çizgileri bir leke çiftinin birinden çıkıp ilmek
oluşturarak diğerine girerler.
Büyük olasılıkla lekeleri güçlü manyetik alanlar üretir.
Bu bağlamda güneş lekeleri manyetik ilmeklerin ışık
küredeki kesitleridir.
Büyük manyetik ilmekler ışık küreden 400000 km
yükseklere kadar uzanırlar.
Güneş Rüzgarı
Güneş’in ışık, radyo ve x-ışınları gibi her yöne
elektromanyetik dalgalar gönderdiğini biliyoruz.
Olay yalnız bu değildir.
Güneş’ten her yöne sürekli parçacıklar aksısı vardır.
Bunlar çoğunlukla elektronlar ve protonlardır.
Güneşin taç katmanından bu şekilde uzaya sürekli
madde kaybı vardır.
Buna güneş rüzgarı denir.
Uydularla yapılan gözlemler göstermiştir ki Yer
yakınlarında 1 cm3 den ortalama 10 kadar proton ve
elektron geçer; ortalama hızları 400 km/s kadardır.
Bir bakıma biz Güneş taç katmanının dış uzantıları
içindeyiz.
Bu rüzgarın hızı değişkendir ve Güneş’in manyetik
çevrimine bağlıdır.
Güneş rüzgarı ayrıca Yer’in manyetik
alanına da rüzgar yönünde şok dalgası
biçiminde sıkıştırır.
Deniz hız motorunun önündeki suda
oluşturduğu ve iki yandan arkaya
uzanan dalga gibi.
Bu
dalga sınırları içinde yüklü
parçacıklar olarak, Van Allen kuşakları
denen iki bölgede hapsedilirler.
Güneş rüzgarının basıncı sonucu
Yer’in arka tarafında 100 Yer
yarıçapını
aşan
uzunluklarda
manyetik kuyruk oluşur.
Güneş sisteminde manyetik alanı
olan bütün gezegenler
rüzgarından etkilenir.
Güneş
Güneş’in manyetik etkinliğinin ve Güneş rüzgarının
Yer üzerinde başka önemli etkileri de vardır.
Taç katmanında büyük bir parlama olduğu zaman,
özellikle Güneş leke maksimumu sırasında, artan
güneş rüzgarı şiddeti yaklaşık iki gün sonra Yer’e ulaşır.
Yer’in manyetik alanlarını sıkıştırır ve kutup akım
halkalarına büyük miktarda enerji bırakır.
Bu güçlü elektrik akımı üst atmosferdeki havayı
iyonlaştırır.
Elektronlarla havanın aynı atom ve moleküllerinin yeniden
birleşmesi “kutup ışığı” (güneyde ve kuzeyde) denen ışık
gösterisi biçiminde göğü aydınlatır.
Böyle “manyetik fırtınaların” radyo haberleşmelerini etkilediği,
zaman zaman elektrik hatlarında arızalara neden oldukları
bilinmektedir.
Yıldızların uzaklıkları
Yıldızların bize uzaklıkları çok farklıdır. Onların
büyüklük, ışınım gücü gibi gerçek özelliklerini
bulabilmek için önce uzaklıklarını bilmeliyiz.
Şimdi en azından yakın yıldızların uzaklıklarının nasıl
bulunduğunu görelim:
İşaret parmağınızı gözlerinizden 30 cm kadar uzakta
tutunuz ve parmağınızın ucuna önce bir gözünüzle
sonra diğer gözünüzle bakınız.
Çok uzaktaki cisimlere göre parmağınızın ucunun belli
bir açı kadar yer değiştirdiğini görürsünüz.
Parmağınızı uzaklaştırdıkça yer değiştirme açısı da
küçülür.
Şimdi aynı işi çok uzaktaki bir cisimle yapınız; yer
değişme olmadığını göreceksiniz. Yer değiştirme açısı,
cismin gözünüzden uzaklığının bir ölçüsüdür.
Bu
ilke genişletilerek,
yıldızların
uzaklığının
bulunmasında kullanılır.
Yer’in Güneş çevresindeki
yörüngesini ve bu yörünge
düzlemi içinde bir Y
yıldızı ele alalım
Yer A konumunda iken Y yıldızı
AY’ doğrultusunda görülür.
Altı ay sonra Yer B konumuna
geldiği zaman aynı Y yıldızı bu
kez BY’’ doğrultusunda görülür.
Bir
yıl sonra Y yine
doğrultusunda olacaktır.
Y’
p
açısına Y yıldızının
Güneş merkezli ıraklık
açısı (paralaks) denir.
Yani ıraklık açısı Yer-Güneş
uzaklığını yıldızdan gören
açıdır.
AYG üçgeninde p açısı ve
AG uzunluğu bilindiğine
göre
geometrik
yöntemlerle;
Bir dairede iki ayrı yay parçalarının uzunluklarının
oranı, bu yayları gören merkez açılarının oranına
eşittir.
Dairenin çevresi 2πr ve bu çevreyi gören merkez açı
360o olduğuna göre (BG/2πr)=(po/360o) yazılabilir.
p küçük olduğu için açı saniyesi cinsinden ifade etmek
adet olmuştur.
O zaman 360o yi de açı saniyesi cinsinden yazmalıyız:
𝐴𝐺
2πr
𝑟=
=
𝑝′′
360×60×60
206265 ×𝐴𝐺
𝑝′′
AG= 1 GB (gök birimi) olduğuna göre, GB cinsinden;
𝑟=
206265
𝑝′′
GB
Astronomide 206265 GB uzunluğuna 1 parsek denir ve
kısaca pc yazılır.
O zaman pc cinsinden r, basitçe r=1/p parsek olur. O
halde parsek, Yer-Güneş uzaklığını 1 açı saniyesi
altında gören yıldızın uzaklığıdır, o da 206265 GB’ne
eşittir.
Kullanılan bir başka uzaklık birimi ışık yılıdır, bu ışığın
bir yılda aldığı yoldur.
1 parsek = 3.26 ışık yılı olduğunu kolayca
gösterebilirsiniz.
Bize en yakın yıldızın (Proxima Centauri) ıraklık açısı
p=0.75’’ dir.
Bu uzaklık için r = 1/0.75 =1.33 parsek = 4.3 ışık yılı
verir.
Iraklık açılarının ölçülmesi çok zordur ve yıllar süren
gözlemler gerektirir.
Böyle
küçük
karışmaktadır.
açıların
ölçülmesine
ölçü
hataları
Ölçülebilen en küçük açı 0.01’’ kadardır, bu 100 pc
demektir.
Bu yüzden 100 pc den daha ötedeki uzaklıklar için bu
yöntem yararsızdır.
Örnek: Bir X yıldızının paralaksı 0,012 açı saniyesidir.
Bir Y yıldızının Yer’e olan uzaklığı ise 83,4 pc dir.
a) Hangi yıldız bize daha yakındır?
b) İki yıldız arası uzaklık farkı kaç km’dir?
Çözüm:
a) r = 1/p’’ = 1 / 0,012 = 83,33 pc
b) 1 pc = 206265 GB, 1 GB= 149,6 106 km
0,07 pc = 0,07 × 149,6 106 km × 206265
= 2,16 1012 km
Yıldızların parlaklıkları
Yıldızları incelemede bilinmesi gerekenlerin başında
onların parlaklıkları gelir.
M.Ö. ikinci yüzyılda Hipparchus çıplak gözle
görebildiği yıldızların parlaklıklarını kadir aralıkları
denen beş aralığa böldü.
En parlak yıldızı 1. kadir, en sönük yıldızı 6. kadir
olarak sınıfladı.
Yıldızların gökteki konumlarını ve parlaklıklarını
içeren ilk kataloğu hazırladı.
Örneğin Büyük ayı’nın yıldızlarının çoğu ve kutup
yıldızı 2. kadirden, Küçük
sapındakiler 4. kadirdendir.
ayı’nın
tavasının
“Kadir” birimi rakamın üzerine yazılan m harfi ile
gösterilir. Ör: 2m ikinci kadir, 3m,6 üç onda altıncı kadir
demektir
Bugün teleskoplar sayesinde 6m den daha sönük
milyarlarca yıldız olduğunu biliyoruz.
Bunların
parlaklıkları, Hipparchus ölçeğini de
koruyarak fakat kişinin göz yeteneğine bağlı olmayan,
iyi tanımlanmış çağdaş aletlerle ölçülen sayısal kadir
sınıfına dayandırılmıştır.
Gök cismi
Parlaklık
Güneş
-26m.5
Dolunay
-12m.5
Venüs (en parlak)
-4m.4
Sirius
-1m.4
Rigel
0m.0
Aldebaran
+1m.0
Kutup yıldızı
+2m.0
Çıplak gözle görme sınırı
+6m.0
Yıldız parlaklıklarını ölçmek için temelde iki çeşit
yöntem vardır.
Birincisi 19. Yüzyıl sonlarında başlayan ve bugün çok
daha duyarlı hale getirilen fotoğraf çekme yöntemidir.
Bir yıldızın görünen parlaklığı, fotoğraf filmi üzerinde
oluşturduğu görüntünün büyüklüğünden bulunabilir.
Parlak bir yıldızın film üzerindeki görüntüsü sönük
yıldızın görüntüsünden daha büyük olur.
Bunlar “fotoğrafik ışıkölçer” diye bilinen aletlerle
ölçülürler.
Daha duyarlı ikinci yöntem “fotoelektrik ışık ölçümü”
yöntemidir. Işık fotonları ışığa duyarlı bir yüzeye
düştükleri zaman, yüzeyden elektron koparırlar.
Ne kadar çok foton düşerse o kadar çok elektron
koparılır.
Bu elektronlar elektrik akımı oluşturur. Bu akımın
şiddeti ışığa duyarlı yüzeye düşen ışığın şiddetinin bir
ölçüsüdür.
19. yüzyıl gök bilimcileri, birinci kadirden yıldızların
altıncı kadirden yıldızlara göre 100 kat daha parlak
olduğunu buldular.
Kadir farkı 5 iken parlaklık oranının 100 olması demek,
kadir farkı 1 iken parlaklık oranının 2.512 olması
demektir. Çünkü;
x5 = 100 x= 2.512
Bir yıldız diğerinden iki kadir daha parlak demek;
(2.5)(2.5)=6.3 kere daha parlak demektir.
Salt parlaklıklar
Bir ışık kaynağının görünen parlaklığı, uzaklığın karesi
ile orantılı olarak değişir.
Uzaklığı iki katına çıkarsa bize ulaşan ışık miktarı dört
kat azalır.
Çünkü bir nokta kaynaktan çıkıp bir koni içinde
yayılan ışık, koninin eksenine dik kesitinin alanı
gittikçe büyüdüğünden, gittikçe daha büyük alana
yayılır.
İki alanın oranı, bu alanların koninin köşesine olan
uzaklıklarının kareleri oranına eşittir.
O
halde
yıldızların
karşılaştırabilmek için
indirgemeliyiz.
gerçek
hepsini
parlaklıklarını
aynı uzaklığa
Yıldızların hepsini 10 parsek ya da 32.6 ışık yılı uzaklığa
yerleştirdiğimizi
ve
ölçtüğümüzü düşünelim.
parlaklıklarını
yeniden
Bu şekilde bulunan kadir değerlerine salt (mutlak)
parlaklık denir.
Eğer bir yıldızın uzaklığı biliniyorsa salt parlaklık şu
formülden kolayca hesaplanır:
M = m + 5 – 5 log r
Burada; M salt parlaklık, m görünen parlaklık, r ise pc
biriminde uzaklıktır. Güneş’in salt parlaklığı:
M = -26.74 + 5 – 5 log (1/206265) = +4m.83