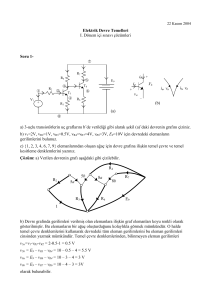
DENEY NO: 6
1.) ORTAK EMETÖRLÜ KUVVETLENDİRİCİLER
DENEY MALZEMELERİ:
BC237 npn transistör
87kΩ, 9.1kΩ, 3.3kΩ, 8.2kΩ, 100 Ω, 2x1kΩ, 10 kΩ’luk potansiyometre
2x10μF, 1nF, 470μF kondansatör
bağlantı telleri ya da krokodiller
NOT: Devre elemanlarının yanma olasılığına karşın önemli olanların yedeğinin
alınması tavsiye edilir.
GİRİŞ: Bir işaret kaynağı tarafından girişine uygulanan küçük genlikli işaretleri,
çıkış ucuna bağlı bulunan yüke, kuvvetlendirerek veren devreye yükselteç adı
verilir.
Yarıiletken devre elemanlarının istenen çalışma noktasında çalışması için
uçlarına belirli bir DA işareti uygulanmalıdır. Örneğin Silisyumdan yapılmış
1N4001 diyodunun iletime geçmesi için en az 0.6-0.7V’ luk bir gerilimin
uygulanması gerekir. Aynı şekilde yükselteçlerde kullanılan transistörlerin baz
uçları, dirençler kullanılarak öngerilimlenir. Devrede kullanılan transistörün
kutuplama akım ve geriliminin değeri devrenin kullanım alanına göre seçilir.
Kuvvetlendiricinin girişine küçük genlikli değişken işaret yani aa işaret
uygulanmadan önce DA besleme kullanarak transistörün istenilen çalışma
noktasında çalıştırılması amaçlanmaktadır. Girişte işaret yokken devrenin
çektiği akımlara boşta çalışma ya da sükunet(quiscent) akımı adı verilir. Yük
doğrusunu çizebilmek için transistörün kesim ve doyumda olduğu noktalar
saptandıktan sonra bu iki nokta Şekil 6.3’ de görülen grafik üzerinde bir doğru
meydana getirecek şekilde birleştirilir. Bu doğruya DA yük doğrusu denir.
Belirlenen değerlere göre transistörün çalışma noktaları bu doğru üzerinde
olur. Bir transistörün yükselteç olarak çalışması için emetör-baz ekleminin ileri,
kolektör-baz ekleminin ters yönde kutuplanması gereklidir.
+ Vcc
Rc
R1
C2
C1
RE1
Ry
Vg
R2
CE
RE2
Ri
Ro
Şekil 6.1. Ortak emetörlü yükselteç
1
Vo
Uygulamada kullanılan yükselteçlerin %90’ı ortak emetörlü yükselteçlerdir. Bu
tip çalışmada direnç değerleri VC gerilimi, VCC besleme geriliminin yarısı
olacak şekilde seçilir. Şekil 6.1’ de ortak emetörlü devre görülmektedir.
Devrede, çalışma noktası DA akım ve gerilim değerlerinin Ry yükünden ve
işaret kaynağından etkilenmemesi için C1 ve C2 kondansatörleri kullanılmıştır.
Bu kondansatörlere bağlama kondansatörleri denir. Emetör dirençleri R E1 ve
RE2 dirençlerinden oluşmaktadır. CE kondansatörü, devrede DA bileşenleri
yalıtmak amacıyla kullanılmaktadır. Bu kondansatör RE2 direncine paralel bağlı
olduğundan RE2 direncini aa işaretler açısından kısa devre etmektedir. CE
kondansatörüne atlatma kondansatörü denir.
Girişte işaret yokken besleme gerilimi verildiğinde devredeki kondansatörler
çalışma noktasına karşılık gelen doğru gerilimle dolar. Kondansatörün tanımı
gereği, uçları arasındaki gerilim sabit kaldığında akan akım sıfırdır. Buna göre
devrenin çalışma noktası büyüklükleri hesaplanırken bağlama ve atlatma
kondansatörleri açık devre alınmalıdır. R1 ve R2, baz bölücü kutuplama
devresidir. CE , doğru bileşenler açısından açık devre alındığında RE=RE1+RE2
direnci olduğu görülür.
Devrenin girişine aa işaret uygulandığında kondansatörlerin reaktansı 1 / C ,
çalışma frekansında devredeki direnç değerlerine göre çok küçük
olduğundan bu frekans aralığında C1, C2 ve CE kısa devre kabul edilir.
Besleme gerilimi sabit bir değer olduğundan aa işaretler için kısa devre
olduğu kabul edilir. Şekil 6.2’ de devrenin aa işaretler eşdeğer devresi
görülmektedir.
Vo
c
b
e
Vg
R1
R2
RE1
Rc
Ry
Şekil 6.2. aa işaretler eşdeğer devresi
Bu devrede görülen paralel dirençler yerine eşdeğerleri kullanıldığında
R y RC // R y
'
RC R y
RC R y
RB R1 // R2
R1 R2
R1 R2
olacaktır. aa işaretler açısından emetörde bulunan direnç Re=RE1’ dir.
Devrede R y kuvvetlendiricinin yükü, R 'y ise transistörün kolektörü ile devrenin
toprağı arasına gelen aa işaret eşdeğer direncidir. Transistörün kolektör
çevrimine giren aa işaretler açısından toplam direnç R AC R 'y R e ile
hesaplanır. Transistörün doğru akım yükü RDC, değişken işaret yükü RAC’ dir.
RDA, RC ve RE dirençleri toplamına eşittir.
2
Transistörün girişine aa işaret uygulanmadığında kolektör akımı I C ve kolektöremetör gerilimi VCE gerilimi çalışma noktası Q’ ya karşılık gelen değerdir. aa
işaret uygulanınca I C akımı, RC ve Ry arasında paylaşılır. Bu yüzden VCE gerilimi
RAC direncinin değişinden etkilenmektedir. Hem aa yük doğrusu hem de DA
yük doğrusu çalışma noktasından geçmektedir. DA yük doğrusu yatay ekseni
VCC değerinde keserken, aa yük doğrusu yatay ekseni VCO değerinde
kesmektedir. Bunun sebebi RAC ve RDC değerlerinin birbirinden farklı olmasıdır.
RAC<RDC dir ve VCO<VCC olacaktır. DA yük doğrusundan VCC VCEQ R DC I CQ ,
aa yük doğrusundan VCO VCEQ R AC I CQ bağıntıları elde edilir. Yükselteç
girişine aa işaret uygulandığında VCEQ gerilimi civarında en fazla VCO en az
VCEsat değerinde olabilir. Genellikle VCEQ-VCEsat ile VCO-VCEQ değerleri
birbirinden farklıdır. Bu farklılık girişten uygulanabilecek işareti sınırlamaktadır.
Kırpılmasız maksimum genlik, bu değerlerden küçük olan tarafından belirlenir.
RB direncinin değeri normal değerinden büyük seçilirse çıkış işaretinin pozitif
alternansında kırpılma, küçük seçilirse negatif alternansında kırpılma gözlenir.
Nedenini araştırınız.
Şekil 6.3. Transistörün yük doğruları
Şekil 6.2’ de verilen devrede transistörün aa eşdeğer modeli yerine konulursa
Şekil 6.4’ deki eşdeğer devre elde edilir. Bu devrenin akım ve çıkış gerilimi
'
ifadeleri i o g m V , Vo R y io eşittir. Bağıntıda bulunan (-) işareti gerilim
transfer yönü ile akım yönünün birbirine ters olmasındandır.
B
C
ib
io
Vo
gmV
π
Vg
R2
Vπ
r
E
π
Rc
Ry
RE1
Ri
Ro
Şekil 6.4. transistörün aa modelinin yerine konması ile elde edilen devre
Giriş kısmına bakarak aşağıdaki denklemler yazılır.
V r i b
Vg i b r (i b g m V )R e 0
Vb i b r (i b g mV )R e
3
io
o ’ a eşittir. Ortak emetörlü bir yükseltecin gerilim
ib
kazancı o ’a bağlıdır. Bu parametre sıcaklık, üretim ve transistörün kullanım
Akım kazancı
Ai
süresi gibi faktörlere bağlıdır. Bu yüzden devreler tasarlanırken gerilim
kazançlarının bu parametreden etkilenmemeleri sağlanmaya çalışılır. Bunun
en kolay yöntemlerinden biri RE emetör direnci kullanmaktır.
i o o i b o
Vb i b (r (1
Ri
g m V
ib
g m V
)R e ) i b (r (1 o )R e )
ib
Vb
// R B (r (1 o )R e ) // R B
ib
Bu denklemlerden yararlanarak Av gerilim kazancının bağıntısı aşağıdaki gibi
elde edilir.
R y io
R y o i b
R y o
V V
Av o o
Vg Vb i b (r (1 o )R e ) i b (r (1 o )R e ) (r (1 o )R e )
'
'
'
R y o
'
r (1 o )R e A v
o o 1 A v
Ry
(1 o )R e
'
Re
Bu bağıntılardan açıkça görülüyor ki; kazanç negatif olmaktadır. Kazancın
negatif olması ile giriş işareti ile çıkış işareti arasında 180˚ lik bir faz farkı vardır.
Diğer bir deyişle giriş pozitif yönde değişirken çıkış negatif yönde değişecektir.
RE emetör direncinin devrede bulunması ile gerilim kazancının o ’ ya olan
bağımlılığı ortadan kaldırılmıştır. Ortak emetörlü yükselteçlerin
kazançları yüksek, giriş ve çıkış dirençleri orta değerdedir.
gerilim
Bağıl Kazanç ve Desibel Tanımı:
Gerilim kazancının yada diğer kazançların yükselteçlerde logaritmik büyüklük
olarak tanımlanması bir çok durumda faydalı olur. Bu gösterilişte kazancın
modülü kullanılır. Logaritmik ölçeklendirmede esas alınan güç kazancı
Py
dB(desibel) cinsinden ifade edilir. dB cinsinden güç kazancı K G 10 log
dir.
Pi
Güç kazancına benzer bir şekilde gerilim kazancı K v (dB) 20 log K v , akım
kazancı K I (dB) 20 log K I
şeklinde ifade edilir. Bu bağıntı güç kazancının
gerilim ve gerilim kazançlarının karesi ile orantılı olmasından yararlanarak elde
edilmiştir. Giriş direnci Ri çıkış direnci Ro olan bir yükselteçte güç kazancı
4
K g (dB) K v 10 log
Ry
Ri
dir.
K I 20 log
Ro
Ri
Ri=Ry olması halinde bu üç kazanç ifadesi birbirine eşittir.
Bir Yükseltecin Frekans Karakteristiği:
Frekans eğrileri bir devrenin kazancının veya herhangi bir transfer
büyüklüğünün modülü ve fazının değişimlerini veren eğriler olarak tanımlanır.
Bir gerilim kuvvetlendiricisinin girişine küçük genlikli ve f frekanslı bir sinüzoidal
işaret uygulandığını düşünelim. işaretin genliği sabit tutularak frekansı
değiştirilirse geniş bir frekans bölgesinde çıkış gerilim genliğin de sabit kaldığı
görülür. Daha yüksek frekanslara doğru gidildiğinde çıkış genliğinde azalma
ortaya çıkar. Benzer bir azalma yükseltecin iç yapısına bağlı olarak alçak
frekanslarda meydana gelir. Çıkış işaretinin genliğinin frekansla değişimini
veren grafiğe yükseltecin genlik-frekans ya da yükselteç kazancının frekansla
değişimini veren grafiğe kazanç-frekans eğrisi denir. Frekans eğrilerinde yatay
eksen frekansa göre genellikle logaritmik olarak ölçeklendirilir. Düşey eksen
lineerdir. Kazancın sabit kaldığı bölgedeki değerinin modülünün 1 / 2 ’ sine
düştüğü frekanslara alt ve üst kesim frekansları, bu iki frekans arasında kalan
bölgeye 3dB bant genişliği denir.
Kazanç-frekans eğrileri çıkartılırken giriş işaretinin genliği sabit tutulup frekansı
değiştirilerek çıkış gözlenir. Her frekans değeri için kazanç hesaplanır.
Hesaplanan kazanç değerleri dB’ e çevrilir. Düşey eksende kazanç değerleri
yatay eksende frekans değerleri olacak şekilde eğri çizilir.
Kv(dB)
|Kv|
|Kv|/√2
3 dB
Bant
Genişliği
Şekil 6.5. Kazanç Frekans Eğrisi
ÖN HAZIRLIK
1. BC237’nin deneyde ve raporda yapacağınız teorik
kullanabileceğinizi düşündüğünüz katalog bilgilerini araştırınız.
hesaplarda
2. Şekil 6.6’ daki ortak emetörlü devrenin Ce kondansatörü devrede ve değil
iken durumlarında Vo/Vg gerilim kazancını, Ri giriş direncini ve Ro çıkış
direncini hesaplayınız. VB, VC, VE, VCE ve V0 gerilimlerini ölçüp rapordakii
tabloda hesaplanan kısmına kaydediniz.
5
DENEY NO: 6.1 ORTAK EMETÖRLÜ KUVVETLENDİRİCİ
Deney grubu ve masası:
Öğrenci Adı-Soyadı:
Öğrenci Adı-Soyadı:
No:
No:
1. Transistor ün hFE’ sini avometre yardımı ile ölçerek kaydediniz.
hFE=
2. Şekil 6.6’ daki ortak emetörlü yükselteç devresini kurunuz. Devreye giriş
işaretini uygulamadan önce CE kondansatörü devrede ve değil iken VB, VC,
VE, VCE ve V0 gerilimlerini ölçüp aşağıdaki tabloya kaydediniz. Ölçtüğünüz
değerler ile teorik hesaplamalarınızı karşılaştırıp yorumlayınız.
+ 15V
R1
Rc
87kohm
8.2kohm
C2
C1
10uF
BC237
10uF
RE1
100ohm
R2
Vg
Ry
Cy
3.3kohm
1nF
Vo
9.1kohm
RE2
1kohm
CE
470uF
Ri
Ro
Şekil 6.6. Ortak emetörlü yükselteç
Tablo 1
CE devrede varken
VB(V)
VC(V)
VE(V) VCE(V)
CE devrede yokken
Vo(V)
VB(V)
VC(V)
VE(V) VCE(V) V0(V)
Ölçüm
Hesap
3. Devrenin girişine uygulamak üzere sinyal kaynağını frekansı 5 kHz, genliği
20mV olan sinüs işaretine ayarlayınız. CE kondansatörü devrede bağlı iken Vo
çıkış gerilimini ve Vg giriş geriliminin osiloskopta aynı anda gözleyip kaydediniz.
Aynı işlemi CE kondansatörünü devreden çıkarıp tekrarlayınız. Ölçümlerinizden
yararlanarak Vo/Vg gerilim kazancını hesaplayınız ve faz farkı olup olmadığına
bakınız. Devrenin ortak emetörlü olarak çalışıp çalışmadığını yorumlayınız ve
teorik hesaplamalar ile karşılaştırınız.
6
4. Şekil 6.7’ deki düzeneği kurunuz(blok olarak verilen devre Şekil 6.6’ daki
kesikli çizgi içindeki devredir). CE kondansatörü devredeyken R potunu
devreye 0Ω olarak bağlayınız. Girişten frekansı 5kHz, genliği 20mV olan sinüs
işareti uygulayınız. Çıkış gerilimini(V0) osiloskopta gözleyip gerilim seviyesini
kaydediniz. Giriş gerilimini çıkışta bozulma ve kırpılma olmayan bir işaret elde
edene kadar attırınız. Giriş gerilimini sabit tutup R potunu attırarak çıkış
gerilimini yarıya düşürünüz. R potunu devreden çıkarıp direncini ölçüp
kaydediniz. Bu değer yükseltecin giriş direnci Ri’ ye eşittir. Nedeni araştırınız.
Ölçüm sonucunu teorik sonuçla karşılaştırıp yorumlayınız.
10 K
R
Vg
Ölçülen
50%
Şekil6.6’daki
devre
Ry
Vo
Şekil 6.7. Giriş direncinin elde edilmesi
7
Rİ
Hesaplanan
5. Şekil 6.8’ deki düzeneği kurunuz devrenin çıkışında yük direnci yokken
Girişten frekansı 5kHz genliği 20mV olan sinüs işareti uygulayınız. Çıkış
gerilimini(V0) osiloskopta gözleyiniz. Giriş gerilimini çıkışta bozulma ve kırpılma
olmayan bir işaret elde edene kadar attırıp gerilim seviyesini kaydediniz. Şekil
6.8’ de gösterildiği gibi, R potu 0Ω iken çıkışa 1kΩ seri direnç bağlayınız. Çıkış
gerilimini ölçtüğünüz gerilim seviyesinin yarısı olana kadar arttırınız. R potunu
devreden çıkarıp direncini ölçüp kaydediniz. Rpot+1KΩ yükseltecin çıkış
direnci RO’ a eşittir. Nedeni araştırınız. Ölçüm sonucunu teorik sonuçla
karşılaştırıp yorumlayınız.
1
Vg
Şekil6.6’
daki
devre
10K
1
Ölçülen
R
5 0%
Vo
2
2
2
2
Şekil 6.8. Çıkış direncinin elde edilmesi
2
2
8
1K
Ro
Hesaplanan
2.) ORTAK BAZLI KUVVETLENDİRİCİLER
DENEY MALZEMELERİ:
Dirençler : 100 kΩ, 120kΩ, 4.3kΩ, 5.6kΩ, 100Ω, 10kΩ, 500Ω’luk pot,10kΩ’luk pot
Kondansatörler : 47µF, 100µF, 220µF
Transistör : BC238 veya eşdeğeri
ÖN HAZIRLIK:
1.) BC238’in deneyde ve raporda yapacağınız teorik hesaplarda
kullanabileceğinizi düşündüğünüz katalog bilgilerini araştırınız.
2.) Şekil 6.11’de verilen ortak bazlı devrenin baz, kollektör ve emetör
uçlarındaki dc akım ve gerilimleri hesaplayıp rapordaki tabloda
hesaplanan kısmına kaydediniz.
3.) Vce gerilimini bularak devrenin hangi durumda olduğunu belirtiniz.(Aktif,
Doyum, Kesim)
GİRİŞ:
Transistörlü
temel
kuvvetlendiriciler
arasında
bulunan, basit ortak bazlı BJT
yükselteç devresi
şekil.6.9’da
gösterilmiştir. Burada baz ucu
toprağa bağlanmış olup, giriş
sinyali Cc kuplaj kondansatörü
yardımı ile emetör bacağından
uygulanır. Çıkış ucu da kollektör
bacağından alınır. Transistör sabit
bir akım kaynağı ile öngerilimlenir
ve r0 çıkış direnci de oldukça
yüksek kabul edilir.
Şekil 6.9. Basit Ortak Bazlı Kuvvetlendirici
Baz ucu ortak uçtur, hem giriş ucu hem de çıkış ucunun arasındadır. Bu
yüzden ortak bazlı yükselteç olarak isimlendirilir. Burada giriş sinyali emetör
bacağından uygulandığı için, kullanılacak en uygun küçük sinyal eşdeğer
modeli T modelidir.
Transistör yerine eşdeğer T modelini yerleştirirsek Şekil.6.10’daki eşdeğer devre
meydana gelir.
Burada r0 ihmal edebilir, çünkü r0 analizi oldukça güçleştirir. Yapılan bilgisayar
simülasyonlarından da ro direncinin ortak bazlı kuvvletlendirici performansını
etkilemediği görülmüştür.
Şekil 6.10’daki eşdeğer devre incelenecek olursa giriş direnci
Ri=re
(1)
9
re direnci oldukça küçüktür. Dolayısıyla ortak bazlı devrenin giriş direnci
küçüktür. Devrenin gerilim kazancını hesaplarsak;
V0 İ e Rc
(2)
Şekil
6.10.
Basit
ortak
bazlı
kuvvetlendiricinin
küçük
genlikli değişken işaretler
bakımından eşdeğeri
(T modeli ile)
Burada İe akımını devrenin girişinden bulursak;
Vs
Rs re
V
Rc
Av 0
Vs Rs re
İe
(3)
(4)
olarak bulunur. Yukarıdaki ifadeden de anlaşılacağı üzere devrenin kazancı,
β’nın değerine bağlı değildir. Burada kazanç daha çok Rs değerine bağlıdır.
Eğer Rs >> re ise gerilim kazancı yaklaşık olarak Rc/Rs’e eşittir. Eğer Rs direnci
de çok küçük seçilirse Av g m Rc ’dir. Ortak bazlı kuvvetlendiriciyi ortak
emetörlü kuvvetlendiriciden ayıran en önemli fark evirmeyen(noninverting)
olmasıdır, yani giriş gerilimi ile çıkış geriliminin aynı fazlı olmasıdır. Akım kazancı
da Şekil 6.10’daki eşdeğer devreden kolayca bulunabilir.
İ 0 İ e
(5)
İi
İe
olarak bulunur. Bulunan α değeri, ortak bazlı devrenin kısa devre akım kazancı
olarak ifade edilir. Ortak bazlı devrenin çıkış direnci eşdeğer devreden (Şekil
6.10) görüleceği üzere
Ai
R0 Rc
(6)
ye eşittir. Özet olarak ortak bazlı devre, çok düşük giriş direncine sahip, akım
kazancı yaklaşık olarak bir, çıkış direnci Rc olarak bulunan ve gerilim kazancı
da kaynağın direnci Rs’ e bağlı bir yükselteçtir. Çok küçük bir giriş direncine
sahip olduğundan ortak bazlı devreyi tek başına gerilim kuvvetlendirici olarak
kullanmak pek kullanışlı değildir. Çoğunlukla ortak bazlı devreyi birim kazançlı
akım yükselteci veya akım buffer’ ı olarak kullanmaktayız.
10
DENEY NO: 6.2 ORTAK BAZLI KUVVETLENDİRİCİ
Deney grubu ve masası:
Öğrenci Adı-Soyadı:
Öğrenci Adı-Soyadı:
No:
No:
R1=100kΩ, R2=120kΩ, R3=5.6kΩ, Rc=4.3kΩ, Rs=100Ω, Ry=10kΩ
C1= 220µF, C2=100µF, C3=47µF
Vcc=15V
Devreyi kurduktan sonra beslemelerini bağlarken dikkatli olunuz. Simetrik
besleme yapmayı unutmayınız.!
a) Devrenin baz,kollektör ve emetör uçlarındaki dc gerilimleri ölçüp,
tabloya kaydediniz. Vce gerilimi ölçerek transistörün hangi durumda
olduğunu belirtiniz. Çalışma noktasını belirtiniz.
Ölçülen Hesaplanan
Değerler Değerler
Ic
Ib
Ie
Vce
b) Devrenin girişine 20Sin2π1000t mV’luk işaret uygulayın. Devrenin çıkış
gerilimi(Vo) ile giriş gerilimini(Vs) aynı eksen takımı üzerinde
gözlemleyip, çiziniz. Devrenin gerilim kazancını hesaplayınız.
11
Şekil 6.11. Ortak bazlı kuvvetlendirici devresi
c) Devreyi Şekil 6.11’deki gibi kurunuz. Daha sonra devrenin girişine
uygulamış olduğunuz sinyali (Vs)’ i, çıkışta (Vo) maksimum kırpılmasız
gerilim elde edene kadar artırınız. Daha sonra devrede C1 kapasitesi
ile Rs direnci arasına 500Ω’luk potu bağlayınız. Devreye bağladığınız
500Ω’luk potu, maksimum kırpılmasız gerilimin yarısını elde edinceye
kadar yavaş yavaş artırınız. Çıkıştaki gerilimi yarıya düşüren direnç
değerini, potu devreden çıkararak ölçünüz. (Potu devre üzerinde iken
ölçmeyiniz.!!!!) Ölçülen bu değer devrenin giriş direncine eşittir.
Ölçülen
Hesaplanan
Rİ
d) Devreyi tekrar Şekil 6.11’deki hale getiriniz. Daha sonra devrenin çıkış
direncini bulmak için ‘c’ seçeneğindeki gibi çıkışta maksimum kırpılmasız
gerilim elde edene kadar giriş gerilimini artırınız. Daha sonra devrede
gösterilen C2 kapasitesi ile Ry yük direnci arasına 10kΩ’ luk potu
bağlayınız. Potu, çıkış gerilimi yarıya inene kadar artırınız. Daha sonra potu
devreden çıkarıp ölçünüz. Bulunan değer Ro çıkış direncine eşittir
Ölçülen
Hesaplanan
Ro
e) Ortak emetörlü devre ile ortak bazlı devrenin giriş direnci, çıkış direnci,
gerilim kazancı, akım kazancı ve band genişliği açısından karşılaştırıp,
yorumlayınız.
12