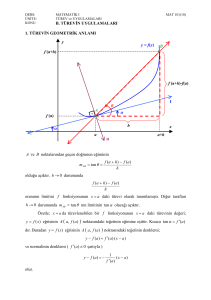
TÜREV UYGULAMALARI
• Artan ve Azalan Fonksiyonlar:
f : A R fonksiyonu verilsin.
Her x1 , x2 A ve x1 x2 için f x1 f x2
oluyorsa f ye monoton artan (azalmayan)
fonksiyon denir.
Her x1 , x2 A ve x1 x2 için f x1 f x2
oluyorsa kesin artan fonksiyon denir.
Benzer şekilde;
her x1 , x2 A ve x1 x2 için f x1 f x2
oluyorsa f ye monoton azalan (artmayan)
fonksiyon denir.
Her x1 , x2 A ve x1 x2 için f x1 f x2
oluyorsa kesin azalan fonksiyon denir.
Eğer her x a, b için f x 0 ise
fonksiyon monoton azalan, f x 0 ise kesin
azalan fonksiyondur.
Eğer her x a, b için f x 0 ise
fonksiyon monoton artan, f x 0 ise kesin
artan fonksiyondur.
Örnek: Bir malın toplam maliyet
fonksiyonu, x mal miktarı, C x bin TL olmak
üzere
C ( x) 0,5x 4 x 1400 , 0 x 200
2
toplam gelir fonksiyonu, R (x ) bin TL
olmak üzere,
R( x) 500 x 1,5 x
2
, 0 x 200
dır. Kârın artan ve azalan olduğu üretim
satış aralıklarını bulunuz.
Çözüm: Kâr, gelir ile maliyetin farkı
olduğundan K kâr fonksiyonu,
K ( x) 500 x 1,5 x 0,5 x 4 x 1400
2
2
2 x 496 x 1400
2
olur. K fonksiyonunun türevinin işaretini
incelememiz gerekiyor.
K ( x) 4 x 496 4 x 496 0
496
x
124
24
x
0
K
+
0
K
124
200
-
• Bu durumda (0,124) aralığında kâr
artmakta, (124,200) aralığında ise
azalmaktadır.
• Yerel Maksimum ve Yerel Minimum:
f : A R fonksiyonu verilsin ve x0 A için
x0 noktasını içeren uygun bir aralık I I A
olsun.
* Eğer her x I için f ( x) f ( x0 ) oluyorsa
x0 noktasına f fonksiyonunun bir yerel
maksimum noktası, f( x0) sayısına da bir yerel
maksimum değeri denir.
* Eğer her x I için f ( x) f ( x0 ) oluyorsa
x0 noktasına f fonksiyonunun bir yerel
minimum noktası, f( x0 ) sayısına da bir yerel
minimum değeri denir.
* Bir fonksiyonun yerel maksimum ve yerel
minimum noktalarına fonksiyonun ekstremum
noktaları denir.
f : a, b R fonksiyonu sürekli ve her
x a, b için türevi olan bir fonksiyon
olsun. Eğer bir x0 a, b noktası f
fonksiyonunun bir yerel ekstremum noktası
ise f ( x0 ) 0 dır.
• Türevi olan bir f fonksiyonu için f ( x) 0
koşulunu sağlayan noktalar ekstremum
noktası olmaya aday noktalardır. Böyle
noktalara kritik noktalar denir.
Örnek: f : R R , f ( x) x 3 12 x
fonksiyonunun kritik noktalarını bulalım.
f ( x) 3x 12 3x 12 0
2
2
x 4 x 2 ve x 2
2
noktaları kritik noktalardır.
Ekstremum noktaların bulunması:
1.YOL: Bir fonksiyonun ekstremum
noktalarını bulmak için türevi ve türevin
kökleri, yani kritik noktaları bulunur. Daha
sonra varsa fonksiyonun türevinin olmadığı
noktalar da belirlenip türevin işareti incelenir.
Sürekli fonksiyonun türevinin işaretinin + dan –
ye geçtiği nokta yerel maksimum noktası, -den
+ ya geçtiği nokta yerel minimum noktasıdır.
Türevin işaret değiştirmediği nokta ekstremum
nokta değildir.
Örnek:
1 5 1 4
3
f ( x) x x x 6
5
2
fonksiyonunu göz önüne alalım.
4
3
2
4
3
2
f ( x) x 2 x 3 x x 2 x 3 x 0
x ( x 1)( x 3) 0 x 0 , x 1 , x 3
2
x
f
f
+
-1
0
-
3
-
+
x=-1 yerel maksimum noktasıdır.
x=0 ekstremum nokta değildir.
x=3 yerel minimum noktasıdır.
2.YOL: f : a, b R ikinci mertebeden
sürekli türevi olan bir fonksiyon ve x0 a, b
bu fonksiyonun kritik noktası olsun.
* Eğer f x0 0 ise x 0 noktası f
fonksiyonunun bir yerel minimum noktasıdır.
*Eğer f x0 0 ise x 0 noktası f
fonksiyonunun bir yerel maksimum
noktasıdır.
Örnek: f ( x) x 4 4 x 3 4 x 2 7
fonksiyonunu göz önüne alalım.
f ( x) 4 x 3 12 x 2 8 x 4 x 3 12 x 2 8 x 0
4 x x 3x 2 0 x1 0 , x2 1 , x3 2
2
Bu noktalar fonksiyonun kritik noktalarıdır.
f x 12 x 2 24 x 8 olur. f (0) 8 0
olduğundan x=0 bir yerel minimum
noktasıdır.
f 1 12 24 8 4 0 olduğundan x=1
bir yerel maksimum noktasıdır.
f (2) 12.4 24.2 8 8 0 olduğundan
x=2 bir yerel minimum noktasıdır.
Örnek: Bir malın, x mal miktarı türünden
kâr fonksiyonu, bin TL cinsinden
x2
K ( x)
4 x 2250 , 0 x 3000
750
dir. Maksimum karın elde edildiği mal
miktarını bulunuz.
Çözüm:
x
x
K ( x)
4
4 0 x 1500
375
375
x
K
0
1500
+
3000
-
K
750
Bu üründen 1500 tane üretilip satıldığında
maksimum kâr olarak 750 bin TL elde edilir.
• BÜKEYLİK
f : a, b R ikinci mertebeden sürekli
türevi olan bir fonksiyon olsun.
* Her x a, b için f ( x) 0 ise f
fonksiyonu a, b aralığında yukarı bükey
(konveks) fonksiyondur.
* Her x a, b için f ( x) 0 ise f
fonksiyonu a, b aralığında aşağı bükey
(konkav) fonksiyondur.
* Bir fonksiyonun bükeyliğinin değiştiği
noktaya büküm noktası denir.
3
2
f
x
x
3
x
2
Örnek:
fonksiyonunu göz önüne alalım.
2
f x 3x 6 x f ( x) 6 x 6
olur. İkinci mertebeden türevin kökü x=-1
olur.
x
f
f
-1
-
-
Aşağı Bükey
o
+ +
Yukarı Bükey
• ASİMPTOTLAR
Bir eğriye, orijinden sonsuz yaklaştığımızda
teğet olan eğriye veya doğruya asimptot
denir.
1. Yatay Asimptot: y f (x) fonksiyonu
verilsin. Eğer lim f x ve lim f ( x)
x
x
limitleri var ve
lim f x b
x
ve
lim f ( x) c
x
oluyorsa y=b ve y=c doğrularına yatay
asimptot denir.
Örnek:
6 x 5x 3
f ( x) 2
3x 2 x 7
2
fonksiyonunu göz önüne alalım.
5 3
6x 2
2
6 x 5x 3
x x
lim
lim
2
7
2 2
x 3 x 2 x 7
x
3x 2
x x
5 3
6 2
x x
lim
2 olduğundan y=2
2 7
x
yatay asimptottur.
3 2
x x
2
2. Düşey Asimptot: y f (x) fonksiyonu
verilsin.
x=a için lim f x veya lim f ( x)
x a
x a
oluyorsa x=a doğrusuna fonksiyonun düşey
asimptotu denir. Bu tanıma göre bir rasyonel
fonksiyonda pay sıfırdan farklı olmak üzere
paydayı sıfır yapan değerler bize düşey
asimptotu verir.
Örnek:
x 3x 4
f x 2
x x2
2
fonksiyonunun düşey asimptotlarını bulalım.
Paydayı sıfır yapan değerler;
x x 2 0 x 1x 2 0
2
x 1 ve x 2
olur. Dolayısıyla x=-1 ve x=2 doğruları düşey
asimptottur.
• FONKSİYONLARIN GRAFİKLERİNİN
ÇİZİMİ
Bir fonksiyonun grafiğini çizmek için
aşağıdaki 7 adım takip edilir.
1.Fonksiyonun tanım kümesi bulunur.
2.Fonksiyonun belirttiği eğrinin varsa
eksenleri kestiği noktalar bulunur.
3.Eğer varsa asimptotlar bulunur.
4.Türev alınır ve işareti incelenir.
5.İkinci türev alınır ve işareti incelenir.
6.İlk beş adımda bulunanlar bir tabloda
gösterilir.
7.Altıncı adımdaki tablo kullanılarak
grafik çizilir.
Örnek: f x 2 x 15
x5
fonksiyonunun grafiğini çizelim.
1.Tanım kümesi
T R 5 ,5 5,
olur.
2. y=0 için
2 x 15
15
0 2 x 15 0 x
x5
2
olur. Dolayısıyla x eksenini kestiği nokta
15
,0 noktasıdır. x=0 için y=-3 olup y
2
eksenini kestiği nokta (0,-3) noktasıdır.
3. Verilen fonksiyon rasyonel olduğundan
paydayı sıfır yapan x=-5 düşey asimptottur.
2 x 15
2 ve
lim
x x 5
2 x 15
2
lim
x x 5
olduğundan y=2 yatay asimptottur.
4. f x
25
x 5
2
olur. Bu fonksiyon x=-5
noktasında tanımlı değildir. Dolayısıyla x=-5
hariç her yerde pozitiftir.
5. f ( x)
x
50
x 5
3
olur.
-50
- -
x 5
3
- -
- o
+ +
50
x 5
3
+ +
- -
6. İşaret tablosu;
x
f x
+ +
+ +
f (x)
+ +
- -
f x 2
2
x=-5 noktasında fonksiyonun davranışını incelemek gerekir. Pratik
olarak düşey asimptotun solundaki sonsuzun işareti bu noktanın
hemen solundaki türevin işareti ile aynı, sağındaki sonsuzun işareti ise
bu noktanın solundaki türevin işareti ile ters olur.
7. Fonksiyonun grafiği:
• BELİRSİZ HALLER
0
•
belirsizliği için L’Hospital kuralı:
0
f ve g, (a,b) açık aralığının her noktasında
türevlenebilir iki fonksiyon, ayrıca
lim f ( x) 0 ve lim g ( x) 0
xa
x a
ve (a,b) aralığındaki her x için g x 0 olsun.
Bu durumda
f x
f ( x)
L lim
L
lim
x a g ( x)
x a g ( x)
olur.
Bu kural x a , x a , x , x
olması durumunda uygulanabilir.
0
şeklinde bir belirsizlik oluyorsa bu
,
0
kural kullanılır. Aksi halde kullanılmaz.
Örnek:
x 1
lim
2
x 1 x 1
limitini hesaplayalım.
lim ( x 1) 0
x1
ve
lim x
2
x1
1 0
0
olup
belirsizliği vardır. Kuralı uygularsak:
0
x 1
1 1
lim
lim
2
2
x 1 x 1
x 1 2 x
bulunur.