Deney No:

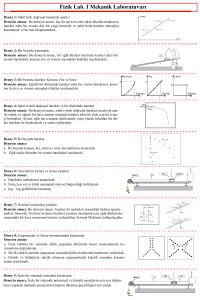
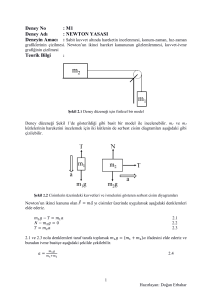
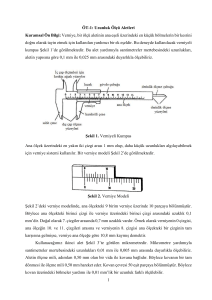
Deney No
Deney Adı
Deneyin Amacı
: M1
: ÖLÇME VE HATA HESABI
: Bazı uzunluk ölçü aletlerini tanımak ve ölçme hataları hakkında ön
bilgiler elde etmektir.
Teorik Bilgi
:
VERNİYELİ KUMPAS
Uzunluk ölçümü en eski ölçüm zorunluluklarındandır. Bu yüzden uzunluk ölçümünün en
basit metotları çok iyi bilinmektedir. Örneğin çok küçük uzunluklar için verniyenin ince kısmı
kullanılır. Verniyenin bu kısmı milimetrelik bir cetvele sahiptir ve cetvele tam dik yön de bir
ölçüm ağzına sahiptir. Yine cetvele monte edilmiş bir ikinci ölçme ağzı vardır. Eğer her iki
ölçüm ağzı temas halinde ise verniyenin sıfır işareti ile cetvelin sıfır işareti çakışık halde
bulunur.
İç yüzeylerin ölçümü için
ölçüm yüzleri
Kızak
Görev çubuğu
Verniye
Ana ölçek
çene
Derinlik ölçme
çubuğu
Derinlik ölçme
yüzeyleri
Hareketli ağız
Sabit ağız
Dış yüzeylerin ölçümü
için ölçüm yüzleri
Şekil 1.1: Verniyeli kumpas
Verniyenin iki ölçüm ağzı ile farklı ölçümler kolaylıkla yapılır. Uzun ölçüm ağzı dış boyutları
ölçmek için kullanılırken, küçük ölçüm ağzı iç boyutları ölçüm için kullanılır. Ek parçası
yardımıyla derinlik ölçümleri de kolaylıkla yapılabilir.(Şekil 1.1)
Şekil 1.2
Verniye skalası sıfır konumunda iken uzun ölçüm
işaretleri 3.9mm lik mesafeleri gösterir. İlk uzun
verniye çizgisi ile cetvelin 4mm lik çizgisi
arasındaki mesafe 0.1mm dir. İkinci uzun verniye
çizgisinin 8mm çizgisiyle arasındaki mesafe
0.2mm dir. Eğer sıfır konumundan örnek olarak
0.4mm kadar hareket ettirilirse, 4.uzun verniye
çizgisi cetvelin bir çizgisi ile çakışmalıdır. Bu
şekilde ölçümdeki kesinlik 0.1mm dir. Eğer uzun
verniye çizgilerine ek olarak kısa verniye çizgileri
kullanılırsa ölçümdeki kesinlik 2 katına
çıkar.(Şekil 1.2)
1
Ana ölçek
Şekil 1.3: Ana ölçekte okunan değer
28mm, verniyenin verdiği değerle
beraber 28,25mm okunur.
Verniye
Denemeler boyunca çeşitli boyutlar ölçülerek x sonuçları alınırsa Ortalama değer
1 n
1.1
x    xi
n i 1
(n: ölçüm sayısı)
Numune için standart sapma ise
n
1
2
1.2
Sx 
   xi  x 
n  1 i 1
Standart sapma her bir ölçüm sonucunun ortalama değerden ne kadar saptığının göstergesidir.
MİKROMETRE
Küçük kalınlıklar mikrometre ile ölçülür. Mikrometre solda ağır sabit bir kafa ile sağda
hareketli bir kafadan oluşur.(Şekil 1.4) Sırasıyla, baş tarafa tutturulmuş silindir etrafındaki
ince yüzük çevrilerek ölçüm ağzı açılır ve kapanır.
Silindir üzerindeki skala 0.5mm lik ölçüm adımlarına karşılık gelir. Ölçüm ağzı tamamen
kapalı ise skala sıfırı gösterir. Yüzük tam bir tur yaptığında, sağ ölçüm ağzı yarım milim
hareket eder. Ölçümdeki kesinlik, yüzüğün etrafına ek bir skala yerleştirilerek artırılmıştır. Bu
ek skalada 50 işaret vardır ve bu işaretler, 10 mikrometrelik ölçüm ağzı arasındaki
mesafelerin değişimine karşılık gelir. Bu nedenle ölçümdeki kesinlik 2 mikrometredir. (Şekil
1.5).
Ölçümü alınacak numune ölçüm ağzı arasına yerleştirilir. Numunenin hasar görmemesi için
yüzüğe bağlı bir vida dondurulur. Deneyde farklı kalınlıklar bir kaç kez ölçülür.
Sekil 1.4 : Mikrometre
a: Hareketsiz ölçüm ağzı
b: Hareketli ölçüm ağzı
c: Kaba skalalı silindir
d: İnce skalalı yüzük
e: Sürtünme kelepçeli vida
f: Boyunduruk
2
Şekil 1.5 : Kaba skaladaki a
mesafesinin temsili c, İnce
skaladaki a mesafesinin temsili d;
d=0.5mm+0.150mm=0.650mm
d 
1 n
 di
n i 1
1.3
(n: ölçüm sayısı)
Numune için standart sapma ise
2
1 n1
1.4
  d i  d 
n  1 i 1
ile verilir. Standart sapma her bir ölçümün ortalama değerden ne kadar saptığının
göstergesidir. Bu değer mikrometrenin vidasının okuma kesinliği ile mukayese edilir.
Sürtünme kelepçesinin ne işe yaradığı ise yumuşak bir kablonun enini bu kelepçe ile ve
kelepçesiz olarak ölçtüğümüzde anlaşılır.
s
Deneyin Yapılışı :
DIŞ BOYUTLARIN BELIRLENMESI
Ölçümü alınacak numuneyi verniyenin uzun kısmına sıkıştırınız. Dış boyut A yi milimetrik
skala yardımıyla belirleyiniz. Verniyeyi eski konumuna getirerek ölçümü tekrarlayınız.
Şekil 1.6. Uzun ölçüm ağzının kullanılarak dış boyutların ölçülmesi
Şekil 1.7. Küçük ölçüm ağzı ile iç boyutların belirlenmesi
Numuneyi küçük ağız kısmına sıkıştırınız. Milimetrik skala ile iç boyutu belirleyin ve
verniyeden de okuma yapın. Yukarıdaki adımları tekrar ederek ölçümü tekrarlayın.
3
Tablo 1.1. A boyutunun ölçüm sonuçları
i
1
2
3
4
5
Ana Ölçek
Verniye
Ai (mm)
Ortalama Değer:
Standart Sapma:
Okuma Hassasiyeti:
Tablo 1.2. B boyutun ölçüm sonuçları
i
1
2
3
4
5
Ana Ölçek
Verniye
Bi (mm)
Ortalama Değer:
Standart Sapma:
Okuma Hassasiyeti:
DERİNLİĞİN BELİRLENMESİ
Ayarı gevşetin ince uç derinliği ölçülecek numunenin tabanına değene kadar uzatılmalıdır. C
derinliğini milimetrik skala yardımıyla ve verniye yardımıyla belirleyiniz. Ve ölçümleri
tekrarlayınız.
Şekil 1.8. Uç kısım yardımıyla derinliğin belirlenmesi
4
Tablo 1.3. C boyutun ölçüm sonuçları
i
1
2
3
4
5
Ana Ölçek
Verniye
Ci (mm)
Ortalama Değer:
Standart Sapma:
Okuma Hassasiyeti:
Tablo 1.4. Alüminyum tel için ölçüm sonuçları
i
1
2
3
4
5
Kaba skala
İnce skala
di (μm)
Ortalama Değer:
Standart Sapma:
Okuma Hassasiyeti:
di (μm)
Ortalama Değer:
Standart Sapma:
Okuma Hassasiyeti:
Tablo 1.5. Bakır tel için ölçüm sonuçları
i
1
2
3
4
5
Kaba skala
İnce skala
5
Deney No
Deney Adı
Deneyin Amacı
: M2
: NEWTON YASASI
: Konum-zaman, hız-zaman grafikleri ile kütle, ivme ve kuvvet
arasındaki ilişkinin düzgün ivmeli hareket için, doğru bir hat üzerinde hava rayı sistemi
yardımıyla belirlenmesi.
Teorik Bilgi
:
Kütlenin m ile ve uygulanan kuvvetin F ile tanımlandığı Newton’ un hareket denklemi
aşağıda verilmiştir.

2.1
F  m.a
burada,

 d 2r
2.2
a 2
dt
ivmedir. Sabit kuvvet uygulanarak elde edilen v hızının, verilen zamanın bir fonksiyonu
olarak ifade edildiği eşitlik,


F
2.3
v (t )  t
m
için,

v (0)  0
kabul edildiğinde,


v (0)  0 ; r (0)  0

kütle merkezinin konumu, r ,


1F 2
2.4
r (t ) 
.t
2m
Mevcut durumda hareket boyutsuzdur ve m1 ağırlığının oluşturduğu kuvvet,


F  m1 . g  m1 .g
Burada g yer çekimi ivmesidir. Eğer kızağın toplam kütlesi m2 ise, hareketin denklemi,
m2  m1 . a  m1 .g ;
a
m1
g
m1  m2
2.5
Tablo 2.1: Sabit ivme altında, düz bir hat boyunca hareketin kinematik denklemleri
Denklem
Denklem tarafından verilen bilgi
v xf  v xi  a x t
Zamanın bir fonksiyonu olarak hız
1
(v xi  v xf )t
2
1
x f  xi  v xi t  a x t 2
2
x f  xi 
v xf  v xi  2a x ( x f  xi )
2
6
2
Hız ve zamanın fonksiyonu olarak yer değiştirme
Zamanın fonksiyonu olarak yer değiştirme
Yer değiştirmenin fonksiyonu olarak hız
Deneyin Yapılışı :
Deney düzeneği Şekil 2.1’de gösterilmiştir.
1.
Şekil 2.1: Düzgün hızlanan hareketin incelenmesi için deney düzeneği
2.
Kompresörün raya üflediği havayı, kızağın sürtünmesiz hareket etmesini sağlayacak
şekilde ayarlayınız.
3.
Kompresör çalıştırıldığında, kızak hareket etmeyecek şekilde denge vidası ayarlanır.
4.
Dört adet ışık bariyerinin pozisyonları yaklaşık olarak eşit aralıklarda olmalıdır.
5.
Son ışık bariyeri, ivmelenen kütlenin zemine çarpmadan önce geçeceği şekilde
yerleştirilmelidir.
6.
Ağırlık tutucuya 10g’lık kütle yerleştirin (ağırlık tutucunun 1g olduğunu hatırlayınız.).
Başlangıç pozisyonundaki kenardan ışık bariyerlerine kadar alınan yolları ( s1 , s 2 , s3 , s 4 )
sırasıyla ölçünüz. Bütün ölçümleri ışık bariyerlerinin konumlarını değiştirmeden yapınız ve
Tablo 2.2’ye kaydediniz.
Tablo 2.2
m1 ( g ) m2 ( g )
10
210
10
210
10
210
t1 ( s)
t 2 ( s)
t 3 ( s)
t 4 ( s)
s1 (m)
s 2 (m)
s3 (m)
s 4 (m)
Ortalama:
Alınan dört s1 , s 2 , s3 , s 4 mesafeleri için gereken t1 , t 2 , t 3 , t 4 sürelerinin kronometre ile
ölçülmesinden sonra, hızları Tablo 1’den yararlanarak hesaplayınız ve Tablo 2.3’e
kaydediniz.
7.
v1  ………………………………………………………………………………………………………
……………………………………………………………………………………………………………
……………………………………………………………………………………………
7
v2  ………………………………………………………………………………………………………
……………………………………………………………………………………………………………
……………………………………………………………………………………………
v3  ………………………………………………………………………………………………………
……………………………………………………………………………………………………………
……………………………………………………………………………………………
v4  ………………………………………………………………………………………………………
……………………………………………………………………………………………………………
……………………………………………………………………………………………
Tablo 2.3
v1 (m / s)
v 2 (m / s )
v3 ( m / s )
v 4 (m / s )
8.
Kızağın üzerindeki yuvalara ağırlık eklenerek kütlesi değiştirilebilir. Ağırlıklar
simetrik olarak yerleştirilmelidir. Formül 5 yardımıyla, aşağıda verilen ağırlıklar için ivme
değerini hesaplayınız. Sonuçları Tablo 2.4’ e yazarak, a (m / s 2 )  (m1  m2 ) g grafiğini
çiziniz. ( m1 ; ağırlık tutucunun kütlesi ve m2 kızağın toplam kütlesidir. m1 =10g
a1 =………………………………………………………………………………………….…
…………………………………………………………………………………………………
…………………………………………………………………………………………
a 2 =………………………………………………………………………………………………
…………………………………………………………………………………………………
………………………………………………………………………………………
a 3 =………………………………………………………………………………………….…
…………………………………………………………………………………………………
…………………………………………………………………………………………
a 4 =………………………………………………………………………………………………
…………………………………………………………………………………………………
………………………………………………………………………………………
Tablo 2.4
m1 ( g )
m2 ( g )
10
210
10
250
10
310
a(m / s 2 )
9.
Kuvvetin bir fonksiyonu olarak ivme hesaplandığında toplam kütle sabit kalmalıdır.
Ağırlık tutucu üzerine 4 g’ lık kütleyi yerleştiriniz (Ağırlık tutucunun kütlesinin 1 g olduğunu
hatırlayınız.). Sırasıyla 2 g’ lık kütleleri ağırlık tutucuya yerleştirerek aşağıdaki tablodaki
değerleri alınız ve ( m / s 2 )  F ( N ) grafiğini çiziniz.
a1 =………………………………………………………………………………………………
…………………………………………………………………………………………………
………………………………………………………………………………………
8
a 2 =………………………………………………………………………………………………
…………………………………………………………………………………………………
………………………………………………………………………………………
a 3 =………………………………………………………………………………………………
…………………………………………………………………………………………………
………………………………………………………………………………………
a 4 =………………………………………………………………………………………………
…………………………………………………………………………………………………
………………………………………………………………………………………
Tablo 2.5
m1 ( g )
F  m1  g ( N )
s 4 (m)
t 4 ( s)
a(m / s 2 )
4
6
8
10
Sorular
1.
2.
3.
:
Newton’un hareket yasaları nelerdir?
Bu deney düzeneğinde Newton’ un tüm hareket yasaları gözlenmiş midir?
Deney sonuçları elde edildiğinde hesaplanan hata oranının değeri nelere bağlıdır?
9
Deney No
Deneyin Adı
Deneyin Amacı
: M3
: İKİ BOYUTTA ESNEK ÇARPIŞMA
Teorik Bilgi
:
: İki boyutta esnek çarpışmada, enerji ve momentum korunum
bağıntılarını incelemek, momentumun vektörel, enerjini skaler bir büyüklük olduğunu
deneysel olarak göstermektir.
Mekanik Enerjinin Korunumu
Enerji skaler bir büyüklük olup kinetik enerji ve potansiyel enerji olarak ikiye ayrılır.
Aşağıda, U ile potansiyel, K ile kinetik enerji gösterilmektedir. Etkileşmeden önceki durumlar
ilk, sonrakiler ise son alt indisi ile gösterilmiştir. İş–enerji teoremine göre, bir cismin kinetik
enerjisindeki değişiklik, cismin üzerindeki net kuvvetin yaptığı işe eşittir.
3.1
K son  Kilk  W
Cismin üzerinde yalnız korunumlu kuvvetlerin iş yaptığın düşünelim. Korunumlu bir
kuvvetin yaptığı iş, yoldan bağımsız olup, potansiyel enerjideki değişikliğin zıt işaretlisine
eşittir. Bu sonuçları birleştirirsek,
3.2
K son  Kilk  W  U son  Uilk 
elde ederiz. Bu son ifade yeniden düzenlenirse,
3.3
K son  U son  Kilk  Uilk
elde edilir. Burada, sol taraftaki terim, çarpışmadan sonraki toplam enerji, sağ taraftaki terim
ise çarpışmadan önceki toplam enerjidir. Yani; E  K  U olmak üzere;
3.4
Eson  Eilk
elde edilir. Mekanik enerji korunmaktadır, çünkü iş yapan kuvvetler hep korunumlu olup
yapılan net iş potansiyel enerjideki değişikliğin zıt işaretlisine eşittir. Eğer yalnız korunumlu
kuvvetler iş yapmakta ise, sistemin mekanik enerjisi korunur. 3.4 denklemi 1,2 ya da 3
boyuttaki bir sistemin mekanik enerjisinin korunumunu ifade etmektedir. Bu bağıntı, cismin
hızı ile konumunu bağlamaktadır. Cismin hareketi boyunca hem kinetik hem de potansiyel
enerji değişir ama toplamları değişmez. Enerjinin korunumu yasası, yalıtılmış bir sistemde
toplam enerjinin korunduğunu söyler.
Momentumun Korunumu


Kütlesi m ve hızı v olan bir parçacığın P momentumu, kütle ile hız vektörünün
çarpımı olarak tanımlanır.


P  mv
3.5
Momentum, vektörel bir niceliktir. Newton’un ikinci yasası, aşağıdaki şekilde yazılabilir.
 dP
F
3.6
dt
3.5 denkleminin zamana göre türevi alınırsa (cisim, ışık hızına yakın hızlarda hareket
etmiyorsa m sabittir
 ), 
dP
dv

m
 ma
3.7
dt
dt
elde edilir. Bir parçacık sistemi için Newton’un ikinci yasası,


3.8
 Fd  ma
olur. Bu sonuçları birleştirirsek,


dP
3.9
 Fd  dt
elde ederiz. Bu da, bir parçacıklar sistemi için sistemin P momentumu cinsinden yazılmış
Newton` un ikinci yasasıdır. Bu sistemin momentumunun değişme hızı, sisteme uygulanan
10
net dış kuvvete eşittir. Üstüne etkiyen dış kuvvet sıfır olan bir sistem düşünelim. O zaman,
aşağıdaki eşitlik elde edilir.

dP
3.10
0
dt
Bu, momentumun zamanla değişimi sıfırdır veya momentum zamanla değişmiyordur
demektir. Yani, bu sistem için herhangi bir başlangıç anındaki momentum ile herhangi bir
bitiş anındaki momentum aynıdır. Diğer bir deyişle sistemin momentumu korunur.
3.11
Pilk  Pson
Deneyin Yapılışı :
Deney yapacağımız düzenekte, sürtünmeyi mümkün olduğunca en az hale getirmek
için bir adet hava masası kullanmaktadır. Masanın üzerinde bir adet karbon kâğıdı ve onun
üzerinde parçacıkların yörüngelerini kıvılcım üreteci sayesinde işaretleyebileceğimiz bir
beyaz kâğıt serilidir.
1. Hava masası üzerinde hava pompası ve kıvılcım üretecine bağlı olan hortumlara iki adet
kızak takılıdır. Kızaklardan bir tanesini masanın merkezine koyarak koordinat merkezini
oluşturun. Diğer kızağa da istediğimiz herhangi bir açıdan, ıstaka ile vurarak iki kızağın esnek
çarpışma yapmasını sağlayın. Dikkat edeceğiniz nokta, hareketi başlattığınız an kıvılcım
üretecinin pedalına basmak ve hareket devam ettiği sürece pedalı basılı tutmaktır. Bu şekilde
kâğıdın arka yüzüne hareketlerin yörüngeleri iz bırakacaktır.
2. Yörüngelerin izlerine göre koordinat merkezlerini belirleyin. Hareketin hangi eksen ile ne
kadar açı yaptığına dikkat edin. Momentum ve kinetik enerji bağıntıları için kütle ve hız
değerlerine ihtiyacınız olacaktır. Kütle değerlerini, terazide tartarak bulun. Hızlar için, mesafe
11
ve zaman değerlerinin belirlenmesi gereklidir. Mesafeleri cetvel ile ölçün. Zamanları ise,
ölçtüğünüz mesafedeki iz sayılarını kıvılcım üreteci üzerindeki periyot değeriyle çarparak
bulabilirsiniz. İki kütlenin bir düzlemde esnek çarpışma yapması sonucu, dikey ve yatay
eksenlerdeki momentum ve enerji korunum ifadeleri aşağıdaki şekilde ifade edilir. Cetveli
kullanarak size gereken trigonometrik ifadeleri elde edebilirsiniz.
Momentum – yatay ; m1v1x _ ilk  m2v2 x _ ilk  m1v1' x _ son  m2v2' x _ son
3.12
Momentum - düşey ; m1v1 y _ ilk  m2v2 y _ ilk  m1v1' y _ son  m2v2' y _ son
3.13
1
1
1
1
3.14
m1v12ilk  m2v22ilk  m1v1'2son  m2v2'2son
2
2
2
2
3. Yukarıdaki enerji ve momentum korunum bağıntılarını deneysel olarak sağlayınız. Eğer
değerlerinizde herhangi bir hata varsa bu hatanın deneyde nereden kaynaklanmış olabileceğini
tartışınız.
4. Yukarıdaki enerji korunum bağıntılarında neden potansiyel enerji ifadesi yer
almamaktadır? Açıklayınız.
5. Enerji ile momentum arasındaki en temel matematiksel ifade farkı nedir? Yukarıdaki
denklemleri inceleyerek açıklayınız.
kg
m1 
kg
m2 
Çarpışmadan
önce
x(m)
y(m)
vx(m/s)
vy(m/s)
v(m/s)
Px(kgm/s)
vx(m/s)
vy(m/s)
v(m/s)
Px(kgm/s)
Py(kgm/s)
P(kg/s)
E(kgm2/s2)
m1
m2
Çarpışmadan
sonra
m1
m2
12
x(m)
y(m)
Py(kgm/s)
P(kg/s)
E(kgm2/s2)
Deney no
Deneyin adı
Deneyin amacı
: M4
: EYLEMSİZLİK MOMENTİ VE AÇISAL İVMELENME
: Dönme hareketinde eylemsizlik momentinin ne demek olduğunu ve
nelere bağlı olduğunu deneysel olarak gözlemlemek.
Teorik bilgi
:
Günlük yaşamdan büyük kütleli cisimlerin zor hareket ettirildiğini ve onları hareket
ettirebilmek için diğer hafif cisimlere oranla daha fazla enerji harcamamız gerektiğini
biliyoruz. Bu basit gözlem bize kütlenin en genel anlamda cismin harekete karşı gösterdiği
isteksizlik yani direnç olduğunu söylemektedir. Doğada cisimler dönme ve öteleme (bir doğru
boyunca yapılan hareket) hareketi yapabilirler.
Şimdi bir kütleyi F kuvveti ile a kadar ivmelendirmeye çalıştığınızı düşünün. Cismin
kütlesine göre zorlanır veya zorlanmazsınız. Zorlanmanızın kaynağı bu harekete direnç
gösteren kütledir. Cisim bu kuvvete rağmen eylemsiz kalmak istemektedir. Bu nedenle lineer
kinetikte kütle, eylemsizliğin bir göstergesi olarak tanımlanır. Newton’da kütle için bu
nedenle eylemsizlik ifadesini kullanmıştır.
Aynı kütleyi bir eksen etrafında veya kendi kütle merkezi etrafında döndürmeye çalışın.
Cismi döndürmeye çalıştığınız eksene ve kütlesine bağlı olarak cismin dönmeye de karşı bir
direnç gösterdiğini görürsünüz. Örneğin ağır bir çubuğu kütle merkezi etrafında döndürmekle,
en uç kenarından döndürmek için harcayacağınız çaba aynı olmayacaktır. Öyleyse cisimler
lineer (öteleme) harekete gösterdikleri isteksizliği dönme hareketinde de gösteriyor diyebilir
miyiz?
İşte dönmedeki bu zorluğa eylemsizlik momenti diyoruz. Lineer hareketteki dönmeye
karşı zorluk yalnızca kütleye bağlı olarak ifade edilirken, dönme (rotasyon) hareketinde
cismin göstereceği direnç yani cismin eylemsizlik momenti seçilen eksene ve kütleye aynı
anda bağlıdır. Rotasyonel (dönme) hareketi için hareket kanunu;
τ= Iα
4.1
olarak ifade edilir. Burada τ döndürme kuvveti yani tork olup birimi Newton.metre (SI) dır.
Açısal ivmenin birimi ise radyan/sn2’dir. Eylemsizlik momenti I’nın birimi ise kg.m2’dir.
Eylemsizlik momenti birçok kütleden oluşmuş bir sistem için en genel şekilde şöyle formüle
edilebilir.
I=  mi .ri 2
4.2
Bazı geometrik cisimler için hesaplanmış teorik eylemsizlik momenti 4.2 denklemi
yardımı ile kütle merkezi etrafında bulunan) ifadeleri şöyledir.
a) M kütleli r yarıçaplı düzgün bir disk veya dolu silindir;
1
Ikm= mr 2
2
b) M kütleli L uzunluklu çubuk;
1
Ikm= mL2
12
c) M kütleli dönme ekseninden r mesafe uzaklıkta noktasal kütle;
Ikm= mr2
d) Dolu küre;
2
Ikm = mr2
5
e) İnce küresel kabuk;
2
Ikm= mr2
3
f) Silindirik kabuk;
Ikm= mr2
13
Deneyin yapılışı :
Şekil 4.1. Deney düzeneği
Şekil 4.2.
Deney düzeneği masa üzerinde şekilde ki gibi kurulu haldedir. Bir disk, iki silindir, bir
küre ve bir çubuk için ayrı ayrı deneysel ve teorik eylemsizlik momentleri hesaplanır.
Deneyde şu işlemler takip edilir.
1) Bunun için ölçümü alınacak geometrik cisim dönme eksenine oturtulur.
2) Cisimler üzerinde bulunan siyah renkli şerit ışık bariyerinin cismi görmesini ve böylece
cismin dönme periyodunu okumasını sağlar.
3) Kütle henüz durgunken ışık bariyerinin bu şeride baktığından emin olun. Işık bariyerini
periyot modunda çalıştırın. Aynı cismi farklı açılardan bırakıp ışık bariyerinde
okuduğunuz değerlerin ortalamasını alın. Bu değer o cismin periyodu olacaktır.
Periyot ile cismin z ekseni etrafındaki eylemsizlik momenti arasındaki ilişki şu şekildedir.
14
Iz
olur.
4.3
D
Burada D deneydeki düzenekten kaynaklanan açısal yer değiştirme faktörüdür.
Büyüklüğünü dört değişik burma açısı (45,90, 135, 180) ında eşitlik 4.3 kullanarak
hesaplanacaktır. (I-T2 grafiğinden eğim hesaplanarak)
4) Cismin periyodunu ışık bariyerinden okuyup denklem 4.3 yardımıyla yukarıda anlatılan
işlemleri sırayla küre, disk, silindir, demir silindir, demir disk, demir çubuk için
tekrarlayın.
5) Demir çubuğun üzerinde bulunan silindirik kütlerlin de kendilerine ait eylemsizlik
momentleri vardır. Önce demir çubuktan kütleleri çıkarın ve çubuğun eylemsizlik
momentini Içubuk bulun. Daha sonra silindirik kütleleri çubuğa yerleştirin. Her bir silindirik
kütlenin dönme ekseninden eşit mesafede bulunmasına dikkat edin. Çubuk + kütlelerden
oluşmuş sistemin periyodunu 5 kez ölçerek ortalama bir değer alın ve eşitlik 4.3 yardımı
ile tüm sistemin (Içubuk+I kütleler) eylemsizlik momentini bulun.
Isistem= Içubuk+Ikütleler= (M1+M2)r2+ Içubuk
4.4
T= 2 
Sistemin eylemsizlik momentinin r2’ye göre grafiğini çizin. Bu grafik y=mx+b eşitliğine
uyan bir grafik oluyor mu? Grafiğin eğimi neyi vermelidir. Bu değer gözlemlerinizle
uyuşuyor mu?
Yalnızca silindirik kütlelerin o dönme ekseni etrafındaki eylemsizlik momentini bulmak
için ne yaparsınız?
6) Şimdi çubuktaki silindirik kütlelerin her birini dönme ekseninden farklı mesafelere
yerleştirin. Şekil 4.2’ye bakınız. Bu sistemin deneysel olarak eylemsizlik momentini
hesaplayın. Teorik olarak Ikütleler= M1r12+M2r22 formülü ile hesaplanmalıdır. Neden?
7) A_Üzerinde delikler bulunan büyük diski kütle merkezinden döndürerek eylemsizlik
momentini bulun. Daha sonra aynı diski kütle merkezinden farklı noktalarda döndürerek
eylemsizlik momentini bulun. Bulduğunuz sonuçlar aynı mı? Neden? Eylemsizlik
momenti döndürme eksenine göre değişiyor mu?
B_Diski kütle merkezinden farklı bir nokta etrafında döndürdüğünüzde teorik olarak
eylemsizlik momentini nasıl hesaplarsınız? Yukarıda verilen formüller cismin kütle
merkezi etrafında döndürüldüğünü varsayıyordu.
8) Her bir geometrik cisim için bulduğunuz deneysel eylemsizlik momentleri değerlerini
yukarıda verilen formülleri kullanarak teorik değerlerle karşılaştırın.
9) Teorik hesaplama için gerekli her bir cismin kütle değerleri şöyledir. Uzunlukları ise
deney sırasında kendiniz ölçerek kaydedin.
10) Sonuçları cisimlerin geometrisine ve eksen uzaklıklarına bağlı olarak yorumlayın.
Sorular
:
1) Bir buz patencisi bir ayağını yana doğru açarak kendi etrafında döndüğü zaman mı daha
çok açısal hız kazanır yoksa ayağının başına doğru kaldırıp birleştirdiği zaman
mı?(Eylemsizlik momenti ile açısal ivmelenme arasındaki ilişkiyi araştırarak
cevaplayınız.)
2) Eylemsizlik momentini daha başka nasıl ölçerdiniz. Bir deney setini planlayınız.
3) Bir galakside bulunan binlerce sistemde o galaksi içersinde dönmektedir. Böyle çok
sayıda kütlenin bulunduğu durumlarda her bir kütlenin ayrı ayrı eylemsizlik momentini
bulmak yerine nasıl bir yol izlenebilir? (Kütle merkezi kavramını hatırlayınız)
15
Deney No
Deneyin Adı
Deneyin Amacı
: M5
: ESNEKLİK MODÜLÜ
:Düzgün alüminyum, çelik, pirinç ve bakır çubukların eğilme miktarını;
buna bağlı olarak esneklik modülünü
1. Kuvvetin,
2. Sabit kuvvet altında kalınlığın,
3. Sabit kuvvet altında genişliğin,
4. Sabit kuvvet altında çubukları tutan sabit noktalar arasındaki mesafenin bir fonksiyonu
olarak bulmak
Teorik Bilgi
:
Eğer bir katının sürekli olduğu düşünülürse, r0 ve r katının deforme olmuş ve deforme
olmamış durumları için bir P noktası vektörlerini göstersin. Küçük yer değiştirmeler
vektörleri;
  
5.1
u  r  r0  u1 , u 2 , u3 
bükülme tensörü d̂ ;
u i u k
5.2

xk xi
Köşeleri yüzey koordinatlarına paralel olarak yerleştirilmiş bir katının birim hacmine etkiyen

dF kuvveti, tˆ gerilme tensörü olarak ifade edilir. Bu sayede, her bir dA birim alandaki stres,


p normal doğrultudaki birim vektör e ’ye bağlı olarak şu şekilde verilir.

dF
5.3
p
dA
 
5.4
p  e  ˆ
d ik 
Hooke’s kanunundan d̂ ile ˆ arasındaki bağıntı;
 ik   l ,m cikl ,m d lm
5.5
Elastik bir katı için ĉ tensörü simetrik olduğundan, 81 matris elemanından 21 tanesi kalır. Bu
sayı izotropik elastik katılar için 2’ye düşer. Bir tanesi esneklik modülü E, diğeri ya sıkışma
modülü G ya da Poisson oranı  ’dır.
 11 
E 

 d11 
d11  d 22  d 33 
1  
1  2

(1)*
1 E
d12
2 1 
(1)* için yazılanlar aynı şekilde  22 , 33 , 13 , 23 için de yazılabilir. Eğer kuvvet tek bir
doğrultuda uygulanıyorsa;
 22   33  0
(2)*
sonuç olarak  11  Ed 11 elde edilir.
 12  Gd12 
16
Şekil 5.1:Çubuğun bükülmesi
b uzunluğunda, a genişliğinde bir çubuk her iki ucundan tutturulursa (L uzunluğu kadar ayrı),
çubuğun merkezine bir Fy kuvveti uygulanırsa çubuk tıpkı ortadan tutturulmuş bir çubuk gibi
davranır. Çubuğun tutturulma (uç) noktaları birbirine zıt yönde olmak üzere Fy / 2 ’lik bir
kuvvete maruz kalır.
Bükülme  ’yı esneklik modülü E’nin fonksiyonu olarak yazmak istersek öncelikle
birim hacim elemanını düşünelim;
dV  d x  a  b
5.6
Bu birim elemanın üst katmanı bükülme sonucu kısalır, alt katman ise uzar. Merkez noktası
değişmeden kalır.
Şekil 5.1, I ve II bükümden önce bu kısımları göstermektedir.
Şekil 5.1’de verilen sembolleri kullanarak şu bulunur:
5.7
d  x  d  2x / b
*
dl ’lik bir genişlemeyi meydana getiren dFx elastik kuvveti, (1) ’a göre şu şekilde yazılır;
dFx
dl
5.8
E
ds
dx
Burada ds  a  dy esneyen tabakanın alanıdır. Bu kuvvet denklem 5.9’daki gibi bir tork
oluşturur.
2 Ea 2
5.9
dTz  y  dFx 
y dy
b  dx
Elastik kuvvetler tarafından oluşturulan bu torkların toplamı, dış kuvvet Fy / 2 tarafından
oluşturulan torka eşit olmalıdır.
Eab 2 Fy

x
5.10
6d x
2
buradan
6 Fy x 2
d 
dx
5.11
Eab 3
17
elde edilir. (11) ifadesinin x’e göre integrali alınırsa; toplam bükülme şu şekilde ifade edilir;
3
1  L  1 Fy
5.12
    
4 b  a E
Farklı malzemelerin ölçülen esneklik modülleri boyutlarına bağlı olarak Tablo 5.1’de
verilmiştir.
Ebat (mm)
E (N∙m-2)
Çelik
10  1,5
2.059∙1011
Çelik
10  2
2.063∙1011
Çelik
10  3
2.171∙1011
Çelik
15  1,5
2.204∙1011
Çelik
20  1,5
2.111∙1011
Alüminyum
10  2
6.702∙1010
Pirinç
10  2
9.222∙1010
Malzeme
Tablo 5.1:Farklı malzemeler için esneklik modülleri
Deneyin Yapılışı :
Deneyler uzunlukları aynı, genişlik ve kalınlıkları farklı olan beş çelik çubuk ile
yapılacaktır. Deneyde merkezden uygulanan bir kuvvet ile çubukların bükülmesi sağlanır.
Esneklik modülü bu bükülmeden ve çubuğun geometrik verilerinden hesaplanır. Deney
düzeneği Şekil 5.2’dekine benzer bir şekilde hazırlanır.
Şekil 5.2: Esneklik modülünün belirlenmesi için kullanılan deney düzeneği
18
Adımlar;
1- Düzgün çubuk iki ucundan tutturulur. Hassas gösterge, askı ve mil ile çelik üzerine
yerleştirilir.
2- Çubuklar esnek olduğundan kuvvet uygulama sonucu malzemenin bükülmesi ile
kuvvetin geri alınması ile geri gelme aynı anlamı ifade edecektir. Sistemin hassasiyeti
açısından uygulamada kolaylık için ikinci durumu tercih edeceğiz. Bunun için
öncelikle askıya kütlelerin tamamı yerleştirilir.
3- Ardından her bir kütlenin teker teker sistemden alınması ile hassas göstergedeki
durum değişikliği Tablo 5.2’ye kaydedilir.
Tablo 5.2- Deneysel Veriler
10mm  1,5mm Çelik için
10mm  2mm Çelik için
No
Kuvvet F (N)
Bükülme λ (mm)
No
1
1
2
2
3
3
4
4
5
5
No
10mm  3mm Çelik için
Kuvvet F (N)
Bükülme λ (mm)
No
1
1
2
2
3
3
4
4
5
5
No
Kuvvet F (N)
Bükülme λ (mm)
15mm  1,5mm Çelik için
Kuvvet F (N)
Bükülme λ (mm)
20mm  1,5mm Çelik için
Kuvvet F (N)
Bükülme λ (mm)
1
2
3
4
5
19
Deneyin Analizi
a) Çubukların bükülmesini kuvvetin fonksiyonu olarak belirlemek için, verilerini
aldığınız her bir tablo için grafik kağıdına bükülme-kuvvet grafikleri çiziniz.
b) Çelik için sabit kuvvet altında bükülmeyi kalınlığın fonksiyonu olarak belirlemek için
Tablo 5.2 ye göre aşağıdaki tabloyu doldurarak grafik kağıdına bükülme-kalınlık
grafiğini çiziniz.
No
Kalınlık b (mm) Bükülme λ (mm)
1
2
3
c) Çelik için sabit kuvvet altında bükülmeyi farklı genişliklerin fonksiyonu olarak
bulmak için aynı işlemleri yapınız. Grafik kağıdına bükülme-genişlik grafiği
çiziniz.
No
Genişlik a (mm)
Bükülme λ (mm)
1
2
3
d) Her bir malzeme için “ortalama bükülme ( 0 ) ” değerlerinden “Esneklik modüllerini
(E) ” hesaplayınız. (Formül 5.12)
e) Her bir malzeme için Tablo 5.1’deki verilere göre hata hesabını yapınız.
DeneyselDeğer  TeorikDeğer
100 )
(Hata hesabı nasıl yapılır? Formül: Hata% 
TeorikDeğer
f) Deneyde öğrendiklerinize dair yorumunuzu; “hesaplar, hatalar, grafikler ve neler
öğrendiğimiz hakkında” yazınız. Hiçbir deney (olumlu ya da olumsuz) asla sonuçsuz
bırakılmamalıdır. Hata sebepleri, gözlenenlerin ve diğer sonuçların yorumu muhakkak
yapılmalıdır.
NOT: Her ne kadar teori kısmında toplam kuvvetin=kütleler+hassas gösterge olduğu
belirtilmiş olsa da (bu çok iyi sonuçlar için kullanılmalı) deneysel süreçte formülde yalnızca
Fy alınmış. Yani yalnızca kütlelerden gelen katkı önemsenmiş, ölçümler buna göre yapılmış
ve yine aynı 5.12 formülüne göre esneklik modülü bulunmuştur.
Sorular
:
1. Hooke kanununu anlatınız.
2. Esnek ve esnek olmayan bozulmayı anlatınız. Hooke kanunu hangisi için geçerlidir?
3. Young modülü nedir? Esneklik modülü ile arasındaki farkı belirtiniz.
20
Deney No
Deney Adı
Deneyin Amacı
Teorik Bilgi
: M6
: BASİT SARKAÇ
: Basit sarkaç kullanarak yer çekimi ivmesini(g) belirlemek
:
Kütle merkezinden geçmeyen bir eksen etrafında salınım yapan katı bir cisim basit
sarkaç olarak tanımlanır. Böyle bir sarkaç denge konumundan küçük bir Ф açısı kadar
ayrılarak serbest bırakılırsa salınım hareketi yapar (Şekil 6.1).
Şekil 1’e göre enerji eşitliği;
l2(
d
)  2 gl (1  cos  )  Ec  sabit
dt
6.1
Şekil 6.1: Basit sarkaç ve hareketi
 ‘nin maksimum değeri için açısal hız sıfırdır ve    olur.
Bu durumda;
6.2
E0  2 gl (1  cos  )
olur.6.1 nolu denklemden ;

T
l
d
6.3


4
g 0 (cos   cos  )

k  sin( ) dönüşümü uygulandığında (Birinci dereceden eliptik integral çözümünden)
2
periyot;

l 2
d
l
4
K (k )

2
2
g 0 1  k sin 
g
bulunur. K(k) için seriye açıldığında;
l  1 2

T  2
 ......
1  sin
g 4
2

elde edilir.  ’nın küçük değerleri için;
l
T  2
g
olur.  ’nın büyük değerleri için T  ‘ya bağlıdır.
T 4
6.4
6.5
6.6
21
Deneyin Yapılışı :
1. Deney düzeneği şekilde gösterilmiştir.
2- Deneyi büyük çelik top için uygulayınız.
3- Çelik topa bağlanan ipin serbest ucu yukarıda bulunan kıskaça tutturulur. Yeni bir
ip bağlanmışsa top serbest bırakılarak ipin yeterince uzaması sağlanır.
4- Sarkacın boyunu deneyden önce ve sonra ölçünüz(Topun yarıçapı eklenmelidir).
5- Zaman ölçerin anahtar konumu soldan üçüncü olmalıdır.
6- Tepe açısını yaklaşık 5 0 olacak şekilde ayarlayınız ve topu bırakınız.
7- Zaman ölçerde okunan değer periyottur. Birden çok ölçüm yaparak ortalamasını alınız.
8- Dört farklı uzunlukta ip için periyodu ölçünüz ve kaydediniz.
Uzunluk
T(80 cm)
T(60 cm)
T(40 cm)
T(20cm)
1. Ölçüm
2. Ölçüm
3. Ölçüm
Ortalama
Tablo 6.1 Büyük top için periyot-sarkaç uzunluğu tablosu
9- Her bir periyot için yer çekimi ivmesini (g) hesaplayınız. Sonuçları tabloya yerleştiriniz.
g(20)=…………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
g(40)=…………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
g(60)=…………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
g(80)=…………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
22
Büyük Top
T(s)
g(m/s2)
20 cm
40 cm
60 cm
80 cm
Tablo 6.2 Büyük top için T,g-Sarkaç uzunluğu tablosu
10- Şimdi de küçük top için aynı işlemleri gerçekleştiriniz.
Uzunluk
1. Ölçüm
2. Ölçüm
3. Ölçüm
Ortalama
T(80 cm)
T(60 cm)
T(40 cm)
T(20cm)
Tablo 6.3 Küçük top için periyot-sarkaç uzunluğu tablosu
Her bir periyot için yer çekimi ivmesini (g) hesaplayınız. Sonuçları tabloya yerleştiriniz.
g(20)=…………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
g(40)=…………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
g(60)=…………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
g(80)=…………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Küçük Top
T(s)
g(m/s2)
20 cm
40 cm
60 cm
80 cm
Tablo 6.4 Küçük top için T,g-Sarkaç uzunluğu tablosu
11- Her iki kütle için T2(s2) - l(m) grafiğini çiziniz ve bağıl hatayı hesaplayınız.
12- Büyük ve küçük top için aynı uzunluktaki sarkaçların periyodunda bir fark söz konusu
mudur? Her bir uzunluk için Periyot-Kütle grafiğini çiziniz.
23
Deney No
Deneyin Adı
Deneyin Amacı
: M7
: HOOKE KANUNU
Teorik Bilgi
:
:Ucuna kütle asılan yayın, harmonik hareketini gözleyerek periyodunun
hesaplanması ve yayın kuvvet sabitinin bulunması.
Yay, F kuvvetinin etkisiyle x kadar uzamış bulunsun, bu halde kuvvetle uzama miktarı
arasındaki ilişki
7.1
F  kx
ile verilir. Burada k yayın kuvvet (esneklik) sabitidir. Yaylar için bu ifade Hooke Kanunu
olarak bilinir. Yay ucuna asılan kütle yayı geren kuvvettir. Bir yayın ucuna farklı ağırlıkta
cisimler bağlanarak gerginliğinin ölçülmesi yayın esnekliğinin test edilmesini sağlar. k’nın
değeri yayın sertliğinin bir ölçüsüdür. Sert yayların k değeri büyük, yumuşaklarınki küçüktür.
Doğrusal bir eksen üzerinde, yerdeğiştirmeyle orantılı esnek bir geri çağırıcı kuvvetin
etkisi altında sabit bir nokta etrafında eşit zaman aralıklarında gidip gelen ve hiçbir sürtünme
kuvvetinin etkisinde bulunmayan cismin hareketine Harmonik Hareket denir. Yay ucuna
asılan kütle x konumunda dengede iken çok az aşağı çekilip bırakılırsa x noktası etrafında
kütlenin harmonik hareket yaptığı gözlenir. m kütlesinin herhangi bir noktadan aynı yön ve
doğrultuda iki kez geçmesi için geçen zamana harmonik hareketin Titreşim Periyodu denir.
Titreşim periyodu T, yayın kuvvet sabitine ve yaya bağlı olan m kütlesine bağlıdır. Aşağıdaki
gibi ifade edilir;
m
7.2
T  2
k
Eğer yayın kütlesi cismin kütlesine göre çok küçük değilse, sistemin eşdeğer kütlesini elde
etmek için yayın kütlesinin salınan cismin kütlesine eklenmesi gerekir. Aksi durumda yayın
kütlesi ihmal edilebilir.
Deneyin Yapılışı:
1. Şekil 7.1 deki gibi deney düzeneğini kurun.
2. Herbir yayın uzunluğunu ölçün.
Lkalın = ........... , Lince = ............
3. Üç tane farklı kütle için (m1= 10g, m2= 20g ve m3= 40g) yayların uzama miktarını bulun.
L1 = ......... , L2 = ......... , L3 = ......... (Kalın yay için)
l1 = ......... , l2 = ......... , l3 = ……… (İnce yay için)
4. Eşitlik (1)’i kullanarak her bir kütle için yayların esneklik sabitini (kkalın, kince) hesaplayın,
kalın ve ince yay için bulduğunuz değerlerin ortalamasını alın ve yaylar için (F, L) grafiğini
milimetrik grafik kâğıdına çizin, eğimden yayın esneklik sabitini bulun (k1, k2).
kkalın1 = ........... , kkalın2 = ........... , kkalın3 = ...........; kk.ortalama = .........
kince1 = …….… , kince2 = …..…… , kince3= …………;
k1 = ..........., k2 = ...........
24
ki.ortalama = ...........
Şekil 7.1: a) Deney Düzeneği
b) Düzenek veri okuma biçimi
5. Yine bu üç kütle için denge konumundan düşey olarak çok az çekerek salınıma bırakın ve
her bir kütle için 10 salınım periyodu süresince geçen zamanı kronometre ile ölçerek
kaydediniz. 10’a bölerek bir tek salınım için geçen zamanı yani periyodu (T) bulunuz. (T2, m)
grafiğini çizerek eğimi hesaplayınız. (eğim = T2/ m )
6. Eşitlik 7.2’den yayın esneklik katsayısını çekersek (k = 42 / eğim) elde edilir. Bu formülü
ve 5.adımdaki sonuçları kullanarak esneklik katsayısını hesaplayın ve 4. adımdaki sonuçlarla
karşılaştırın.
kk = ......... , ki = .........
7.
Herbir kütle için bulduğunuz uzama boyunu (L, l) ve yayların esneklik sabitlerini
kullanarak eşitlik 7.4’den işi hesaplayın.
Bulduğunuz değerleri tablolara yerleştirin.
Kütle (kg)
0
M1
M2
M3
Kuvvet (N)
L (m)
L (m)
kince (N/m)
kkalın(N/m)
Kütle (kg)
m1
m2
T (s)
m3
Deney Raporu
:
1)
Grafikler milimetrik grafik kâğıdına çizilerek teslim edilecek.
2)
Tablodaki boşluklar ve herbir adımda istenen değerler yazılarak karşılaştırmalar
yapılacak.
3)
Aşağıdaki formül dikkate alınarak yayın kuvvet sabiti ve periyot için hata hesabı
yapılacak.
 Tdeney  T formül

T
% ET  %

 100 %

T formül 
T formül


 k grafik  k formül

k
%Ek  %

 100 %

k formül 
k formül


Sorular
:
1. Bu deneyde yay yerine katı çubuk kullanılsaydı çubuk ta Hooke kanununa uyar mıydı?
2. Bir yayın periyodunu kutuplarda ve ekvatora yakın bir noktada ölçtüğümüzde farklılık
görür müyüz? Bunu nasıl açıklarsınız?
3. Periyodu (T) ve yerçekimi ivmesini (g) birbirine bağlayan ifadeyi türetiniz.
26
Deney No
Deneyin Adı
Deneyin Amacı
: M8
: ISI KAPASİTESİ
: Düşük sıcaklıkta su ile doldurulmuş kalorimetre kabı içine ısıtılmış
metal nesneler daldırılarak suyun sıcaklığındaki artıştan, metallerin ısı kapasitelerinin
belirlenmesi.
Teorik Bilgi
:
Herhangi bir maddenin birim kütlesinin sıcaklığını bir derece değiştirmek için cisme
verilmesi veya ondan alınması gereken ısı miktarına bu cismin özısı kapasitesi denir ve c ile
gösterilir. Cismin bir m kütlesine bir Q ısı miktarı aktığında, bu kütlenin sıcaklığı T kadar
Q
artacaktır. Bu sebepten ifadeyi yeniden düzenlediğimizde özısı kapasitesi c 
olur.
mT
J
Tanımdan özısı kapasitesinin birimi
olarak bulunur. Isı içeren birçok deney
kg 0C
kalorimetre denilen kapalı bir kapta yapılır. Kalorimetri denilen kap ısıyı dışarı kaçırmayacak
veya çevresinden ona ısı girişi olmayacak şekilde tasarlanmıştır. Değişik sıcaklıklardaki iki
veya daha çok malzemenin birlikte bir kalorimetrenin içine yerleştirildiğini düşünelim. Bu
malzemeler ısıl enerjilerini, hepsi aynı sıcaklığa ulaşana kadar, yani ısıl denge kurulana kadar
bölüşeceklerdir. Kalorimetre içinde alınan ve verilen ısıların toplamı sıfır olacatır. Bir başka
deyişle, bir kalorimetre kabında  1 sıcaklığında ms gram su varken,  2 sıcaklığında, özgül
ısısı C olan mc gramlık bir cisim konursa ısı alışverişi sonunda bütün cisimler aynı  3
sıcaklığına ulaşır. Dışarıdan alınan toplam ısı 0 olduğundan
msu csu  3  1   mc C  3   2   0
eşitliği yazılabilir.
Deneyin Yapılışı :
Deneyde kullanılacak malzemeler Şekil 8.1 de gösterilmiştir.
1- Deney yapacağınız metal blokları teker teker tartınız (mc).
2- Kalorimetre kabına, oda sıcaklığında kütlesi bilinen (msu) kadar su koyunuz.
3- Sıcaklığını okuyunuz (1).
4- Isı kapasiteleri ölçülecek olan metalleri cam kaba koyunuz (Şekil 8.1). Cam kabı su ile
doldurduktan sonra kaynamaya bırakınız.
Şekil 8.1
27
5- Cam kaptan alınan 2 sıcaklığındaki cisim su dolu kalorimetre kabına konur. Başlangıç
anında, 30 sn sonra ve 1, 2, 3, 5, 7 ve 9. dakikalarda kalorimetre kabındaki sıcaklık
değerini gösteren termometreden sıcaklığı okuyunuz. Okunan değerleri verilen tabloya
kaydedip Şekil’8.2 deki gibi bir grafik elde ediniz. Grafikte y-eksenini kesen noktayı
bulunuz. Bu değer karışımın son sıcaklığı olacaktır (3). Mesela aşağıdaki grafikte bu
değer 30°C’dir.
6- Cismin ısınma ısısı değeri (özısı) c’yi msu csu 3  1   cmc 3  2   0 denkleminden
elde ediniz (csu=1 kal/g 0C olarak alınacaktır).
Su
27
o
Sıcaklık ( C)
30
24
21
18
0
2
4
6
8
10
Zaman (dk)
Şekil 8.2
Sonuçlar
:
Tablo 8.1
Pirinç
mpirinç=……….. (g)
Zaman
Sıcaklık
(dak.)
(0C)
0
½
1
2
3
5
7
9
28
Demir
mdemir=……….. (g)
Zaman
Sıcaklık
(dak.)
(0C)
0
½
1
2
3
5
7
9
Alüminyum
mAl=……….(g)
Zaman
Sıcaklık
(dak.)
(0C)
0
½
1
2
3
5
7
9
Tablo 8.2- Hesaplamalar
Pirinç için;
1 ( 0C )
2 ( 0C )
3 ( 0C )
msu (g)
c(kal/g 0C)
1 ( 0C )
2 ( 0C )
3 ( 0C )
msu (g)
c(kal/g 0C)
Aliminyum için;
1 ( 0C )
2 ( 0C )
3 ( 0C )
msu (g)
c(kal/g 0C)
Demir için;
Deney raporu yazarken analiz esnasında;
1. Al, Fe ve pirinç için özısı (c) değerlerini bulunuz.
2. Bulduğunuz değerleri oda sıcaklığı için kabul edilmiş değerleri ile (kitaplardan veya
internetten bulunuz) kıyaslayınız.Her üç malzeme için hata hesabı yapınız.
DeneyselDeğer  TeorikDeğer
(Formül: Hata% 
100 )
TeorikDeğer
3. Her üç malzeme için (Zaman Sıcaklık) grafik çiziniz.
4. Deneyde öğrendiklerinize dair yorumunuzu; “hesaplar, hatalar, grafikler ve neler
öğrendiğimiz hakkında” yazınız. Hiçbir deney (olumlu ya da olumsuz) asla sonuçsuz
bırakılmamalıdır. Hata sebepleri, gözlenenlerin ve diğer sonuçların yorumu muhakkak
yapılmalıdır.
Sorular
:
1. Isı ile sıcaklık arasındaki farkı açıklayın. CGS sistemindeki birimlerini yazınız.
2. Termodinamiğin temel yasaları nelerdir? Açıklayınız.
29