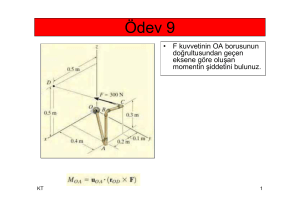
VEKTÖRLER
KT
YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
1
Mekanik olayları ölçmekte ya da değerlendirmekte
kullanılan matematiksel büyüklükler:
• Skaler büyüklük: sadece bir sayısal değeri
tanımlamakta kullanılır, pozitif veya negatif
olabilir. Kütle, hacim ve uzunluk statikte sıkça
kullanılan skalerlerdir.
• Vektörel büyüklük: Şiddet, doğrultu ve yön ile
belirtilen fiziksel bir büyüklüktür. Kuvvet,
moment, konum vektörel birer büyüklüktür.
Vektör, yönlenmiş bir doğru parçasıyla temsil
edilir.
KT
2
• Vektörün, doğrultusunu bir doğru, yönünü bir ok,
şiddetini de okun boyu belirler.
A
• Vektörler harfin üzerine kısa bir ok çizilerek gösterilir.
• Bu şekilde gösterilen vektörün şiddeti “A” ile ifade edilir.
KT
3
Vektörel İşlemler
• Vektörün bir skalerle çarpımı veya bölümü
• bir vektörün bir skalerle çarpımı veya bölümü, yine aynı
vektör doğrultusunda yeni bir vektör verir. Bu vektörün
şiddeti, skaler ile mevcut vektörün şiddetinin çarpımına
eşittir
KT
4
Vektörlerin Toplamı
• Vektörler paralelkenar ilkesi kullanılarak birbiriyle
toplanır. A ve B vektörleri başlangıç noktalarında
birleştirilir. Her bir vektörün ucundan diğer vektöre çizilen
paralel doğrular paralelkenarı oluşturur. R bileşkesi A ve
B’nin başlangıcından doğruların kesiştiği noktaya çizilen
doğrudur. R bileşkesi paralelkenarın köşegenidir.
R A B
KT
5
Vektörlerin Toplamı
• A ve B vektörlerini paralelkenar ilkesinin özel bir
uygulaması olan “üçgen ilkesi”ne göre de toplayabiliriz.
• A vektörünün ucuna B vektörü eklenir, A’nın başlangıcı
ile B’nin ucu birleştirilir ve R bileşke vektör elde edilir.
Vektör toplamı komutatif’tir,
vektörler herhangi bir
KT
sırada toplanabilir.
R A B B A
6
Vektörlerin Toplamı
• A ve B vektörü aynı etki çizgisine sahipse
paralelkenar kuralı cebirsel (skaler)
toplama indirgenir.
• R= A+B (şiddetlerin toplamı)
KT
7
Vektör Çıkarması
• A ve B vektörlerinin çıkarılması için paralelkenar veya üçgen kuralı
kullanılabilir. A ve B vektörleri arasındaki fark bileşke vektörü:
R A B A ( B)
• Vektör toplamı için uygulanan kurallar vektör çıkarması için de
kullanılmaktadır.
KT
8
Kuvvetlerin Vektörel Toplamı
• Kuvvetler, belli bir büyüklük, doğrultu ve yöne
sahiptir ve vektörel bir büyüklük olduğu için
paralelkenar kuralına göre toplanır.
• Statikteki iki genel problem:
– Bileşenlerden bileşke kuvvet bulmak
– Bilinen bir kuvveti bileşenlerine ayırmak
KT
9
Bir kuvvetin bileşenlerine ayrılması
• Bir noktaya etkiyen bir tek vektör yerine aynı etkiyi
yapacak iki veya daha fazla vektör koymak
mümkündür.Bunlara vektörün bileşenleri denir. Bu
bileşenleri bulabilmek için:
– İki bileşenden düzlemde biri, uzayda ise üç bileşenden ikisi
bilinmelidir.
– Bileşenlerin tesir çizgileri bilinmelidir.
KT
10
İkiden fazla kuvvetin toplanması
• İkiden fazla kuvvet toplanacaksa, bileşke kuvveti bulmak
için paralelkenar kuralı birden fazla uygulanabilir.
KT
FR ( F1 F2 ) F3
11
Analizde izlenecek yol
• Paralelkenar kuralı
• Trigonometri
KT
12
Örnek 1
• F1 ve F2 kuvvetlerinin
bileşkesini ve yönünü
bulunuz.
• Çözüm:
KT
13
Örnek 1
• Kosinüs teoremi’nden:
• Sinüs teoreminden:
KT
14
Örnek 2
• Bu iki kuvvetin bileşkesinin y
ekseni üzerinde olması için F
kuvvetinin şiddetini bulunuz.
200 N
200 N
KT
F
200 N
Sin 60 Sin 45
F 245 N
FR
200 N
Sin 75 Sin 45
FR 273 N
200 N
15
Örnek 3
• 600N’luk kuvveti u ve v
eksenlerinde
bileşenlerine ayırınız.
600 N
KT
16
600 N
Fu
600 N
sin 120 sin 30
Fv
600 N
sin 30 sin 30
Fu 1039 N
Fv 600 N
Örnek 4
F2 kuvvetinin şiddetini, yönünü
ve bileşke kuvveti bulunuz.
(bileşke kuvvet x ekseni
üzerinde, F2 kuvveti ise
minimum şiddette olsun)
Düzlemsel kuvvetlerin toplanması
(Kartezyen Koordinatlar)
• Eğer bir kuvvet x ve y eksenlerindeki bileşenlerine
ayrılırsa, bu bileşenlere “kartezyen bileşenler” denir.
• x ve y eksenleri pozitif ve negatif yönler belirttiklerinden,
bir kuvvetin dik bileşenlerinin büyüklüğü ve yönü cebirsel
skalerlerle ifade edilebilir.
Skaler gösterim:
Fx F . cos
Fy F . sin
KT
19
• F vektörünün yönü, açısı yerine küçük eğim üçgeni ile de
gösterilebilir.
a
Fx F ( ) veya
c
b
Fy F ( ) veya
c
Fx a
F c
Fy b
F c
• Fy vektörünün yönü negatif y ekseninde olduğundan y
bileşeni negatiftir, bu nedenle hesaplamalarda (-) işareti
kullanılmalıdır.
KT
20
Kartezyen vektör gösterimi
• Bir kuvvetin bileşenleri,
kartezyen birim vektörler
cinsinden ifade edilebilir.
x ve y eksenlerinin
doğrultularını belirtmek
için sırasıyla i ve j
kartezyen birim vektörleri
kullanılır. Bu vektörler,
boyutsuz birim
uzunluktadır ve yönleri
(ok ucu), pozitif veya
negatif x ve y eksenini
işaret etmesine bağlı
olarak, artı veya eksi
işareti ile gösterilir.
KT
F Fx iˆ Fy ˆj
21
Aynı düzlemdeki kuvvetlerin bileşkeleri
• Bir kuvvetin bileşenlerini göstermede kullanılan iki
yöntem de çok sayıda düzlemsel kuvvetin bileşkesini
belirlemek için de kullanılabilir. Bunun için, her bir kuvvet
önce x ve y bileşenlerine ayrılır ve sonra karşılıklı
bileşenler aynı doğru üzerinde bulunduklarından skaler
cebir kullanılarak toplanır.
F1 F1x iˆ F1 y ˆj
F2 F2 x iˆ F2 y ˆj
F3 F3 x iˆ F3 y ˆj
KT
22
Aynı düzlemdeki kuvvetlerin bileşkeleri
FR F1 F2 F3
VEKTÖREL TOPLAM
FR F1x iˆ F1 y ˆj F2 xiˆ F2 y ˆj F3 x iˆ F3 y ˆj
( F1x F2 x F3 x )iˆ ( F1 y F2 y F3 y ) ˆj
FRx iˆ FRy ˆj
SKALER TOPLAM
FRx F1x F2 x F3 x
FRy F1 y F2 y F3 y
KT
23
İkiden fazla kuvvetin toplanması
FRx Fx
FRy Fy
KT
• Herhangi bir sayıda düzlemsel kuvvetin
bileşkesinin x ve y bileşenleri, bütün
kuvvetlerin x ve y bileşenlerinin cebirsel
toplamıyla bulunabilir.
24
FRx Fx
FRy Fy
• Bileşkenin bileşenleri belirlendikten sonra, şekildeki gibi,
x ve y eksenleri boyunca çizilebilir. Bileşke kuvvet vektör
toplamından belirlenebilir. Bileşkenin büyüklüğü ve yönü
ise şu şekilde bulunabilir.
FR F
tan
KT
1
2
Rx
F
2
Ry
FRy
FRx
25
Örnek 5:
• Şekilde gösterilen
kuvvetlerin bileşkesini
birim vektörleri
kullanarak bulunuz
KT
26
F1x 200. sin 30 100 N
F1 y 200. cos 30 173 N
F2 x
12
F2 x 240 N
260 N 13
F2 y
5
F2 y 100 N
260 N 13
F1 100iˆ 173 ˆj N
F2 240iˆ 100 ˆj N
FR F1 F2
140iˆ 73 ˆj N
KT
27
Örnek 6
• Etkiyen kuvvetlerin
bileşkesinin y ekseni
boyunca olması ve
şiddetinin de 800 N
olması için F1 kuvvetinin
şiddetini, açısının ne
olması gerektiğini
bulunuz
KT
28
Örnek 7
• Şekilde gösterilen
kuvvetlerin bileşkesini
bulunuz
ÇÖZÜM 1:
ÇÖZÜM 2:
Kartezyen Vektörler
• Vektör işlemleri, üç boyutlu problemlerin
çözümüne uygulanırken vektörler kartezyen
vektör formunda ifade edilirse işlem basitleşir.
• Sağ El Koordinat Sistemi:
– Vektör cebri işlemlerinde
sağ el koordinat sistemi
kullanılacaktır.
KT
34
Bir vektörün kartezyen bileşenleri
• Bir A vektörünün x, y, z koordinat
eksenlerinde bileşenleri olabilir.
Paralelkenar kuralını iki kez ard
arda uygulayarak;
A A Az
A Ax Ay
A Ax Ay Az
KT
35
Kartezyen birim vektörler
• Üç boyutlu uzayda, i, j, k kartezyen birim
vektörleri sırasıyla x, y, z eksenlerinin
doğrultusunu göstermek için kullanılır. Şekilde
verilen vektörler, pozitif birim vektörlerdir.
KT
36
Kartezyen vektör gösterimi
• Vektörleri kartezyen
bileşenler cinsinden
yazmak önemli bir
avantaj sağlar. Her bir
bileşen vektörün şiddeti
ve yönünü belirtir.
A Axiˆ Ay ˆj Az kˆ
KT
37
Kartezyen vektörün büyüklüğü
• Kartezyen vektör
formunda ifade edilen bir
A vektörünün şiddetini
bulmak için:
A' Ax 2 Ay
A A' Az
2
2
2
A Ax Ay Az
2
KT
2
2
38
Kartezyen vektörün yönleri
• A vektörünün doğrultusu,
A’nın başlangıç noktası ve bu
noktada yer alan pozitif x, y, z
eksenleri arasında ölçülen
(alfa), (beta), (gama)
doğrultu açıları ile tanımlanır.
Bu açılar 0 ile 180
arasındadır.
• , ve ’yı belirlemek için
A’nın x, y, z eksenleri
üzerindeki izdüşümleri
kullanılır.
KT
39
Yön kosinüsleri
Ax
cos
A
KT
cos
Ay
A
Az
cos
A
40
• A vektörünün doğrultu kosinüslerini elde etmenin kolay
bir yolu, A doğrultusunda bir birim vektör oluşturmaktır.
A Ax ˆ Ay ˆ Az ˆ
uA
i
j k
A A
A
A
A
cos x
A
cos
Ay
A
cos
Az
A
A Ax Ay Az
2
2
2
u A cos iˆ cos ˆj cos kˆ
uA’nın büyüklüğü 1 olduğundan;
cos cos cos 1
2
2
2
A Au A
A cos iˆ A cos ˆj A cos kˆ
A iˆ A ˆj A kˆ
x
KT
y
z
** Eğer bir vektörün
şiddeti ve yön
kosinüsleri biliniyorsa,
A vektörü kartezyen
koordinatlarda ifade
edilebilir.
41
Kartezyen vektörlerin toplanması
KT
42
Örnek 8
F kuvvetini kartezyen vektör
olarak ifade ediniz.
cos 2 cos 2 cos 2 1
Fx (+x) yönünde
olduğu için 60°
olmalı
KT
43
Örnek 9
• F kuvvetini
kartezyen vektör
olarak ifade ediniz
ve F kuvvetinin yön
kosinüslerini
bulunuz
KT
44
F F ' Fz
F ' Fx Fy
Pozisyon (Konum) Vektörleri
• Pozisyon vektörü uzaydaki herhangi iki nokta arasında
yönelen bir kartezyen kuvvet vektörünü formüle etmek
açısından önemlidir.
• r pozisyon vektörü, bir noktanın uzaydaki konumunu
diğer bir noktaya göre belirleyen sabit bir vektördür.
r x iˆ y ˆj z kˆ
KT
47
• Daha genel bir halde, pozisyon vektörü uzaydaki
A noktasından B noktasına da yönelebilir.
Vektör toplamı
KT
48
• r konum vektörü, i, j, k bileşenleri, vektörün
başlangıcının koordinatları A (xA, yA, zA), ucuna
karşı gelen koordinatlardan B (xB, yB, zB)
çıkartılarak bulunabilir.
• Ayrıca, bu üç
bileşenin
uç
uca eklenmesi
r’yi verir. A’dan
başlıyarak B’ye
ulaşılıyor.
KT
49
• A ve B noktalarının, oluşturulan koordinat sistemine göre
koordinatları biliniyorsa, A’dan B’ye giden pozisyon
vektörü bulunabilir ve bu yöndeki birim vektör kolaylıkla
elde edilir:
r : A' dan B' ye
r
u
; birim vektör
r
Bu birim vektörün bileşenleri ,
ve yönlerini vermektedir.
u A cos iˆ cos ˆj cos kˆ
KT
50
Bir doğru boyunca yönelen kuvvet vektörü
• Üç boyutlu statik
problemlerinde, bir
kuvvetin doğrultusu
genellikle etki
çizgisinin geçtiği iki
nokta ile belirlenir.
Şekildeki F kuvveti
buna bir örnektir.
Doğrultusu A’dan B’ye
olan F kuvveti
kartezyen vektör
şeklinde ifade
edilebilir.
KT
51
Bir doğru boyunca yönelen veya iki nokta arasında uzanan
kuvvet vektörü
ANALİZDE İZLENECEK YOL
F, A noktasından B noktasına uzanan bir
doğru boyunca etkiyorsa aşağıdaki şekilde
kartezyen vektör formunda ifade edilebilir:
Konum Vektörü: A’dan B’ye yönelen
konum r vektörü belirlenir ve r büyüklüğü
hesaplanır.
Birim Vektör: Hem r hem de F’nin
doğrultusu ve yönünü tanımlayan u=r/r
birim vektörü belirlenir.
Kuvvet Vektörü: F büyüklüğü ve u
doğrultusu birleştirilerek yani F=Fu ile F
belirlenir.
KT
52
Örnek 10
• Şekilde gösterilen
çatı, AB ve AC
zincirleriyle
taşınmaktadır. A
noktasına etki eden
bileşke kuvveti
kartezyen vektör
olarak ifade edin.
KT
53
A (0,0,4)
B (4,0,0)
C (4,2,0)
KT
54
Örnek 11
• A noktasına etki eden
kuvveti kartezyen
vektör olarak ifade
edin.
KT
55
Nokta (Skaler) Çarpım
• Statikte bazen iki doğru arasındaki açının, veya bir
kuvvetin bir doğruya paralel ve dik bileşenlerinin
bulunması gerekir. İki boyutlu problemlerde trigonometri
ile çözülebilir, ancak 3 boyutluda çözüm için vektör
yöntemleri uygulanmalıdır.
• Skaler çarpım, iki vektörün çarpımı için özel bir
yöntemdir.
• A ve B vektörlerinin skaler çarpımı, AB şeklinde yazılır
ve A skaler çarpım B diye okunur. A ve B’nin
büyüklükleri ile iki vektör arasındaki açının kosinüsünün
çarpımı olarak tanımlanır.
A B A B cos
0 180
o
o
57
• Bu çarpıma skaler çarpım veya nokta çarpım da
denir. Bu işlemin kuralları :
– Değişme özelliği (komütatiflik )
– Skaler ile çarpım
– Dağılma kuralı (distributiflik)
A B B A
a( A B) (aA) B A (aB)
A ( B D) ( A B) ( A D)
58
Kartezyen vektör formülasyonu
Formülünü kullanarak kartezyen
vektörlerin çarpımını bulmak
A B A B cos birim
için kullanılabilir.
Örneğin: iˆ iˆ (1)(1) cos 0o 1
ˆj ˆj 1
kˆ kˆ 1
iˆ ˆj (1)(1) cos 90o 0
iˆ kˆ 0
kˆ ˆj 0
59
Uygulamalar1
• Skaler çarpımın mekanikte iki önemli uygulama
alanı vardır:
– 1) İki vektör veya kesişen doğrular arasındaki açı
A B A B cos
60
Uygulamalar 2
• 2) Bir vektörün bir doğruya paralel ve dik bileşenlerinin
bulunması:
Aa: a-a doğrultusundaki A vektörünün bileşeni. A’nın izdüşümü de denir.
a-a’nın doğrultusu ua birim vektörüyle belirlenmişse, Aa vektörünün şiddeti
skaler çarpımla bulunabilir.
Aa A ua
(ua 1)
Au a cos A cos
Aa A ua şeklinde bulunur .
61
• A vektörünün dik bileşeni:
A A Aa A A Aa A ( A cos )ua
1 A u a
A A sin veya
cos
A
A A2 Aa ' den bulunur .
2
62
ÖRNEK 12
Şekilde verilen
F kuvvetinin
AB çubuğuna
paralel ve dik
bileşenlerini
bulunuz.
A (0; 0; 0)
B (2; 6; 3)
rB 2iˆ 6 ˆj 3kˆ
63
iˆ iˆ (1)(1) cos 0o 1
ˆj ˆj 1
kˆ kˆ 1
iˆ ˆj (1)(1) cos 90o 0
iˆ kˆ 0
kˆ ˆj 0
64