deney

BÖLÜM 5
TRANSİSTÖRLÜ YÜKSELTEÇ
Amaç: Ortak emetörlü yükselteç devresinin incelenmesi, bias gereksiniminin irdelenmesi,
yükselteç kazancı ile giriş direncinin ölçülmesi
BİLGİ
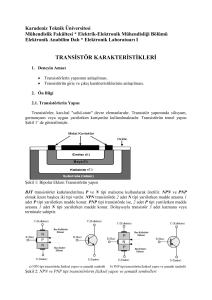
5.1 Transistörlü Yükselteç: Şekil 5.1’de
verilen ortak emetörlü devre ile VBE giriş
geriliminin değişimi arttırılabilir ve çıkışta
daha büyük VCE gerilim değişimi elde
edilebilir. Böyle bir devre yükselteç
(“amplifikatör”) olarak anılır. Bu devrede
VBE ’nin (dolayısıyla I B ’nin) belirli bir
değeri için akacak olan I C kolektör
akımının RC direnci üzerinde oluşturduğu
RC I C gerilim düşmesi ile transistörün
uçları arasındaki VCE geriliminin toplamı
VCC kaynak gerilimine eşit olacağından,
VCC  RC I C  VCE
(5.1)
ifadesi yazılabilir. Bu bağıntı ise bir
doğruyu belirler ve yük doğrusu olarak
anılır (Şekil 5.2). O halde kolektör akımı,
yük doğrusu ile, devreye uygulanan I B
akımına karşıt gelen çıkış öz eğrisinin
(Bölüm 4, paragraf 4.5) Q kesim noktası
tarafından belirlenir. Devrede VBE ’nin
değişimi (5.1) bağıntısında,
I C ’nin
değişmesine; o da RC direnci üzerindeki
gerilim düşmesi nedeni ile VCE ’nin
değişmesine yol açar. Ancak VBE ’nin
belirli bir V eşik geriliminin altında
olması halinde baz akımı akmadığından
I C  0 , dolayısıyla VCE  VCC olacağına
dikkat edilmelidir.
Ayrıca VBE ’nin belirli bir değeri aşması durumunda transistör doyma (satürasyon) bölgesine
gireceğinden, I C ’nin artık artmayacağı, dolayısıyla VCE ’nin sabit kalacağı da
unutulmamalıdır. VBE ’nin bu iki değer arasında kalması halinde VCE sürekli kontrol
edilebilecek ve değişimi de yaklaşık lineer olacaktır. Silisyum bir transistörün gerilim geçiş
eğrisi yaklaşık Şekil 5.3’deki gibidir: bu şekilden de kolayca anlaşılacağı üzere VBE  V için
VCE  VCC ; ancak VBE  VBE,sat için ise VCE  VCE ,sat ’dir. Öte yandan Şekil 5.3’ten
anlaşılacağı üzere VBE ’nin değişimi
VCE değişimine göre küçük olduğundan
Şekil 5.1’deki devre ile VBE gerilim
farkının yükseltilebileceği, dolayısıyla bu
devrenin yükselteç işlevini sağladığı
kolayca anlaşılabilir. Bir yükselticinin, Av
gerilim kazancı en genel halde Vout çıkış
geriliminin Vin giriş gerilimine oranı
olarak tanımlandığından
Av 
Vout
Vin
(5.2)
dir. O halde değişken bir giriş işareti için
Vin  VBE ve Vout  VCE olduğundan,
kazanç
Av 
VCE
VBE
(5.3)
bağıntısı ile verilir. Ancak pratikte transistör akımlarının kabul edilen yönleri dolayısıyla
(Bölüm4, paragraf 4.2) Av ’nin işaretinin negatif olacağı kolayca anlaşılabilir.
5.2Transistörün Öngerilimlenmesi: Şekil
5.1’de verilen yükselteç devresinin girişine
VBE gerilimi yerine vbe değişken gerilimi,
örneğin alternatif gerilim uygulanırsa,
Şekil 5.3’den de anlaşılacağı üzere, vbe ani
V  vbe  VBE,sat
geriliminin
olması
halinde vCE çıkış geriliminin ani değerinin
bir anlamı olacaktır; vbe ’nin bu sınırların
dışında olması durumunda ise vCE , VCC
veya VCE , sat gibi sabit değerlere eşit olur.
Dolayısıyla vbe  0 sükunet durumunda, başka bir deyişle giriş işareti olmadığı zaman
transistörden belirli bir I EQ akımının akmasını, yani bir VCEQ geriliminin oluşmasını
sağlamak gerekir: bu ise transistörün belirli bir çalışma noktasında öngerilimlenmesi veya
kutuplanması (“biaslama”) demektir. Bunun için V g  vbe değişken gerilimine VBB doğru
gerilimi eklenebilir. Ancak bunun bazı mahsurları vardır: VBB ve VCC gibi iki gerilim
kaynağına ihtiyaç olduğu gibi, baz akımının doğru bileşeni de değişken gerilim kaynağından
akar. Halbuki transistörün belirli bir çalışma noktasında kutuplanması tek bir gerilim kaynağı
kullanarak Şekil 5.4’deki basit bir devre ile sağlanabilir.
5.3 Transistörün AC Eşdeğer Devreleri:Bir yükselteç devresinde kullanılan transistörün
davranışının daha iyi incelenebilmesi için eşdeğer devreden yararlanılır. En çok h (hibrit)
parametreleri ve r parametreleri ile belirlenen eşdeğer devreler kullanılır. Bu devrelerde
kolaylıkla ölçülebilen, ayrıca transistörle ilgili bilgi verilerinde de yer alan ve Tablo 5.1’de
özetlenen dört temel h parametresinden faydalanılır.
Tablo 5.1
Tanımı
h parametresi
Koşulu
hi
Giriş direnci
Çıkış kısa devre
hr
Geri besleme oranı
Giriş açık devre
hf
İleri yönde akım kazancı
Çıkış kısa devre
Çıkış direncinin tersi(  çıkış kondüktansı)
ho
Giriş açık devre
Bu dört parametrenin her biri ikinci bir alt indisle devrenin türüne bağlı olarak ifade edilir:
örneğin “ hie ” ortak emetörlü devrenin giriş direncini, “ hob ” ortak bazlı devrenin çıkış
kondüktansını...v.s belirler.
h parametreleri ile ortak emetörlü devrenin
AC eşdeğer devresi Şekil 5.5’deki gibidir.
Bu
devredeki
h
parametrelerinin
büyüklükleri
hie  Vb / I b
hre  Vb / Vc
(5.4)
h fe  I c / I b
hoe  I c / Vc
dir. Eşdeğer devrelerde h parametrelerine göre belki daha kolaylık sağlayan r parametreleri
de çok kullanılır. Bu r parametreleri ve bunların h parametrelerine eşitlikleri Tablo 5.2’de
verilmiştir.
Tablo 5.2
 ac
Tanımı
AC alfa ( I c / I e )
 ac
AC beta ( I c / I b )
h fe
re
rb
AC emetör direnci
AC baz direnci
hre / hoe
hie  hre / hoe  1  h fe 
rc
AC kolektör direnci
r parametreleri
h parametreleri
h fb
hre  1 / hoe
r
parametreleri
ile
transistörün
basitleştirilmiş AC eşdeğer devresi Şekil
5.6’daki gibidir. Burada belirtilen  ac ,
(4.2) bağıntısı ile verilen ve  dc olarak
tanımlanabilecek akım kazancından farklı
olarak
 ac 
I c
I b
(5.5)
olarak ifade edilir. Ayrıca oda sıcaklığında,
re emetör direncinin, yaklaşık olarak
re 
25mV 
IE
(5.6)
bağıntısı ile ifade edilebileceği de
gösterilebilir. Diğer taraftan RC kolektör
direnci ve R E emetör dirençleriyle oluşan
bir yükselteç devresinin r parametreleriyle
eşdeğer devresi Şekil 5.7’deki gibi
olacaktır. Bu devrenin bazdan görülen Rin
iç direnci
Rin 
Vb
Ib
(5.7)
dir. Ayrıca
Vb  I e re  RE 
(5.8)
ve (5.5)’den
Ib 
Ic
 ac
olduğundan, I c  I e ise
Rin   ac re  RE 
(5.9)
bağıntısı elde edilir. ancak RE  0 ise, (5.6)’dan
Rin 
Ic
I
re   e 25  25 veya
Ib
Ib Ic Ib
Rin K  
25
I b A
(5.10)
dir. Öte yandan Şekil 5.8’de verilen bir
yükselticinin AC gerilim kazancı (5.2)
bağıntısına göre
Av 
Vc
Vb
dir. Ancak bu şekilden
Vc   ac I c RC  I e RC
ve ayrıca (5.8) bağıntısından
Av 
I e RC
RC

I e re  RE  re  RE 
(5.11)
dir. Ancak RE  0 ise, (5.6)’dan
Av 
dir.
RC
R I
 C e veya
re
25mV 
Av  40 RC I c  40Vc
(5.12)
DENEY
A)Gerilim Kazancının Belirlenmesi:
1)Digiac
3000
Semiconductors-1
modülünün 7 nolu düzeni yardımıyla Şekil
5.9’daki devre gerçekleştirilir. 0-12V
gerilim kaynağı ile devreye osiloskopla
ölçülerek 9V uygulanır.
2)0-2V gerilim kaynağı ayarlanarak,
osiloskopla
ölçülen
kolektör
VC
geriliminin 4V olması sağlanır.
3) VBE baz-emetör gerilimi
ölçülerek Tablo 5.3’e geçirilir.
DM
ile
4)Benzer şekilde VC 6V’a ayarlanır VBE gerilimi ölçülür, Tablo 5.3’e işlenir.
5) VCE ve VBE değerlerinden değişimleri hesaplanır. Yükselticinin Av gerilim kazancı (5.3)
bağıntısıyla belirlenerek sonuçlar Tablo 5.3’e işlenir.
Tablo 5.3
VC V 
VBE V 
VCE
VBE
Av
B)Öngerilimleme Gereksiniminin İncelenmesi:
1)
Digiac
3000
Semiconductors-1
modülünün
8
nolu
düzeninden
yararlanılarak Şekil 5.10’daki devre
gerçekleştirilir. SG’nin çıkış
genliği
minimum
seviyedeyken, 0-12V gerilim
kaynağı ile devreye 8V uygulanır.
2)SG ile devreye uygulanacak
sinüs
geriliminin frekansı 1kHz’e ayarlanır ve
çıkış genliği minimum seviyede tutulur.
3) SG’nin genliği yavaş yavaş arttırılarak
çıkış gerilimi gözlenir. Başlarda çıkış geriliminde bir değişme görülmemesine karşılık, genlik yaklaşık 0,6V’a eşit olduğunda
dar bir negatif darbe (puls) izlenir ve bu durum kayda alınır.
çıkışta
4)Aynı devrede bazı değişiklikler yapılarak Şekil 5.11’deki biaslı devre gerçekleştirilir.
Devrenin V BEQ ve VCEQ sükunet gerilimleri ölçülerek, Tablo 5.4’e geçirilir.
5)Deneyin başında ayarlanan 8V ile
ölçülen VCEQ değerinden 3,9K’lık R18
kolektör direnci üzerindeki VR18 gerilim
düşmesi hesaplanır. Bu devrenin Av (hesap)
kat kazancının (“stage gain”) yaklaşık
değeri (5.12) bağıntısıyla belirlenir, sonuç
Tablo 5.4’e işlenir.
6)Osiloskopla gözlenen bias ve çıkış
gerilimleri çizilir.
7)Giriş geriliminin uygulanabilmesi için,
SG’nin
çıkış
genliği
minimum
seviyedeyken devre Şekil 5.12’dekine
dönüştürülür. Devreye yine 8V uygulanır.
SG’nin çıkış
(kolektör) genliği
değiştirilerek, çıkışında p-p V  3V elde
edilmesi sağlanır. Osiloskopla gözlenen
giriş ve çıkış gerilimleri yukarıda çizilen
grafik üzerine geçirilir. Elde edilen
Av (ölçü) kazancı belirlenerek Tablo 5.4’e
yazılır.
Tablo 5.4
VBEQ V 
VCEQ V 
VRC V 
Av (hesap)
Av (ölçü)
C)Giriş Empedansının Ölçülmesi:
1)Transistörün giriş empedansının etkisinin incelenmesi için Şekil 5.12’deki devreden
yararlanılır. Osiloskopla 0-12V gerilim kaynağı 8V’a ve SG’nin çıkış genliği minimum
seviyede iken frekansı yine 1kHz’e ayarlanır. SG’nin çıkış genliği arttırılarak devre çıkışında
p-p V  3V elde edilmesi sağlanır.
2)Osiloskopla gözlenen bias ve çıkış gerilimleri çizilir, çıkıştaki işaretin bozulması
(distorsiyon) dikkatlice incelenir.
3)Devrede bazı değişiklikler yapılarak
Şekil 5.13’deki devre gerçekleştirilir ve
27K’lık R15 direnci girişe seri bağlanır.
SG’nin çıkış genliği arttırılarak çıkışta yine
p-p V  3V elde edilir.
4)Osiloskopla gözlenen çıkış gerilimi
çizilerek yukarıda gözlenenle karşılaştırılır.
5)Devrede yapılan bazı değişikliklerle
Şekil 5.14’deki devre gerçekleştirilir; DC
ampermetre olarak kullanılan DM ile
sükunet durumundaki I BQ baz akımı
ölçülür, Tablo 5.5’e işlenir.
Tablo 5.5
I BQ A
Rin k 
6)Bu değerden transistörün Rin giriş
empedansının yaklaşık değeri (5.10)
bağıntısıyla hesaplanır, sonuç Tablo 5.5’e
geçirilir.
7)Şekil
5.13’deki
devre
tekrar
gerçekleştirilerek,
Şekil
5.15’de
gösterildiği gibi AC voltmetre olarak
kullanılan DM ile R15 direnci üzerindeki
VR15 gerilim düşmesi, Vin giriş gerilimi ve
Vout çıkış gerilimleri ölçülür, sonuçlar
Tablo 5.6’ya geçirilir.
8)27K’lık direnç ile Rin empedansı seri bağlı olduklarından Vin / Rin = VR15 /27K bağıntısından
Rin hesaplanır, Tablo 5.6’ya işlenir. Bulunan bu sonuç yukarıda bulunan yaklaşık değerle
karşılaştırılır.
9) Vout ve Vin değerlerinden Av hesaplanır, sonuç Tablo 5.6’ya işlenir. Bu değer yukarıda
Av
hesaplanan
(hesap)
yaklaşık
kat
kazancı
ile
karşılaştırılır.
Tablo 5.6
VR15  mV 
Vin mV 
Vout V 
Rin k 
Av
SORULAR
1)Bir yükseltecin girişine p-p değeri 40mV olan bir işaret uygulandığında kolektör geriliminde
2,4 ila 7,2V’luk bir değişim oluşuyorsa kat kazancı nedir?
2)Ortak emetörlü bir yükseltecin girişine p-p değeri yeterince büyük bir sinüs gerilimi
uygulanırsa çıkış gerilimi nasıldır?
3)Biaslı bir yükselteç devresinde besleme gerilimi VCC  5,8V , baz direnci Rb  1M ve bazemetör gerilim farkı Vbe  0, 6V ise, devrenin yaklaşık giriş empedansı ne kadardır?
4)Bu yükselteçte kolektör direnci RC  2, 2 K ve kolektör-emetör gerilim farkı Vce  2,94V
ise, yaklaşık kat kazancı nedir?