Slide 1 - Ninova

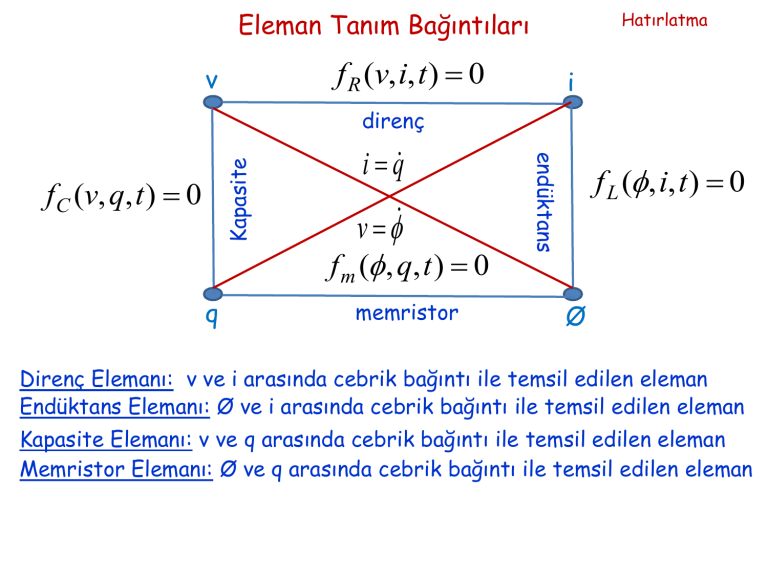
Eleman Tanım Bağıntıları
Hatırlatma
f R (v, i, t )  0
v
i
fC (v, q, t )  0
q
i  q
v  
f m ( , q, t )  0
memristor
endüktans
Kapasite
direnç
f L ( , i, t )  0
Ø
Direnç Elemanı: v ve i arasında cebrik bağıntı ile temsil edilen eleman
Endüktans Elemanı: Ø ve i arasında cebrik bağıntı ile temsil edilen eleman
Kapasite Elemanı: v ve q arasında cebrik bağıntı ile temsil edilen eleman
Memristor Elemanı: Ø ve q arasında cebrik bağıntı ile temsil edilen eleman
2-Uçlu Direnç Elemanları
• lineer, lineer olmayan, zamanla değişen, değişmeyen, akım
ve/veya gerilim kontrollü dirençlerin tanım bağıntıları,
• seri, parallel bağlı dirençlere ilişkin uç bağıntıları,
• lineer olmayan dirençlere ilişkin dc (doğru akım) çalışma
noktasının belirlenmesi, küçük işaret analizi.
Lineer Direnç
+
()
v(t )  Ri (t )
direnç
i (t )  Gv(t )
iletkenlik, siemens
mho
v
v (t )
(S )
i (t )
v (t )
i (t )
i-v düzlemi
v-i düzlemi
Hatırlatma: Lineerlik
f ( x1 )  y1
f ( x2 )  y2
f (.) lineer
f (x1  x2 )  f ( x1 )  f ( x2 )
 y1  y 2
Özel Lineer Dirençler:
Açık devre elemanı
f (i, v)  i  0
v (t )
i (t )
R
G0
i (t )
i-v düzlemi
v (t )
v-i düzlemi
Kısa devre elemanı
f (i, v)  v  0
v (t )
i (t )
R  0 i (t )
i-v düzlemi
G
v (t )
v-i düzlemi
Açık devre elemanı ve kısa devre elemanının i-v,v-i karakteristiklerine
dikkat edelim !!!
v (t )
i (t )
R
G0
i (t )
i-v düzlemi
v (t )
v-i düzlemi
Tanım: (Dual Dirençler)
A direncinin v-i karakteristiği B direncinin i-v karakteristiği ile aynıdır.
A direnci B direncinin dual’idir.
Lineer direnç elemanına ilişkin ani güç
Lineer Olmayan Direnç
+
v
_
f ( v, i )  0
p(t )  v(t )i (t )  Ri 2 (t )
Bazı Özel Lineer Olmayan Dirençler
İdeal Diyot
+
v
_
RID  {( v, i) : vi  0, i  0, v  0 ve v  0, i  0}
Diyot tıkamada
Diyot iletimde
(v  0),
(i  0),
i0
v0
v (t )
i (t )
i (t )
v (t )
i(t )
i-v düzlemi
v-i düzlemi
Diyot tıkamada iken davranışı hangi eleman gibi?
Is
v(t )
Diyot iletimde iken davranışı hangi eleman gibi?
p-n Jonksiyon Diyodu (alçak frekanslardaki özellikleri)
+
v
_
uç büyüklükleri
v
RD  {( v, i ) : i  I s [exp( )  1], I s , vT sabit }
vT
q elektron yükü
kT
I s ters doyma akımı VT 
k Boltzman sabiti
q
T Sıcaklık (Kelvin)
VT  0,026V
Tünel Diyod
+
RTD  {( v, i ) : i  iˆ(v)}
v
i (t )
İ1
v1  v  v2 eğim negatif
_
osilatör, kuvvetlendirici
İ2
İ 2  i  İ1 her akıma
üç gerilim karşılık düşüyor
hafıza, anahtarlama
V1 V2
gerilim kontrollü, akım kontrollü değil
Bağımsız kaynaklar
Bağımsız gerilim kaynağı
+
+
vs (t ) vs (t )
_
_
v(t )
Rvs  {( v, i) : v  vs (t ),  i  }
i (t )
v (t )
Bağımsız gerilim kaynağı lineer eleman mı?
Bağımsız gerilim kaynağı gerilim kontrollü mü?
Bağımsız gerilim kaynağı akım kontrollü mü?
vs (t )  3V
Bağımsız akım kaynağı
+
is (t )
v
Ris  {( v, i) : i  is (t ),  v  }
_
Zamanla Değişen Dirençler
v-i karakteristiği zamanla değişen dirence zamanla değişen direnç denir.
Lineer Zamanla Değişen Direnç
+
v
v(t )  R(t )i (t )
v (t )
R (t )
i (t )  G (t )v(t )
i (t )
_
t
Anahtar
i
+
v
_
S(t)
t
S(t)
v
i
+
+
v
_
Seri ve Paralel 2-uçlu Direnç Elemanlarının
Oluşturduğu 1-Kapılılar
i
N
1-kapılısı
i kapı akımı
v kapı gerilimi
1-kapılının özellikleri
kapı akımı ve gerilimi
cinsinden yazılır
Seri bağlı 2-uçlu dirençler
i d1
i1
+
+
R1
v1
v
d2
R2
N
_
d3
_
i
+2
v2
_
+
N
1-kapılısı
v
_
Tanım Bağıntıları
v1  vˆ1 (i1 )
KAY
v2  vˆ2 (i2 )
KGY
i  i1
1. düğüm
1-2-3-1 düğüm dizisi
i1  i2
2. düğüm
v1  v2  v  0
v1  v2  v
Amaç:
v  vˆ(i ) bağıntısını bulmak
KGYv
+
KAYv
 v1  v2
 vˆ1 (i )  vˆ2 (i ) ˆ vˆ(i )
i
+
R1
i1
+
v1
_
_
v
R2
N
Sonuç:
_
v  vˆ1 (i)  vˆ2 (i)
v2
+
i2
KAY
tüm elemanların akımı kapı akımı ile aynı
KGY
kapı gerilimi eleman gerilimlerinin toplamı
elemanlar akım kontrollü elde edilen 1-kapılı da akım kontrollü
Bir soru: İki uçlunun tanım bağıntısını elde ediniz
Bir başka soru:
Bu iki uçlunun da tanım bağıntısını elde ediniz
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits”, Mc.Graw Hill, 1987, New York
Paralel bağlı 2-uçlu dirençler
Tanım Bağıntıları
i d1
+
+
v v1
N
_
_
i1
+
R1 v2
_
i1  iˆ1 (v1 )
i2
KGY
2 düğümü referans alınırsa
KAY
1. düğüm
R2
d2
Amaç: i
KAY
+
ETB
+
KGY
i2  iˆ2 (v2 )
i  i1  i2
i  iˆ1 (v1 )  iˆ2 (v2 )
i  iˆ1 (v)  iˆ2 (v) ˆ iˆ(v)
v  v1  v2
i  i1  i2
 iˆ(v )
bağıntısını bulmak
Bir soru: İki uçlunun tanım bağıntısını elde ediniz
Bir başka soru:
Bu iki uçlunun da tanım bağıntısını elde ediniz
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits”, Mc.Graw Hill, 1987, New York
İki uçluların tanım bağıntısını elde ediniz
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits”, Mc.Graw Hill, 1987, New York