FİZİKSEL KİMYA
3- KATILAR
3- KATILAR
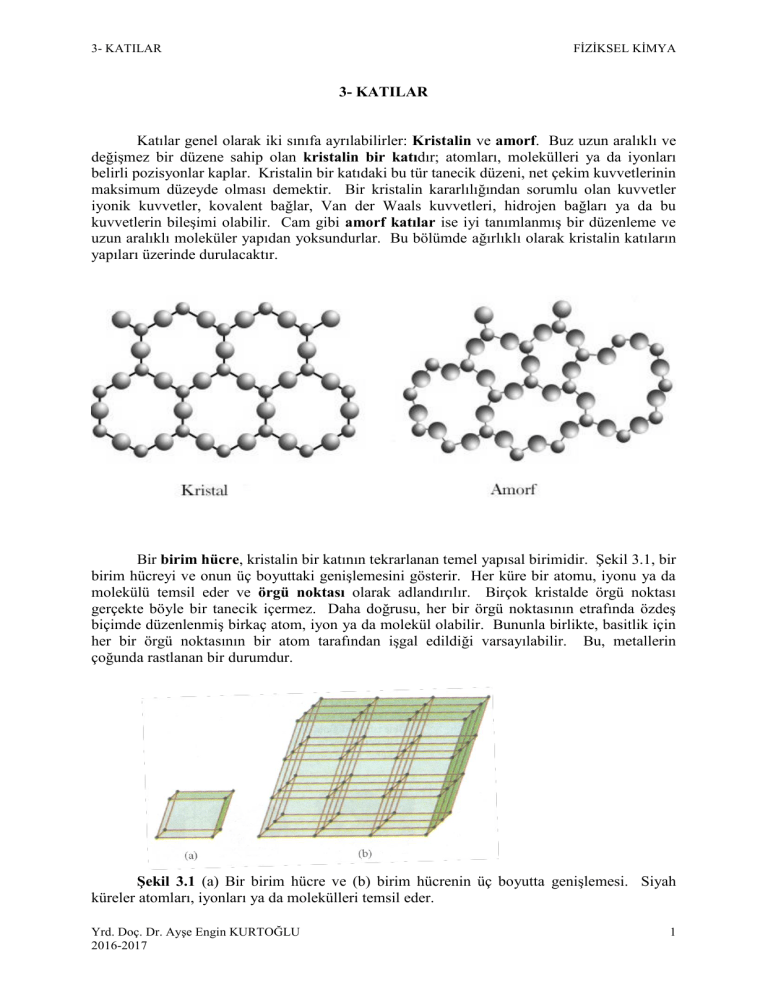
Katılar genel olarak iki sınıfa ayrılabilirler: Kristalin ve amorf. Buz uzun aralıklı ve
değişmez bir düzene sahip olan kristalin bir katıdır; atomları, molekülleri ya da iyonları
belirli pozisyonlar kaplar. Kristalin bir katıdaki bu tür tanecik düzeni, net çekim kuvvetlerinin
maksimum düzeyde olması demektir. Bir kristalin kararlılığından sorumlu olan kuvvetler
iyonik kuvvetler, kovalent bağlar, Van der Waals kuvvetleri, hidrojen bağları ya da bu
kuvvetlerin bileşimi olabilir. Cam gibi amorf katılar ise iyi tanımlanmış bir düzenleme ve
uzun aralıklı moleküler yapıdan yoksundurlar. Bu bölümde ağırlıklı olarak kristalin katıların
yapıları üzerinde durulacaktır.
Bir birim hücre, kristalin bir katının tekrarlanan temel yapısal birimidir. Şekil 3.1, bir
birim hücreyi ve onun üç boyuttaki genişlemesini gösterir. Her küre bir atomu, iyonu ya da
molekülü temsil eder ve örgü noktası olarak adlandırılır. Birçok kristalde örgü noktası
gerçekte böyle bir tanecik içermez. Daha doğrusu, her bir örgü noktasının etrafında özdeş
biçimde düzenlenmiş birkaç atom, iyon ya da molekül olabilir. Bununla birlikte, basitlik için
her bir örgü noktasının bir atom tarafından işgal edildiği varsayılabilir. Bu, metallerin
çoğunda rastlanan bir durumdur.
Şekil 3.1 (a) Bir birim hücre ve (b) birim hücrenin üç boyutta genişlemesi. Siyah
küreler atomları, iyonları ya da molekülleri temsil eder.
Yrd. Doç. Dr. Ayşe Engin KURTOĞLU
2016-2017
1
3- KATILAR
FİZİKSEL KİMYA
Her kristalin katı aşağıdaki şekilde görülen yedi tip birim hücreden biri olarak tanımlanabilir.
Tüm kenarları ve tüm açıları eşit olduğundan, kübik birim hücrenin geometrisi özellikle
basittir. Birim hücrelerin herhangi biri üç boyutlu uzayda tekrarlandığında kristalin bir
katının tipik örgü yapısı oluşur.
Şekil 3.2 Yedi çeşit birim hücre vardır. açısı b ve c kenarları ile, β açısı a ve c
kenarları ile ve açısı a ve b kenarları ile belirlenir.
Kürelerin İstiflenmesi
Birkaç eşdeğer kürenin üç boyutlu düzenli bir yapı oluşturmak için farklı şekillerde
istiflenmesi göz önünde bulundurularak, kristal oluşumu için genel geometrik koşullar
anlaşılabilir. Kürelerin katmanlar halinde düzenlenme şekli, ne tip birim hücreye sahip
olunduğunu belirler.
Kürelerin oluşturduğu bir katman, en basit durumda Şekil 3.3 (a)’ da görüldüğü gibi
düzenlenebilir.
Şekil 3.3 Basit kübik hücredeki eşdeğer kürelerin düzenlenmesi. (a) Bir katmanın
üstten görünüşü. (b) Basit kübik hücrenin tanımı. (c) Her küre sekiz birim hücre tarafından
paylaşıldığından ve bir küpte sekiz köşe olduğundan, basit bir kübik birim hücrede bir tam
kürenin eşdeğeri bulunur.
Yrd. Doç. Dr. Ayşe Engin KURTOĞLU
2016-2017
2
3- KATILAR
FİZİKSEL KİMYA
Koordinasyon sayısı, bir kristal örgüdeki bir atomun (ya da iyonun) etrafındaki
atomların (ya da iyonların) sayısı olarak tanımlanır. Onun değeri bize kürelerin ne kadar sıkı
istiflendiğinin ölçüsünü verir ve daha büyük koordinasyon sayısı birbirine daha yakın küreler
demektir.
Diğer kübik hücre tipleri gövde merkezli kübik hücre (gmk) ve yüzey merkezli kübik
hücredir (ymk) (Şekil 3.4). İkinci katmandaki kürelerin ilk katmanın çukurlarına ve üçüncü
katmanın, ikinci katmanın çukurlarına yerleştiği gövde merkezli kübik düzen basit bir küpten
farklıdır (Şekil 3.5). Bu yapıdaki her kürenin koordinasyon sayısı 8’ dir (Her küre üst
katmandaki dört küre ve alt katmandaki dört küre ile temastadır). Yüzey merkezli kübik
hücrede, sekiz köşedeki kürelere ek olarak küpün altı yüzünün her birinin merkezinde de
küreler vardır.
Şekil 3.4 Üç tip kübik hücre. Gerçekte atomları, iyonları ya da molekülleri temsil
eden küreler bu kübik hücrelerde birbirleriyle temas halindedirler.
Şekil 3.5 Bir gövde merkezli kübikteki eşdeğer kürelerin düzeni. (a) Üstten görünüş.
(b) Gövde merkezli kübik birim hücrenin tanımı. (c) Gövde merkezli kübik birim hücrede iki
tam kürenin eşdeğeri bulunur.
Kristalin bir katıdaki her birim hücre, diğer birim hücrelere bitişik olduğundan, bir
hücrenin atomlarının çoğu komşu hücrelerle paylaşılır. Örneğin tüm kübik hücre tiplerindeki
her köşe atomu sekiz birim hücreye aittir (Şekil 3.6 a). Yüzey merkezli bir atom iki birim
hücre tarafından paylaşılır (Şekil 3.6 b).
Yrd. Doç. Dr. Ayşe Engin KURTOĞLU
2016-2017
3
3- KATILAR
FİZİKSEL KİMYA
Şekil 3.6 (a) Herhangi bir hücredeki köşe atomu sekiz birim hücre tarafından
paylaşılır. (b) Bir kübik hücredeki yüzey merkezli atom iki birim hücre tarafından paylaşılır.
Basit kübik ve gövde merkezli kübik hücrelerde yüzey merkezli kübik hücredekinden
daha fazla boşluk vardır. Kürelerin en etkili düzenlenmesi, en sıkı istiflenme, A katmanı
olarak adlandırılan, Şekil 3.7’ de görülen yapı ile başlar.
Şekil 3.7 (a) Sıkı istiflenmiş bir katmandaki her küre, diğer altı küre ile temas
halindedir. (b) İkinci katmandaki küreler, ilk katmandaki küreler arasındaki çukurlara
yerleşirler. (c) Sıkı istiflenmiş hekzagonal yapıdaki üçüncü katman kürelerinin her biri birinci
katman kürelerinin üzerine yerleşirler. (d) Sıkı istiflenmiş kübik yapıdaki üçüncü katman
kürelerinin her biri, birinci katmandaki çukurların üzerine karşılık gelen çukurlara yerleşirler.
Yrd. Doç. Dr. Ayşe Engin KURTOĞLU
2016-2017
4
3- KATILAR
FİZİKSEL KİMYA
Kristallerden X Işını Kırınımı
Kristal yapı hakkında tüm bilinenler, X ışını kırınım çalışmalarından öğrenilir. X ışını
kırınımı, X ışınlarının kristalin bir katı biriminden saçılması ile ilgilidir. Katı şebekedeki
taneciklerin düzenini anlamak için saçılma ya da kırılma ile oluşturulmuş modeller kullanılır.
Alman fizikçi Max ve Laue, X ışınlarının dalga uzunluğu kristaldeki örgü noktaları
arasındaki uzaklıklarla kıyaslanabilecek büyüklükte olduğundan, şebekenin X ışınlarını
kırabildiğini gösterdi. Bir X ışını kırınım modeli, X ışınlarına dalgaların eşlik etmesinin
sonucudur.
Şekil 3.8, tipik bir X ışını kırınım düzeneğini gösterir. Bir X ışınları demeti bir yüzeye
sabitlenmiş kristale yönlendirilir. Kristaldeki atomlar gelen radyasyonun bir kısmını
absorplar ve daha sonra yeniden yayınlar, bu işlem X ışınlarının saçılması olarak adlandırılır.
Şekil 3.8 Bir kristalin X ışını kırınımını elde etmek için oluşturulmuş düzenek.
Kalkan, kırılmamış X ışınlarının fotoğraf plağına zarar vermesini önler.
Bir kırınım modelinin nasıl oluşturulabildiğini anlamak için, X ışınlarının iki paralel
düzlemdeki atomlar tarafından saçılmasını düşünelim (Şekil 3.9). Başlangıçta, iki gelen ışık
birbiri ile aynı fazdadır (maksimumları ve minimumları aynı pozisyonlarda bulunur). Daha
aşağıdaki dalga ikinci katmandaki bir atom tarafından saçılırken daha yukarıdaki dalga birinci
katmandaki bir atom tarafından saçılır ya da yansıtılır. Saçılmış iki dalganın yeniden aynı
fazda olabilmesi için, daha aşağıdaki dalga tarafından kat edilmiş ek uzaklık, X ışınının dalga
boyunun () tam katı olmalıdır. Yani,
BC+CD = 2.d.Sin = n.
n=1, 2, 3, …
(3.1)
: X ışınları ile kristal düzlem arasındaki açı
d: Bitişik düzlemler arasındaki uzaklık
Yrd. Doç. Dr. Ayşe Engin KURTOĞLU
2016-2017
5
3- KATILAR
FİZİKSEL KİMYA
Şekil 3.9 X ışınlarının iki atom katmanından yansıtılması. Aşağıdaki dalga
yukarıdakinden 2.d.Sin kadar daha uzun bir yol kat eder. İki dalganın kırılma sonrasında
yeniden aynı fazda olması için 2.d.Sin=n. olmalıdır. (n=1, 2, 3, …) ise , X ışınının dalga
boyudur. Şekildeki noktalar yalnız kristal yüzlerce paralel katman içerirse gözlenir.
X ışını kırınım tekniği, katı haldeki moleküllerdeki bağ uzunluklarını ve bağ açılarını
bulmak için en duyarlı yöntemi sunar. Elektron yoğunluğu düzey haritası, bir molekülün
çeşitli yerlerindeki bağıl elektron yoğunlukları ile ilgili bilgi verir.
Örnek 3.1 0,154 nm dalga boylu X ışınları bir kristalden 14,17o’ lik bir açı yaparak
kırılırlar. n=1 olduğunu varsayarak, kristaldeki katmanlar arası uzaklığı (pm) cinsinden
hesaplayınız.
Yanıt:
1 nm=1000 pm
n.=2.d.Sin
(3.1) eşitliğinden,
1000 pm
1.0,154 nm.
1 nm
n.
d
348,8 pm
2.Sin
2.Sin14,17
Amorf Katılar
Kristal yapıdaki katılar son derece kararlıdırlar. Ancak, bir katı hızla oluşturulursa
(örneğin, bir sıvı hızla soğutulursa) atomları ve molekülleri sıralanacak zamanı bulamazlar ve
düzenli bir kristalinkinden farklı pozisyonlarda bulunabilirler. Oluşan katıya amorf adı
verilir. Amorf katılar belli bir sıcaklık aralığında gitgide yumuşarlar ve akıcılık kazanırlar.
Yumuşamanın başladığı bu noktaya camsı geçiş sıcaklığı denir. Cam gibi amorf katıların
atomları üç boyutlu düzenden yoksundurlar. Cam genellikle, kristallenmeksizin katı halde
soğutulmuş olan, inorganik malzemelerin optikçe saydam bir eritme ürününü temsil eder.
Eritme ürünüyle, cam sodyum oksit (Na2O), bor oksit (B2O3) ve renk ve diğer özellikler için,
bazı geçiş metal oksitleri gibi bileşikler ile temel bileşeni olan eritilmiş silisyum dioksitin
karıştırılması ile oluşur. Bazı konularda cam bir katıdan çok bir sıvı gibi davranır. X ışını
kırınım araştırmaları camda uzun aralıklı periyodik düzenin bulunmadığını gösterir.
Bugün genel kullanımda bulunan, yaklaşık 800 farklı cam çeşidi vardır. Tablo 3.2
kuvars, pyreks ve soda kireç camının bileşimini ve özelliklerini gösterir.
Yrd. Doç. Dr. Ayşe Engin KURTOĞLU
2016-2017
6
FİZİKSEL KİMYA
3- KATILAR
Tablo 3.2 Üç Çeşit Camın Bileşimi ve Özellikleri.
ADI
BİLEŞİMİ
Saf kuvars camı
% 100 SiO2
Pyrex cam
SiO2, % 60-80
B2O3, % 10-25
Al2O3, az miktarda
Soda-kireç camı
SiO2, % 75
Na2O, % 15
CaO, % 10
ÖZELLİKLERİ
VE
KULLANIM ALANLARI
Düşük termal genleşme,
geniş
bir
dalga
boyu
aralığında saydam.
Optik
araştırmada kullanılır.
Düşük termal genleşme,
görünür
ve
kızılötesine
saydam,
ancak
UV
radyasyona
değil.
Laboratuvarda ve mutfaktaki
ateşe dayanıklı cam eşya
yapımında kullanılır.
Kimyasal
maddeler
tarafından kolayca tahrip
edilen ve termal değişimlere
duyarlı.
Görünür ışığı
geçirir,
ancak
UV
radyasyonu absorbe eder.
Başlıca pencere camlarının
ve
şişelerin
yapımında
kullanılır.
Camın rengi, büyük ölçüde metal iyonlarının (oksitleri halinde) varlığından
kaynaklanır. Örneğin, yeşil cam, demir (III) oksit (Fe2O3) ya da bakır (II) oksit (CuO) içerir,
sarı cam, uranyum (IV) oksit (UO2) içerir, mavi cam, kobalt (II) oksit (CoO) ve bakır (II)
oksit (CuO) içerir ve kırmızı cam, küçük altın ve bakır parçacıkları içerir. Burada bahsedilen
metal iyonlarının çoğu geçiş metalleridir.
Katıların Atomik Isıları
Özgül (spesifik) ısının, bir maddenin 1 gramının sıcaklığını 1 oC arttırmak için gerekli
olan ısı miktarı olduğunu “Sıvılar” konusunu işlerken tanımlamıştık. Basit katı bir maddede
bulunabilen en küçük parçalar, gazlardaki moleküller yerine genel olarak atomlar olarak
düşünüldüğünden burada atomik ısılar göz önüne alınır. Sabit hacim ve basınçtaki atomik
ısılar arasındaki fark, birkaç onda bir kadardır. Bütün katı elementlerin atomik ısıları, yani
atom kütleleriyle özgül (spesifik) ısıları çarpımı cal cinsinden yaklaşık olarak 6,3’ e eşittir.
Dulong-Petit Yasası denilen bu yasa atom kütleleri 30’ dan yüksek olan çoğu elementler
halinde doğrudur. Atom kütleleri küçük ve güç eriyebilen elementler için (C, Si, B gibi)
yasanın doğru olmadığı görülür. Ancak sıcaklık arttırıldığında atomik ısılar normal değere
yaklaşır (Şekil 3.13). Örneğin C (elmas) için atomik ısı 11 oC’ de 1,36 iken 606 oC’ de 5,26’
dır. Ayrıca hiçbir sıcaklıkta katı elementlerin atomik ısıları birbirine eşit değildir, sıcaklık
arttığında özgül (spesifik) ısılar da artar, örneğin tungsten için 1300 oC’ de 8,2’ dir. Mutlak
sıfırda bütün basit katı maddelerin özgül (spesifik) ısıları sıfır olur. Bu durum kuantum
kuramıyla açıklanabilir.
Yrd. Doç. Dr. Ayşe Engin KURTOĞLU
2016-2017
7
FİZİKSEL KİMYA
3- KATILAR
Katılardaki atomlar titreşim hareketlerinde bulunurlar. O halde, katılardaki atomik ısı
yalnız titreşim enerjisinden ileri gelir. Her yönde titreşebilen atomda üç serbestlik derecesi
olduğuna göre, atomik ısı Cv=3.R=5,95 olur. Bu ise 6,3’ e yakındır. Aradaki fark 6,3’ ün Cp’
ye ait olmasındandır.
Tablo 3.3 Oda Sıcaklığında Cp (Katılar İçin).
ELEMENT
Hidrojen
Lityum
Bor
Elmas
Grafit
Oksijen
Flor
Sodyum
Magnezyum
Alüminyum
Silisyum
Cp
2,5
5,5
2,7
1,5
2,0
4,0
5,0
6,8
6,0
5,8
4,9
ELEMENT
Fosfor
Kükürt
Klor
Potasyum
Kalsiyum
Demir
Nikel
Gümüş
Kadmiyum
Altın
Kurşun
Cp
5,5
5,5
6,2
6,9
6,2
5,9
6,2
6,0
6,7
6,1
6,1
Şekil 3.13 Katı elementlerin atomik ısıları.
Örnek 3.2 Kalsiyum (Ca) ve oksijenin (O) atomik ısıları 6,2 ve 4,0 cal.g-1.oC-1 olarak
ölçüldüğüne göre, kalsiyum oksidin (CaO) özgül (spesifik) ısısını hesaplayınız. (Ca: 40
g.mol-1, O: 16 g.mol-1)
Yanıt:
CaO için,
Atomik ısı = 1.6,2+1.4,0 = 10,2
cal.mol-1.oC-1
Dulong-Petit Yasası’ na göre,
Atomik ısı
10,2
10,2
c
0,182 cal.g 1 .o C 1
Atom / Molekül kütlesi 40 16
56
Yrd. Doç. Dr. Ayşe Engin KURTOĞLU
2016-2017
8
FİZİKSEL KİMYA
3- KATILAR
Örnek 3.3 Atom kütlesi 40 olan kalsiyumun (Ca) özgül (spesifik) ısısını hesaplayınız.
Yanıt:
Dulong-Petit Yasası’ na göre,
Atomik ısı
6,2
c
0,155 cal.g 1 .o C 1
Atom / Molekül kütlesi 40
Örnek 3.4 Oda sıcaklığında demirin (Fe) özgül (spesifik) ısısı 0,107 cal.g-1.oC-1 olarak
ölçülmüştür. Demirin atom kütlesini hesaplayınız. Gerçek atom kütlesi 55,8 olduğuna göre
yapılan hata ne kadardır?
Yanıt:
Dulong-Petit Yasası’ na göre,
Atomik ısı
5,9
c
0,107
M 55,14 g.mol1
Atom / Molekül kütlesi
M
% Hata
55,8 55,14
.100 % 1,2
55,8
Katı Bileşiklerin Molar Isıları
Katı bir bileşiğin molar ısısı, yani 1 molgramının sıcaklığını 1 oC arttırmak için
gerekli olan ısı miktarı, molekülü oluşturan atomların atomik ısılarının toplamına eşittir.
Neumann-Kopp Yasası denilen yasa yardımıyla katı bileşiklerin yaklaşık molar ısıları
hesaplanabilir. Bunun için Tablo 3.3’ teki değerlerden yararlanılır.
CaCl2 durumunda atom sayısı 3’ tür, o halde molar ısısı= 3.6,2=18,6 cal.mol-1.oC’ dir.
Oysa deneysel değer 19,3 cal.mol-1.oC (80,75 J.mol-1.oC)’ dir. CaCO3 durumunda ise ayrı ayrı
atomların ısılarını toplamak gerekir:
1.6,2 + 1.2,0 + 3.4,0 = 20,2 cal.mol-1.oC = 84,52 J.mol-1.oC
bulunur.
Sıvılarda özgül (spesifik) ısılar daha büyüktür. Aşağıdaki değerlerden yararlanarak
sıvıların molar ısıları hesaplanabilir:
Tablo 3.4 Oda Sıcaklığında Cp (Sıvılar İçin).
Element
Hidojen
Bor
Karbon
Cp
5,0
4,8
3,0
Element
Oksijen
Flor
Diğer elementler
Cp
6,0
7,0
8,0
Örneğin sülfat asidinin H2SO4’ in molar ısısı için,
2.5,0 + 1.8,0 + 4.6,0 = 42 cal.mol-1.oC =175,73 J.mol-1.oC
bulunur.
Katıların Özgül (Spesifik) Isılarının Sıcaklıkla Değişmesi
Katı maddelerin özgül (spesifik) ısıları mutlak sıfır yakınlarında sıfırdır. Klasik
kuramın açıklayamadığı bu sorunun ilk açıklaması Einstein (1907) tarafından yapılmıştır.
Einstein, bir kristaldeki bütün atomların bir ortalama denge durumlarına göre harmonik
titreşim hareketleri yapan osilatörler (elektriksel salınımları üreten devre) olarak
düşünülebileceğini varsaymıştır. Einstein, her maddenin sabit ve ayırt edici bir titreşim
Yrd. Doç. Dr. Ayşe Engin KURTOĞLU
2016-2017
9
FİZİKSEL KİMYA
3- KATILAR
frekansının () bulunduğunu ve osilatörler tarafından absorplanan enerjinin sürekli olmayıp
Planck Kuramı’ na göre süreksiz bir biçimde olduğunu düşünmüştür. Planck Kuramı’ na göre
osilatörün ortalama enerjisi,
h.
(3.2)
E h . / k .T
e
1
eşitliği ile verilmiştir. Katıda her osilatör atomu üç serbestlik derecesine sahip olduğundan, 1
atomgram gazın enerjisi yukarıdaki eşitliğin 3.N ile çarpılmasıyla elde edilir. , atomun üç
serbestlik derecesine sahip olduğu ayırt edici sıcaklıksa, R.=N.h. alınarak enerji için,
3.R.
(3.3)
E /T
e
1
Molar ısı için,
2
e h . / k .T
dE
h.
Cv
3
.
k
.
N
.
.
h . / k .T
1) 2
dT
k.T (e
(3.4)
ya da,
2
/T
.e
T
C v 3.R. / T
(e
1) 2
(3.5)
ya da,
C v 3.R.E.
T
(3.6)
bulunur ki, katıların molar ısıları için Einstein eşitliğidir. E. ’ ye Einstein Fonksiyonu
T
denir. Düşük sıcaklıklarda
büyüktür, paydada e / T yanında 1 ihmal edilebilir. O halde,
T
2
(3.7)
C v 3.R. .e T 0
t 0
T
C v 3.R.1 3.R
(3.8)
T
t Yüksek
olur. Bu sonuçlara göre, mutlak sıfır yakınında katı maddelerin özgül (spesifik) ısıları sıfır
olmakla birlikte, oldukça yüksek sıcaklıklarda ise Cv=3.R=5,96 cal’ ye eşit olur. Einstein
eşitliği elmas halinde gerçekleştirilmiştir. Cv’ nin 331,3 K’ de deneysel sonucu alınıp buradan
frekansı (=2,79.1013 s-1) bulunmuş ve bu değer eşitliğin diğer sıcaklıklarda uygulanması
için kullanılmıştır. Örneğin 331,3 K’ de Cv (Deneysel)=1,838, Cv (Hesaplanan)=1,752,
1258,3 K’ de Cv (Deneysel)=5,507, Cv (Hesaplanan)=5,442’ dir.
Debye Eşitliği
Einstein Eşitliği birçok durumda (örneğin elmas durumunda olduğu gibi) deneysel
ölçülerle uyarlıkta olmakla birlikte, bazı durumlarda (örneğin Cu, KCl gibi) uyarlık tam
değildir. Daha başarılı bir kuram P. Debye tarafından önerilmiştir. Einstein Kuramı’ nda
katıdaki bütün atomların aynı titreşim frekansına sahip oldukları varsayılmıştır. Oysa her
atom, çevresindeki diğer atomların devamlı etkisinde kalır. O halde tek frekans yerine sıfır
frekansla bir m üst sınır frekansı arasında değişen bir frekanslar spektrumu düşünmek
gerekir. Debye (1913) bu düşünceden hareket ederek deneysel olgularla uyarlıkta olan bir
eşitlik vermiştir. , atomun üç serbestlik derecesine sahip olduğu ayırt edici sıcaklık ise,
Yrd. Doç. Dr. Ayşe Engin KURTOĞLU
2016-2017
10
FİZİKSEL KİMYA
3- KATILAR
h. m
k
(3.9)
R
, m de düşünülen katıda
Burada h Planck sabiti, k Boltzmann sabiti k
N
A
maksimum titreşim sayısıdır. Yüksek sıcaklıklarda Cv=3.R, düşük sıcaklıklarda ise,
dır.
3
3
T
T
(3.10)
C v 77,94.3.R. 464,6.
olur ki, mutlak sıfırda Cv gerçekten sıfır olur. Her madde için ayırt edici sıcaklık sabit
olduğundan, düşük sıcaklıklarda katı bir maddenin atomik ısısı mutlak sıcaklığın üçüncü
kuvvetiyle orantılıdır (Şekil 3.14).
Şekil 3.14 Düşük sıcaklıkta Cv’ nin T ile değişimi.
Yrd. Doç. Dr. Ayşe Engin KURTOĞLU
2016-2017
11