3. BÖLÜM ÖRNEK SORULAR 3-19 Isıl iletkenliği k=0.78 W/moC

3. BÖLÜM ÖRNEK SORULAR
3-19 Isıl iletkenliği k=0.78 W/moC, kalınlığı 6 mm olan 1.2 m yüksekliğinde ve 2 m
genişliğinde bir cam göz önüne alınız. Dış ortamdaki sıcaklık -5oC iken oda sıcaklığı 24 oC’de
tutulan bir günde bu cam penceredeki sürekli ısı hızını ve iç yüzey sıcaklığını bulunuz.
Pencerenin iç ve dış yüzeyindeki taşınım ısı transfer katsayılarını h1=10 W/m2.oC ve h2=25
W/m2.oC olarak alınız ve ışınımla ısı transferini ihmal ediniz.
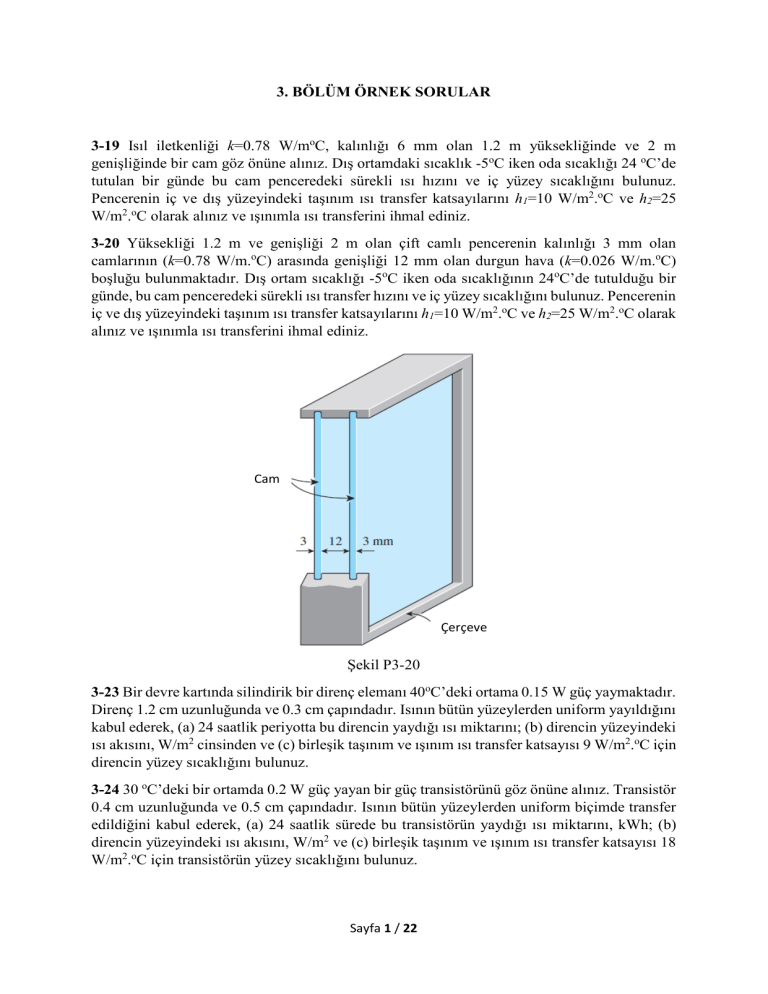
3-20 Yüksekliği 1.2 m ve genişliği 2 m olan çift camlı pencerenin kalınlığı 3 mm olan
camlarının (k=0.78 W/m.oC) arasında genişliği 12 mm olan durgun hava (k=0.026 W/m.oC)
boşluğu bulunmaktadır. Dış ortam sıcaklığı -5oC iken oda sıcaklığının 24oC’de tutulduğu bir
günde, bu cam penceredeki sürekli ısı transfer hızını ve iç yüzey sıcaklığını bulunuz. Pencerenin
iç ve dış yüzeyindeki taşınım ısı transfer katsayılarını h1=10 W/m2.oC ve h2=25 W/m2.oC olarak
alınız ve ışınımla ısı transferini ihmal ediniz.
Cam
Çerçeve
Şekil P3-20
3-23 Bir devre kartında silindirik bir direnç elemanı 40oC’deki ortama 0.15 W güç yaymaktadır.
Direnç 1.2 cm uzunluğunda ve 0.3 cm çapındadır. Isının bütün yüzeylerden uniform yayıldığını
kabul ederek, (a) 24 saatlik periyotta bu direncin yaydığı ısı miktarını; (b) direncin yüzeyindeki
ısı akısını, W/m2 cinsinden ve (c) birleşik taşınım ve ışınım ısı transfer katsayısı 9 W/m2.oC için
direncin yüzey sıcaklığını bulunuz.
3-24 30 oC’deki bir ortamda 0.2 W güç yayan bir güç transistörünü göz önüne alınız. Transistör
0.4 cm uzunluğunda ve 0.5 cm çapındadır. Isının bütün yüzeylerden uniform biçimde transfer
edildiğini kabul ederek, (a) 24 saatlik sürede bu transistörün yaydığı ısı miktarını, kWh; (b)
direncin yüzeyindeki ısı akısını, W/m2 ve (c) birleşik taşınım ve ışınım ısı transfer katsayısı 18
W/m2.oC için transistörün yüzey sıcaklığını bulunuz.
Sayfa 1 / 22
Güç
Transistörü
0.2 W
Şekil P3-24
3-33 Duvarları 4 m yükseklikte ve 12 m uzunlukta olan bir evi göz önüne alınız. Evin iki
duvarında pencere yokken, diğer her iki duvarda 1.0m x 1.5m boyutlarında 6 cm kalınlıklı
camdan (k=0.78 W/m.oC) yapılmış dört adet pencere vardır. Duvarlar 3.3 R değeri (yani L/k
değeri 3.3 m2.oC/W) ile tescil edilmiştir. Pencerelerden doğrudan ışınım kazanımını ve kaybını
ihmal ederek ve evin iç ve dış yüzeylerindeki ısı transfer katsayılarını sırasıyla 11 W/m2.oC ve
22 W/m2.oC alarak pencereli ve penceresiz duvarlardan olan ısı transferlerinin oranını bulunuz.
Tavanarası
4m
12 m
12 m
Camlar
Şekil P3-33
3-52 Yüksekliği 4 m ve genişliği 6 m olan bir duvar, 3 cm’lik olan alçı tabakalarla (k=0.22
W/m.oC) ayrılmış 18cm x 30cm kesitli uzun yatay tuğlalardan (k=0.72 W/m.oC) yapılmıştır.
Ayrıca duvarın her iki yanında 2 cm kalınlığında alçı tabakaları ve ayrıca duvarın iç tarafında
2 cm kalınlığında katı köpük (k=0.026 W/m.oC) bulunmaktadır. İç ve dış sıcaklıklar sırasıyla
22oC ve -4oC; iç ve dış tarafta taşınım ısı transfer katsayıları ise h1= 10 W/m2.oC ve h2=20
W/m2.oC’dir. Isı transferini tek boyutlu alarak ve ışınımı ihmal ederek duvardaki ısı transfer
hızını bulunuz.
Sayfa 2 / 22
Köpük
Harç
Tuğla
Şekil P3-52
3-55 Uzunluğu 12 m ve yüksekliği 5 m olan bir duvar, birbirinden 12cm x 5cm kesitli tahta
dikmelerle (k=0.11 W/m.oC) 16 cm ayrılmış 1 cm kalınlıklı iki alçıpandan (k=0.17 W/m.oC)
yapılmıştır. Direkler düşey olarak 60 cm aralıklı yerleştirilmiş ve aradaki boşluk cam yünü
yalıtımla (k=0.034 W/m.oC) doldurulmuştur. Ev 20oC’de tutulmaktadır ve dış ortam sıcaklığı
-9oC’dir. Evin iç ve dış yüzeylerindeki ısı transfer katsayılarını sırasıyla 8.3 W/m2.oC ve 34
W/m2.oC alarak, (a) örnek bir bölgesini göz önüne alarak duvarın ısıl direncini (b) duvardaki ısı
transfer hızını bulunuz.
3-56 Kalınlığı 25 cm, uzunluğu 9 m ve yüksekliği 3 m olan bir duvar, 18cm x 18 cm kesitli 23
cm’lik dolu tuğladan (k=0.70 W/m.oC) veya aynı boyutta, üzerinde 4cm x 4cm kesitli 23 cm’lik
dokuz tane kare hava deliği (k=0.026 W/m.oC) bulunan delikli tuğladan yapılacaktır. Dört
tarafta bitişik tuğlalar arasında ve duvarın her iki yüzeyinde 1 cm’lik alçı tabakası (k=0.17
W/m.oC) bulunmaktadır. Ev 27 oC’de tutulmaktadır ve dış ortam sıcaklığı 0oC’dir. Evin iç ve
dış yüzeyinde ısı transfer katsayılarını 9 W/m2.oC ve 23 W/m2.oC alarak, (a) dolu tuğlalardan
ve (b) hava delikli tuğlalardan yapılmış duvardan olan ısı transfer hızını bulunuz.
Sayfa 3 / 22
Hava Kanalları
4cm x 4cm x 23cm
1 cm
18 cm
1 cm
Harç
Tuğla
1 cm
23 cm
1 cm
Şekil P3-56
3-57 Örnek kesit alanı şekildeki gibi verilen yüksekliği 5 m, uzunluğu 8 m ve kalınlığı 0.22 m
olan bir duvarı göz önüne alınız. Kullanılan çeşitli malzemelerin ısıl iletkenlikleri kA=kF =2
W/m.oC, kB= 8 W/m.oC, kC=20 W/m.oC, kD=15 W/m.oC ve kE=35 W/m.oC’dir. Duvarın sol ve
sağ yüzeyleri, sırasıyla 300oC ve 100oC uniform sıcaklıklarda tutulmaktadır. Duvardaki ısı
transferinin tek boyutlu olduğunu Kabul ederek, (a) duvardaki ısı transfer hızını; (b) B, D ve E
kısımlarının birleştiği noktanın sıcaklığını ve (c) F kısmındaki sıcaklık düşüşünü bulunuz.
Arayüzeylerdeki temas dirençlerini dikkate almayınız.
Şekil P3-57
Sayfa 4 / 22
3-69 Kalınlığı 1.5 cm olan paslanmaz çelikten (k=15 W/m.oC) yapılmış 8 m iç çaplı küresel bir
tank 0oC’deki buzlu suyun depolanmasında kullanılmaktadır. Tank ortalama sıcaklığı 25oC olan
bir odaya yerleştirilmiştir; odanın duvarlarıda 25 oC’dedir. Tankın dış yüzeyi siyahtır (yayıcılığı
𝜀𝜀=1) ve tankın dış yüzeyi ile çevreleyen yüzeyler arasındaki ısı transferi doğal taşınım ve ışınım
yoluyladır. Tankın iç ve dış yüzeylerindeki taşınım ısı transfer katsayıları sırasıyla 80 W/m2.oC
ve 10 W/m2.oC’dir. (a) Tanktaki buzlu suya olan ısı transfer hızını, (b) 24 saat boyunca 0oC’de
eriyen buzun miktarını bulunuz. Atmosfer basıncında suyun erime ısısı hfg=333.7 kJ/kg’dır.
Toda=25oC
Buzlu Su
Şekil P3-69
3-70 320 oC’deki buhar, iç çapı 5 cm, dış çapı 5.5 cm olan paslanmaz çelik (k=15 W/m2.oC) bir
borudan akmaktadır. Boru kalınlığı 3 cm olan cam yünü yalıtımla (k=0.038 W/m2.oC)
sarılmıştır. Isı 5oC’deki ortama doğal taşınım ve ışınım yoluyla kaybolmaktadır; birleşik doğal
taşınım ve ışınım ısı transfer katsayısı 15 W/m2.oC’dir. Boru içindeki ısı transfer katsayısının
80 W/m2.oC olduğunu kabul ederek boru birim uzunluğu başına buhardan olan ısı kayıp hızını
bulunuz. Ayrıca, boru duvarı ve yalıtımdaki sıcaklık düşüşünü bulunuz.
Sayfa 5 / 22
3. BÖLÜM ÖRNEK SORULARIN CEVAPLARI
3-19
İki yüzeyi verilen belirli sıcaklıklarda tutulan bir cam bulunmaktadır. Camdan olan ısı kaybı
miktarı ve camın iç yüzey sıcaklığı sorulmaktadır.
Kabuller:
Camdan olan ısı transferi süreklidir; çünkü camın iç ve dış yüzey sıcaklıkları verilen değerlerde
sabit kalmaktadır. Isı transferi tek boyutludur; çünkü ısı transferinin gerçekleştiği cam kalınlığı
boyunca önemli bir sıcaklık farkı söz konusudur. Isıl iletkenlik sabittir ve radyasyonla olan ısı
transferi ihmal edilmiştir.
Verilenler:
İç ortam sıcaklığı, 𝑇𝑇∞,1 = 24℃, Dış ortam sıcaklığı, 𝑇𝑇∞,2 = −5℃
Camın ısıl iletkenliği, 𝑘𝑘 = 0.78 𝑊𝑊 ⁄𝑚𝑚 . ℃
İç yüzeydeki ısı taşınım katsayısı, ℎ1 = 10 𝑊𝑊 ⁄𝑚𝑚2 . ℃
Dış yüzeydeki ısı taşınım katsayısı, ℎ2 = 25 𝑊𝑊 ⁄𝑚𝑚2 . ℃
Cam kalınlığı, L=6 mm = 0.006 m, yüksekliği 1.2 m ve genişliği 2 m.
Hesaplamalar:
Cama ait ısıl direnç devresi aşağıda çizilmiştir. Burada ısı transferi iç ortamla camın iç yüzeyi
arasında taşınımla, cam içerisinde iletimle ve camın dış yüzeyiyle dış ortam arasında taşınımla
gerçekleşmektedir. Herbir ısı transfer ortamı için ısıl dirençler;
Cam
Dış Ortam
İç Ortam
𝑇𝑇∞,2 = −5℃
𝑇𝑇∞,1 = 24℃
𝑇𝑇∞,1
𝑅𝑅𝑐𝑐𝑐𝑐𝑐𝑐
𝑇𝑇∞,2
Isı transfer yönüne dik yüzey alanı, 𝐴𝐴 = 𝑦𝑦ü𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘 𝑥𝑥 𝑔𝑔𝑔𝑔𝑔𝑔𝑔𝑔ş𝑙𝑙𝑙𝑙𝑙𝑙 = (1.2)(2) = 2.4 𝑚𝑚2
𝑅𝑅𝑖𝑖 = 𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,1 =
1
1
=
= 0.04167 ℃/𝑊𝑊
ℎ1 𝐴𝐴 (10)(2.4)
Sayfa 6 / 22
𝑅𝑅𝑐𝑐𝑐𝑐𝑐𝑐 =
𝐿𝐿
0.006
=
= 0.00321 ℃/𝑊𝑊
𝑘𝑘𝑘𝑘 (0.78)(2.4)
𝑅𝑅𝑜𝑜 = 𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,2 =
1
1
=
= 0.01667 ℃/𝑊𝑊
ℎ2 𝐴𝐴 (25)(2.4)
Isıl dirençler seri bağlı olduğu için dış ve iç ortam arasındaki toplam ısıl direnç, hesaplanan bu
ısıl dirençlerin toplamına eşittir.
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = 𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,1 + 𝑅𝑅𝑐𝑐𝑐𝑐𝑐𝑐 + 𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,2
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = 0.04167 + 0.00321 + 0.01667 = 0.06155 ℃/𝑊𝑊
Camdan olan ısı transferi hızı;
𝑄𝑄̇ =
𝑇𝑇∞,1 − 𝑇𝑇∞,2 [24 − (−5)]
=
= 471.2 𝑊𝑊
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡
0.06155
Camın iç yüzey sıcaklığı (T1), iç ortam ve camın iç yüzeyi arasında ısı transferi eşitliği yazılarak
bulunabilir;
𝑄𝑄̇ =
𝑇𝑇∞,1 − 𝑇𝑇1
→ 𝑇𝑇1 = 𝑇𝑇∞,1 − 𝑄𝑄̇ 𝑅𝑅𝑡𝑡𝑡𝑡ş,1 = 24 − (471.2)(0.04167) = 4.4℃ elde edilir.
𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,1
3-20
Durgun hava ile ayrılmış çift camlı bir pencereden verilen belirli iç ve dış ortam sıcaklıklarında
gerçekleşen ısı transferinin ve camın iç yüzey sıcaklığının bulunması istenmektedir.
Kabuller:
Camdan olan ısı transferi süreklidir; çünkü camın iç ve dış yüzey sıcaklıkları verilen değerlerde
sabit kalmaktadır. Isı transferi tek boyutludur; çünkü ortamlar arasında ısı transferinin
gerçekleştiği cam kalınlığı boyunca önemli bir sıcaklık farkı söz konusudur. Isıl iletkenlik
sabittir ve radyasyonla olan ısı transferi ihmal edilmiştir.
Verilenler:
İç ortam sıcaklığı, 𝑇𝑇∞,1 = 24℃, Dış ortam sıcaklığı, 𝑇𝑇∞,2 = −5℃
Camın ısıl iletkenliği, 𝑘𝑘𝑐𝑐𝑐𝑐𝑐𝑐 = 0.78 𝑊𝑊 ⁄𝑚𝑚 . ℃
Havanın ısıl iletkenliği 𝑘𝑘ℎ𝑎𝑎𝑎𝑎𝑎𝑎 = 0.026 𝑊𝑊 ⁄𝑚𝑚 . ℃
İç yüzeydeki ısı taşınım katsayısı, ℎ2 = 10 𝑊𝑊 ⁄𝑚𝑚2 . ℃
Dış yüzeydeki ısı taşınım katsayısı, ℎ1 = 25 𝑊𝑊 ⁄𝑚𝑚2 . ℃
Cam kalınlıkları, L1=L3 = 3 mm = 0.003 m, yüksekliği 1.2 m ve genişliği 2 m.
Durgun hava kalınlığı, Lhava =L2=12 mm=0.012 m
Hesaplamalar:
Problemin ısıl direnç devresi aşağıda verilmiştir.
Sayfa 7 / 22
𝑄𝑄̇
Dış Ortam
Durgun
Hava
Cam
𝑇𝑇∞,1 = 24℃
Cam
İç Ortam
𝑇𝑇∞,2 = −5℃
𝑇𝑇∞,1
𝑇𝑇∞,2
Burada Ri iç ortamla sol camın iç yüzeyi arasında olan taşınım ısıl direncidir. R1 ve R3 dirençleri
sırasıyla sol ve sağ taraftaki cam kısımların dirençleri olup değeri birbirine eşittir. Ro direnci
sağ camın dış yüzeyiyle dış ortam arasında olan taşınım ısıl direncidir. Isıl direnç değerleri;
Isı transfer yönüne dik yüzey alanı, 𝐴𝐴 = 𝑦𝑦ü𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘 𝑥𝑥 𝑔𝑔𝑔𝑔𝑔𝑔𝑔𝑔ş𝑙𝑙𝑙𝑙𝑙𝑙 = (1.2)(2) = 2.4 𝑚𝑚2
𝑅𝑅𝑖𝑖 = 𝑅𝑅𝑡𝑡𝑡𝑡ş,1 =
𝑅𝑅1 = 𝑅𝑅3 = 𝑅𝑅𝑐𝑐𝑐𝑐𝑐𝑐 =
1
1
=
= 0.04167 ℃/𝑊𝑊
ℎ1 𝐴𝐴 (10)(2.4)
𝐿𝐿1
𝑘𝑘𝑐𝑐𝑐𝑐𝑐𝑐 𝐴𝐴
𝑅𝑅2 = 𝑅𝑅ℎ𝑎𝑎𝑎𝑎𝑎𝑎 =
𝐿𝐿2
=
𝑘𝑘ℎ𝑎𝑎𝑎𝑎𝑎𝑎 𝐴𝐴
𝑅𝑅𝑜𝑜 = 𝑅𝑅𝑡𝑡𝑡𝑡ş,2 =
𝐿𝐿3
𝑘𝑘𝑐𝑐𝑐𝑐𝑐𝑐 𝐴𝐴
=
=
0.003
= 0.0016 ℃/𝑊𝑊
(0.78)(2.4)
0.012
= 0.1923 ℃/𝑊𝑊
(0.026)(2.4)
1
1
=
= 0.01667℃/𝑊𝑊
ℎ2 𝐴𝐴 (25)(2.4)
Isıl dirençler seri bağlı olduğu için dış ve iç ortam arasındaki toplam ısıl direnç, hesaplanan bu
ısıl dirençlerin toplamına eşittir.
𝑅𝑅𝑡𝑡𝑜𝑜𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 = 𝑅𝑅𝑖𝑖 + 𝑅𝑅1 + 𝑅𝑅2 + 𝑅𝑅3 + 𝑅𝑅𝑜𝑜
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = 0.04167 + 0.0016 + 0.1923 + 0.0016 + 0.01667 = 0.25384℃/𝑊𝑊
Çift camlı pencereden olan ısı transferi hızı;
𝑄𝑄̇ =
𝑇𝑇∞,1 − 𝑇𝑇∞,2 [24 − (−5)]
=
= 114 𝑊𝑊
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡
0.25384
Camın iç yüzey sıcaklığı (T1), iç ortam ve camın iç yüzeyi arasında ısı transferi eşitliği yazılarak
bulunabilir;
𝑄𝑄̇ =
𝑇𝑇∞,1 − 𝑇𝑇1
→ 𝑇𝑇1 = 𝑇𝑇∞,1 − 𝑄𝑄̇ 𝑅𝑅𝑡𝑡𝑡𝑡ş,1 = 24 − (114)(0.04167) = 19.2℃ elde edilir.
𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,1
Sayfa 8 / 22
3-23
Bir devre kartındaki 0.15W gücünde silindirik direnç belirtilen bir ortama sürekli ısı
yaymaktadır. 24 saatte çevreye verilen ısı miktarı, direncin yüzey ısı akısı ve direncin yüzey
sıcaklığının bulunması istenmektedir.
Kabuller:
Sürekli rejim şartları mevcuttur. Isı silindirik direncin bütün yüzeylerinden uniform olarak
transfer edilmektedir.
Verilenler:
Ortam sıcaklığı, 𝑇𝑇∞ = 40℃
Direncin çapı, D=0.3 cm=0.003 m, Direncin uzunluğu, L=1.2 cm =0.012 m
Birleşik taşınım ve ışınım ısı transfer katsayısı, ℎ = 9 𝑊𝑊 ⁄𝑚𝑚2 . ℃
Hesaplamalar:
a) 24 saat boyunca dirençten ortama yayılan ısı transfer miktarı;
𝑄𝑄 = 𝑄𝑄̇ ∆𝑡𝑡 = (0.15)(24) = 3.6 𝑊𝑊h
b) Direncin yüzey ısı akısı;
Silindirik yüzeyin ısı transfer yüzey alanı:
𝜋𝜋𝐷𝐷2
𝜋𝜋(0.003)2
+ 𝜋𝜋𝜋𝜋𝜋𝜋 = 2
+ 𝜋𝜋(0.003)(0.012) = 0.000127 m2
𝐴𝐴𝑠𝑠 = 2
4
4
𝑄𝑄̇
0.15
𝑞𝑞̇ =
=
= 1181 𝑊𝑊/𝑚𝑚2
𝐴𝐴𝑠𝑠 0.000127
Direnç
c) Direncin yüzey sıcaklığı;
Silindirik dirençte üretilen enerji, yüzeylerden ortama taşınımla transfer edilir. Bu
durumda Newton’un soğuma kanunundan;
𝑄𝑄̇
0.15
𝑄𝑄̇ = ℎ𝐴𝐴𝑠𝑠 (𝑇𝑇𝑠𝑠 − 𝑇𝑇∞ ) → 𝑇𝑇𝑠𝑠 = 𝑇𝑇∞ +
= 40 +
= 171.2℃ bulunur.
(9)(0.000127)
ℎ𝐴𝐴𝑠𝑠
3-24
0.2 W kapasiteli bir güç transistörü belirtilen bir ortama sürekli ısı yaymaktadır. 24 saatte
ortama verilen ısı miktarı, direncin yüzey ısı akısı ve direncin yüzey sıcaklığının bulunması
istenmektedir.
Kabuller:
Sürekli rejim şartları mevcuttur. Isı silindirik direncin bütün yüzeylerinden uniform olarak
transfer edilmektedir.
Verilenler:
Ortam sıcaklığı, 𝑇𝑇∞ = 30℃
Direncin çapı, D=0.5 cm=0.005 m, Direncin uzunluğu, L=0.4 cm =0.004 m
Birleşik taşınım ve ışınım ısı transfer katsayısı, ℎ = 18 𝑊𝑊 ⁄𝑚𝑚2 . ℃
Sayfa 9 / 22
Hesaplamalar:
a) 24 saat boyunca dirençten ortama yayılan ısı transfer
miktarı;
𝑄𝑄 = 𝑄𝑄̇ ∆𝑡𝑡 = (0.2)(24) = 4.8 𝑊𝑊h = 0.0048 kWh
Hava
b) Direncin yüzey ısı akısı;
Güç
Silindirik yüzeyin ısı transfer yüzey alanı:
Transistörü
𝜋𝜋𝐷𝐷2
𝜋𝜋(0.005)2
𝐴𝐴𝑠𝑠 = 2
+ 𝜋𝜋𝜋𝜋𝜋𝜋 = 2
+ 𝜋𝜋(0.005)(0.004)
4
4
= 0.0001021m2
0.2
𝑄𝑄̇
=
= 1959 𝑊𝑊/𝑚𝑚2
𝑞𝑞̇ =
𝐴𝐴𝑠𝑠 0.0001021
c) Direncin yüzey sıcaklığı;
Silindirik dirençte üretilen enerji, yüzeylerden ortama taşınımla transfer edilir. Bu
durumda Newton’un soğuma kanunundan;
𝑄𝑄̇
0.2
= 30 +
= 138.8℃ bulunur.
𝑄𝑄̇ = ℎ𝐴𝐴𝑠𝑠 (𝑇𝑇𝑠𝑠 − 𝑇𝑇∞ ) → 𝑇𝑇𝑠𝑠 = 𝑇𝑇∞ +
(18)(0.0001021)
ℎ𝐴𝐴𝑠𝑠
3-33
Bir evin iki duvarında dörder adet pencere bulunurken diğer iki duvarı penceresizdir. Pencereli
ve penceresiz duvarlardaki ısı transferleri oranının bulunması istenmektedir.
Kabuller:
Duvarlardan olan ısı transferi sürekli ve tek boyutludur. Duvar ve pencelerelerin ısıl
iletkenlikleri sabittir. Işınımla olan ısı transferi ihmal edilmiştir. Taşınım ısı transfer katsayıları
evin bütün yüzeylerinde sabit ve üniformdur.
Verilenler:
Camın ısıl iletkenliği, 𝑘𝑘𝑐𝑐𝑐𝑐𝑐𝑐 = 0.78 𝑊𝑊 ⁄𝑚𝑚 . ℃
𝐿𝐿
Duvarın birim alan başına ısıl direnci, (𝑘𝑘)𝑑𝑑 = 3.3 𝑚𝑚2 . ℃/𝑊𝑊
İç yüzeydeki ısı taşınım katsayısı, ℎ𝑖𝑖 = 11 𝑊𝑊 ⁄𝑚𝑚2 . ℃
Dış yüzeydeki ısı taşınım katsayısı, ℎ𝑜𝑜 = 22 𝑊𝑊 ⁄𝑚𝑚2 . ℃
Duvarın yüksekliği 4 m, uzunluğu 12 m, genişliği 12 m.
Camın boyutu, 1m x 1.5 m, kalınlığı 6 cm=0.06 m
Hesaplamalar:
Penceresiz duvar için ısıl direnç devresi aşağıda verildiği gibi; iç ve dış ortam taşınım dirençleri
(Ri, ve Ro) ve duvarın ısıl direnci (Rd) olmak üzere birbirine seri şekilde bağlı ısıl direnç ağına
sahiptir. Toplam ısıl direnç, birbirine seri bağlı bu dirençlerin aritmetik toplamına eşittir.
Isı transfer alanı, ısı transfer yönüne dik düzlemin alanı olup değeri, 𝐴𝐴 = (4)(12) = 48 𝑚𝑚2
Isıl direnç değerleri:
Sayfa 10 / 22
Penceresiz
Duvar
𝑅𝑅𝑖𝑖 =
1
1
=
= 0.00189 ℃/𝑊𝑊
ℎ𝑖𝑖 𝐴𝐴 (11)(48)
𝑅𝑅𝑜𝑜 =
1
1
=
= 0.00095 ℃/𝑊𝑊
ℎ𝑜𝑜 𝐴𝐴 (22)(48)
𝑅𝑅𝑑𝑑 =
𝐿𝐿𝑑𝑑
𝐿𝐿 1 3.3
=� �
=
= 0.06875 ℃/𝑊𝑊
𝑘𝑘𝑑𝑑 𝐴𝐴
𝑘𝑘 𝑑𝑑 𝐴𝐴 48
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = 𝑅𝑅𝑖𝑖 + 𝑅𝑅𝑑𝑑 + 𝑅𝑅𝑜𝑜 = 0.00189 + 0.06875 + 0.00095
= 0.07159 ℃/𝑊𝑊
R𝑅𝑅i 𝑖𝑖
Penceresiz duvardan olan ısı transfer hızı;
𝑄𝑄̇𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 =
∆𝑇𝑇
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡
=
∆𝑇𝑇
= (13.97)∆𝑇𝑇
0.07159
𝑅𝑅𝑑𝑑
𝑅𝑅𝑜𝑜
Burada ∆𝑇𝑇 evin içindeki ortam sıcaklığıyla dış ortam sıcaklığı arasındaki farktır.
Pencereli duvarlarda toplam ısı transferi, pencerelerden olan iletimle ısı transferi miktarıyla bu
duvarların penceresiz kısmından olan iletimle ısı transfer miktarının toplamına eşittir.
Dolayısıyla, odanın içinden duvar-pencere kompozit yapısının iç yüzeyine olan taşınımla ısı
transferinin bir kısmı duvar üzerinden bir kısmıda cam üzerinden bu yapının diğer yüzeyine
transfer edilecektir. Bu yüzeye ulaşan toplam ısı transfer miktarıda, bu yüzeyden yine taşınımla
dış ortama aktarılacaktır. Dolayısıyla pencereli duvara ait ısıl direnç devresi aşağıdaki gibi
gösterilebilir;
𝑅𝑅𝑐𝑐𝑐𝑐𝑐𝑐
𝑅𝑅𝑖𝑖
𝑅𝑅𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑
𝑅𝑅𝑜𝑜
Pencereli bir duvarda camdan olan ısı transfer alanı;
𝐴𝐴𝑐𝑐𝑐𝑐𝑐𝑐 = 4(1 × 1.5) = 6𝑚𝑚2 (Dört adet cam bulunmakta ve camın kesit alanı 1m x 1.5m’dir)
Böylelikle, duvar-pencere kompozit yapısında duvar kısmı için ısı transfer alanı, toplam duvarpencere alanından camlı kısmın alanı çıkarılarak elde edilebilir;
𝐴𝐴𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 = 𝐴𝐴𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 − 𝐴𝐴𝑐𝑐𝑐𝑐𝑐𝑐 = 4 × 12 − 6 = 42 𝑚𝑚2 elde edilir.
Pencereli duvar için ısıl direnç devresinde iç ve dış yüzeylere ait ısıl dirençlerin değerleri
(𝑅𝑅𝑖𝑖 , 𝑅𝑅𝑜𝑜 ) pencereli duvarla aynıdır (bu ısıl dirençlere ait alanlar ve taşınım katsayıları her iki
durum içinde aynı olduğundan). Yeni durumda duvar ve cama ait ısıl direnç değerleri;
Sayfa 11 / 22
𝑅𝑅𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 =
𝑅𝑅𝑐𝑐𝑐𝑐𝑐𝑐 =
𝐿𝐿𝑑𝑑
𝐿𝐿 1
3.3
= ( )𝑑𝑑
=
= 0.07857 ℃/𝑊𝑊
𝑘𝑘 𝐴𝐴𝑑𝑑 42
𝑘𝑘𝑑𝑑 𝐴𝐴𝑑𝑑
𝐿𝐿𝑐𝑐
0.06
=
= 0.01282℃/𝑊𝑊
𝑘𝑘𝑐𝑐 𝐴𝐴𝑐𝑐 (0.78)(6)
𝑅𝑅𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 ve 𝑅𝑅𝑐𝑐𝑐𝑐𝑐𝑐 ısıl dirençleri parallel bağlı olduğu için bu ikisine ait eşdeğer ısıl direnç;
1
1
1
1
1
=
+
=
+
→ 𝑅𝑅𝑒𝑒ş = 0.01102 ℃/𝑊𝑊
𝑅𝑅𝑒𝑒ş 𝑅𝑅𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 𝑅𝑅𝑐𝑐𝑐𝑐𝑐𝑐 0.07857 0.01282
Bu durumda pencereli duvara ait ısıl direnç devresi üç direncin seri halde bağlı olduğu şekle
indirgenir.
𝑅𝑅𝑒𝑒ş
𝑅𝑅𝑖𝑖
𝑅𝑅𝑜𝑜
Duvar-pencere kompozit yapısına ait toplam ısıl direnç;
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = 𝑅𝑅𝑖𝑖 + 𝑅𝑅𝑒𝑒ş + 𝑅𝑅𝑜𝑜 = 0.00189 + 0.01102 + 0.00095 = 0.01386 ℃/𝑊𝑊
Pencereli durumdan olan ısı transfer hızı;
𝑄𝑄̇𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 =
∆𝑇𝑇
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡
=
∆𝑇𝑇
= (72.15)∆𝑇𝑇
0.01386
Burada ∆𝑇𝑇 evin içindeki ortam sıcaklığıyla dış ortam sıcaklığı arasındaki fark olup her iki
durum içinde aynıdır. Böylelikle pencereli duvardan olan ısı kaybı miktarının penceresiz
duvardan olan ısı kaybına oranı;
𝑄𝑄̇𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝
(72.15)∆𝑇𝑇
=
= 5.2 olarak bulunur.
𝑄𝑄̇𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 (13.97)∆𝑇𝑇
3-52
Yatay tuğlalardan oluşan bir duvar alçı tabakalarıyla birbirinden ayrılmış olup aynı zamanda
tuğlaların her iki yanı alçı tabakasıyla kaplanmıştır. Duvarın iç yüzeyine katı köpük kullanılarak
yalıtım yapılmıştır. Duvardan olan ısı transfer oranının bulunması istenmektedir.
Kabuller:
Duvardan olan ısı transferi sürekli ve bir boyutludur. Malzemelerin ısıl iletkenlikleri sabittir ve
ışınım etkisi gözardı edilmiştir.
Verilenler:
İç ortam sıcaklığı, 𝑇𝑇∞,1 = 22℃, Dış ortam sıcaklığı, 𝑇𝑇∞,2 = −4℃
Alçı ısıl iletkenlik değeri, 𝑘𝑘𝑎𝑎 = 0.22 W⁄m . ℃
Tuğla ısıl iletkenliği, 𝑘𝑘𝑡𝑡 = 0.72 W⁄m . ℃
Köpük ısıl iletkenliği, 𝑘𝑘𝑘𝑘 = 0.026 W⁄m . ℃
Sayfa 12 / 22
İç yüzeydeki ısı taşınım katsayısı, ℎ1 = 10 W⁄m2 . ℃
Dış yüzeydeki ısı taşınım katsayısı, ℎ2 = 20 W⁄m2 . ℃
Duvarın yüksekliği 4 m, genişliği 6 m’dir. Diğer ölçüler soruda şekil üzerinde verilmiştir.
Hesaplamalar:
Duvarın yapısı düşey doğrultuda her 33 cm’de bir tekrarlanmaktadır. Yatay doğrultuda bir
değişme yoktur. Dolayısıyla, bütün duvarı temsil ettiği için duvarın 1 m derinlik ve 0.33 m
yükseklikteki parçası alınarak hesaplamalar yapılabilir. Duvarı temsil eden kısım için ısıl direnç
devresi aşağıdaki gibi olur. Herbir ısıl direnç tek tek hesaplanırsa;
𝑅𝑅𝑜𝑜
𝑅𝑅𝑖𝑖 = 𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,1 =
𝑅𝑅1 = 𝑅𝑅𝑘𝑘ö𝑝𝑝ü𝑘𝑘 =
1
1
=
= 0.303 ℃/W
ℎ1 𝐴𝐴 (10)(0.33 × 1)
𝐿𝐿𝑘𝑘
0.02
=
= 2.33 ℃/W
𝑘𝑘𝑘𝑘 𝐴𝐴 (0.026)(0.33 × 1)
𝑅𝑅2 = 𝑅𝑅6 = 𝑅𝑅𝑎𝑎𝑎𝑎ç𝚤𝚤,𝑦𝑦𝑦𝑦𝑦𝑦 =
𝑅𝑅3 = 𝑅𝑅5 = 𝑅𝑅𝑎𝑎𝑎𝑎ç𝚤𝚤,𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 =
𝑅𝑅4 = 𝑅𝑅𝑡𝑡𝑡𝑡ğ𝑙𝑙𝑙𝑙 =
𝐿𝐿𝑎𝑎,𝑦𝑦
0.02
=
= 0.275 ℃/W
𝑘𝑘𝑎𝑎 𝐴𝐴 (0.22)(0.33 × 1)
𝐿𝐿𝑎𝑎,𝑜𝑜
0.18
=
= 54.55 ℃/W
𝑘𝑘𝑎𝑎 𝐴𝐴𝑎𝑎,𝑜𝑜 (0.22)(0.015 × 1)
𝐿𝐿𝑡𝑡
0.18
=
= 0.833 ℃/W
𝑘𝑘𝑡𝑡 𝐴𝐴𝑡𝑡 (0.72)(0.3 × 1)
𝑅𝑅𝑜𝑜 = 𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,2 =
1
1
=
= 0.152℃/W
ℎ2 𝐴𝐴 (20)(0.33 × 1)
Orta bölümde yer alan 𝑅𝑅3 , 𝑅𝑅4 ve 𝑅𝑅5 ısıl dirençleri paraleldir ve bunlara ait eşdeğer direnç;
1
𝑅𝑅𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜
=
1
1
1
1
1
1
+
+
=
+
+
→ 𝑅𝑅𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 = 0.81℃/W bulunur.
𝑅𝑅3 𝑅𝑅4 𝑅𝑅5 54.55 0.833 54.55
Bu halde bütün dirençler seri bağlıdır ve toplam direnç;
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = 𝑅𝑅𝑖𝑖 + 𝑅𝑅1 + 𝑅𝑅2 + 𝑅𝑅𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 + 𝑅𝑅6 + 𝑅𝑅𝑜𝑜 = 0.303 + 2.33 + 0.275 + 0.81 + 0.275 + 0.152
= 4.145 ℃/W bulunur.
Duvarın 0.33 m2’sinden olan ısı transfer oranı;
𝑄𝑄̇ =
𝑇𝑇∞,1 − 𝑇𝑇∞,2 [22 − (−4)]
=
= 6.27 W
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡
4.145
24 m2’lik toplam alana sahip kompozit duvardan olan ısı transferi;
𝑄𝑄̇𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = (6.27)
(4 × 6)
= 456 W olarak elde edilir.
0.33
Sayfa 13 / 22
3-55
1’er cm kalınlıklı iki alçıpan tabaka tahta dikmeler yardımıyla birbirinden 16 cm ayrılarak 12
m uzunluğunda ve 5 m yüksekliğinde bir duvar elde edilmektedir. Tahta dikmeler arası düşey
mesafe 60 cm olup ara bölge cam yünü malzeme ile kaplanmıştır. Duvarı temsil eden örnek
bölge için toplam direncin bulunması ve duvardan gerçekleşen toplam ısı transfer oranı
sorulmaktadır.
Kabuller:
Isı transferi sürekli ve bir boyutludur. Malzemelerin ısıl iletkenlik değerleri sabittir. Işınım
etkisi ihmal edilmiştir.
Verilenler:
İç ortam sıcaklığı, 𝑇𝑇∞,1 = 20℃, Dış ortam sıcaklığı, 𝑇𝑇∞,2 = −9℃
Alçıpan ısıl iletkenliği, 𝑘𝑘𝑎𝑎 = 0.17 W⁄m . ℃
Tahta dikme ısıl iletkenliği, 𝑘𝑘𝑡𝑡𝑡𝑡 = 0.11 W⁄m . ℃
Cam yünü ısıl iletkenliği, 𝑘𝑘𝑐𝑐𝑐𝑐 = 0.034 W⁄m . ℃
İç yüzeydeki ısı taşınım katsayısı, ℎ1 = 8.3 W⁄m2 . ℃
Dış yüzeydeki ısı taşınım katsayısı, ℎ2 = 34 W⁄m2 . ℃
Duvarın yüksekliği 5 m, uzunluğu 12 m’dir.
Hesaplamalar:
Duvarın yapısı aşağıda gösterilmiştir.
1 cm
16 cm
1 cm
5 cm
Cam
yünü
Alçıpan
65 cm
Alçıpan
Tahta Dikme
60 cm
Tahta Dikme
Duvarın yapısı düşey doğrultuda her 65 cm’de bir tekrarlanmaktadır. Yatay doğrultuda bir
değişme yoktur. Dolayısıyla, bütün duvarı temsil ettiği için duvarın 1 m derinlik ve 0.65 m
yükseklikteki parçası alınarak hesaplamalar yapılabilir. Kompozit duvarı temsil eden kısım için
ısıl direnç devresi aşağıdaki gibi olur. Herbir ısıl direnç tek tek hesaplanırsa;
Sayfa 14 / 22
𝑅𝑅𝑖𝑖 = 𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,1 =
1
1
=
= 0.185 ℃/W
ℎ1 𝐴𝐴 (8.3)(0.65 × 1)
𝑅𝑅1 = 𝑅𝑅4 = 𝑅𝑅𝑎𝑎𝑎𝑎ç𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤 =
𝑅𝑅2 = 𝑅𝑅𝑡𝑡𝑡𝑡ℎ𝑡𝑡𝑡𝑡 𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 =
𝑅𝑅3 = 𝑅𝑅𝑐𝑐𝑐𝑐𝑐𝑐 𝑦𝑦ü𝑛𝑛ü =
𝑅𝑅𝑜𝑜 = 𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,2 =
𝐿𝐿𝑎𝑎
0.01
=
= 0.090 ℃/W
𝑘𝑘𝑎𝑎 𝐴𝐴 (0.17)(0.65 × 1)
𝐿𝐿𝑡𝑡𝑡𝑡
0.16
=
= 29.091℃/W
𝑘𝑘𝑡𝑡𝑡𝑡 𝐴𝐴𝑡𝑡𝑡𝑡 (0.11)(0.05 × 1)
𝐿𝐿𝑐𝑐𝑐𝑐
0.16
=
= 7.843 ℃/W
𝑘𝑘𝑐𝑐𝑐𝑐 𝐴𝐴𝑐𝑐𝑐𝑐 (0.034)(0.6 × 1)
1
1
=
= 0.045℃/W
ℎ2 𝐴𝐴 (34)(0.65 × 1)
Orta bölümde yer alan 𝑅𝑅2 ,ve 𝑅𝑅3 ısıl dirençleri birbirine paraleldir ve bunlara ait eşdeğer direnç;
1
𝑅𝑅𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜
=
1
1
1
1
+
=
+
→ 𝑅𝑅𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 = 6.178℃/W bulunur.
𝑅𝑅2 𝑅𝑅3 29.091 7.843
Bu durumda bütün dirençler seri bağlıdır ve toplam direnç;
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = 𝑅𝑅𝑖𝑖 + 𝑅𝑅1 + 𝑅𝑅𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 + 𝑅𝑅4 + 𝑅𝑅𝑜𝑜 = 0.185 + 0.090 + 6.178 + 0.090 + 0.045
= 6.588 ℃/W bulunur. (0.65 m × 1m′lik kesit için)
Duvarın 0.65 m2’sinden olan ısı transfer oranı;
𝑄𝑄̇ =
𝑇𝑇∞,1 − 𝑇𝑇∞,2 [20 − (−9)]
=
= 4.40 W
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡
6.588
60 m2’lik toplam alana sahip kompozit duvardan olan ısı transferi;
𝑄𝑄̇𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = (4.40)
3-56
(12 × 5)
= 406 W olarak elde edilir.
0.65
Bir kompozit duvar, dolu tuğlalardan veya üzerinde dokuz adet kare hava deliği bulunan hava
delikli tuğlalardan yapılacaktır. Bitişik tuğlalar arasında ve bunları çevreleyen dört yüzey
arasında alçı tabakası bulunmaktadır. Duvarın dolu tuğlalardan ve delikli tuğlalardan yapılması
durumunda gerçekleşecek ısı transfer hızının bulunması istenmektedir.
Kabuller:
Isı transferi sürekli ve bir boyutludur. Malzemelerin ısıl iletkenlik değerleri sabittir. Işınım
etkisi ihmal edilmiştir.
Verilenler:
İç ortam sıcaklığı, 𝑇𝑇∞,1 = 27℃, Dış ortam sıcaklığı, 𝑇𝑇∞,2 = 0℃
Sayfa 15 / 22
Dolu tuğla ısıl iletkenliği, 𝑘𝑘𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 = 0.70 W⁄m . ℃
Delikli tuğla ısıl iletkenliği, 𝑘𝑘𝑑𝑑𝑑𝑑𝑑𝑑𝑖𝑖𝑘𝑘𝑘𝑘𝑘𝑘 = 0.026 W⁄m . ℃
Alçı ısıl iletkenliği, 𝑘𝑘𝑎𝑎 = 0.17 W⁄m . ℃
İç yüzeydeki ısı taşınım katsayısı, ℎ1 = 9 W⁄m2 . ℃
Dış yüzeydeki ısı taşınım katsayısı, ℎ2 = 23 W⁄m2 . ℃
Kompozit duvarın yüksekliği 3 m, uzunluğu 9 m’dir.
Hesaplamalar:
Duvarın yapısı hem düşey düşey doğrultuda hemde genişlik doğrultusunda her 19 cm’de bir
tekrarlanmaktadır. Dolayısıyla, bütün duvarı temsil ettiği için duvarın 0.19 m derinlik ve 0.19
m yükseklikteki parçası alınarak hesaplamalar yapılabilir. Dolu tuğlalardan yapılmış duvar için
örnek kısmın ısıl direnç devresi aşağıdaki gibi olur. Herbir ısıl direnç tek tek hesaplanırsa;
(a) Dolu tuğlalardan yapılmış duvar için;
𝑅𝑅𝑖𝑖 = 𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,1 =
1
1
=
= 3.078 ℃/W
ℎ1 𝐴𝐴 (9)(0.19 × 0.19)
𝑅𝑅1 = 𝑅𝑅5 = 𝑅𝑅𝑎𝑎𝑎𝑎ç𝚤𝚤,1 =
𝑅𝑅2 = 𝑅𝑅𝑎𝑎𝑎𝑎ç𝚤𝚤,2 =
𝑅𝑅3 = 𝑅𝑅𝑎𝑎𝑎𝑎ç𝚤𝚤,3 =
𝐿𝐿𝑎𝑎,1
0.01
=
= 1.629 ℃/W
𝑘𝑘𝑎𝑎 𝐴𝐴 (0.17)(0.19 × 0.19)
𝐿𝐿𝑎𝑎,2
0.23
=
= 712 ℃/W
𝑘𝑘𝑎𝑎 𝐴𝐴𝑎𝑎,2 (0.17)(0.01 × 0.19)
𝐿𝐿𝑎𝑎,3
0.23
=
= 751.6 ℃/W
𝑘𝑘𝑎𝑎 𝐴𝐴𝑎𝑎,3 (0.17)(0.01 × 0.18)
𝑅𝑅4 = 𝑅𝑅𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 𝑡𝑡𝑡𝑡ğ𝑙𝑙𝑙𝑙 =
𝑅𝑅𝑜𝑜 = 𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,2 =
𝐿𝐿𝑡𝑡
0.23
=
= 10.14 ℃/W
𝑘𝑘𝑡𝑡 𝐴𝐴𝑡𝑡 (0.70)(0.18 × 0.18)
1
1
=
= 1.204 ℃/W
ℎ2 𝐴𝐴 (23)(0.19 × 0.19)
Orta bölümde yer alan 𝑅𝑅2 , 𝑅𝑅3 ve 𝑅𝑅4 ısıl dirençleri birbirine paraleldir ve bunlara ait eşdeğer
direnç;
1
𝑅𝑅𝑜𝑜𝑟𝑟𝑟𝑟𝑟𝑟
=
1
1
1
1
1
1
+
+
=
+
+
→ 𝑅𝑅𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 = 9.87℃/W bulunur.
𝑅𝑅2 𝑅𝑅3 𝑅𝑅4 712 751.6 10.14
Bu durumda bütün dirençler seri bağlıdır ve toplam direnç;
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = 𝑅𝑅𝑖𝑖 + 𝑅𝑅1 + 𝑅𝑅𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 + 𝑅𝑅5 + 𝑅𝑅𝑜𝑜 = 3.078 + 1.629 + 9.87 + 1.629 + 1.204
= 17.41 ℃/W bulunur. (0.19 m × 0.19 m = 0.0361 𝑚𝑚2 ′lik kesit için)
Sayfa 16 / 22
Dolu tuğlalardan yapılmış duvarın 0.0361 m2’sinden olan ısı transfer oranı;
𝑄𝑄̇ =
𝑇𝑇∞,1 − 𝑇𝑇∞,2 27 − 0
=
= 1.55W
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡
17.41
9 m × 3 m = 27m2 toplam alana sahip dolu tuğladan imal edilmiş kompozit duvardan olan ısı
transferi;
𝑄𝑄̇𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = (1.55)
(9 × 3)
= 1159 W olarak elde edilir.
0.0361
(b) Hava delikli tuğlalardan yapılmış duvar için hesaplamalar
Bu durum için ısıl direnç ağı aşağıdaki gibi olur. Dolu tuğlalı duvara ait ısıl direnç ağından
farklı olarak paralel bağlı direnç grubunda, tuğla içerisindeki durgun havaya ait ısıl direnç
mevcuttur. Bu durumda ısıl direnç değerleri;
Hava delikli tuğlanın kesit alanı 18cm x 18cm olup, içerisinde 9 adet 4cm x 4cm kare kesitli
hava kanalı bulunur. Dolayısıyla hava deliklerinin ve tuğlanın alanları;
𝐴𝐴ℎ𝑎𝑎𝑎𝑎𝑎𝑎 = (9)(0.04 × 0.04) = 0.0144 m2
𝐴𝐴𝑡𝑡𝑡𝑡ğ𝑙𝑙𝑙𝑙 = (0.18 × 0.18) − 0.0144 = 0.018 m2 bulunur.
Bu durumda hava delikli tuğlanın hava ve tuğla kısımlarına ait ısıl direnç değerleri;
𝑅𝑅4 = 𝑅𝑅ℎ𝑎𝑎𝑎𝑎𝑎𝑎 =
𝑅𝑅5 = 𝑅𝑅𝑡𝑡𝑡𝑡ğ𝑙𝑙𝑙𝑙 =
𝐿𝐿ℎ
0.23
=
= 614.3 ℃/W
𝑘𝑘ℎ 𝐴𝐴ℎ𝑎𝑎𝑎𝑎𝑎𝑎 (0.026)(0.0144)
𝐿𝐿𝑡𝑡
0.23
=
= 18.3 ℃/W
𝑘𝑘𝑡𝑡 𝐴𝐴𝑡𝑡𝑡𝑡ğ𝑙𝑙𝑙𝑙 (0.70)(0.018)
Orta bölümde yer alan 𝑅𝑅2 , 𝑅𝑅3 , 𝑅𝑅4 ve 𝑅𝑅5 ısıl dirençleri birbirine paraleldir ve bunlara ait eşdeğer
direnç;
1
𝑅𝑅𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜
=
1
1
1
1
1
1
1
1
+
+
+
=
+
+
+
→ 𝑅𝑅𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 = 16.9℃/W bulunur.
𝑅𝑅2 𝑅𝑅3 𝑅𝑅4 𝑅𝑅5 712 751.6 614.3 18.3
Bu durumda bütün dirençler seri bağlı hale gelir ve toplam direnç;
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = 𝑅𝑅𝑖𝑖 + 𝑅𝑅1 + 𝑅𝑅𝑜𝑜𝑜𝑜𝑜𝑜𝑜𝑜 + 𝑅𝑅6 + 𝑅𝑅𝑜𝑜 = 3.078 + 1.629 + 16.9 + 1.629 + 1.204
= 24.44 ℃/W bulunur. (0.19 m × 0.19 m = 0.0361 𝑚𝑚2 ′lik kesit için)
Hava delikli tuğlalardan yapılmış duvarın 0.0361 m2’sinden olan ısı transfer oranı;
Sayfa 17 / 22
𝑄𝑄̇ =
𝑇𝑇∞,1 − 𝑇𝑇∞,2 27 − 0
=
= 1.1W
24.44
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡
9 m × 3 m = 27m2 toplam alana sahip hava delikli tuğladan imal edilmiş kompozit duvardan
olan ısı transferi;
𝑄𝑄̇𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = (1.1)
3-57
(9 × 3)
= 822.7 W olarak elde edilir.
0.0361
Sağ ve sol yüzeyleri uniform belirli bir sıcaklık değerinde tutulan yatay ve düşey katmanlardan
oluşan kompozit bir duvardan olan ısı transferi miktarı arayüzey sıcaklık değerleri ve F
kısmında meydana gelen sıcaklık düşüşü sorulmaktadır.
Kabuller:
Isı tarnsferi sürekli ve bir boyutludur. Malzemelerin ısıl dirençleri sabittir. Arayüzeylerdeki
temas dirençleri ihmal edilmiştir.
Verilenler:
A, B, C, D, E ve F katmanlarına ait ısıl iletkenlik değerleri sırasıyla;
𝑘𝑘𝐴𝐴 = 2 W⁄m . ℃,
𝑘𝑘𝐵𝐵 = 8 W⁄m . ℃,
𝑘𝑘𝐶𝐶 = 20 W⁄m . ℃,
𝑘𝑘𝐸𝐸 = 35 W⁄m . ℃, 𝑘𝑘𝐹𝐹 = 2𝑘𝑘𝐸𝐸 = 2 W⁄m . ℃,
A yüzeyinin sıcaklığı, 𝑇𝑇1 = 300 ℃,
𝑘𝑘𝐷𝐷 = 15 W⁄m . ℃,
F yüzeyinin sıcaklığı, 𝑇𝑇2 = 100℃
Duvarın yüksekliği 5 m, uzunluğu 8 m’dir.
Hesaplamalar:
Soruda verilen kompozit duvara ait ısıl direnç devresi aşağıda verilmiştir.
′
Kompozit duvara temsilen 𝐴𝐴 = 0.12 × 1 = 0.12 m2 lik kısmı alarak hesaplamalar yapılırsa
ısıl direnç değerleri;
𝑅𝑅1 = 𝑅𝑅𝐴𝐴 = (
𝐿𝐿
0.01
)𝐴𝐴 =
= 0.042 ℃/W
𝑘𝑘𝑘𝑘
2 × 0.12
𝑅𝑅2 = 𝑅𝑅4 = 𝑅𝑅𝐶𝐶 = (
𝑅𝑅3 = 𝑅𝑅𝐵𝐵 = (
𝐿𝐿
0.05
)𝐶𝐶 =
= 0.063 ℃/W
𝑘𝑘𝑘𝑘
20 × 0.04
𝐿𝐿
0.05
)𝐵𝐵 =
= 0.156 ℃/W
𝑘𝑘𝑘𝑘
8 × 0.04
Sayfa 18 / 22
𝑅𝑅5 = 𝑅𝑅𝐷𝐷 = (
𝑅𝑅6 = 𝑅𝑅𝐸𝐸 = (
𝑅𝑅7 = 𝑅𝑅𝐹𝐹 = (
𝐿𝐿
0.1
)𝐷𝐷 =
= 0.111 ℃/W
𝑘𝑘𝑘𝑘
15 × 0.06
𝐿𝐿
0.1
)𝐸𝐸 =
= 0.048 ℃/W
𝑘𝑘𝑘𝑘
35 × 0.06
𝐿𝐿
0.06
)𝐹𝐹 =
= 0.25 ℃/W
𝑘𝑘𝑘𝑘
2 × 0.12
Paralel bağlı ısıl dirençlere ait eşdeğer ısıl direnç değerleri;
1
𝑅𝑅𝑒𝑒ş,1
1
𝑅𝑅𝑒𝑒ş,2
=
=
1
1
1
1
1
1
+
+
=
+
+
→ 𝑅𝑅𝑒𝑒ş,1 = 0.026 ℃/W
𝑅𝑅2 𝑅𝑅3 𝑅𝑅4 0.063 0.156 0.063
1
1
1
1
+
=
+
→ 𝑅𝑅𝑒𝑒ş,2 = 0.034 ℃/W
𝑅𝑅5 𝑅𝑅6 0.111 0.048
Bu durumda ısıl direnç ağı birbirine seri bağlı ısıl dirençlerden oluşur ve toplam direnç;
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = 𝑅𝑅1 + 𝑅𝑅𝑒𝑒ş,1 + 𝑅𝑅𝑒𝑒ş,2 + 𝑅𝑅7 = 0.042 + 0.026 + 0.034 + 0.25 = 0.352 ℃/W olur.
Duvarın 0.12 m2’yüzey alanından olan ısı transferi;
𝑄𝑄̇ =
𝑇𝑇1 − 𝑇𝑇2 300 − 100
=
= 568.2 W
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡
0.352
Duvarın bütün yüzeyinden olan ısı transfer oranı;
𝑄𝑄̇𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = 568.2
(5 × 8)
= 1.9 × 105 W
0.12
(b) B, D ve E yüzeylerinin birleştiği noktanın sıcaklığı;
A katmanının sol yüzeyiyle, B, D ve E katmanlarının sağ yüzeyi arasındaki toplam ısıl direnç
yazılırsa;
𝑅𝑅𝑇𝑇 = 𝑅𝑅1 + 𝑅𝑅𝑒𝑒ş,1 = 0.042 + 0.026 = 0.068 ℃/W
Dolayısıyla istenen yüzeydeki sıcaklık değeri;
𝑄𝑄̇ =
𝑇𝑇1 − 𝑇𝑇
→ 𝑇𝑇 = 𝑇𝑇1 − 𝑄𝑄̇ 𝑅𝑅𝑡𝑡 = 300 − (568.2)(0.068) = 261.3℃ elde edilir.
𝑅𝑅𝑡𝑡
𝑄𝑄̇ =
∆𝑇𝑇
→ ∆𝑇𝑇 = 𝑄𝑄̇ 𝑅𝑅𝐹𝐹 = (568.2)(0.25) = 142℃ bulunur.
𝑅𝑅𝐹𝐹
(c) F katmanı boyunca meydana gelen sıcaklık düşüşü;
3-69
Buzlu suyla doldurulmuş bir küresel tankın dış yüzeyinde taşınım ve ışınımla ısı transferi
olmaktadır. Isı transfer hızı ve bir günde eriyecek buz miktarı sorulmaktadır.
Kabuller:
Sınırlarda tanımlı ısıl şartlar zamanla değişmediği için ısı transferi süreklidir. Merkeze göre ısıl
simetri olduğu için ısı transferi tek boyutludur. Isıl iletkenlikler sabittir.
Sayfa 19 / 22
Verilenler:
0 oC’de buzlu su, 𝑇𝑇∞,1 = 0℃, Dış ortam sıcaklığı, 𝑇𝑇∞,2 = 25℃
Çeliğin ısıl iletkenliği, 𝑘𝑘ç = 15 W⁄m . ℃
Atmosfer basıncındaki suyun erime ısısı, ℎ𝑖𝑖𝑖𝑖 = 333.7 kJ/kg
İç yüzeydeki ısı taşınım katsayısı, ℎ𝑖𝑖 = 80 W⁄m2 . ℃
Dış yüzeydeki ısı taşınım katsayısı, ℎ𝑑𝑑 = 10 W⁄m2 . ℃
Küresel tankın iç çapı, 𝐷𝐷𝑖𝑖 = 8 m ve kalınlığı, 𝑡𝑡 = 1.5 cm
Küresel tankın dış çapı, 𝐷𝐷𝑑𝑑 = 𝐷𝐷𝑖𝑖 + 2 × 𝑡𝑡 = 8 + (2)(0.015) = 8.03 m
Tankın dış yüzeyinin yayıcılığı, 𝜀𝜀 = 1
Stefan-Boltzmann sabiti, 𝜎𝜎 = 5.67 × 10−8 W⁄m2 . K 4
Hesaplamalar:
Probleme ait ısıl direnç ağı aşağıdaki gibidir.
Tankın iç ve dış yüzey alanları;
𝐴𝐴𝑖𝑖 = 𝜋𝜋𝐷𝐷𝑖𝑖2 = 𝜋𝜋(8)2 = 201.06 m2
𝐴𝐴𝑑𝑑 = 𝜋𝜋𝐷𝐷𝑑𝑑2 = 𝜋𝜋(8.03)2 = 202.57 m2
Işınım ısı transfer katsayısı,
2
ℎ𝚤𝚤ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤 = 𝜀𝜀𝜀𝜀(𝑇𝑇22 + 𝑇𝑇∞,2
)(𝑇𝑇2 + 𝑇𝑇∞,2 )
bağıntısından bulunur. Fakat tankın dış yüzey sıcaklığı (𝑇𝑇2 ) bilinmediğinden dolayı ℎ𝚤𝚤ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤
değerini hesaplamak için ilk başta 𝑇𝑇2 değeri kabul edelir ve daha sonra bu kabulun hassasiyeti
kontrol edilir. Tankın içerisindeki ısı transfer katsayısı çok büyük olduğundan 𝑇𝑇2 sıcaklığının
0oC’ye daha yakın olması beklenir. 𝑇𝑇2 = 4℃ = 277 K alınarak ışınım ısı transfer katsayısı;
ℎ𝚤𝚤ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤 = (1)(5.67 × 10−8 )(2772 + 2982 )(277 + 298) = 5.398 W⁄m2 . K olarak bulunur.
Isıl direnç değerleri;
𝑅𝑅𝑖𝑖 = 𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,1 =
𝑅𝑅1 = 𝑅𝑅𝑘𝑘ü𝑟𝑟𝑟𝑟 =
1
1
=
= 0.000062 ℃/W
ℎ𝑖𝑖 𝐴𝐴𝑖𝑖 (80)(201.06)
𝑟𝑟2 − 𝑟𝑟1
4.015 − 4
=
= 0.000005 ℃/W
4𝜋𝜋𝜋𝜋𝑟𝑟1 𝑟𝑟2 4𝜋𝜋(15)(4.015)(4)
Sayfa 20 / 22
𝑅𝑅𝑜𝑜 = 𝑅𝑅𝑡𝑡𝑡𝑡ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤,2 =
𝑅𝑅𝑟𝑟𝑟𝑟𝑟𝑟 = 𝑅𝑅𝚤𝚤ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤 =
1
1
=
= 0.000494 ℃/W
ℎ𝑑𝑑 𝐴𝐴𝑑𝑑 (10)(202.57)
1
ℎ𝚤𝚤ş𝚤𝚤𝚤𝚤𝚤𝚤𝚤𝚤 𝐴𝐴𝑑𝑑
=
1
= 0.000915 ℃/W
(5.398)(202.57)
𝑅𝑅𝑜𝑜 ve 𝑅𝑅𝑟𝑟𝑟𝑟𝑟𝑟 iki paralel direncin yerine eşdeğer direnç hesaplanırsa;
1
𝑅𝑅𝑒𝑒ş𝑑𝑑𝑑𝑑ğ𝑒𝑒𝑒𝑒
=
1
1
1
1
+
=
+
→ 𝑅𝑅𝑒𝑒ş𝑑𝑑𝑑𝑑ğ𝑒𝑒𝑒𝑒 = 0.000321 ℃/W
𝑅𝑅o 𝑅𝑅rad 0.000494 0.000915
Bu durumda bütün dirençler seridir ve toplam direnç;
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡 = 𝑅𝑅𝑖𝑖 + 𝑅𝑅1 + 𝑅𝑅𝑒𝑒ş𝑑𝑑𝑑𝑑ğ𝑒𝑒𝑒𝑒 = 0.000062 + 0.000005 + 0.000321 = 0.000388 ℃/W
olarak bulunur. Buzlu suya aktarılan sürekli ısı transfer hızı ise;
𝑄𝑄̇ =
𝑇𝑇∞,2 − 𝑇𝑇∞,1
25 − 0
=
= 64433 W olur.
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡
0.000388
𝑄𝑄̇ =
𝑇𝑇∞,2 − 𝑇𝑇2
=→ 𝑇𝑇2 = 𝑇𝑇∞,2 − 𝑄𝑄̇ 𝑅𝑅𝑒𝑒ş𝑑𝑑𝑑𝑑ğ𝑒𝑒𝑒𝑒 = 25 − (64433)(0.000321) = 4.3 ℃
𝑅𝑅𝑒𝑒ş𝑑𝑑𝑑𝑑ğ𝑒𝑒𝑒𝑒
Başlangıçta kabul edilen 𝑇𝑇2 değerinin geçerliliğini control etmek için dış yüzey sıcaklığı;
olarak elde edilir. Bu değer ışınım ısı transfer katsayısının bulunmasında kabul edilen 4 oC’ye
yakındır. Dolayısıyla, 𝑇𝑇2 değerini 4.3 oC alarak hesaplamaların tekrarlanmasına gerek yoktur.
(b) 24 saatlik sürede gerçekleşen toplam ısı transfer miktarı;
𝑄𝑄 = 𝑄𝑄̇ ∆𝑡𝑡 = (64433)(24 × 3600) = 5.567 × 106 kJ
0 oC’deki buzun eriyebilmesi için 333.7 kJ enerji gerektiğine göre 24 saatlik periyotta eriyecek
buz kütlesi;
𝑚𝑚𝑏𝑏𝑏𝑏𝑏𝑏
3-70
𝑄𝑄
5.567 × 106
=
=
= 16683 kg buz erir.
ℎ𝑖𝑖𝑖𝑖
333.7
Cam yünü yalıtımla kaplanmış bir buhar borusunun yüzeylerinde taşınımla ısı transferi
olmaktadır. Birim uzunluktaki ısı transfer hızı ile boru ve yalıtım üzerindeki sıcaklık düşüş
değerlerinin bulunması istenmektedir.
Kabuller:
Zamana bağlı herhangi bir değişim olmadığından ısı transferi süreklidir. Eksene göre ısıl simetri
olup eksenel doğrultuda değişim olmadığından ısı transferi bir boyutludur. Isıl iletkenlikler
sabittir. Arayüzeyde ısıl temas direnci ihmal edilmiştir.
Verilenler:
Silindir içinden akan buharın sıcaklığı, 𝑇𝑇∞,1 = 320℃, Dış ortam sıcaklığı 𝑇𝑇∞,2 = 5℃
Çeliğin ısıl iletkenlik değeri, 𝑘𝑘ç = 15 W⁄m . ℃
Sayfa 21 / 22
Cam yünü ısıl iletkenliği, 𝑘𝑘𝑐𝑐𝑐𝑐 = 0.038 W⁄m . ℃
Boru içerisindeki ısı transfer katsayısı, ℎ𝑖𝑖 = 80 W⁄m2 . ℃
Birleşik doğal taşınım ve ışınım ısı transfer katsayısı, ℎ𝑜𝑜 = 15 W⁄m2 . ℃
Silindirin iç çapı, 𝐷𝐷𝑖𝑖 = 5 cm = 0.05 m
Silindirin dış çapı, 𝐷𝐷2 = 5.5 cm = 0.055 m
Cam yünü yalıtım kalınlığı, t=3 cm=0.03 m
Yalıtım dış çapı, 𝐷𝐷𝑜𝑜 = 𝐷𝐷2 + 2 × 𝑡𝑡 = 0.055 + 2 × 0.03 = 0.115 m
Hesaplamalar:
Isıl direnç ağı aşağıda gösterildiği gibi seri bağlı dört adet ısıl dirençten oluşmaktadır. Silindirik
borunun uzunluğu L=1 m alınıp taşınıma maruz yüzey alanları:
𝐴𝐴𝑖𝑖 = 2𝜋𝜋𝑟𝑟1 𝐿𝐿 = 2𝜋𝜋(0.025 × 1) = 0.157 m2
𝐴𝐴𝑜𝑜 = 2𝜋𝜋𝑟𝑟3 𝐿𝐿 = 2𝜋𝜋(0.0575 × 1) = 0.361 m2
olarak hesaplanır. Her bir ısıl direnç:
1
1
=
= 0.08 ℃/W
ℎ𝑖𝑖 𝐴𝐴𝑖𝑖 (80)(0.157)
𝑅𝑅𝑖𝑖 =
𝑅𝑅1 = 𝑅𝑅𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏 =
ln(𝑟𝑟2 ⁄𝑟𝑟1 ) ln(0.0275⁄0.025)
=
= 0.00101 ℃/W
2𝜋𝜋(15)(1)
2𝜋𝜋𝑘𝑘ç 𝐿𝐿
𝑅𝑅2 = 𝑅𝑅𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦 =
𝑅𝑅𝑜𝑜 =
ln(𝑟𝑟3 ⁄𝑟𝑟2 ) ln(0.0575⁄0.0275)
=
= 3.089 ℃/W
2𝜋𝜋𝑘𝑘𝑐𝑐𝑐𝑐 𝐿𝐿
2𝜋𝜋(0.038)(1)
1
1
=
= 0.1847 ℃/W
ℎ𝑜𝑜 𝐴𝐴𝑜𝑜 (15)(0.361)
Bütün dirençler seri bağlı oldukları için toplam direnç:
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑚𝑚 = 𝑅𝑅𝑖𝑖 + 𝑅𝑅1 + 𝑅𝑅2 + 𝑅𝑅𝑜𝑜 = 0.08 + 0.00101 + 3.089 + 0.1847 = 3.355 ℃/W
bulunur. Bu durumda buhardan sürekli ısı kaybı:
𝑄𝑄̇ =
𝑇𝑇∞,1 − 𝑇𝑇∞,2 320 − 5
=
= 93.9 W
𝑅𝑅𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡𝑡
3.355
Boru ve yalıtım içerisindeki sıcaklık düşüş miktarları:
∆𝑇𝑇𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏 = 𝑄𝑄̇ 𝑅𝑅𝑏𝑏𝑏𝑏𝑏𝑏𝑏𝑏 = (93.9)(0.00101) = 0.095 ℃
∆𝑇𝑇𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦 = 𝑄𝑄̇ 𝑅𝑅𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦𝑦 = (93.9)(3.089) = 290℃ olarak elde edilir.
Sayfa 22 / 22