ÇÖZÜMLÜ SORULAR
SORU 2.1
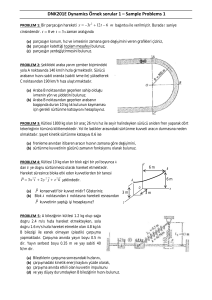
Arabadaki benzin deposunun yakıt göstergesi şekildeki gibi, tabanındaki basınç ölçerle
orantılı değerler gösterir. Depo 30 cm derinliğinde ise ve içine yanlışlıkla konulmuş 2 cm
yüksekliğinde su ve üzerinde benzin içeriyorsa gösterge tam dolu olduğunu gösterdiğinde
deponun üzerinde kalan havanın yüksekliği nedir ?
ÇÖZÜM
γBenzin = 6670 N / m3 olmak üzere ;
Depo tamamen dolu durumda iken mevcut basınç ;
Pgös = ( γBenzin ).h = ( 6670 N / m3 ). ( 0.3 m) = 2001 N / m2
Deponun altında su varken basınç değişmiyor. Buna göre hava sütunu yüksekliği ;
2001 ( 9790 . 0 , 02 ) 6670 .( 0 , 28 h ) (11 ,8 * h ) h 0 , 0094 m
SORU 2.2
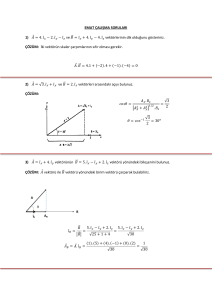
Şekilde gösterilen düzenekte pistonu itmek için D noktasından uygulanması gereken kuvveti
hesaplayınız?
ÇÖZÜM
445 N’luk kuvvetin C pistonuna etkisi bulunmalıdır. Bunun için E noktasına göre moment
alınırsa;
F C . 100 445 . 200 F C 890 N
D noktasından uygulanması gereken kuvveti bulmak için küçük ve büyük piston arasındaki
ilişki kullanılırsa ;
FC
F
FD
890 N
D
F D 22250 N
2
AC
AD
. 0 , 05
. 0 , 25 2
4
4
1
SORU 2.3
Şekildeki hidrolik kaldırıcı 8797,6 N / m3 özgül ağırlığındaki yağ ile doludur. İki pistonun
ağırlığını ihmal ederek, bu tasarım için 8896 N’luk bir ağırlığı desteklemek için gerekli olan
basma kuvveti F ne kadardır ?
ÇÖZÜM
Büyük piston için ;
W
8896
P
A .0 ,0762
2
1950720 ( N / m 2 ) 1950 ,72 kPa
4
Bu değer küçük pistona uygulanacak basınçla orantılı olduğundan ;
P p . A kucuk P 1950 , 72 .
. 0 , 0254
2
4
P 0 , 988 N
A noktasına göre moment alınırsa ;
F.( 0,381 0,0254 ) 0,988. 0,0254
F 0,0623 kN 62,3 N
bulunur.
SORU 2.4
Şekildeki sistemde A ve B borularındaki basınçların farkı ikisi arasına yerleştirilmiş civalı bir
diferansiyel manometre ile tespit edilmektedir.
γ1 = 1000 N/m3 ve γ2 = 13600 N/ m3, h= 0,5m, a=1,5m, b=0,75 m,
olduğuna göre A ve B boruları arasındaki basınç fakını bulunuz?
2
ÇÖZÜM
A noktasından başlayarak aynı ortamda yatay düzlemde basıncın değişmediği ve aşağıya
inildikçe basıncın derinlikle doğru orantılı olarak arttığı prensibi hatırlanırsa;
PA a. 1 h. 2 (b h). 1 PB
PA PB 0,5.13600 (0,25.1000) (1,5.1000) 5550 N / m 2
bulunur.
SORU 2.5
Şekildeki sistemde sıcaklık 20 ºC’ dir. Atmosfer basıncı 101,33 kPa ve tankın dibindeki
basınç 242 kPa ise X akışkanının özgül ağırlığı nedir ?
ÇÖZÜM
γSAE 30 = 8720 N / m3
γsu = 9790 N / m3
γciva = 133100 N / m3 olmak üzere ;
Pa SAE 30 .(1m ) su .( 2 m ) x .(3m ) civa .( 0,5m )
denkleminde özgül ağırlık değerleri yerine yazılırsa sonuç ;
γx = 15275 N / m3 bulunur.
SORU 2.6
Aşağıdaki şekilde gösterilen tank 20 0C sıcaklıkta hava ve yağ içermektedir. Yağın
yoğunluğu 898 kg/m3 ve suyun yoğunluğu 998 kg/m3 olduğuna göre ‘h’ değerini bulunuz?
ÇÖZÜM
Patm (898)( g )(h 0.12) (998)( g )(0.06 0.12) Patm
h 0.08m 8cm
3
SORU 2.7
Su boru içerisinde yukarıya doğru 300 ’lik bir açıyla akmaktadır. Civa manometresinden,
h=12cm okunmaktadır. Boru içersinde, (1) ve (2) noktaları arasındaki basınç değişimini
belirleyiniz?
Not: Civanın özgül ağırlığı 133100 N/m3 ve suyun özgül ağırlığı 9790 N/m3.
ÇÖZÜM
P1 9790h 133100h 9790(tan 30)(2) P2
P1 P2 26100 Pa
SORU 2.8
Şekilde gösterilen her iki tank ve eğik tüp atmosfere açıktır. L=2.13m ise eğik borunun
açısının bulunabileceği denklemi yazınız?
ÇÖZÜM
Pa (0.8)(9790)(0.5) (9790)(0.5) 9790(2.13 sin ) Pa
denkleminden açı değeri bulunabilir.
SORU 2.9
Şekilde gösterilen AB kapısı 5 m genişliğindedir. A menteşeyle,
tarafından engellenmektedir.
a) B noktasındaki durdurma kuvveti belirleyiniz?
b) h=9.5 m iken A noktasındaki tepki kuvvetini bulunuz?
4
B noktası bir kütük
ÇÖZÜM
AB nin merkez noktası 2 m dir. Merkezden itibaren suyun üstündeki nokta arasındaki mesafe
9.5-2=7.5 m dir. Kapıdaki toplam hidrostatik kuvvet,
F hCG Akapı (998)(9.81)(7.5)(20) 1468557 N 1468.6kN
I xx sin
(1 / 12)(5)(4) 3 sin 90 0
0.178m
hCG A
7.5(20)
Bx kuvveti için A noktasına göre moment alınırsa,
y CP
M
A
B x (4) (1468.6kN )(2.178) 0
B x 799,65kN
A noktasındaki tepki
Fx 0 1468.6 799,65 Ax 0 Ax 848,95kN
F
x
0 Az Wkapı Az
Az 0
SORU 2.10
Şekildeki kapak 1,524 m genişliğinde olup B noktasından mafsallı ve A noktasında bir düz
duvara dayalıdır. Buna göre ;
a) Deniz suyu basıncından dolayı kapağa gelen kuvveti hesaplayınız?
b) A noktasında duvar tarafından uygulanan yatay kuvvet P’yi hesaplayınız?
c) B mafsalındaki reaksiyon kuvvetlerini bulunuz?
5
ÇÖZÜM
a)
Kapak Alanı : ( 1,524 m).( 3,048 m) = 4,645 m2
AB 1,824 2 2,438 2 3,048m
Geometriden A’dan B’ye kadar kapağın uzunluğu 3,048 m’dir ve ağırlık merkezi iki
noktanın arasında tam ortadadır ( yani B nok. 0,914 m ) üstündedir. Buna göre ağırlık
merkezinin derinliği ;
h AM 4,572 0,914 3,658m
Kapağın her iki yüzüne etki ettiğinden Pa dikkate alınmayabilir. Kapağın üzerine etkiyen
hidrostatik kuvvet ;
F PAM . A .h AM . A (10054 N / m 3 ).(3,658m).(4,645m 2 ) 170838.43 N
b)
Öncelikle F kuvvetinin basınç merkezini bulmalıyız. Kapağın serbest cisim diyagramı
şekilde gösterilmiştir. Kapak bir dikdörtgendir. Bu nedenle ;
Ixy = 0 ve I xx
b.L3 1,524.3,0483
3,596m 4
12
12
AM’den BM’ye kadar olan l mesafesi, Pa basıncı dikkate alınmadığı için ;
I . sin
l y BM xx
0,127 m
h AM . A
B noktasından F kuvvetinin etkidiği noktaya olan mesafe böylece ( 3,048 – 0,127 – 1,524)
1,397 m olur.
B noktası etrafındaki moment ;
P.L.Sin F 1,524 l P.1,828 170838,43
. 1,397
P = 130558,69 N bulunur.
F ve P kuvvetleri bilindiğine göre Bx ve Bz ;
Fx Bx F .Sin P Bx 28055,63N
Fz 0 Bz F .Cos Bz 136670,74 N
bulunur.
6
SORU 2.11
Şekilde gösterildiği gibi AB kapısı 1 m genişliğindedir.(Gliserin 12.36kN / m 3 )
a) Net Hidrostatik kuvveti bulunuz?
b) Oluşan kuvvetin B noktasından yüksekliğini bulunuz?
ÇÖZÜM
a)
2
FH 2 0 (9.79)(1.8 1.2 )(2)(1) 78.32kN
2
2
FGls (12.36)(1.2 )(2)(1) 54.38kN
2
Fnet FH 2O FGls 78.32 54.38 23.94kN
b)
y cp
I xx sin
hcg A
90
ycp H O 1.8112.2 /((122 /)2sin
0.0833m
) 21
3
0
2
y
cp gls
M
B
12 /(12) sin 90 0
0.01515m
1.2 (2 / 2) 21
3
0 78.32 1 0.0833 54.381 0.1515 23.94 D
B noktasından yüksekliği D 1.072m olarak bulunur.
7
SORU 2.12
Şekilde gösterilen a=3m çapındaki atmosfere açık silindirik bir tankın tabanı küresel
geometride olup, içerisinde b=8m yükseklikte su bulunmaktadır. Tabandaki eğrisel yüzey
üzerine etki eden su kuvvetinin şiddetini, yönünü ve tatbik noktasını tespit ediniz?
ÇÖZÜM
Etki eden kuvvetin şiddeti tank içerisindeki suyun ağırlığına eşittir.
FR = ρg(Vsilindir – Vyarımküre)
m π
π
kg
FR 999 3 9.807 2 (3 m) 2 (8 m) (3 m)3
m
s 4
12
FR=484766 N =485 kN
Simetri söz konusu olduğundan yatay kuvvetler dikkate alınmayabilir (çünkü kuvvetler arası
denge söz konusudur). Bu durumda net kuvvetin doğrultusu ve yönü; tank merkezinden
geçen eksende aşağıya doğrudur. Tatbik noktası ise eğrisel yüzeyin merkez noktasıdır.
SORU 2.13
Şekilde gösterilen 3m uzunluğundaki eğrisel (çeyrek daire) kapak su dolu bir rezervuara
monte edilmiştir. Kapak yarıçapı R=2m, su derinliği h=6m iken;
a) Kapak üzerine etki eden su kuvvetinin yatay ve düşey bileşenlerinin değerlerini tespit
ediniz?
b) Bileşke (net) kuvvetin, tatbik noktasını ve düşey eksen ile yaptığı açıyı bulunuz
8
ÇÖZÜM
Yatay yöndeki kuvvet 3mx2m boyutlarında düzlemsel yüzeye etki eder.
1 3
ba
I xc
y R yc
yc 12
abyc
Ayc
a2
(2 m) 2
5m
5.06 m
12 y c
12(5 m)
FR ρgAh c (999)(9.807)(2)(3)(5) 293916 N FH
yR yc
FH=FR
a=2m
6 – 5.06
b=3m
0.93 m
Düşey kuvvet, kapak üzerindeki suyun ağırlığına eşittir.
Fv=W=gV=(999 kg/m3)(9.807 m/s2) [(4 m)(2 m)+(/4)(2 m)2](3 m)
Fv=327563 N
Düşey kuvvetin merkezden uzaklığı:
π
π
2
2 4(2 m)
(4 m)(2 m) 4 (2 m) a v (4 m)(2 m)(1 m) 4 (2 m) 3π
av=0.957 m
FV
aV
Bileşke kuvvet ve açısı:
FR = (FH2 + FV2)1/2 = 440152 N
327563
θ tan 1
48.1
294000
C
FR
aH
θ
B
aV
9
SORU 2.14
Şekilde gösterilen 2m genişliğindeki kapı, bir halat vasıtasıyla ‘M’ kütlesine sahip bir
silindire bağlanmıştır. Su seviyesi 2.5 m’ye düştüğü zaman kapı açılmaktadır. Mafsal
sürtünmesini ihmal ederek silindir kütlesi ile mafsal kuvvetinin şiddetini ve yönünü bulunuz?
ÇÖZÜM
Net kuvvet
h
FR ρgh c A ρg A(2) ρgh 2
2
Kapının serbest cisim diyagramı
Silindirin serbest cisim diyagramı
T
W
FB
M mafsal 0
(saatin ters yönü pozitif)
h
FR 0
3
h
h
1
1
T FR ρgh 2 ρgh 3 (999)(9.807)(2.5)3 12757 N
12
12
12
12
4T
Fy 0 (silindir için)
T FB W 0
π
π
FB ρgV ρg D 2 (h 1 m) (999)(9.807) (1) 2 (2.5 1) 11542 N
4
4
W Mg T FB
T FB 12757 N 11542 N
M
2477.7 kg M
g
9.807 m 2 / s
Fx T FR Fmafsal 0 (kapı için)
Fmafsal FR T gh 2 12757 …………… Fmafsal=48475 N
10
SORU 2.15
Bir araba yarışçısı, 7 m/s2’lik ivme ile hızlanırken , kahve fincanını yatay olarak
yerleştirmektedir. Fincan 10 cm derinliğinde ve 6 cm çapında olup sakin halde 7 cm
derinliğinde kahve içermektedir. Buna göre ;
a) Katı cisim ivmelenmesi kabul ederek kahvenin fincandan dökülüp dökülmeyeceğini
belirleyiniz?
b) Kahvenin yoğunluğu belli ise A köşesindeki etkin basıncı bulunuz?
ÇÖZÜM
az = 0’dır buna göre θ açısı ;
tan 1
7,0
ax
tan 1
35,5
9,81
g
Fincanın sol yanındaki yükselme miktarı ;
z 3cm. tan 2,14cm
Bu yükselme, 3 cm’lik mevcut açıklıktan daha azdır. Bu nedenle ivme başlangıcında
çalkalanma olmadıkça kahve dökülmeyecektir. Durma halinde A noktasındaki etkin basınç ;
PA g ( Z yuzey Z A ) 694kPa
İvmelenme sırasında yerçekimi ivmesine ilave olarak parçacık ivmelenmesi oluşacaktır.
Toplam ivme;
G 7,0 2 9,812
1/ 2
12,05m / s 2
olarak bulunur. Eğik yüzeyden A noktasına olan normal boyunca aşağıya doğru ΔS uzaklığı ;
S (7,0cm 2,14cm).(cos 35,5) 7,44cm
A noktasındaki basınç ;
PA gS 1010.12,05.0,0744 906 Pa
Bu değer durgun haldeki basınç değerinden % 31 daha büyüktür.
11
SORU 2.16
Bir önceki örnekteki kahve fincanı bir pikap üzerine yerleştirilerek blok halinde dönme
durumu oluşuncaya kadar simetri ekseni etrafında döndürülüyor.
a) Kahvenin kabın tam üst kenarına ulaşmasına neden olacak açısal hızı bulunuz?
b) Bu durumda kabın A noktasındaki etkin basıncı bulunuz?
ÇÖZÜM
Fincanda 7 cm kahve vardır. Kenara kadar olan 3 cm’lik mesafe konu anlatımındaki h/2
uzunluğuna eşit olmalıdır. Buna göre ;
h
2R2
0,03m
2 1308 36,2 r / s 345d / dak
2
4g
Basıncı hesaplamak için r ve z koordinatlarının başlangıcını serbest yüzey alçalmasının
olduğu B noktasına koymak uygundur. Etkin basınç burada 0’dır. A noktası ( r , z ) = ( 3 cm ,
-4 cm )’dedir. Böylece PA ;
PA 0 1010kg / m 3 9,81m / s 2 . 0,04m
1
1010kg / m 3 .0,03m 2 1308r 2 / s 2
2
PA 990 Pa
Bu basınç değeri durgun haldeki basınç olan 694 Pa’dan % 43 daha büyüktür.
12