AÇILAR Tanım : Ortak uçlu iki ışının oluşturduğu şekildir. Yan

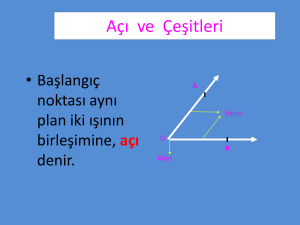
AÇILAR
Tanım : Ortak uçlu iki ışının oluşturduğu şekildir.
Yandaki sarı boyalı bölge ortak uçlu iki ışının oluşturduğu
açıdır. Açı modelimizde çizdiğimiz dairesel çizgiler üzerine
açının ölçüsü yazılır ve yan tarafta gördüğünüz her dairesel
çizginin açı ölçüsü eşittir. Açı ölçüsünün değerini dairesel
çizgiler belirlemez. Işınların başlangıç noktası belirler.
Yan taraftaki açının değerini değiştirmek için ışınların arasındaki mesafe miktarını
değiştirmemiz yeterlidir. Aksi halde dairesel çizgilerden büyük olanı büyük açı, küçük
olanı küçük açı denmez. İki ışının arasındaki dairesel çizgiler her zaman eşit açı
ölçülerini temsil eder. Zaten iki ışın arasına normalde sadece bir tane dairesel çizgi çizilir
ve açının değeri üzerine yazılır. Burada dairesel çizginin aslında temsili bir işaret
olduğunu belirtmek için 3 tane dairesel çizgi çizdim.
AÇILARDA BÖLGELER :
İç Bölge : İki ışın arasında kalan bölge açılarda iç bölgedir.
ÖR :
Yandaki açı modelinde ;
K ve M noktaları üçgenin iç
bölgesindedir.
.K
İç bölge
.M
Dış Bölge : İki ışının arasında olmayan bölge dış bölgedir.
ÖR :
Yandaki açı modelinde ;
A,B ve C noktaları üçgenin
dış bölgesindedir.
.A
Dış bölge
İç bölge
Dış bölge
.B
.C
NOT : Işınların üzerinde olan noktalar açının üzerindeki noktalardır. İç veya dış bölgede
gösterilmez.
Yandaki açı modelinde ; M noktası açının üzerindedir. Bu
ÖR :
arada sakın M harfi açının iç bölgesinde duruyormuş gibi
M
olabilir ama M harfinin yerini belirleyen noktasının
bulunduğu yerdir. Noktası nerede ise M harfi de oradadır.
.
AÇILARIN İSİMLENDİRİLMESİ : Açılar isimlendirilirken ışınların başlangıç noktası ve ışınların her
birinin üzerinde belirtilen noktalar yardımıyla olur.
B
A
.
.
.C
Yandaki ışının ismi köşe ortaya gelecek şekilde diğer iki
noktanın arasına yazılarak bulunur. Yazım işleminin üstüne
açı sembolü mutlaka yerleştirilir.
̂ 𝑪 şeklinde ya da 𝑪𝑨
̂ 𝑩 şeklinde gösterilir. Başlangıç noktası ortada olmak şartıyla
Açının ismi 𝑩𝑨
sağa yada sola gelecek harfin sıralaması önemli değildir.
Ayrıca başlangıç noktasında sadece bir açı var ise ; sadece başlangıç noktasının üzerine açı
̂ şeklinde de isimlendirilebilir. Yalnız bu
işaretini koyarak da isimlendirme yapabiliriz. Yani 𝑨
gösterim çok sık kullanılmaz. Genelde ilk gösterdiğim isimlendirme kullanılır.
Yine bazı gösterimlerde açının üzerine konulan işaret öne de konulabilir. Yani < 𝐵𝐴𝐶 ya da <
𝐶𝐴𝐵 şeklinde isimlendirilebilir. Aynı şekilde < 𝐴 şeklinde de isimlendirilebilir.
Farkındaysanız yukarıda bir açı için çok fazla isimlendirme kullandım. Ama ilk verdiğim
isimlendirme en yaygın olan isimlendirmedir.
Yanda verilen şekilde 3 adet açı vardır. Şimdi her birinin
isimlerini ve bulundakları yeri belirleyelim.
.D
̂C
Üstte verilen açının ismi B𝑨
şeklinde belirtilir.
̂C
Üstte verilen açının ismi D𝑨
şeklinde belirtilir.
̂D
Üstte verilen açının ismi B𝑨
şeklinde belirtilir.
NOT : Yukarıdaki açıların başlangıç noktası A noktası olduğu için açılar isimlendirilir iken A
noktası her seferinde ortaya yazıldı.
̂ şeklinde de isimlendirilebilir demiştim. Ama
Ayrıca açıların isimlendirilmesi kısmında sadece 𝑨
bu durum burada geçerli değil çünkü başlangıç noktasında birden fazla açı oluşabiliyor. Sadece A
açısı yazarsak hangi açıdan bahsettiğimiz belli olmaz. Sadece A açısı yazabilmemiz için başlangıç
noktasında tek bir açı olmalı. Yukarıda 3 adet açı oluştu.
Açıları Ölçme : Açı ölçümü iletki(açı ölçer) ile yapılır. İletki ile açı ölçümünün aşamaları aşağıdaki
gibidir;
 İletkinin düz kısmı ışınlardan birinin tam üzerine gelecek şekilde çakıştırılır.
 Işınların başlangıç noktası ile iletkinin merkezi üst üste getirilir.
 İletkinin düz kısmı ile çakıştırılmayan diğer ışının iletkinin üzerinde gösterdiği değer o açının
değeridir.
Aşağıda 𝟒𝟕𝒐 ′𝒍𝒊𝒌 bir açının çizimini vereceğim.
İletkinin düz kısmı ile
çakıştırılmayan diğer ışının
iletki üzerinde gösterilen
değeri 47 derece olduğu için
bu açının ölçüsü 47 derece
olarak bulundu.
İletkinin merkezi ile
ışınların başlangıç
noktaları çakıştırıldı.
Işın ile iletkinin düz
kısmı çakıştırıldı.
Sonuç olarak yukarıdaki ışının açısal değeri 47 derece olarak bulundu. 47 dereceyi açının ismini
kullanarak göstermek için; Açının adı parantez içinde yazılır ve parantezin önüne küçük ‘s’
konularak eşittir 47 derece olarak gösterilir. Yani ;
̂ B)= 𝟒𝟕𝒐 şeklinde
s(C𝑨
gösterilir.
Sizde evde ratgele açı ölçümleri yapınız. Ölçüm yaparken iletki kullanmayı unutmayınız  .
NOT : Gönye de bir açı ölçme aletidir yalnız gönye özellikle dik açıları ölçmeye yarayan dik üçgen
biçiminde bir alettir.
.𝑮
.
.𝑹
𝑬
.𝑲
𝒐
𝟓𝟓
.𝑭
𝑷.
̂ 𝑬) = 𝟓𝟓𝒐
𝒔(𝑮𝑭
𝟏𝟏𝟎𝒐
.𝑺
̂ 𝑺) = 𝟏𝟏𝟎𝒐
𝒔(𝑹𝑷
𝑳.
𝟗𝟎𝒐
.𝑴
𝒔(𝑲𝑳̂𝑴) = 𝟗𝟎𝒐
NOT : Yukarıdaki ışınların başlangıç noktalarında sadece bir açı oluşabildiği için açı ölçümlerini
sadece başlangıç noktasını kullanarak da gösterebilirdik.
̂ ) = 𝟓𝟓𝒐 şeklinde de yazabilirdik.
1. gösterdiğim açı için ; 𝒔(𝑭
̂ ) = 𝟏𝟏𝟎𝒐 şeklinde de yazabilirdik.
2. gösterdiğim açı için ; 𝒔(𝑷
3. gösterdiğim açı için ; 𝒔(𝑳̂) = 𝟗𝟎𝒐 şeklinde de yazabilirdik.
Aşağıdaki açı modellerini inceleyilim ;
.
𝑪
𝑫
𝟗𝟓𝒐
.
𝑨
𝟑𝟑𝒐
Yandaki açı modellerinde ;
.
𝑩
.
̂ 𝑫) = 𝟗𝟓𝒐
𝒔(𝑪𝑨
̂ 𝑫) = 𝟑𝟑𝒐
𝒔(𝑩𝑨
̂ 𝑩) = 𝟗𝟓𝒐 + 𝟑𝟑𝒐 = 𝟏𝟐𝟖𝒐
𝒔(𝑪𝑨
Komşu Açılar : Köşeleri ve birer ışınları ortak olan açılar komşu açılardır.
Yandaki açı modellerinde ;
̂ 𝑫 𝒗𝒆 𝑩𝑨
̂ 𝑫 𝒂ç𝚤𝒍𝒂𝒓𝚤 𝒌𝒐𝒎ş𝒖 𝒂ç𝚤𝒍𝒂𝒓𝒅𝚤𝒓.
𝑪𝑨
Ters Açılar : İki doğrunun kesişmesi sonucunda ters yönde oluşan eş açılara ters açılar denir.
Yandaki açı modellerinde ;
.𝑩
𝑪
.
𝑨
𝑫.
.𝑬
̂ 𝑪 𝒊𝒍𝒆 𝑬𝑨
̂ 𝑫 𝒂ç𝚤𝒍𝒂𝒓𝚤 𝒕𝒆𝒓𝒔 𝒂ç𝚤𝒍𝒂𝒓𝒅𝚤𝒓.
𝑩𝑨
̂ 𝑫 𝒊𝒍𝒆 𝑬𝑨
̂ 𝑪 𝒂ç𝚤𝒍𝒂𝒓𝚤 𝒕𝒆𝒓𝒔 𝒂ç𝚤𝒍𝒂𝒓𝒅𝚤𝒓.
𝑩𝑨
NOT : Ters açıların ölçüleri birbirine eşittir.
TÜMLER VE BÜTÜNLER AÇILAR :
Tümler Açılar : Ölçüleri toplamı 90 derece olan iki açıya tümler açı denir.
𝑲
𝑪.
.
.𝑹
𝟑𝟐𝒐
𝑷
𝑳.
Yandaki açıların toplamı 90 derece olduğu
için;
𝟓𝟖𝒐
.𝑻
.
̂ R açısı ile K𝑳̂T açısı tümler açılardır.
P𝑪
̂ R) + s(K𝑳̂T) = 𝟑𝟐𝒐 + 𝟓𝟖𝒐 = 𝟗𝟎𝒐
s(P𝑪
Komşu Tümler Açılar : Dik açı oluşturan komşu açılara komşu tümler açılar denir.
𝑨.
̂ D ile D𝑩
̂ C açılarının
Yandaki A𝑩
toplamı 90 derecedir. Bu iki açı aynı
zamanda komşu açılar oldukları için komşu
tümler açılardır.
𝑫.
𝟕𝟎𝒐
𝟐𝟎𝒐
𝑩.
.
𝑪
̂ D) + s(D𝑩
̂ C) = 𝟕𝟎𝒐 + 𝟐𝟎𝒐 = 𝟗𝟎𝒐
s(A𝑩
Bütünler Açılar : Ölçüleri toplamı 180 derece olan iki açıya bütünler açı denir.
̂ B ile K𝑳̂M açılarının
Yandaki G𝒁
toplamı 180 derecedir. Bu iki açıya bu
yüzden bütünler açılar denir.
𝑲.
.
𝑮
.
𝟏𝟏𝟎𝒐
𝑩
.
𝒁
.
𝑳
𝟕𝟎𝒐
.
𝑴
̂ B) + s(K𝑳̂M) = 𝟏𝟏𝟎𝒐 + 𝟕𝟎𝒐 = 𝟏𝟖𝟎𝒐
s(G𝒁
Komşu Bütünler Açılar : Doğrusal bir çift oluşturan komşu açılara komşu bütünler açılar denir.
𝑷
̂ T ile T𝑹
̂ S açılarının toplamı 180
Yandaki P𝑹
derecedir. Bu iki açı aynı zamanda komşu açılar
oldukları için komşu bütünler açılardır.
.
𝑹.
𝟏𝟑𝟎𝒐
𝟓𝟎𝒐
𝑺
.
𝑻
.
̂ T) + s(T𝑹
̂ S) = 𝟏𝟑𝟎𝒐 + 𝟓𝟎𝒐 = 𝟏𝟖𝟎𝒐
s(P𝑹
̂ S)= 𝟏𝟖𝟎𝒐 olduğuna dikkat ediniz. 180 derecelik
s(P𝑹
açılara doğrusal açılar dendiğini unutmayalım.
Not : Tümler açılar ve bütünler açıları karıştıran öğrenciler için basit bir hatırlatma yöntemi
vereyim. Tümlerin harf sayısı az olduğu için 90 dereceyi temsil eder, bütünlerin harf sayısı
fazla olduğu için 180 dereceyi temsil eder.
ÇÖZÜMLÜ ÖRNEK SORULAR
1. [KM ve [KC ışınlarının oluşturduğu açı aşağıdakilerden hangisidir ?
̂M
B) K𝑪
̂C
A) K𝑴
̂C
C) M𝑲
̂K
D) C𝑴
ÇÖZÜM :
M.
K.
C
.
Açı isimlendirmelerinde iki ışının kesişim noktası ortaya
gelecek şekilde yazılır. Işınlarının kesişim noktasının
sağına ve soluna gelecek olan harf ise farketmez. Öyleyse
̂ C ya da C𝑲
̂ M’ dir. Doğru cevap C
açımızın ismi M𝑲
şıkkıdır.
Ayrıca K noktasının etrafında başka bir açı oluşmadığına
̂ açısı olarak da
göre bu açının ismini sadece 𝑲
isimlendirebilirdik.
2.
T
A .
Yanda verilen TAK açısında
aşağıdakilerden hangisi mevcut değildir?
.
.
A) [AT]
B) [AK]
C) [AT
D) [KA
K
ÇÖZÜM : Yukarıdaki açı modelinde şıklarda verilenlerden AT doğru parçası vardır, AK doğru
parçası vardır ve AT ışını vardır. D şıkkındaki [KA ışını ise yoktur. Çünkü ışın modellerinde yazılım
başlangıç noktasına göre yapılır. D şıkkının doğru olabilmesi için [AK ışını şeklinde yazılmalıydı ki
AK ışını açı modelimizde mevcut olurdu. D şıkkı doğru cevaptır.
3.
S.
L
.
. K
M.
D
.
.
E
Yanda verilen LMD açısına göre aşağıdakilerden hangisi
yanlıştır?
A) E noktası LMD açısının elemanıdır.
B) S noktası LMD açısının dış bölgesindedir.
C) K noktası LMD açısının dış bölgesindedir.
D) D noktası LME açısının elemanıdır.
ÇÖZÜM : Verilen açı modelinde E noktası LMD açısının elemanıdır. Buradaki elemanıdır cümlesi
noktanın tam açı üzerinde olduğunu belirtiyor. S noktası LMD açısının dış bölgesindedir. K noktası
ise LMD açısının iç bölgesindedir. İşaretlememiz gereken şık C şıkkıdır. D şıkkında bir çeldirici var.
Soruda LMD açısı olark yazdık ama D şıkkında LME açısı olarak isimlendirilmiş. LMD açısı ile LME
açısı aynı açıyı ifade eder. Çünkü D noktası ve E noktası aynı ışın üzerindedir. Önemli olan
başlangıç noktası olan M noktasını ortaya almak ve diğer iki ışından birer noktayı sağına ve soluna
yazmak. Dolayısıyla LME ışınında herhangi bir yazım hatası yoktur ve D noktası da LME açısının
tam üzerinde olduğu için D noktası LME açısının elemanıdır.
4.
Yanda verilen şekle göre TZV açısı
ile YV doğrusunun kesişimi
aşağıdakilerden hangisidir?
.V
.T
Y.
.Z
A) VY
B) {V,Y}
C) [ZV
D) [ZY
ÇÖZÜM : Bu tarz soruların çözümü için kesişimi istenen ögelerin her biri farklı renklerde boyanır.
Boyama sonucunda renklerin kesiştiği yer bizim cevabımız olacaktır. Aşağıdaki çözüm şeklini
inceleyiniz.
̂ V açısı mavi renk ile boyandı.
T𝒁
YV doğrusu kırmızı renk ile boyandı.
Her ikisinin kesişimi Y ve V noktaları
sarı renk ile gösterildi.
Doğru cevap B şıkkı.
NOT : Bu tarz kesişim sorularında doğru cevap her zaman nokta çıkacak diye bir durum yok.
Kesişim ışın da olabilir, doğru parçası da olabilir, doğru da olabilir. Burada ortak eleman Y ve V
noktaları oldu.
Bu sorunun cevabını matematiksel olarak şu şekilde ifade edebiliriz;
̂ 𝒀 ∩ 𝒀𝑽 = {𝑽, 𝒀}
𝑻𝒁
5.
𝟐𝟎𝒐
K
.
.
O.
.L
Yanda verilen açıölçerde iki farklı ışının
oluşturduğu açı 20 derece olarak ölçülmüştür.
Buna göre aşağıdakilerden hangisi yanlıştır?
A) LOK açısını 70 derece arttırır isek dik açı oluşur.
B) LOK açısını 80 derece arttırır isek geniş açı oluşur.
C) LOK açısı 160 derece arttırır isek doğru açı olur.
D) LOK açısını 20 derece düşürürsek dar açı oluşur.
ÇÖZÜM :
A) 20 + 70= 90 derece dik açı olur (doğru)
B)20 + 80= 100 derece geniş açı olur (doğru)
C) 20 + 160= 180 derece doğru açı olur (doğru)
D) 20 −20= 0 derece dar açı olmaz. (yanlış)
6.
D
.
C
.
K
Aşağıdakilerden hangisi yanlıştır?
.
̂ 𝑪 ile 𝑲𝑴
̂ 𝑪 komşu açılardır.
A) 𝑫𝑴
̂ 𝑪 ile 𝑲𝑴
̂ 𝑻 komşu açılardır.
B) 𝑲𝑴
̂ 𝑲 ile 𝑲𝑴
̂ 𝑻 komşu açılardır.
C) 𝑫𝑴
̂ 𝑪 ile 𝑲𝑴
̂ 𝑻 komşu açılardır.
D) 𝑫𝑴
T
.
.
M
ÇÖZÜM : İki açının komşu açı olabilmesi için aralarında başka bir açı olmaması lazım. d şıkkında
̂ C ile K𝑴
̂ T arasında K𝑴
̂ C açısı var.Dolayısıyla DMC açısı ile KMT açısı komşu açı olamaz.
D𝑴
7.
.K
.L
𝟔𝟎𝒐
T
.
.
𝟒𝟎𝒐
A
B
Yandaki şekle göre aşağıda verilen açı
ölçülerinden hangisi yanlıştır?
.
E
.
̂ B)= 𝟒𝟎𝒐
A) s(T𝑨
̂ D)= 𝟏𝟎𝟎𝒐
B) s(K𝑨
̂ K)=𝟖𝟎𝒐
C) s(L𝑨
̂ B)=𝟏𝟐𝟎𝒐
D) s(L𝑨
.D
ÇÖZÜM : Her bir şıkkı ayrı ayrı inceleyelim ;
A şıkkı ;
̂ B) açısının ölçüsünü istemiş.
Bizden s(T𝑨
TAB açısı yandaki şekilde boyalı olarak
belirtilen KAE açısı ile ters açıdır. Ters
açılar birbirine eşit olduğu için;
𝟒𝟎𝒐
̂ E) = s(T𝑨
̂ B) = 𝟒𝟎𝒐
s(K𝑨
A şıkkı doğrudur.
B şıkkı ;
𝟔𝟎𝒐
𝟏𝟎𝟎𝒐
̂ D) açısının ölçüsünü istemiş. KAD açısı yandaki
Bizden s(K𝑨
şekilde sarı renk ile gösterilmiştir. Sarı bölge KAE açısı ile EAD
̂ E)= 𝟒𝟎𝒐 olduğu
açısı olmak üzere iki parçadan oluşuyor. s(K𝑨
belli. Bize pembe ile boyadığım bölge lazım ki o EAD açısı 60
derecelik ölçüye sahip olan LAT açısı ile ters açıdır. Bu iki ters
açıyı özellikle pembe ile boyadım. Ters açıların eşit olduğunu
̂ D)= s(K𝑨
̂ E) + s(E𝑨
̂ D)= 𝟒𝟎𝒐 + 𝟔𝟎𝒐 =𝟏𝟎𝟎𝒐
bildiğimize göre ; s(K𝑨
B şıkkı doğrudur.
C şıkkı ;
Yandaki şekilde yeşil ile boyadığım açılar doğrusal bir açı
oluşturuyor. Doğrusal açılar bir doğrunun tamamını
içeren açılardır. Doğrusal açılar toplamı her zaman 180
derecedir.
𝟖𝟎𝒐
̂ 𝑳)+ s(L𝑨
̂ K) + s(K𝑨
̂ E)= 𝟏𝟖𝟎𝒐 olmak zorunda. TAL
s(T𝑨
açısı ile KAE açısı toplamı 100 derece olduğuna göre LAK
açısı 80 derece olmalı ki toplamda bir doğrusal açı versin.
C şıkkı doğrudur.
D şıkkı ;
Yandaki şekilde pembe ile boyadığım açılar ters açılardır.
̂ B açısının
Ters açılar da birbirine eşit olduğu için T𝑨
ölçüsü 40 derece olmak zorunda.
𝟏𝟎𝟎𝒐
̂ 𝑩)= s(L𝑨
̂ T) + s(T𝑨
̂ E) olduğuna göre ;
s(L𝑨
𝟒𝟎𝒐
̂ 𝑩)= 𝟔𝟎𝒐 + 𝟒𝟎𝒐 = 𝟏𝟎𝟎𝒐 olur.
s(L𝑨
D şıkkı yanlıştır.
8.
Yandaki şekilde iki komşu tümler açı verilmiştir.
Verilmeyen açı aşağıdakilerden hangisidir?
.
A) 𝟐𝟓𝒐
?
B) 𝟒𝟓𝒐
C) 𝟔𝟓𝒐
D) 𝟕𝟓𝒐
𝟐𝟓𝒐
ÇÖZÜM : İki tümler açının toplamı 90 derecedir. Biri 25 olduğuna göre diğeri 90-25= 𝟔𝟓𝒐 olmalı.