cebirsel ifadeler - Z

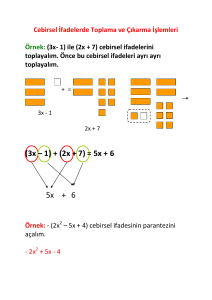
CEBİRSEL İFADELER
3x + 2y - 6 cebirsel ifadesinde
3x + 2y -6
1.terim
2.terim 3.terim
3x ifadesinde 3 katsayıdır.
3x + 2 y -6 ifadesinde 3 , 2 , - 6 katsayıdır.
2) Aşağıdaki cebirsel ifadelerde toplama ve
çıkarma işlemlerini yapınız.
a) x  x 
b) x  x + x 
c) x  x  x  x 
d) 2x  x 
yanında harf bulunmayan tamsayılara
e) x  4x 
aynı zamanda sabit terim denir.
f) x  3x  x 
1) Aşağıdaki cebirsel ifadelerde terim sayısını ,
sabit terimi , katsayılarını ve bilinmeyen
sayısını belirleyiniz.
a) 5x  3y  5 cebirsel ifadesinde
Terim sayısı:
Katsayıları:
Sabit terimi:
bilinmeyen sayısı:
b)
4x  8y  1 cebirsel ifadesinde
Terim sayısı:
Katsayıları:
Sabit terimi:
Bilinmeyen sayısı:
c)
x + 9y +2 cebirsel ifadesinde
Terim sayısı:
Katsayıları:
Sabit terimi:
Bilinmeyen sayısı:
d) x + y  3 cebirsel ifadesinde
Terim sayısı:
b) 4x  5x + x 
c) 5x  3x  2x  6x 
d) 2x  7x 
e) 9x  4x 
f) 6x  3x  x 
a) x  x 
b) 5x  x 
c) 4x  x 
d) 7x  6x 
e) 5x  4x 
f) 6x  3x 
a) x  4x 
b) x  7x 
c) x  6x 
d) 3x  6x 
e) 5x  9x 
f) 2x  3x 
Katsayıları:
Sabit terimi:
a)  x  4x 
Bilinmeyen sayısı:
c)  3x  7x 
e) -3x + y +6 cebirsel ifadesinde
f)
a) 3x  2x 
b)  2x  6x 
d)  4x  x 
Terim sayısı:
Katsayıları:
Sabit terimi:
e)  5x  x 
Bilinmeyen sayısı:
a) x + 4x  x 
-x  y  7 cebirsel ifadesinde
Terim sayısı:
Katsayıları:
Sabit terimi:
Bilinmeyen sayısı:
f)  x  x 
b) x + 5x  2x 
c) 2x + 3x  7x 
d) x  4x  4x 
e) x  5x  2x 
f) 9x  3x  5x 
CEBİRSEL İFADELER
a) x + 4x  x  x 
a) 3  3x  5  
b) x + 5x  x  5x 
b) 4  5x  2  
c) 7x + 4x  2x  3x 
d) 2x  4x  3x + 6x 
e) 3x  2x +5x  8x 
f)  5x + 6x +2x  7x 
a) x + 4x + 5 + 3 
c) 2  2x  3 
d) 5  2x  5  
e) 2  1  3x  
f) 7  2  4x  
b) x + 5x  7  2 
a)  3  4x + 5  
c) 7x + 4 + 2x  3 
b)  4  5x + 4  
d) 2x  8  3x + 6 
c)  2  x + 7  
e) 3  2x +5x  9 
f)  4x + 6 + 5x  7 
 2x  4    x  6  
b)  3x  1   x  5  
c)  5x  4    2x  7  
d)  x  4    4x  1 
e)  2  4x    3  6x  
f)  3  5x    7  8x  
a)
d)  5  x  5  
e)  2 1  3x  
f)  7  2  4x  
a)
 2x  3   3x  5  
b)
 5x  4    x  1 
c)
 6x  2    7x  7  
d)
 x  5   3x  5  
e)
 3x  6    6x  4  
f)
 2x  3   5x  1 
3) Aşağıdaki dağılma işlemlerini yapınız.
a)   2x  4  
b)   3x  6  
c)   x  1 
d)   x + 4  
e)   3 +7x  
f)   2  4x  
a) 2  2x  3  3  3x  5  
a)   5x  2  
b) 3  5x  4   2  x  1 
b)   2x  1 
c)   5x  3 
d)    x  4  
e)   3  x  
f)   2  6x  
c) 2  6x  2   3  7x  7  
d) 4  x  5   2  3x  5  
e) 3  3x  6   4  6x  4  
f)
 2x  3  3  5x  1 
CEBİRSEL İFADELER
4) Aşağıdaki cebirsel ifadelerde x’in değerini
cebirsel ifadede yerine yazınız.
x  2 için
5) Aşağıdaki geometrik şekillerin kenar
uzunlukları cebirsel olarak verilmiştir. Buna
göre çevrelerini cebirsel olarak belirtiniz.
a)
a) x+3
b) 5 + x
c) x + 6
d) 2x
e) 3x
f) 4x +2
b)
x  2 için
a) x  3
b) 5  x
c) x  6
d) 2x  5
e) 3x  8
c)
f) 4x  2
x  2 için
a) x + 5
b) 2 + x
c) x + 7
d) 3x + 2
d)
e) 4x + 8
f) 5x + 3
x  3 için
a) x  4
b) 5  3x
c) x  6
e)
d) 3  4x
e) 2x  5
f) 4x  7
x  4 için
a)  x  4    x  3
b)  3  2x    5  3x 
c)  x  3  2  x  6 
d) x  3  4x 
e) 2x  x  5 
f)  4x  7  x  2 
f)
CEBİRSEL İFADELER
6) Aşağıdaki şekillerin çevre uzunluklarını
bulunuz.
a)
7) Aşağıdaki sayı örüntülerinin genel kurallarını
bulunuz.
a) 2 , 4 ,6 ,8, 10, ....
b) 1 , 3, 5 ,6, 7, ....
c) 2, 5, 8,11,14, ....
d) 2, 6, 10, 14, 18, ....
e) 1 , 5 , 9 , 13 , 17....
f) 1, 4 , 7, 10 ,13 , ....
b)
a) 6 , 10 ,14 , 18 ,...
b) 15 ,17 ,19 , 21 ,....
c) 45, 50 ,55, 60, 65 ...
d) 23,30 ,37, 44,...
c)
e) 33 , 38 ,43, 48,...
f) 29 ,32, 35, 38,....
8) Aşağıda genel kuralı verilen sayı örüntülerinin
ilk beş terimini bulunuz.
a) 2n
d)
b) 3n
c) 2n+1
d) 2n  1
e) 3n+2
f) 4n  1
g) 3n+5
e)
h) 6n  3
9) Aşağıda genel kuralı verilen sayı örüntülerinin
artış miktarlarını bulunuz.
a) 2n
b) 4n
c) 5n+1
d) 3n  1
f)
e) n+2
10) Aşağıda genel kuralı verilen sayı örüntülerinin
24. Sıradaki sayının kaç olduğunu bulunuz.
a) 3n-2
b) 4n+1
c) 5n  3
d) 2n+14
e) 5n+2