ELEKTRİKSEL POTANSİYEL

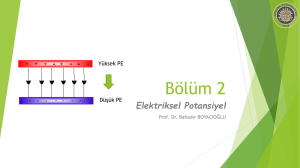
ELEKTRİKSEL POTANSİYEL
Elektriksel Potansiyel Enerji
Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1
dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin
korunumu kavramları ile ilgili üç ana noktayı yeniden gözden
geçirelim.
1. Eğer bir 𝐹 kuvveti 𝑎 noktasından 𝑏 noktasına giden bir parçacık
üzerine etki ediyorsa, bu kuvvetin yaptığı iş bir çizgi integrali ile
verilir.
Burada 𝑑𝒍, parçacığın izlediği yol üzerindeki sonsuz küçük bir
yerdeğiştirme, ∅ ise yolun her noktasında 𝑭 ile 𝑑𝒍 arasındaki
açıdır.
2. Eğer bir 𝑭 kuvveti korunumlu ise (Yani bir kuvvetin bir işi
yapması izlediği yoldan bağımsız ise böyle kuvvetlere korunumlu
kuvvet denir), 𝑭′ in yaptığı iş her zaman 𝑈 ile gösterilen bir
potansiyel enerji olarak ifade edilir. Eğer bir parçacık potansiyel
enerjinin 𝑈𝑎
olduğu noktadan 𝑈𝑏
olduğu noktaya hareket
ettiriliyorsa potansiyel enerjideki değişim ∆𝑈 = 𝑈𝑏 − 𝑈𝑎 (Son
potansiyel-İlk Potansiyel) olur ve bu kuvvetin yaptığı iş;
Kuvvetin yaptığı iş (𝑊𝑎
𝑏)
pozitif değerler alıyorsa, 𝑈𝑎 , 𝑈𝑏 ′ den
büyüktür ve potansiyel enerjideki değişim (∆𝑈) ise negatif değer alır
ve böylece potansiyel enerji azalır.
Örneğin bir beysbol topunun yerin kütle
çekimi
etkisiyle
noktasından
daha
yüksekteki
(a)
aşağıdaki
(b)
noktasına düşmesi durumunda kütle
çekim kuvveti pozitif iş yaparken kütle
çekim enerjisi azalmaktadır.
Son olarak iş-enerji teoremine göre, herhangi bir yer değiştirme
sırasında oluşan kinetik enerjideki değişim (∆𝐾 = 𝐾𝑏 − 𝐾𝑎 ), parçacık
üzerindeki yapılan toplam işe eşittir. Bu tanım aşağıdaki eşitliği
sağlamaktadır.
𝐾𝑏 − 𝐾𝑎 = −(𝑈𝑏 − 𝑈𝑎 )
Bunun anlamı toplam mekanik enerjinin (kinetik ve potansiyel
toplamı) korunmuş olmasıdır.
Bu temel kavramların ardından sabit bir elektrik alanında
elektriksel potansiyel enerji kavramını incelemeye çalışalım.
Sabit Bir Elektrik Alanında Elektriksel Potansiyel Enerji
Aşağıdaki şekilde gösterildiği gibi iki yüklü paralel metal levhanın
aşağıya doğru büyüklüğü 𝐸 olan düzgün bir elektrik alanı oluşturduğu
düşünelim.
Kütlesi 𝑚 olan bir beysbol topuna etki eden kütle çekim kuvvetinin
sadece y ekseni bileşeni olup değeri 𝐹𝑦 = −𝑚𝑔 dir. Aynı zamanda
kütle çekim kuvveti için potansiyel enerji ise 𝑈 = 𝑚𝑔𝑦 ifadesiyle
tanımlanmaktadır.
Benzer şekilde iki levha arasındaki bir deneme yüküne etki eden
elektriksel kuvvet -y ekseni doğrultusunda olup değeri 𝐹𝑦 = −𝑞0 𝐸 ile
ifade edilmekte olup bu kuvvet için potansiyel enerji ifadesi aşağıdaki
gibi tanımlanmaktadır.
Deneme yükü 𝑦𝑎 yüksekliğinden 𝑦𝑏 yüksekliğine giderse, elektrik
alanının yük üzerinde yaptığı iş aşağıdaki gibi yazılmaktadır.
Bu durumda eğer 𝑦𝑎 , 𝑦𝑏 ’den büyükse elektrik alanı pozitif iş
yapmakta olup potansiyel enerji azalmaktadır. Tam tersine 𝑦𝑎 , 𝑦𝑏 ’den
küçükse elektrik alanı negatif iş yaparken potansiyel enerji
artmaktadır. (Bir beysbol topu için aynı durumlar söz konusudur).
Dolayısıyla mekanikte olduğu gibi (Fizik-1) potansiyel enerji için
aşağıdaki durumlar.
1. Sonsuz küçük bir 𝑑𝒔 yer değiştirmesi için, bir deneme yükü
üzerine elektrik alan tarafından yapılan iş, 𝑭 ∙ 𝑑𝒔 = 𝑞0 𝑬 ∙ 𝑑𝒔 ile
verilir. Elektrik alanı tarafından bu miktarda iş yapılırken yük
ve elektrik alanından oluşan bir sistemin potansiyel enerjisi
𝑑𝑈 = −𝑞0 𝑬 ∙ 𝑑𝒔 kadar azalır.
2. Bir deneme yükünün A ve B noktaları arasında sonlu bir yer
değiştirmesi yapması durumda, sistemin ∆𝑈 = 𝑈𝐵 − 𝑈𝐴 potansiyel
enerji değişimi,
İntegrali ile hesaplanmaktadır.
İntegral 𝑞0 deneme yükünün A’ dan B’ ye gittiği yol boyunca alınır
ve adına yol integrali veya çizgi integrali denir. Bu iki terim eş
anlamlı olup 𝑞0 𝑬 kuvveti korunumlu olduğundan, bu çizgisel
integral A ve B noktaları arasında alınan yola bağlı değildir.
3. Birim yük başına 𝑈/𝑞0 potansiyel enerjisi niceliğine elektriksel
potansiyel 𝑉 (veya kısaca potansiyel) denir. O halde elektrik alanın
her hangi bir noktasındaki elektriksel potansiyel 𝑉 =
büyüklük skaler bir niceliktir.
𝑈
𝑞0
dır ve bu
4. Bir elektrik alan içinde A ve B gibi herhangi iki nokta arasındaki
∆𝑉 = 𝑉𝐵 − 𝑉𝐴 potansiyel farkı, sistemin potansiyel enerjisindeki
değişimin, 𝑞0 deneme yüküne oranı olarak tanımlanır:
Bu durumda ∆𝑉 =
∆𝑈
𝑞0
=−
𝐵
𝑬
𝐴
∙ 𝑑𝒔
eşitliğindeki A noktasını
sonsuzdaki bir nokta olarak alırsak, herhangi bir P noktasındaki
elektriksel potansiyel;
NOT ALINIZ
𝑈; Potansiyel enerji
∆𝑈; İki nokta arasındaki potansiyel enerji değişimi (∆𝑈 = 𝑈𝐵 − 𝑈𝐴 )
𝑉;Herhangi bir noktadaki potansiyel
∆𝑉; İki nokta arasındaki potansiyel fark (∆𝑉 = 𝑉𝐵 − 𝑉𝐴 )
Düzgün Bir Elektrik Alandaki Potansiyel Fark
Düzgün bir elektrik alanının negatif 𝑦 ekseni boyunca yöneldiği ve
aralarındaki uzaklığın 𝑑 olduğu A ve B gibi iki nokta arasındaki
potansiyel farkı belirlemeye çalışalım.
Şekildeki 𝑑 uzaklığı elektrik alan çizgilerine paralel olduğundan
(cos 𝜃 = cos 0° = 1) B noktası ile A noktası arasındaki
potansiyel farkı;
𝐸 sabit olduğundan potansiyel fark ifadesi aşağıdaki gibi elde edilir.
Elde edilen bu ifadedeki eksi işareti, B noktasının A noktasından daha
düşük potansiyelde olmasından kaynaklanır, yani 𝑉𝐵 < 𝑉𝐴 dır.
Şimdi ise 𝑞0 deneme yükünün A dan B’ ye gittiğinde potansiyel
enerjisindeki değişimi belirlemeye çalışalım.
ifadesi kullanılarak potansiyel enerjideki değişim;
Elde edilen bu sonuca göre 𝑞0 pozitifse, ∆𝑈 negatif olmaktadır.
Dolayısıyla bir pozitif yük elektrik alan doğrultusunda hareket ederse,
elektriksel potansiyel enerjini kaybetmektedir. Bir başka ifadeyle bir
pozitif deneme yükü, elektrik alan içinde durgun halden serbest
bırakılırsa, elektrik alan doğrultusunda 𝑞0 𝑬 elektriksel kuvvetin etkisi
altında kalır ve böylece yük kinetik enerji kazanarak aşağı doğru
hızlanırken kazandığı kinetik enerjiye eşit miktarda potansiyel enerji
kaybeder.
Eğer 𝑞0 negatifse, ∆𝑈 pozitif olur ve olay ters yönde gelişir. Yani
negatif yük, elektrik alan doğrultusunda hareket ettiği zaman elektriksel
potansiyel kazanır ve elektrik alan içinde durgun halden serbest
bırakılırsa, elektrik alana zıt doğrultuda ivmelenir.
Şimdi, şekildeki gibi, 𝑥 ekseni boyunca yönelmiş düzgün bir elektrik
alan içinde, herhangi iki nokta arasında bir dış etken olmadan hareket
eden bir yüklü parçacığın daha genel durumunu inceleyelim. A ve B
noktaları arasındaki yer değiştirme vektörü 𝒔 ile gösterilirse iki nokta
arasındaki potansiyel fark aşağıdaki gibi ifade edilmektedir (Elektrik
alanı E sabittir).
Yükün potansiyel enerjisindeki değişim ise;
Şimdi 𝑬 ∙ 𝒔 skaler çarpımını inceleyelim. 𝑬 elektrik alan vektörü ile 𝒔
vektörü arasındaki açı 𝜃 olmak üzere 𝒔 vektörü 𝒔 = 𝑨𝑪 + 𝑪𝑩 vektörü
ile temsil edilebilir.
𝑨𝑪 vektörü ile 𝑬 vektörü arasındaki açı 𝜃 = 0 dır ve bu durumda
skaler çarpım sonucu − 𝑬 ∗ 𝑨𝑪 elde edilirken 𝑪𝑩 vektörü ile 𝑬
vektörü arasındaki açı 𝜃 = 90 dır ve bu durumda skaler çarpım
sonucu sıfırdır.
Bu nedenle 𝑉𝐵 − 𝑉𝐴 potansiyel farkı 𝑉𝐶 − 𝑉𝐴 potansiyel farkına eşit
olup 𝑉𝐵 = 𝑉𝐶 dir. Bu nedenle aynı potansiyele sahip olan noktaların
sürekli dağılımlarının oluşturduğu herhangi bir yüzeye eş potansiyel
yüzey adı verilir.
Örnek Zıt Yüklü İki Paralel Levha Arasındaki Elektrik Alanı
Batarya, belirli bir potansiyel farkını batarya kutuplarına bağlanmış
iletkenler arasında oluşturan bir elektriksel cihazdır. 12 V’luk bir
batarya, iki paralel levha arasına şekildeki gibi bağlanıyor. Levhalar
arasındaki uzaklığın 𝑑 = 0,30 𝑐𝑚 ve elektrik alanının düzgün olduğu
varsayılıyor. Levhalar arasındaki elektrik alanın şiddetini bulunuz.
Örnek Bir Protonun Düzgün Bir Elektrik Alan İçindeki Hareketi
Bir proton, pozitif 𝑥 ekseni doğrultusu boyunca yönelen 8,0 ×
104 𝑉/𝑚 lik düzgün bir elektrik alan içinde durgun halden serbest
bırakılıyor. Proton bu elektrik alanın etkisiyle 0,50 𝑚 yer değiştiriyor.
Buna göre A ve B noktaları arasındaki elektriksel potansiyeldeki
değişimi ve protonun potansiyel enerjisindeki değişimi bulunuz.
Elektriksel Potansiyel ve Noktasal
Yüklerin Oluşturduğu Potansiyel Enerji
Şekilde gösterilen noktasal artı 𝑞
yükünden 𝑟
uzaklıkta bir noktada
elektriksel potansiyeli bulmak için
keyfi
olarak
seçilen
A
ve
B
noktalarının potansiyel farklarından
yararlanılmaktadır.
potansiyel
gibidir.
fark
Bu
ifadesi
durumda
aşağıdaki
Noktasal yükün oluşturduğu elektrik alanı
𝑬 = 𝑘𝑒 𝑞𝒓/𝑟 2 olduğundan
𝑬 ∙ 𝑑𝒔 skaler
çarpımı aşağıdaki gibi ifade edilebilir.
Burada tanımlanan 𝒓 vektörü yükten
elektrik alanının hesaplanacağı noktaya
yönelen birim vektör olup büyüklüğü
birdir.
Bu durumda skaler çarpımı sonucu
𝒓 ∙ 𝑑𝒔 = 𝑑𝑠 ∗ 𝑐𝑜𝑠(𝜃) olur. Burada ifade
edilen 𝜃 açısı şekilde gösterildiği gibi 𝒓
ile
𝑑𝒔
arasındaki
açıdır.
Ayrıca
𝑑𝑠 ∗ 𝑐𝑜𝑠(𝜃) değeri, 𝑑𝒔 vektörünün 𝒓
vektörü
üzerindeki
𝑑𝑠 ∗ 𝑐𝑜𝑠 𝜃 = 𝑑𝑟
edilebilmektedir.
izdüşümü
olup
olarak
ifade
Dolayısıyla
potansiyel
ifadesindeki
𝑬 ∙ 𝑑𝒔
(𝑘𝑒 𝑞/𝑟 2 )𝑑𝑟
fark
yerine
yazılır ve integral
işlemleri yapılırsa aşağıdaki sonuç
elde edilir.
Elde edilen bu matematiksel ifade bize aşağıda yazılı önemli sonuçları
gösterir.
1. −
𝐵
𝑬
𝐴
∙ 𝑑𝒔 integrali A ve B noktaları arasındaki yoldan bağımsızdır.
2. A ve B gibi herhangi iki nokta arasındaki potansiyel farkı, yalnızca
𝑟𝐴 ve 𝑟𝐵 radyal koordinatlara bağlıdır.
3. 𝑟𝐴 = ∞ da, referans elektriksel potansiyeli sıfır olarak seçilebilir.
4. Böyle bir seçim yapıldığında (yani 𝑟𝐴 = ∞ iken) bir noktasal
yükün kendisinden herhangi bir 𝑟 uzaklıkta oluşturduğu potansiyel
aşağıdaki gibi ifade edilebilir.
İki veya daha fazla nokta yükün bir P noktasında oluşturduğu toplam
elektriksel potansiyel, her bir yükün bu noktada oluşturduğu
potansiyellerin cebirsel toplamıdır.
Yukarıdaki denklem incelendiğinde toplam ifadesinin vektörel
toplamdan
ziyade
görülmektedir.
skaler
sayıların
cebirsel
toplamı
olduğu
İki Yüklü Parçacık Sisteminin Potansiyel Enerjisi
Aşağıdaki iki parçacıklı sistemde yükler arasında 𝑟12 kadar uzaklık
varsa bu sistemin potansiyel enerjisi (yani yüklerden birinin diğerinin
yanına getirebilmek için yapılması gereken iş) aşağıdaki gibi ifade
edilir.
Sistemde ikiden fazla yük varsa, toplam potansiyel enerji her bir
yük çifti için potansiyel enerji ayrı ayrı hesaplanarak sonuçlar
cebirsel olarak toplanır.
Örnek İki Nokta Yükün Elektriksel Potansiyeli
Şekilde görüldüğü gibi, 𝑞1 = 2,00 𝜇𝐶 ’ luk yük orijinde iken
𝑞2 = −6,00 𝜇𝐶’ luk yük (0,00 ; 3,00) m koordinatındadır.
(a) Bu yüklerin (4,00; 0) m koordinatında buluna bir P noktasında
oluşturmuş olduğu toplam elektriksel potansiyeli bulunuz.
(b) Sonsuzdan P noktasına getirilen 3,00 𝜇𝐶′luk yükün potansiyel
enerjisindeki değişimi bulunuz.
ELEKTRİK ALAN DEĞERİNİN
ELEKTRİKSEL POTANSİYELDEN ELDE EDİLMESİ
Belirli bir bölgede elektriksel potansiyel biliniyorsa, elektriksel alan
değerinin hesaplanabilmesi için aralarında 𝑑𝑠 kadar uzaklık bulunan
iki noktasal yükün aşağıda ifade edilen 𝑑𝑉 potansiyel farkından
yararlanılır.
Eğer elektrik alanının yalnızca 𝐸𝑥 bileşeni varsa (x doğrultusundaki
bileşeni), 𝑬 ∙ 𝑑𝒔 = 𝐸𝑥 𝑑𝑥 olur ve böylece elektrik alanın 𝐸𝑥 bileşenin
büyüklüğü aşağıdaki gibi tanımlanır.
Bu durumda bir koordinat ekseni doğrultusundaki elektrik alanın
büyüklüğü, bu koordinata göre elektriksel potansiyelin türevinin
negatifine eşittir.
Eğer elektrik alanı oluşturan yük dağılımı küresel simetriye sahipse,
yani hacimce yük yoğunluğu yalnız 𝑟 radyal (yarıçapsal) uzaklığa
bağlı ise; o zaman elektrik alanı da radyaldır denir. Bu durumda,
𝑬 ∙ 𝑑𝒔 = 𝐸𝑟 𝑑𝑟 olur ve böylece 𝑑𝑉 = −𝐸𝑟 𝑑𝑟 ifadesinden elektrik
alanının büyüklüğü aşağıdaki gibi ifade edilir.
Örneğin, bir noktasal yükün elektriksel potansiyeli 𝑉 = 𝑘𝑒 𝑞/𝑟 ile
ifade edilmektedir. Dolasıyla noktasal yükün oluşturduğu elektrik
alanın büyüklüğü 𝐸𝑟 = 𝑘𝑒 𝑞/𝑟 2 olarak hesaplanır.
Eğer 𝑑𝑉 = −𝑬 ∙ 𝑑𝒔 = 0 ise
1. 𝑑𝑉 = 0 dır. Yani tanımlanan bir yol boyunca potansiyel fark
yoktur (𝑑𝑉𝐵 − 𝑑𝑉𝐴 =0). O zaman tanımlanan bu yol aşağıdaki
şekilde gösterildiği gibi (mavi kesikli çizgiler) eşpotansiyel
çizgileridir.
2. −𝑬 ∙ 𝑑𝒔 = 0 = − 𝑬 𝑑𝒔 cos(90°) dır. O zaman tanımlanan yolda
elektrik alanı bu yola diktir.
Sonuç: Eşpotansiyelli yüzeyler elektrik alan çizgilerine daima diktir
denir.
Aşağıdaki şekilde bir elektrik dipolünün eş potansiyel yüzeyleri mavi
çizgilerle gösterilmiştir. Bir deneme yükü, eşpotansiyelli yüzeyde bir
𝑑𝒔 yerdeğiştirmesi yaptığında 𝑑𝑉 = 0 olur çünkü eşponsiyelli
yüzeylerde potansiyel sabittir. O halde 𝑬 elektrik alan vektörü,
eşpotansiyelli yüzey boyunca yerdeğiştirmeye dik olmak zorundadır.
Bu sonuç, eşpotansiyelli yüzeylerin her zaman elektrik alan
çizgilerine dik olduğunu gösterir.
Genel olarak elektriksel potansiyel, üç uzaysal koordinatın bir
fonksiyonu cinsinden verilirse 𝑉(𝑥, 𝑦, 𝑧) elektrik alan vektörünün
bileşenleri (𝐸𝑥 , 𝐸𝑦 , 𝐸𝑧 ) potansiyel fonksiyonunun kısmı türevleri
alınarak aşağıdaki gibi tanımlanabilir.
Örnek Bir Dipolün Elektriksel Potansiyeli
Eşit ve zıt işaretli iki yükten oluşan elektrik
dipolünde yükler arasındaki uzaklık 2𝑎 dır.
(a) P noktasındaki elektriksel potansiyeli
hesaplayınız.
(b) Dipolden çok uzak bir noktada 𝑉 ve 𝐸𝑥 ’ i
hesaplayınız.
Sürekli Yük Dağılımının Oluşturduğu Elektriksel Potansiyel
Sürekli bir yük dağılımının bir P noktasında oluşturduğu elektriksel
potansiyeli, yüklü cismi çok küçük 𝑑𝑞 yük elemanlarına bölerek ve
bütün bu yük elemanlarının potansiyele katkılarını toplayarak
hesaplayabiliriz. Şekilde görülen 𝑑𝑞 yük elemanının oluşturduğu 𝑑𝑉
potansiyeli aşağıdaki gibi tanımlanır.
Her bir yük elemanı P noktasından farklı uzaklıklarda olması
nedeniyle yük dağılımının bir P noktasında oluşturduğu elektriksel
potansiyeli ifadesi aşağıdaki gibi hesaplanabilir.
Örnek Düzgün Olarak Yüklenmiş Bir Halkanın Potansiyeli
Toplam yükü 𝑄 ve yarıçapı 𝑎 olan düzgün yüklenmiş bir halkanın
(a) Merkezinden geçen çapına dik eksen üzerindeki bir P
noktasındaki elektriksel potansiyeli bulunuz.
(b) P noktasındaki elektrik alanının büyüklüğünü belirleyiniz.
Örnek Sonlu Çizgisel Yükün Elektriksel Potansiyeli
𝑙 uzunluklu bir çubuk, 𝑥 ekseni boyunca yerleştiriliyor. Çubuktaki
toplam yük 𝑄 dur ve birim uzunluk başına düzgün dağılmış yük
yoğunluğu λ = 𝑄/𝑙 dir. 𝑦 ekseni boyunca, orijinden 𝑎 uzaklıktaki bir
P noktasında elektriksel potansiyeli bulunuz.
Örnek Düzgün Yüklenmiş Bir Diskin Potansiyeli
Yüzeyindeki yük yoğunluğu σ, yarıçapı 𝑎 olan düzgün yüklenmiş bir
diskin merkezinden dik geçen eksen boyunca
(a) Elektriksel potansiyeli bulunuz
(b) Elektrik alanın büyüklüğünü bulunuz.
Örnek Düzgün Yüklenmiş Bir Kürenin Potansiyeli
Düzgün dağılmış pozitif bir yük yoğunluğuna sahip, toplam yükü 𝑄
olan 𝑅 yarıçaplı yalıtkan bir küre veriliyor.
(a) Kürenin dışındaki bir noktada, yani 𝑟 > 𝑅
de elektriksel
potansiyeli bulunuz. 𝑟 = ∞ da potansiyeli sıfır olarak alınız.
(b) Yüklü kürenin içindeki elektriksel potansiyeli bulunuz. Yani
𝑟 < 𝑅 için.
KAYNAK
• Fen ve Mühendislik İçin FİZİK-2
Serway.Beichner Palme Yayıncılık