bağımsız kaynaklar

DEVRE TEOREMLERİ
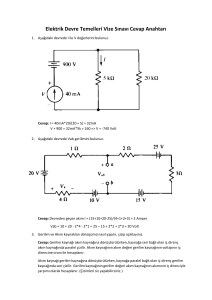
1
Lineerlik Özelliği
• Etki ile tepki arasındaki ilişki eğer doğrusal
şekilde tanımlanabiliyorsa, bu ilişkiyi
sağlayan eleman lineerdir.
• Bir devrenin girişi ile çıkışı arasında lineer
(doğrusal) bir ilişki varsa –yani giriş ile
çıkış birbiri ile doğrudan orantılı ise-bu
devreye lineer devre denir.
2
Örnek:
Eger
Is  15A, ise
Io  3A;
Eger
Is  5A, ise
Io  1A.
3
Süperpozisyon (Toplamsallık)
• Toplamsallık özelliği; lineer bir devredeki
bir eleman üzerindeki gerilim düşümü (veya
akım geçişi) o devredeki herbir bağımsız
kaynağın o eleman üzerindeki etkilerinin
(gerilim düşümü veya akım geçişi) cebirsel
toplamına eşittir şeklinde ifade edilir.
4
Süperpozisyon (Toplamsallık)
• Süperpozisyon yönteminin uygulama
adımları:
1. Devredeki biri hariç tüm kaynaklar kaldırılır
(Akım kaynakları açık devre, Gerilim kaynakları
kısa devre) ve çıkış bilinen devre analizi
yöntemleri kullanılarak belirlenir.
2. Tüm kaynaklar için Adım 1 tekrar edilir.
3. Devre dışı bırakılarak teker teker etkileri
hesaplanmış olan kaynaklardan elde edilen
ifadeler cebirsel olarak toplanır.
5
j
i
e
+
L N
R1
V
-
j
i1
L N
+
V1
-
i2
R1
e
L N
+
R1
V2
-
V  V 1  V 2; i  i1  i 2
6
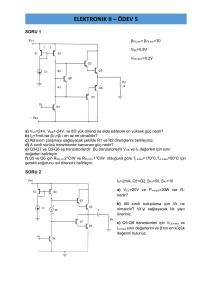
Örnek
v  v1  v2
v1  2V ; v 2  8V
 v  10V
7
Kaynak Dönüşümü
• Kaynak dönüşümü, bir gerilim kaynağına “Vs”
seri bağlı bir dirençten “R” oluşan kaynağı, bir
akım kaynağı “is” ve buna paralel bağlı bir direnç
“R” formuna dönüştürme işlemidir. Bu işlem her
iki yönlüdür.
Vs=isR
veya
is=Vs/R
8
Kaynak Dönüşümü
•Bu işlem aynı zamanda bağımlı kaynaklara
da uygulanabilir:
Bağımlı kaynak: Bir kaynak (akım veya gerilim) devredeki
diğer elemanlardan birisine bağlı bir şekilde değişim
gösteriyor ise bu kaynak bağımlı kaynaktır.
9
Örnek, Vo=?
10
Böylece, vo=3.2V olarak bulunur.
11
Örnek: Kaynak dönüşümü kullanarak I değerini hesaplayınız.
2A
I
2A
6V
7
I  0.5 A
12
Substitution (Yerine Kullanma)
Teoremi
• İki taraflı bir DC devrenin (ağın) herhangi
bir dalındaki gerilim ve akım ifadesi
biliniyor ise, bu dal farklı elemanların farklı
kombinasyonları şeklinde oluşturulabilecek
farklı bir devre ile değiştirilebilir. Öyleki
yeni devre seçilen dal için aynı akım ve
gerilim ifadesini sağlamalıdır.
13
Substitution (Yerine Kullanma)
Teoremi
Is
+
Vs
N
N1
N2
-
Vs
N1
Is
OR
N
N1
14
Substitution (Yerine Kullanma)
Teoremi
I1
6
I3
+
I2
8
V3
20V
-
I1=2A,
I2=1A,
I3=1A,
V3=8V
I1
4
6
4V
20V
I1
I3
I3
+
+
I2
8
V3
6
8V
I2
8
V3
1A
20V
-
-
I1=2A,
I2=1A,
I3=1A,
V3=8V
I1=2A,
I2=1A,
I3=1A,
V3=8V
15
Thevenin Teoremi
• İki uçlu lineer bir devre bir gerilim kaynağı
“Vth” ile buna seri bağlı bir direnç “Rth” ile
gösterilebilir. Burada Vth gerilim kaynağı iki
uçlu devrenin açık devre gerilimi, Rth
direnci ise bağımsız kaynaklar devre dışı
bırakıldığı zamanki eşdeğer direnç değeridir.
16
(a) orjinal devre, (b) Thevenin eşdeğer devresi
c
d
17
Şekillerle ispat
I
+
V
LN
LOAD
LN
-
LN
I
+
V
I
-
+
Voc
-
+
LNo
+
RoI
Is
-
V=Voc-RoI
18
Thevenin Teoremi
Rth direnç değeri bulunurken iki durum göz önüne alınır:
•
Durum 1 Eğer devre (ağ) bağımlı kaynak
içermiyorsa, tüm bağımsız kaynaklar devre dışı
bırakılır ve çıkışın sol tarafında kalan eşdeğer direnç
hesaplanır.
•
Durum 2 Eğer devrede bağımlı kaynaklar varsa
eşdeğer direnç Rth iki yol ile hesaplanır:
19
Thevenin Teoremi
•
Durum 2 Eğer devrede bağımlı kaynaklar varsa
eşdeğer direnç Rth iki yol ile hesaplanır:
1. Devredeki tüm bağımsız kaynaklar devre dışı
bırakıldıktan sonra, a ve b uçlarına v0 değerlikli bir
gerilim uygulanır ve kaynaktan çekilen i0 akımı
belirlenir (veya tam tersi). Buradan Rth= v0/ i0
hesaplanır.
20
Thevenin Teoremi
2.
Devrenin açık devre gerilimi Voc ile kısa devre akımı Isc
hesaplanır ve buradan Rth=Voc/Isc değeri bulunur.
Original
+
Voc
Circuit
Original
Isc
Circuit
Rth=Voc/Isc
-
21
ÖRNEK
AŞAĞIDAKİ DEVRENİN THEVENİN EŞDEĞERİNİN BULUNMASI
KCL @V1 :
V1
VP
V1 V1  2VX V1  VP


0
1k
2k
1k
Bağımlı değişkenin Tanımı:
4
V1  VP ,
7
VX  VP  V1
3
VX  VP
7
VP VP  2VX VX
IP 


2k
1k
1k
IP 
VP
RTH 
15VP
14k
VP 14
 k
I P 15
IP
22
Norton Teoremi
• İki uçlu lineer bir devre bir akım kaynağı
“IN” ile buna seri bağlı bir direnç “RN” ile
gösterilebilir. Burada IN akım kaynağı iki
uçlu devrenin kısa devre akımı, RN direnci
ise bağımsız kaynaklar devre dışı
bırakıldığı zamanki eşdeğer direnç değeridir.
23
(a) Orjinal devre, (b) Norton eşdeğeri
N
(c)
d
24
Maksimum Güç Transferi
Orjinal ağın yerine Thevenin eşdeğerinin yerleştirilmesi ile elde
edilen devrede yüke (LOAD) aktarılan güç:
VTh
p  i RL  (
) 2 RL
RTh  RL
2
LN
I
+
V
a
RL
b
25
Yüke aktarılan güç RL nin bir fonksiyonudur ve:
dp
2  RTh  RL  
 TTh 
0
3
dRL
 RTh  RL  
bu esitlik sadece RL  RTh
icin saglanıa ve
VTh2
p
4 RTh
ÖDEV: Bu şartın böyle olduğunu
lütfen ispat edin ve VTh=No+5V,
RTh=No+5k için MATLAB de soldaki
eğriyi elde edin
d2p
0
2
dRL
26
BUNDAN SONRASINI
TERCUME ET
•
If the load RL is invariable, and RTh is variable,
then what should RTh be to make RL get
maximum power?
• If using Norton equivalent to replace the original
circuit, under what condition does the maximum
transfer occur?
• Is it true that the efficiency of the power transfer
is always 50% when the maximum power transfer
occurs?
27
Maximum Power Transfer
(several questions)
•
If the load RL is invariable, and RTh is variable,
then what should RTh be to make RL get
maximum power?
• If using Norton equivalent to replace the original
circuit, under what condition does the maximum
transfer occur?
• Is it true that the efficiency of the power transfer
is always 50% when the maximum power transfer
occurs?
28
Examples
29
Tellegen Theorem
• If there are b branches in a lumped circuit,
and the voltage uk, current ik of each branch
apply passive sign convention, then we have
b
u
k 1
i 0
k k
30
Inference of Tellegen Theorem
• If two lumped circuits N and N̂ have the same topological
graph with b branches, and the voltage, current of each
branch apply passive sign convention, then we have not
only
b
u i
k 1
k k
b
 uˆ iˆ
0
k 1
b
but also
 uˆ i
k 1
k k
k k
0
0
b
 u iˆ
k 1
k k
0
31
Example
N is a network including resistors only. When R2  2, V1  6V ,
We can get I1  2 A, V2  2V ; When R2  4, V1  10V , We can
get I1  3 A, find out V2 then.
I1
N
V1
According to the Tellegen Theorem
I2
R2
+
V2
-

b
V I   V I
k 3
k k
k 3
k k
b
k 3
k 3
V1 I1  V2 I 2  Vk I k  0 ; V1I1  V2I 2   VkI k  0
and Vk I k  RI k I k  RI k I k  VkI k
b
b
 V1 I1  V2 I 2  V1I1  V2I 2
V2
2
6  (3)  2   10  (2)  V2 
4
2
 V2  4V
32
Reciprocity Theorem
R1
4V
Vs
2
R2
6
R3
3
1
I2  A
3
I2
I2
R1
R2
2
6
R3
3
Vs
4V
1
I2  A
3
33
Reciprocity Theorem
(only applicable to reciprocity networks)
• Case 1
The current in any branch of a network, due to a single
voltage source E anywhere else in the network, will equal the
current through the branch in which the source was originally
located if the source is placed in the branch in which the current I
was originally measured.
N
Vs
I2
if
Vs  Vs' then I1'  I 2
actually exists :
I1'
N
I1' I 2

Vs' Vs
V s'
34
Reciprocity Theorem
(only applicable to reciprocity networks)
Case 2
Is
N
if
+
Is  Is ' then V 1'  V 2
V2
-
actually exists :
+
N
V 1' V 2

Is ' Is
Is'
V1'
-
35
Reciprocity Theorem
(only applicable to reciprocity networks)
Case 3
N
+
if
V2
-
Vs
Vs  Is ' then I1'  V 2
actually exists :
I1'
N
I1' V 2

Is ' Vs
Is'
36
example
37
Source Transfer
•
Voltage source transfer
R2
R4
R1
Vs
R2
R4
Vs
R5
R1
R5
R3
Vs
R3
An isolate voltage source can then be transferred to a
voltage source in series with a resistor.
38
Source Transfer
•
Current source transfer
R2
R3
C
R2
C
R3
Is
Is
Is
B
R1
A
R4
B
R1
A
R4
Examples
39
Summary
•
•
•
•
•
•
Linearity Property
Superposition
Source Transformation
Substitution Theorem
Thevenin’s Theorem
Norton’s Theorem
• Maximum Power
Transfer
• Tellegen Theorem
• Inference of Tellegen
Theorem
• Reciprocity Theorem
• Source Transfer
40