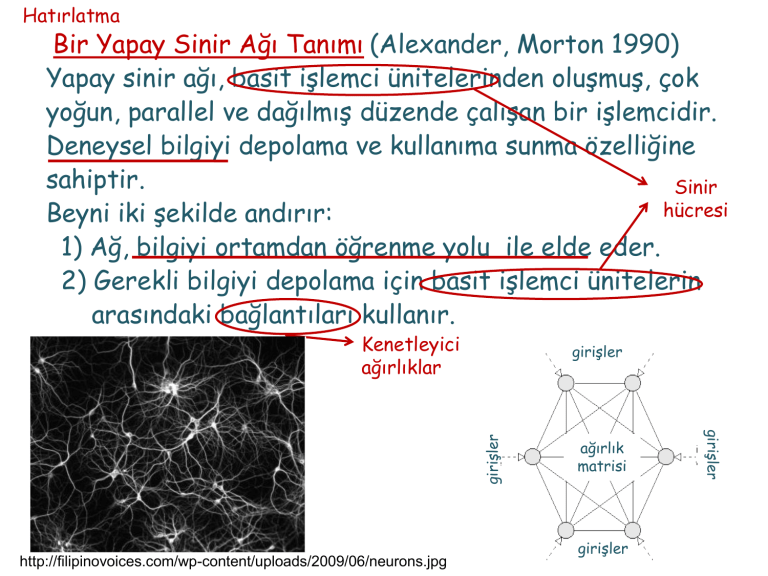
Hatırlatma
Bir Yapay Sinir Ağı Tanımı (Alexander, Morton 1990)
Yapay sinir ağı, basit işlemci ünitelerinden oluşmuş, çok
yoğun, parallel ve dağılmış düzende çalışan bir işlemcidir.
Deneysel bilgiyi depolama ve kullanıma sunma özelliğine
sahiptir.
Sinir
hücresi
Beyni iki şekilde andırır:
1) Ağ, bilgiyi ortamdan öğrenme yolu ile elde eder.
2) Gerekli bilgiyi depolama için basit işlemci ünitelerin
arasındaki bağlantıları kullanır.
Kenetleyici
ağırlıklar
http://filipinovoices.com/wp-content/uploads/2009/06/neurons.jpg
ağırlık
matrisi
girişler
girişler
girişler
girişler
Hatırlatma
Ağ Yapıları
İleri yol
Tam bağlaşımlı
Karma
girişler
girişler
girişler
ağırlık matrisi
ağırlık
matrisi
girişler
gizli katman
girişler
ağırlık matrisi
ağırlık
matrisi
çıkış katmanı
çıkışlar
girişler
http://fbim.fh-regensburg.de/~saj39122/jfroehl/diplom/e-12-text.html
öznitelik dönüşümü
Hatırlatma
Öğrenme Süreçleri
Ağın içinde bulunduğu ortamdan etkilenerek parametrelerini
değiştirmesi işlemi öğrenmedir.
Öğrenme şekli,
parametrelerin nasıl değiştirildiği ile belirlenir.
Öğrenme Süreçleri
Eğiticili Öğrenme
Eğiticisiz Öğrenme
Pekiştirmeli
Öğrenme
Özdüzenlemeli
Öğrenme
Hatırlatma
Eğiticili Öğrenme
Ortam
x
Eğitici
yd
+
Eğitilen Sistem
y
e
Hatırlatma
Özdüzenlemeli Öğrenme
Ortam
Eğitilen Sistem
Hatırlatma
Pekiştirmeli Öğrenme
Eğitilen Sistem
δ
Kritik
Değer Atama
Ödül r
Ortam
davranış
“Bilgi”’nin Gösterimi
“Bilgi” İnsan
veya
Makina
Nasıl anlayacağız?
Yorumlama
Öngörme
Uygun yanıt
verme
Depolanmış
enformasyon
veya
model
Nasıl gösterimi oluşturacağız?
Kurallar: (1) Benzer sınıflardan benzer girişler ağda
benzer gösterimler oluşturmalı ve böylece
aynı kategoriye ait olarak sınıflanmalı,
(2) Farklı sınıflara ayrılacak nesnelere, ağda
çok farklı gösterimler atanmalı,
(3) Belirli bir özellik önemli ise ağda onun
gösterimi ile görevlendirilen hücre sayısı
daha fazla olmalı,
Benzerliğin bir ölçütü - Norm
V vektör uzayı olmak üzere, aşağıdaki dört özelliği sağlayan
fonksiyon . :V R normdur
x 0
x 0 x0
x x
x y x y
Gösterim için bir yol
İşlem uygulayacağımıza göre
nasıl ifade edebiliriz?
Bir T harfi
Bir L harfi
1
0
0
1
L 0
0
1
1
1
1
1
1
0
T 1
0
0
1
0
İleri Yol Ağı ve Eğiticili Öğrenme
x1
x1
h11
h11
1
h2
x2
x2
xn
1
y11
y11
1
2
y
1
1hm y1m
2 11
2
h
y
Giriş vektörü
h12
h1ç
h12
h1ç
h22
h2ç
y2
hk2
2
2
h
hlç
1
1
h2ç
y1
yl
y2
Gizli katmanlar
Çıkış katmanı Çıkış vektörü
y Rl
x Rn
xn
y1
hm1
y
1
1
m
hk2
hlç
1
yl
Çok Katmanlı Algılayıcı-ÇKA
(Multi-Layer Perceptron)
Teorem: (Kolmogorov 1957)
f ( x1, x2 ,..., xn )
g ij (.)
h j (.)
xi [0,1]n , n 2
f ( x1 , x2 ,..., xn ) ‘e bağlı olmayan
monoton artan
sürekli
tek değişkenli fonksiyon
sürekli
tek değişkenli fonksiyon
n
f ( x1 , x2 ,..., xn ) h j gij xi
j1
i 1
2n1
Teoremin sonuçları.....
• Kolmogorov Teoremi bir varlık teoremi
f ( x1 , x2 ,..., xn ) ‘i özel bir şekilde ifade edebileceğimizi
söylüyor.
g ij (.)
ve
h j (.) ‘nin ne yapıda olduklarını ve kaç tanesinin
yeterli olacağını söylüyor.
• Kolmogorov Teoremi bir varlık teoremi olduğundan
h j (.) nasıl belirlenir söylemiyor.
g ij (.),
Kolmogorov Teoreminde bazı şeylerden vazgeçelim, tam
olmasın yaklaşık olsun ama fonksiyonları bilelim.
Teorem: (Cybenko 1989)
N yeterince büyük, j R , herhangi bir sürekli sigmoid
N
fonksiyon
T
f ( x1 , x2 ,..., xn ) ~
j w j x j
j1
df
a, b R ve a b f : R R
0
dx
lim f ( x) a lim f ( x) b
f
x
Giriş
x
Gizli katman Gizli
1
katman 2
Çıkış
http://www.oscarkilo.net/wiki/images/8/84/Ffperceptron.png
sigmoid
• Ağ yapısı
giriş katmanı
işlem yapan gizli katmanlar
işlem yapan çıkış katmanı
• Nöron
sürekli türetilebilir,
lineer olmayan aktivasyon
fonksiyonu var
• Eğitim
eğiticili öğrenme
• Öğrenme algoritması
geriye yayılım
x
x1
y1 ( w1 x)
y2 ( w2 y1 )
x2
y ( wo y )
2
xn
e
- +
yd
Gizli katman ve çıkış katmanındaki her nöron iki iş yapıyor:
(i) nöron çıkışındaki işareti nöron girişindeki işaretler
cinsinden hesaplıyor,
(ii) gradyen vektörünü geriye yayılım için yaklaşık olarak
hesaplıyor
Eğitim Kümesi
x
q
x , y
q
P
q
d
P
q 1
q 1
y
q
d
T2
T1
L1
L2
T3
P
q 1
T,L
L3
Giriş vektörü
İstenilen Çıkış vektörü
xR
yd R
T1 1 1 1 1 n 1 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0' lT 0 1'
L1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 1 1 1' L 1 0'
x1
x2
h11
y11
1
h2
1
2
y
h12
h1ç
y1
e1
h22
h2ç
y2
yd 1
e2
yd 2
xn
x1
x
2
x
1
x2
xn
1
y1
xny12
1
ym
1
v11
1
v2
1
vm
1
hm
y1
m
1
hk2
hlç
el
1
y1
y12
v12
2
2
y2
y2
v2
x1
1
1
w12 ... w1( n1)
1
y
1 2
1
x
2
w22vk ... w12(ynk1) 2 (.) yy1l
1
2
y1
2
2
w1 12 ... w1 1( n1)xn 1
2
y
1
wm 22
wm2( n1) y2
ym2
w
...
w
(.)
1
22
2 ( n 1)
2
y2
1
2
ym
2
2
2
2
w
w
w
v
k k1 k 2
k ( n 1)
y k
1
y11
1
y2
v11 w111
1 y1 1
v2 mw21
2 2
1v1 w
1 11
vmv2 ww
m12
21
yl
ydl
x1
x2
h11
y11
1
2
h
y1
2
h12
h1ç
2
2
ç
2
h
h
e1
y1
yd 1
y2
e2
yd 2
xn
1
1
hm
y1
m
hk2
hlç
1
el
1
xx11q
1
2
1
2
Kümesindeki
q. çifte
ilişkin
çıkış
xEğitim
y
y
v
v
1
1
1
1
q
q
q
q
2
j.
nörondaki
hata:
xkatmanındaki
e
y
y
1
2
2
1
2
j
dj
j
y
y
v
v
2
2
2
2
1
q 2
Nöron
j için ani
(
e
hata:
j)
2
2
1
1
2
ym
vm
vk l y k
xnq
xnToplam
ani hata: ( q ) 1
(e qj ) 2
2 j 1
Ortalama karesel hata:
yl
ort
1
p
p
q 1
(q)
ydl
y1 yddq11 y11 e1q
y q y q
e2
22
y2 dd 22
q
q
ylydldl yll el
Eğiticili Öğrenme
Amaç Ölçütü
Toplam ani hata:
(q)
1
2
l
(e qj ) 2
j 1
veya
Ortalama karesel hata:
ort
1
p
p
q 1
olan bir eniyileme problemi
min
wij R
(q)
( k 1)
Öğrenme kuralı: w ji
1
min
wij R 2
(e )
j 1
l
(k )
E
w(jik ) ( k )
w ji
q 2
j
(q)
1
E
2
l
1
ej
2
j 1
2
y
l
j 1
dj
yj
ç
e
y
v
E
E j
j
j
wçji e j y j v çj wçji
2
1
2
yd
j
j 1
l
r
i 1
w y
2
ç ç 1
ji i
E
ç
ç 1
e
(
1
)
(
v
)
y
j
j
i
wçji
çj
Yerel gradyen
1ç e1 1 (v1ç )
ç 1 ç
2 ˆ e2 (v2 )
ç 1 ç
l el (vl )
h11
x1
y11
1
2
h
x2
y1
2
h12
h1ç
2
2
ç
2
h
h
e1
y1
yd 1
y2
e2
yd 2
1
hm
xn
1
y1
m
hk2
hlç
1
yl
el
1
ydl
E
w (k 1) w (k ) ç wçji (k ) çj (k ) yiç 1 (k )
11
12 w ji k
1ç
yd 1 y1 e1
ç11
ç21
E
yç2 y
ç 1 ç
ç 1
w
(
k
1
)
w
(
k
)
w
(
k
)
(
k
)
yi d 2 (k ) 2 e2
ji 2
ji 2
j
ç 1
ji2
w ji
k
1
2
ç
ydl yl el
E
w
2
2
2
2
1
jil(k 1) w ji l(k)
l j(k ) yi (k )
w
(
k
)
ji
w2ji
ç
ji
ç
ji
k
E
w (k 1) w (k ) 1
w ji
1
ji
w1ji (k ) 1j (k ) xi (k )
1
ji
k












