Teorem: Lagrange İnterpolasyon Polinomu

22,6
22,5
22,4
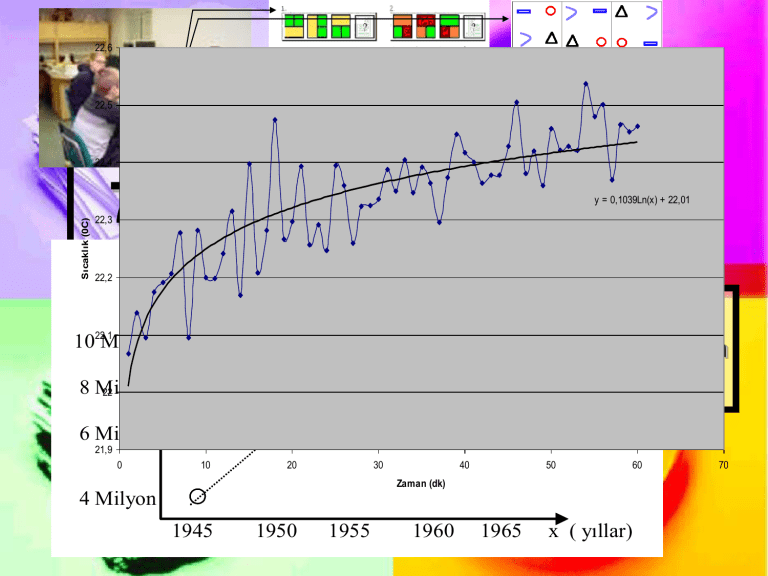
7) İNTERPOLASYON
Sıcaklık (0C)
y = 0,1039Ln(x) + 22,01
22,3
istatistiksel veriler
f(x)
Nüfus
22,2
22,1
10 Milyon
8 Milyon
22
İnterpolasyon, eldeki verilerin dağılımından
yararlanarak, elde olmayan bir değerin tahmin
edilmesi olarak özetlenebilir.
?
6 Milyon
21,9
0
10
20
30
40
50
60
Zaman (dk)
4 Milyon
1945
1950
1955
1960
1965
x ( yıllar)
70
İnterpolasyon ve eğri uydurma
Armatür
Giriş
Sistem
Çıkış
Ra
Va
x
La
ia
x
Vb
y
y=f(x)
Rf
Lf
+
y1
x2
y2
x3
y3
x4
y4
x5
y5
x6
y6
w,
y
if (t)
Alan Akımı
-
x1
Armatür Akımı
Yük
J=Eylemsizlik
b=sürtünme
Sistem veya fonksiyonun karakteristiğini
betimleyen bir polinom elde edilir
Serhat YILMAZ, Kocaeli Üniversitesi, Elektronik
ve Haberleşme Bölümü
y=P(x)=2x3-9x2+x+10
2
İnterpolasyon-eğri uydurma?
Ne fark var?
f(x)
---------Doğrusal İnterpolasyon
Eğri Uydurma
x
Şekil.7.1. İnterpolasyon ve Eğri Uydurma Grafikleri
Serhat YILMAZ, Kocaeli Üniversitesi, Elektronik
ve Haberleşme Bölümü
3
7.1. Doğrusal İnterpolasyon

Koordinatları (x1,y1), (x2,y2) olarak verilen iki noktadan bir
doğru geçer ve denklemi;
x  x1
y  y1

x 2  x1 y 2  y1
y
x  x 2 
x  x1 
y1 
y2
x1  x2 
x2  x1 
Örnek: Verilen noktalardan geçen fonksiyonu bulunuz.
x1=0, x2=1, y1=3, y2=5
x
f(x)
0
3
x  1 3  x  0 5 =2x+3
y
1
5
0  1 1  0
Serhat YILMAZ, Kocaeli Üniversitesi, Elektronik
ve Haberleşme Bölümü
4
7.2. Lagrange Polinom İnterpolasyonu
Şekil.7.2. N noktadan N-1. dereceden bir polinom geçebilir
Lagrange interpolasyon formülü, N noktadan geçen N-1
dereceli polinomu tanımlayan bir teoremle verilir.
Serhat YILMAZ, Kocaeli Üniversitesi, Elektronik
ve Haberleşme Bölümü
5
Teorem: Lagrange İnterpolasyon
Polinomu

Koordinatları (x1,y1),(x2,y2),.......(xN , yN) olan noktalar, derecesi en
fazla N-1 olan,
N
P(x)=L1(x) y1+ L2(x) y2+...................... LN(x) yN =  Lk ( x) y k
k 1
tanımlar
Lk(x)=
N
x  xi 
x  x1 x  x2 x  x3  .............x  x N 
=
xk  x1 xk  x2 xk  x3  .............xk  x N  i 1 x k  xi 
ik
Serhat YILMAZ, Kocaeli Üniversitesi, Elektronik
ve Haberleşme Bölümü
6
Örnek: Üçüncü dereceden bir polinomu ele alalım. Polinomun belirli
noktalarda aldığı değerler aşağıdaki gibi olsun. Bu polinomu
bulalım.
x=
P(x)=
Çözüm:
0
10
1
4
2
-8
3
-14
L1(x)=
x  1x  2x  3x  4 = x 4  10 x 3  35x 2  50 x  24
24
0  10  20  30  4
L2(x)=
x  0x  2x  3x  4 = - x 4  9 x 3  26 x 2  24 x
6
1  01  21  31  4
L3(x)=
x  0x  1x  3x  4 =
2  02  12  32  4
L4(x)=
x  0x  1x  2x  4 = - x 4  7 x 3  14 x 2  8 x
6
3  03  13  23  4
L5(x)=
x  0x  1x  2x  3 =
4  04  14  24  3
4
-2
x 4  8 x 3  19 x 2  12 x
4
x 4  6 x 3  11x 2  6 x
24
P(x)=10L1(x)+4 L2(x)-8 L3(x)-14 L4(x)-2 L5(x)
Serhat YILMAZ, Kocaeli Üniversitesi, Elektronik
ve Haberleşme Bölümü
P(x)=2x3-9x2+x+10
7
Ödev: x,y=[(0,-5), (1,-1), (2,67), (3,379), (4,1235)]
a) Noktalarından geçen polinomu Lagrange interpolasyon yöntemiyle bulun.
(P(x)=a xn+ b xn-1+….c) gibi tek polinom olacak şekilde sadeleştirin.
b) x=5 için polinomun değerini bulun. Lagrange interpolasyon yöntemiyle
yukarıda verilen noktalara ait polinomun x=5’teki değerini hesaplayan
algoritmayı oluşturun ve programını yazın.
Serhat YILMAZ, Kocaeli Üniversitesi, Elektronik
ve Haberleşme Bölümü
8
Örnek: Bir trigonometrik işlevi ele alalım. sin30o=0.5, sin450=0.7071,
sin600=0.8660 olduğu bilinmektedir. Bu durumda sin370 ve sin400
değerlerini Lagrange interpolasyon yöntemiyle bulun.
Çözüm: y1=0.5, y2=0.7071, y3=0.8660 ve x1=30, x2=45, x3=60 olduğuna göre x=37 için Lk
polinomlarını bulalım.
3
L1= 
i 1
i 1
3
L2= 
i 1
i2
3
L3= 
i 1
i 3
x  x i  x  x 2 x  x3  37  4537  60
=
=0.4088

x1  x i  x1  x 2 x1  x3  30  4530  60
x  x i  x  x1 x  x3  37  3037  60
=
=0.7155

x 2  x i  x 2  x1 x 2  x3  45  3045  60
x  x i  x  x1 x  x 2  37  3037  45
=
= -0.1244

x 3  x i  x3  x1 x3  x 2  60  3060  45
P(x)=x3+……
Buradan interpolasyon polinomu;
P(37)=L1 y1+L2 y2+L3 y3=0.4088*0.5+0.7155*0.7071-0.1244*0.8660=0.6026
Sin37’nin gerçek değeri, 0.6016’dır. Bulunan sonuç,
sadece 3 noktadan alınan örnek için iyi bir yaklaştırmadır.
Serhat YILMAZ, Kocaeli Üniversitesi, Elektronik
ve Haberleşme Bölümü
9
Şimdi aynı 3 değerden sin400’nin değerini 6 basamak duyarlılıkla bulalım.
L1=
40  4540  60 =0.222222
30  4530  60
L2=
L3=
40  3040  45 =-0.111111
60  3060  45
ve istenen değer,
40  3040  60 =0.888888
45  3045  60
P(40)=0.222222*0.5+0.888888*0.707107-0.111111*0.866025
=0.643224 olacaktır.
Bulunan sonuç, Sin400= 0.642787 değerine oldukça yakındır.
Serhat YILMAZ, Kocaeli Üniversitesi, Elektronik
ve Haberleşme Bölümü
10
Bu örneği Matlab ile sayısal olarak çözmek için şu şekilde bir program hazırlanabilir
İlk Değerleri Ata
Elimizdeki x noktaları ve bunlara karşılık gelen y değerleri, polinomun aldığı değeri
bulacağımız x noktası, Toplam=0
H
P(x)=Toplam,
k=1
k  3?
k=k+1
N
(  Lk ( x) y k )
E
k 1
Çarpım=1
E
H
i= 1
i=i+1
i  k?
E
Çarpım*( x  xi
Çarpım=
k kendisiyle
karşılaşırsa
x k  xi
Star Wars, Lucas,G., 2005
i  3?
)
H
Lk(x)=Çarpım,
N
x  xi 
)
(
i 1  x k  x i 
ik
Toplam=Toplam+L(k)*y(k)
Serhat YILMAZ, Kocaeli Üniversitesi, Elektronik
ve Haberleşme Bölümü
11
Lagrange İnterpolasyon probleminin çözümü için hazırlanan program
Serhat YILMAZ, Kocaeli Üniversitesi, Elektronik
ve Haberleşme Bölümü
12
Kaynaklar



Sayısal Çözümleme, TAPRAMAZ,R., Literatür Yayınları
Advanced Engineering Mathematics, Kreyszig,E.
Nümerik Analiz, UZUN,İ, Beta Yayınları
Serhat YILMAZ, Kocaeli Üniversitesi, Elektronik
ve Haberleşme Bölümü
13