tro
v)
.D
im
i
Meraklısına Fizik Deneme Sınavı: 16.11.2011
f.D
r.R
1. ‘Yarı Yarıya’
1.1 Hareketin yarı zamanını bir cisim v1, diğer yarısını v2 hızı ile etmektedir. Cismin ortalama
hızını bulunuz.
1(
Pr
o
1.2 Hareketin yarı yolunu bir cisim v1, diğer yarısını v2 hızı ile etmektedir. Cismin ortalama
hızını bulunuz.
1.2
01
1.3 Öz ısısı (birim kütleye düşen ısı kapasitesi) c1 ve c2, kütle miktarları bir birine eşit olan iki
sıvı karıştırılıyor. Karışımın öz ısısını (c0) bulunuz.
6.1
1.4 Öz ısısı (birim kütleye düşen ısı kapasitesi) c1 ve c2,olan iki sıvı karıştırılıyor. Bilinir ki
oluşan karışım ısıtıldığında karışımı oluşturan her bir sıvı aynı miktarda ısı içeriyor. Karışımın
öz ısısını (c0) bulunuz.
II,
1
1.5 Direnç değerleri R1 ve R2 olan iki direnç sırayla her bire Δt/2 sürede bir akım kaynağına
bağlanıyor. Δt sürede aynı kaynağa bağlı olan bir direnç açığa R1 ve R2 dirençlerin verdiği
ısıyı vermek için değeri (R) ne kadar olmalıdır?
Sı
na
vı
Not: akım kaynağı bir elektrik enerjisi kaynadır ve kaynağın dış bir devreye verdiği akım dış
devrenin direncinden bağımsızdır
me
1.6 Yukarıdaki (1.5) soruda akım kaynağa yerine gerilim kaynağı alındığında R ne kadar
olacaktır.
ne
Not: gerilim kaynağı bir elektrik enerjisi kaynadır ve kaynağın dış bir devreye verdiği gerilim
dış devrenin direncinden bağımsızdır
izi
k
De
1.7 Bir dirençten Δt/2 sürede I1, ardından yine Δt/2 sürede I2 akım geçmektedir. Δt sürede aynı
dirençte açığa toplam aynı miktarda ısı çıkması için dirençten geçek akım I0 ne kadar
olmalıdır?
lıs
ın
aF
1.8 Gerimi U1 ve U2 olan iki gerilim kaynağına sırayla aynı bir direnç bağlanıyor ve her bir
bağlanmak süresi öyle ayarlanır ki açığa ısı çıksın. Isı miktarı Q/2 olsun. Gerilimi U0 olan bir
kaynağa toplam süresi yukarıdaki direncin toplam bağlanma sürecine eşit olan bir direnci
değeri ne kadar olmalıdır ki aşığa verilen ısı miktarın değeri Q kadar olsun?
ak
2. Sızmak
IT
A
P_
FO
O:
M
er
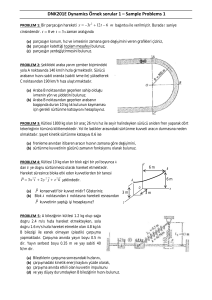
İç yarıçapı R olan bir boru içinde, uzunluğu l yarıçapı ise neredeyse R’ye eşit olan bir silindir
bulunmaktadır. Borunun duvarlı ile silindirin
yüzeyi arasındaki aralığın genişliği h’a eşittir
(h<<R) (şekildeki gibi). Bu koşula göre bu
aralıkta akın bir sıvının ortalama hızı silindirin
hızından çok daha büyüktür. Dolayısıyla silindire
etki eden sürtünme kuvvet hareketsiz silindire
etki eden sürtünme kuvvetine eşit olduğu kabul
tro
v)
.D
im
i
6.1
1.2
01
1(
Pr
o
f.D
r.R
edebilinir.
Aralıkta sıvı aktığında borunun duvarına ve silindirin yüzeyine sıvı tarafından sürtünme
kuvvetleri etki etmektedir (viskozite kuvvetleri). Bu sürtünme kuvvetin bir yüzeye düşen
değeri (hem duvara, hem de yüzeye) şu formül ile verilir:
v
f = γ ort
h
Burada vort sıvının aralıktaki ortalama hızıdır, g ise sıvının bir sabitidir ve her bir sıvı içi
değeri bilinmektedir. Aynı büyüklükte bir kuvvet sıvıya da etki etmektedir (Newton’un
3.yasasına göre). Tabii, sıvının akması için silindirlerin uçlarında bir basınç farkının
( ΔP = P0 − P1 ) oluşturması gerektir.
aF
izi
k
De
ne
me
Sı
na
vı
II,
1
A) Hareketsiz silindir
Silindir boru içinde bir iple tuttururlu olup uçlarında ΔP = P0 − P1 kadar basınç farkı
oluşturulmuştur.
2.1 Boru ile silindir arasındaki akan sıvının ortalama hızını (vort) bulunuz.
2.2 Sıvı akısını (birim zamanda geçen sıvı hacmi) bulunuz.
2.3 İpin gerilme kuvvetin değerini bulunuz. Neden ve ne kadar bu kuvvet basınç farkından
oluşan kuvvetten farklıdır?
er
ak
lıs
ın
B) ‘Batmak ve kaldırmak’
Boru ve silindir dikey durumda, borunun üst ucu açık, alt ucu ise kapalıdır ve boru yoğunlu
ρ0 olan bir sıvı ile tamamen doludur (şekildeki gibi). Silindiri oluşturan maddenin yoğunlu ρ1
dir (ρ1>ρ0).
2.4 Silindir u sabit hızı ile alçalıyor. Buna göre boru ile silindirin aralığında akan sıvını
ortalama hızı ne kadardır?
FO
O:
M
2.5 Silindirin alt ve üst uçları arasındaki basınç farkını ( ΔP = P0 − P1 ) bulunuz. Neden ve ne
IT
A
P_
kadar bu basınç farkı aralıktaki sıvının hidrostatik basıncından farklıdır?
2.6 Silindirin batma hızı (u) ne kadardır?
Batırtılmış silindirin kaldırması: silindirin yoğunluğu sıvının yoğunluğundan daha düşük
olsun (ρ1<ρ0).
tro
v)
.D
im
i
2.7 Bu durumda silindirin alt ve üst uçları arasındaki basınç farkını ( ΔP = P0 − P1 ) bulunuz.
f.D
r.R
2.8 Silindirin kaldırma hızı (u) ne kadardır?
3. Ağ devreleri
1.2
01
1(
Pr
o
3.1 Şekildeki verilen devrede dirençlerin değerleri R1 = 1.0Ω, R2 = 2.0Ω, R3 = 4.0Ω, R4 = 1.0Ω ,
R1 geçen akım ise I1 = 1.0 A dir. Bu verilere göre
bulunuz:
a)dirençlerden
geçen
akımları;
b)dirençlerdeki gerilimleri; c)AD uçları arasındaki
gerilimi; a)devrenin eşdeğer direncini.
me
Sı
na
vı
II,
1
6.1
3.2 Direnci R0 olan özdeş çubuklardan şekildeki gibi bir desen yapılmıştır. Bu desen direnci
ihmal edebilinecek kadar düşük olan ABCD iletken çerçeveye tutturulmaktadır. Desenin
merkez noktası ile çerçeve arasında bir elektrik akım
kaynağı bağlanıyor ve toplam akımın değeri I0 kadardır. A
ve O noktaları arasındaki gerilimi bulunuz.
ak
lıs
ın
aF
izi
k
De
ne
3.1 Birim uzunluğun direnci r olan bir telden şekildeki gibi bir desen oluşturulmuştur.
şekilde
Desenin
geometrik
boyutları
(a,b)
gösterilmiştir. Ağının tüm sol uçları direnci ihmal
edilen AB çubuğuna bağlıdır. Çubuk ve ağının sol ucu
(O) bir elektrik kaynağına bağlıdır ve toplam akının
değeri I0 dır. A ve O noktaları arasındaki gerilimi ve
eşdeğer direnci bulunuz.
er
4. Çivi
FO
O:
M
Bu soruda bir çivinin çakmaklığında yer alan fiziksel olaylar incelemektedir. Sorunun 1
kısmında çivi ile çekiç arasındaki etkileşme, 2. kısmında ise çiviye vurduktan sonra çivinin
tahtada hareketi incelenmektedir.
IT
A
P_
A)Çivi ile çekicin çarpışması
tro
v)
.D
im
i
1(
Pr
o
f.D
r.R
Kütlesi M hızı ise v0 olan bir çekiç kütlesi m olan bir çiviye çarpmaktadır. Çekiç ile çivi
arasındaki etkileşme süre çok düşük, çarpışma ise esnektir.
m
4.1 Çarpışmadan hemen sonra çivinin hızını (u) bulunuz. Bu hızı v0 ve γ =
sayısını
M
kullanarak yazınız.
4.2 Eğer γ 1 çivinin hızı ne kadardır?
4.3 Çivinin kinetik enerjisin değeri çarpışmanın hemen ardından ve çekicin kinetik enerjisinin
çarpışmadan bir an önce değeri ile oranı (η) ne kadardır? Bu değeri γ sabitini kullanarak
yazınız.
1.2
01
B)Çivinin tahtada hareketi
II,
1
6.1
Çivi tahtada hareket ederken sürtünme kuvveti yer çekim kuvvetin çok daha büyük olduğuna
göre yer çekim kuvveti ihmal edilir. Tabii ki sürtünme kuvvet sadece
çivin tahta içinde bulunan yüzeyine etki etmektedir ve çivinin sivri
ucuna etki eden sürtünme ile çivinin yan yüzeyine sürtünme
kuvvetlerin doğasında bir fark bulunmalıdır. Çivinin yan yüzeyine
etki eden sürtünme kuvvet yüzeyin alanına orantılıdır, dolayısıyla
çivinin tahtaya giren kısmın uzunluğuna da orantılıdır (şekildeki
gibi), yani Fyan = kx , burada k bilinen bir sabit (ilerdeki hesaplarda
Sı
na
vı
onu varsayınız), x ise çivinin tahta içindeki uzunluğu dur. Diğer elde,
tahtayı homojen olarak kabul edersek, çivinin sivri ucuna etki eden
sürtünme kuvvet ( Fuç = f ) bir sabit olmalıdır ve ilerde onu da
De
ne
me
varsayınız. Çivi çarpışmadan önce tahtanın içine x kadar girdiğini
kabul edelim (çivinin sivri ucunun uzunluğunu ihmal ediniz). Çekiçle
E
çarpışmadan sonra çivi kadar kinetik enerji kazandığını ve bu enerjiyi kullanıp tahta içine
Δx kadar içeri girdiğini kabul edelim.
4.4 Δx’i ilk parametrelerin (E,x,k ve f) bir ifadesi olarak bulunuz.
4.5 Uzunluğu l olan bir çiviyi bir çarpmakla tamamen tahtaya sokmak için çiviye aktarılan
enerji (E1) ne kadar olmalıdır? Sınır durumlarını inceleyiniz ne zaman sürtünme kuvvetlerden
biri diğerinden çok daha büyüktür.
4.6 Fyan Fuç ve her bir çarpışmada çiviye verilen kinetik enerji miktarı E kadar olduğunu
aF
izi
k
kabul edelim. Bu durumda çiviyi tahta içine tamamen çakmak için çekiç ile çiviye kaç kez
(N1) vurmamız gerekecektir?
4.7 Fyan Fuç ve her bir çarpışmada çiviye verilen kinetik enerji miktarı yine E kadar
lıs
ın
olduğunu kabul edelim.. Bu durum için xn2+1 = xn2 + ε doğru olduğunu ispatlayınız, burada ε
bir sabittir ve bu sabiti E ve k parametrelerin bir ifadesi olarak bulunuz. Ayrıca, bu durumda
çiviyi tahta içine tamamen çakmak için çekiç ile çiviye kaç kez (N2) vurmamız gerekecektir?
er
ak
5. Su ve buhar
Suyun bazı özelliklerini hatırlattıralım:
FO
O:
M
kg
kg
, yoğunluğu ρ = 103 3 (sıcaklıkla değişmediğini
mol
m
kJ
kabul ediniz), öz ısısı sabit ve c0 = 4.2
’e eşittir.
kg ⋅ K
IT
A
P_
Suyun moleküler kütlesi M = 18 ⋅10−3
tro
v)
.D
im
i
Buharlaşma ısısı aslında sıcaklığa bağlıdır ama soruda onu yaklaşık sabit ve L = 2.3 ⋅106
J
,
mol ⋅ K
f.D
r.R
eşit olduğunu kabul ediniz.
J
’e
kg
Su buharın mol ısı kapasitesi cV = 3R ’ye eşittir, burada gaz sabiti R = 8.31
J
, açık hava basıncı p0 = 1⋅105 Pa ve mutlak sıfır
K
0
sıcaklığı t0 = −273.15 C olarak alınız.
Doymuş buharın kısmi basıncını sıcaklığın fonksiyonu olarak tabloda verilmiştir.
5
0.87
50
12.3
10
1.22
60
19.9
15
1.70
70
31.0
20
2.33
80
47.3
25
3.15
90
70.0
30
35
4.23 5.60
100
101
1.2
01
0
0.61
40
7.35
6.1
t0C
P(kPa)
t0 C
P(kPa)
1(
Pr
o
Boltzmann’ın sabiti k = 1.38 ⋅10−23
me
Sı
na
vı
II,
1
5.1 Dış basınç p = 1.27 ⋅105 Pa iken suyun buharlaşma sıcaklığını bulunuz.
5.2 Hacmi V = 10m3 olan bir kapta t = 700 C sıcaklıkta doymuş buhar bulunmaktadır. Bu
buharın kütlesi ne kadardır?
5.3 Üst ucu kapalı, alt ucu ise açık olan dikey bir silindirik kapta t = 800 C sıcaklıkta bilinen
bir miktarda su bulunmaktadır ve suyun üst yüzeyi kabın üst ucundadır. Bu su sütunu
mekanik dengede olduğuna göre uzunluğu ne kadar olmalıdır?
5.4 Su buharın (sabit hacimde) ve suyun sıvı durumdaki öz ısıların oranını bulunuz.
5.5 t0 = 200 C sıcaklıkta ve açık havada bulunan su buhar haline getirmelidir. Bu olay için
gereken ısının kaçta kaçı suyun buharlaşma sıcaklına kadar ısıtmaya harcanacaktır?
5.6 Hacmi V = 1.0m3 olan yalıtılmış bir kapta t0 = 1400 C sıcaklıkta doymuş buhar
ne
bulunmaktadır. Sıcaklığı t1 = 100 C miktarı ise m1 = 10 g olan soğuk su buharın içine
püskürtülüyor. Kapta termodinamik denge oluştuğunda sıcaklık ne kadar olacaktır?
De
6. EMK
izi
k
Bu soruda bir DC devresinde yer alan olaylar incelenmektedir.
IT
A
P_
FO
O:
M
er
ak
lıs
ın
aF
6.1 İç direnci r, gerilimi ε olan bir emk’ın uçlarına değeri R değişken olan bir direnç bağlıdır
(şekildeki gibi). Uygun akım birimi kullanarak (ilerdeki sorularda da birimler
Sİ birimlerden farklı olabilir, yetir ki onlar daha uygun olsun) verilen
koordinat sisteminde akımın R direncin fonksiyonun ( I = I ( R) )grafiğini
çiziniz.
tro
v)
.D
im
i
f.D
r.R
Pr
o
1(
1.2
01
II,
1
6.1
6.2 Benzer koordinat sistemde gerilimin R direncin fonksiyonun ( U = U ( R) )grafiğini çiziniz.
6.3 Benzer koordinat sistemde R dirençte açığa çıkan gücünün R direncin fonksiyonun
( P = P( R) )grafiğini çiziniz.
6.4 Benzer koordinat sistemde devrenin veriminin R direncin fonksiyonun
(η = η ( R) )grafiğini çiziniz.
vı
Pratikte gereken güce ulaşmak için bilinen sayıda olan elektik kaynakları farklı şekillerde
bağlanabilir.
ne
me
Sı
na
6.5 Her birinin gerilimi ε, iç direncinin değeri ise r olan N tane emk seri olarak bağlıdır ve bu
emk sistemin uçlarına değeri R olan bir direnç bağlıdır (şekildeki
gibi). Dış dirençteki gücü (P(R))bulunuz.
lıs
ın
aF
izi
k
De
6.6 Her birinin gerilimi ε, iç direncinin değeri ise r olan N tane emk paralel olarak bağlıdır ve
bu emk sistemin uçlarına değeri R olan bir direnç bağlıdır (şekildeki
gibi). Dış dirençteki gücü (P(R))bulunuz.
ak
Genel olarak piller özdeş olmak zorunda değildir ama özdeş olması pratik açısından daha
uygundur.
IT
A
P_
FO
O:
M
er
6.7 Siz pillerin özdeş olmasına dik etmemişsiniz ve gerilimleri ve iç dirençleri sırasıyla e1, r1
ve e2, r2 olan iki pil almışsınız. Piller paralel olarak bağlandığında
(şekildeki gibi) dış dirençteki gücü (P(R)) bulunuz.
tro
v)
.D
im
i
1(
Pr
o
f.D
r.R
6.8 Yine dikkatsizlikten pillerin kutuplarını bağlarken onlarını karıştırmışsınız (şekildeki
gibi). Dış dirençteki gücün sıfır olması için (P(R)=0) pillerin gerilimleri
ve iç dirençleri arasında nasıl bağlantı olmalıdır?
1.2
01
7. Yarı çember
Size bu soruda titreşim ve katı cisimlerin hareketinin bazı formülleri lazım olacaktır...
vı
II,
1
6.1
A)Yay sabiti k, bir ucu bir dikey duvara, diğer ucuna ise kütlesi m olan bir cisim bağlı olan
yay sistemine yatay düzlemde hareket ettiğinde yatay
sarkaç sistemi denir (şekildeki gibi). İlk anda cisim
denge durumdan bilinen bir x0 mesafeye kadar
saptırılmıştır.
me
Sı
na
7.1 Sürtünmeyi ihmal ederek yayın ucundaki cismin mekanik enerjisinin koruma yasasına
yazınız.
7.2 Bulunan enerji koruma yasasını v 2 + ω02 x 2 = sabit şekiline getirip titreşimin periyotunun
formülünü bulunuz. Burada v cismin hızı, ω0 bir sabit, x ise cismin denge durumundan
sapması.
aF
izi
k
De
ne
B)Uzunluğu l olan ve tavana asılan hafif kütleli bir ipin ucuna asılan bir cismin oluşturduğu
sisteme (şekildeki gibi) matematiksel sarkaç denir. İpin dikeyle
yapığı açıyı (α) sarkacın konumu olarak alınız.
lıs
ın
7.3 Sürtünmeyi ihmal ederek ve α açısını cismin koordinatı olarak kullanıp cisim için enerji
koruma yasasına yazınız.
er
ak
7.4 α 1 kabul ederek bulunan enerji koruma yasasını v 2 + ω02l 2α 2 = sabit şekiline getirip
titreşimin periyotunun formülünü bulunuz. Burada v cismin hızı, ω0 ise bir sabittir.
FO
O:
M
C) Yarı çemberin titreşimi
IT
A
P_
Katı bir cismin genel hareketini incelerken cisim bir noktasal cisim olarak kabul edilemez ve
katı cismin mekanik enerjisinin ifadesi noktasal bir cisminin enerji
ifadesinden çok daha karışık olabilir.
tro
v)
.D
im
i
7.5 Yer çekim alanında bulunan bir katı cismin potansiyel enerjisi E p = mghC ’ye eşit odlunu
f.D
r.R
ispatlayınız. Burada m cismin kütlesi, hC zeminden yüksekilği, g ise yer çekim ivmesidir
(şekildeki gibi).
1.2
01
1(
Pr
o
Yarıçapı R olan ince duvarlı bir borudan yarı çember kesiliyor. Çemberin uçları ince, hafif
kütleli bir AB teliyle bağlanıyor (şekildeki gibi). Telin
bükülmesini ihmal ediniz.
7.6 Yarı çemberin kütle merkezi (C) çemberin merkezinden (O) hC =
2
π
R uzaklıkta
Sı
na
vı
II,
1
6.1
bulunduğunu gösteriniz.
7.7 Yarı çember çemberin merkezinden (O) geçen yatay bir eksene asıldığında (şekildeki gibi)
çemberin küçük titreşim periyotunu bulunuz.
ne
me
7.8 Yarı çember çemberin tepe noktasından (A) geçen yatay bir eksene asıldığında (şekildeki
gibi) çemberin küçük titreşim periyotunu bulunuz.
lıs
ın
aF
izi
k
De
7.9 Yarı çember pürüzlü yatay bir düzlemde şekildeki gibi yerleştiriliyor ve bir hafif itme ile
dengeden çıkarılıyor. Yarı çember düzlemde kaymadan küçük yuvarlanma yapmaktadır. Bu
titreşimin periyotunu bulunuz.
ak
8. Elektrik dreyfi
FO
O:
M
er
Bu soruda yüklü bir cismin bir birine dik olan elektrik ve manyetik alanında hareketi
incelenmektedir.
A) Yükü q>0, kütlesi ise m olan bir cisim şiddeti B olan homojen bir manyetik alanın
bölgesine, alana dik olarak v0 hızı ile girmektedir.(Bu örnekte elektrik alını yoktur)
IT
A
P_
8.1 Cismin hareket ettiği çemberin yarıçapını bulunuz.
tro
v)
.D
im
i
8.2 Dönmenin açısal hızını (ω) bulunuz
8.3 Cismin çemberde dönme periyotunu (T) bulunuz
1.2
01
1(
Pr
o
f.D
r.R
B)Uzayın bilinen bir bölgesinde B manyetik alanla birlikte, manyetik alan dik olarak E
elektrik alanı da bulunmaktadır. Pozitif yükü q, kütlesi ise m olan bir cisim bilinen bir hız ile
bu bölgeye girmektedir. Cismin hızı manyetik alanı dik
olan bir düzlemde bulunmaktadır (şekildeki gibi).
Bölgede elektrik alanın bulunması cismin hızının
elektrik alanın çizgileri boyunca büyümesine sebep
olmaktadır. Dolayısıyla cismin yörüngesinin eğrilik
yarıçapı da büyüyecektir. Sonuç olarak, cisim yavaş,
yavaş OX ekseni boyunca kayacaktır ve yörüngesi
şekildekine benzeyecektir.
Sı
na
vı
II,
1
6.1
8.4 Yaklaşık çözüm: burada cismin kayma hızını yaklaşık bir şekilde hesaplanmaktadır.
Cismin yörüngesinin iki, üst ve alt yarı çemberden oluştuğunu
kabul edelim (şekildeki gibi). Üst yarı çemberde cismin hızı sabit
olarak tepe noktasındaki hızına (vu), alt yarı çemberde ise çukur
noktadaki hızına (va) eşit olsun. Bu yaklaşık modele göre cismin
OX eksen boyunca ortalama kayma hızını (vD) bulunuz.
aF
izi
k
De
ne
me
C)Tam çözüm
8.5 Cisim bir birine dik olan E ve B elektromanyetik alanında hareket etmektedir (şekildeki
gibi). Cismin hızının izdüşümleri vx ve vy dir. Cismin ivmesinin izdüşümleri için ifade
yazınız.
FO
O:
M
er
ak
lıs
ın
Yarıçapı R, dingilin yarıçapı ise r olan bir çember kaymadan OX eksen boyunca u hızı ile
IT
A
P_
yuvarlanmaktadır (şekildeki gibi).
tro
v)
.D
im
i
IT
A
P_
FO
O:
M
er
ak
lıs
ın
aF
izi
k
De
ne
me
Sı
na
vı
II,
1
6.1
1.2
01
1(
Pr
o
f.D
r.R
8.6 Açısal konumu OX eksene göre ϕ olan A noktasının hızının izdüşümleri için ifade
yazınız.
8.7 A noktasının ivmesinin izdüşümleri için ifade yazınız ve hızının izdüşümleriyle
bağlantıları bulunuz.
8.8 Elektromanyetik alanda hareket eden cismin denklemleriyle benzerliği kullanıp kayma
hızının tam çözümünü bulunuz.