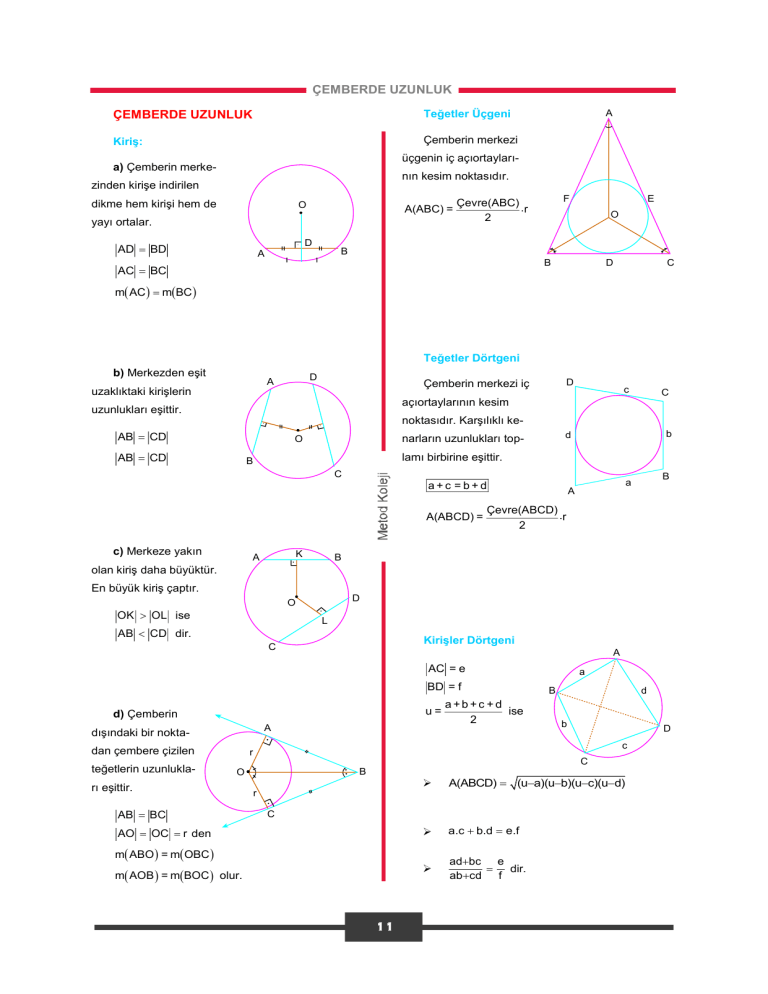
ÇEMBERDE UZUNLUK ÇEMBERDE UZUNLUK Teğetler Üçgeni Kiriş: Çemberin merkezi A üçgenin iç açıortayları- a) Çemberin merke- nın kesim noktasıdır. zinden kirişe indirilen dikme hem kirişi hem de O A(ABC) = yayı ortalar. F Çevre(ABC) .r 2 E O D AD BD B A B AC BC D C m AC mBC Teğetler Dörtgeni b) Merkezden eşit D A uzaklıktaki kirişlerin Çemberin merkezi iç D c C açıortaylarının kesim uzunlukları eşittir. noktasıdır. Karşılıklı ke- AB CD AB CD b d narların uzunlukları top- O lamı birbirine eşittir. B C A(ABCD) = c) Merkeze yakın K A B a a+c = b+d A Çevre(ABCD) .r 2 B olan kiriş daha büyüktür. En büyük kiriş çaptır. D O OK OL ise L AB CD dir. Kirişler Dörtgeni C A AC = e BD = f a+b+c +d u= ise 2 d) Çemberin A dışındaki bir noktadan çembere çizilen teğetlerin uzunlukla- a d B b D c r C B O rı eşittir. AB BC A(ABCD) (ua)(ub)(uc)(ud) a.c b.d e.f adbc e dir. ab cd f r C AO OC r den m ABO = m OBC m AOB = mBOC olur. 11 ÇEMBERDE UZUNLUK İki Çemberin Birbirine Göre Durumu: Çemberler içten teğet ise; Çemberler ayrık ise; r1 r2 C r1 C A B O1 D O1 O2 r2 D O2 O1 O2 r1 r2 r1 r2 < O1 O2 İki Çemberin Ortak Teğetleri: AB O1 O2 (r1 r2 ) İki çemberin ortak teğetlerinin uzunlukları CD O1 O2 (r1 r2 ) eşittir. Çemberler dıştan teğet ise; AB CD m(BKD) m(ALC) C r1 r1 r2 r2 O2 O1 D A B r1 r2 O1 O2 CD 2(r1 r2 ) L K Çemberler iki noktada kesişiyorsa; C C r1 a O1 r2 A b B cO D 2 D A(CED) 90 EK CK KD A O1B a b O2A b c B O1 O2 a b c E r1 r2 O1 O2 r1 r2 Çemberler dik kesişiyorsa; C A r1 K D AC BD r2 O2 O1 A D O1A r12 2 O2 A r2 O1 O2 2 B 12 12 C ÇEMBERDE UZUNLUK Örnek 42 AB DC B A Şekildeki çembere, B AB CD E 6 C A D AE 2 cm O E BE 6 cm 2 ED 3 CE D C Buna göre, ED kaç cm dir? Teğetlerin değme noktasından geçen ve herhangi bir d doğrusuna dik olan doğrular iki çemberinde merkezinden geçer. d d Örnek 43 K L K A L B, C, D, E çember 9 üzerinde x B AB 9 cm D 16 1. AD x 2x O A BC 16 cm DE 2x C C E E Yukarıdaki verilere göre, AD x kaç cm dir? B D AE . BE CE . DE Örnek 44 B 2 A D 3 B P E C 12 [AD ve [AC A çembere D ve C noktalarında teğet BC AD DB 3 cm D PA . PB PC . PD C AB 12 cm 3. Yukarıdaki verilere göre, EC kaç cm dir? A B P C 2 AP BP . CP 13 13 ÇEMBERDE UZUNLUK Örnek 45 Örnek 48 Şekildeki çemberde B E 6 x 1 O çemberin merkezi B A, C, B doğrusal 15 teğet, AC 7 cm O OC 15 cm AC 4 cm K C 25 7 C AB 6 cm A 4 A [AB, B noktasında 3 D L BC 25 cm KD 3 cm LK 1 cm Yukarıdaki verilere göre, O merkezli çemberin en KE x uzun kirişi kaç cm dir? Yukarıdaki verilere göre, x kaç cm dir? Örnek 49 Örnek 46 A Şekilde d doğrusu K çemberlere, A ve D B noktalarında O E teğettir. M ve O M 12 A B merkezli çember- d lerin yarıçapları sırasıyla 2 cm ve 9 B 16 cm dir. C ABC dik üçgen m(ABC) 90, A ve C merkezli, B AB 24 cm olduğuna göre, çemberler arasındaki noktasından geçen çember yayları K noktasında kesişiyor. en kısa uzaklık kaç cm dir? AB 15 cm, BC 16 cm olduğuna göre, K noktasının [AC] ye olan uzaklığı kaç cm dir? Örnek 50 Şekilde AB; çembere Örnek 47 A O, çemberin merkezi D A AB 16 cm B AB DC 24 cm O C B teğettir. 16 AB OE DC OF F E A ve B noktalarında OE 4x 3 Çemberlerin yarıçapları toplamı 12 cm ise çemberler OF 2x 3 arasındaki uzaklık kaç cm dir? Yukarıdaki verilere göre, çemberin yarıçapı kaç cm dir? 14 14 ÇEMBERDE UZUNLUK Örnek 51 Örnek 54 d D d doğrusu, A C ve B merkezli D A 11 E [EC], K noktasında O 10 çemberlere C 5 F Şekilde, merkezli yarım ve D B 2 noktalarında K çembere teğettir. E EK 2 cm teğettir. C KC 10 cm AE 11 cm A O B BF 5 cm ABCD dikdörtgen olduğuna göre, çemberin yarıçapı DC 12 cm kaç cm dir? Yukarıdaki verilere göre, EF kaç cm dir? Örnek 55 Örnek 52 A O merkezli çemberde A [CD], D noktasında B 2 C 4 AC 12 cm 10 teğet O ABC bir üçgen D B AC CD 12 8 BD 10 cm BE 9 cm 9 E BC 2 cm C DE 8 cm CD 4 cm D Yukarıdaki verilere göre, AD kaç cm dir? Yukarıdaki verilere göre, çemberin yarıçapı kaç cm dir? Örnek 53 Örnek 56 Şekildeki A, B, C A Şekildeki çemberde merkezli üç çember m(DAC) m(BCD) ikişer ikişer birbirine A 12 teğet ve merkezleri B C AC 8 cm 8 BC 10 cm ABC üçgeninin köşeleridir. B Çemberlerin yarıçapları sırasıyla 8 cm, 3 cm, 2 cm olduğuna göre, üçgenin çevresi kaç cm dir? E C AB 12 cm D Yukarıdaki verilere göre, DE kaç cm dir? 15 15 ÇEMBERDE UZUNLUK Örnek 57 Örnek 60 E D O çemberin merkezi F C D A B E m(EAC) 30 30o C O CK 2 cm K noktasında teğet 6 ABCD dik yamuk 2 [AE] çembere D KB 8 cm O 8 DC 6 cm A L B Şekildeki ABCD dik yamuğunun kenarları O merkezli Yukarıdaki verilere göre, AB kaç cm dir? çembere E, F, K ve L noktalarında teğet ise çemberin yarıçapı kaç cm dir? Örnek 58 Örnek 61 ABC bir dik üçgen A A O iç teğet D ABCD dikdörtgen DK KC çemberin merkezi E D F 12 AB AC L K AF 12 cm BF 4 cm O FC 5 cm B 4 F 5 B C E C Yukarıdaki şekilde E merkezli yarım çember ile D Yukarıdaki verilere göre, Alan(ABC) kaç cm2 dir? merkezli çember L noktasında teğet olduğuna göre, Alan(ABCD) kaç cm2 dir? Örnek 59 B O merkezli çeyrek Örnek 62 çember O1 merkezli F çembere C C m(AEB) m(DFC) 180 AB 6 cm noktasında [BO], K K O1 noktasında [OA], L D 12 noktasında teğettir. O L C DC 12 cm A A 6 O merkezli çeyrek çemberin yarıçapı 6 cm ise OL E kaç cm dir? B Yukarıdaki verilere göre, çemberin çapı kaç cm dir? 16 16 ÇEMBERDE UZUNLUK Örnek 63 Örnek 66 A 9 E y O merkezli D A çember yayı C C ve E 8 noktasından T geçiyor. ABCD O 6 C dikdörtgen B OB 6 cm 60o O DC 8 cm 1 x B Koordinat eksenlerine teğet olan A merkezli çember, [BC] ye T noktasında teğet, m(OBC) 60 AE 9 cm Yukarıdaki verilere göre, ED kaç cm dir? OB 1 cm olduğuna göre, çemberin yarıçapı kaç cm dir? Örnek 67 Örnek 64 Yarıçapları 4 cm olan F D A O, merkezli altı eş çember çember yayı E, A, birbirine şekildeki gibi F noktalarından teğettir. geçiyor. ABCD kare Yukarıdaki çemberlerin etrafına sarılan ipin uzunluğu EB 1 cm E 1 B C 7 O en az kaç cm dir? OC 7 cm Yukarıdaki verilere göre, karenin alanı kaç cm2 dir? Örnek 68 A merkezi Örnek 65 A O, çeyrek çemberin OA OB 8 2 D C ABCD kare, [DC], O BC 7 cm merkezli çembere E O E AC 8 2 cm 7 noktasından teğet Çevre(ABCD) = 16 cm O B Yukarıdaki verilere göre, çemberin yarıçapı kaç cm B C Yukarıdaki verilere göre, çemberin yarıçapı kaç cm dir? dir? 17 17