Slayt 1 - sincan ali semerkandi imam hatip ortaokulu

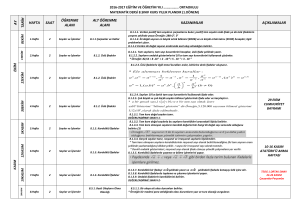
8 cm
- 8 cm
8 cm - 8 cm
Alanı 64 cm2 olan kare şeklindeki bir panonun bir kenarının
uzunluğunu bulalım.
• Verilen bir sayının, hangi sayının karesi olduğunu bulma
işlemine karekök alma denir.
•
Karekök
sembolü ile gösterilir.
• Kareköklü sayılar okunurken;( karekök+verilen sayı) diye
okunur.
•
Bir sayının karekökü her zaman pozitiftir.
Okunuşu
ÖRNEK
7
Okunuşu
64
Karekök yedi
Karekök atmış dört
Karekökleri tam sayı olan doğal sayılara tam
kare doğal sayılar denir.
0,1 , 4
ÖRNEK
,
9 , 16
,
25 , 36
,
…
Aşağıdaki sayılardan hangisi tam kare değildir?
121
= 11
196
225
169
= 13
= 15
624
= 14
Tam kare olmayan sayıların karekökleri tahmin edilirken,
1. Verilen sayıdan küçük en büyük tam kare yazılır.
2. Verilen sayıdan büyük en küçük tam kare yazılır.
3. Elde edilen sayıların karekökü alınır.
ÖRNEK
98
Sayısının sonucunu yaklaşık olarak tahmin edelim.
81 < 98 < 100
81 < 98 <
100
9 < 98 < 10
İki tam sayının oranı şeklinde yazılamayan sayılara irrasyonel
sayılar denir. İrrasyonel sayılar ‘I’ harfi ile gösterilir.
İrrasyonel sayıların ondalık kısmındaki sayılar düzensiz olarak
sonsuza kadar ilerler. Bundan dolayı irrasyonel sayılar iki tam
sayının oranı biçiminde yazılamazlar. İrrasyonel sayıların diğer
adı da kareköklü sayılardır.
ÖRNEK
Aşağıdaki sayılardan hangisi irrasyonel sayıdır?
0,1
12,2
0,3765490456…
0,1212121212…
ÇERÇEK SAYILAR
Q: RASYONEL SAYILAR
5
Z: TAM SAYILAR
I : İRRASYONEL SAYILAR
N: DOĞAL SAYILAR
2
17
8
Rasyonel ve irrasyonel sayı kümelerinin birleşimi olan kümeye
gerçek sayılar kümesi denir. Gerçek sayılar kümesi R harfi ile
gösterilir. Gerçek sayılar sayı doğrusunu tamamen doldurulur.
Tam kare olmayan sayıların karekökü bulunurken;
1. Sayı içinde tam kare olacak şekilde parçalanır.
2. Tam kare kökün dışına çıkarılır.
3. Kalan sayılar kökün içinde bırakılır.
ÖRNEK
Aşağıda verilen sayıların karekökünü bulunuz.
98 =
49.2 = 7
2
Bu gösterime
a
gösterimi denir.
27
=
9.3
= 3
3
b
a
b
biçiminde verilen bir kareköklü sayının kat sayısı
kök içine atılırken karesi alınarak kök içine alınır ve kök
içindeki sayı ile çarpılır..
a
ÖRNEK
b
=
a2 . b
Aşağıda verilen kareköklü sayıların katsayılarını
kök içine alınız.
5
2
=
52 . 2 =
25 . 2 =
50
4
6
=
42 . 6 =
16 . 6 =
96
Kareköklü sayılarla toplama veya çıkarma işlemleri yapılırken;
1. Kareköklerin içindeki sayılar eşit ise katsayılar toplanır
ve ortak kök aynen yazılır..
a
x
+
b
x
=
a
+
b
x
a
x
-
b
x
=
a
-
b
x
2.Kareköklerin içindeki sayılar eşit değil ise eşitlenmeye
çalışılır. Eşitlenebiliyorsa toplama veya çıkarma işlemleri
yapılır. Eşitlenemiyorsa toplama veya çıkarma işlemleri
yapılamaz.
ÖRNEK
3
5
+
4
5
İşleminin sonucunu bulunuz.
3
5
+
4
5
=
=
3
7
+
5
4
5
ÖRNEK
9
6
-
5
6
İşleminin sonucunu bulunuz.
9
6
-
5
6
=
=
9
4
-
6
5
6
ÖRNEK
27 -
48 +
75
İşleminin sonucunu bulunuz.
3
27 =
9.3
= 3
3
48 =
16.3 = 4
3
75 =
25.3 = 5
3
3 - 4
3 + 5
3
=
3–4+5
= 4
3
3
Kareköklü sayılarla çarpma işlemi yapılırken;
1. Katsayılar çarpılır.
2. Kök içindeki sayılar aynı kök içerisine alınarak çarpılır.
3. Kök içindeki sayı içerisindeki tam kareler dışarı atılır.
a
x
.
b
y
=
a
.
b
x
.
y
ÖRNEK
2
3
.
5
6
İşleminin sonucunu bulunuz.
2
3
.
5
6
=
2
=
10
18
=
10
9.2
=
10.3
=
30
.
5
2
2
3
.
6
2
2 m
ÖRNEK
3
5 m
Yukarıda kenar uzunlukları verilen kalının alanını bulunuz.
2
2
.
3
5
=
=
2
6
.
3
10
2
m2
.
5
Kareköklü sayılarla bölme işlemi yapılırken;
1. Katsayılar bölünür.
2. Kök içindeki sayılar aynı kök içerisine alınarak bölünür.
3. Kök içindeki sayı içerisindeki tam kareler dışarı atılır.
a
x
:
b
y
=
a
:
b
x
:
y
ÖRNEK
4
32
:
2
8
İşleminin sonucunu bulunuz.
4
32
:
2
8
=
4
=
2
=
2
=
4
:
4
.
2
2
32
:
8
ÖRNEK
15
50 m²
3
5 m
Yukarıda alanı ve bir kenar uzunluğu verilen bir havuzun diğer
kenar uzunluğunu bulunuz.
15
50 : 3
15
5 =
=
5
:
3
10
50
:
5
Kareköklü sayılarla sıralama işlemi yapılırken; kat sayılar
kök içine alınır. Kök içine alındıktan sonra kök içi büyük olan
kareköklü sayı daha büyüktür.
a
b
=
a2 . b
2
5
3 10
ÖRNEK
4
6
Yukarıda verilen kareköklü sayıları küçükten büyüğe sıralayınız.
2² . 5
2
5
3
10 =
4
6
=
2
5
=
=
20
3² . 10 =
9 . 10 =
90
4² . 6
16 . 6
96
< 3
=
=
4 .5
10 < 4
6
=
Ondalık sayıların karekökü alınırken;
1. Ondalık sayı rasyonel yapılır.
2. Payın karekökü alınır.
3. Paydanın karekökü alınır.
4. Varsa sadeleştirme yapılır.
0,25
ÖRNEK
Yukarıda verilen sayının karekökünü bulunuz.
25
0,25 =
25
=
100
5
=
100
1
=
10
2
ÖRNEK
1,44 +
0,09
İşleminin sonucunu bulunuz.
144
1,44 =
0,09 =
144
=
12
=
100
100
10
9
9
3
=
100
12
10
=
100
+
3
10
=
10
15
10
= 1,5
Sorularda kökler iç içe verilirse işlem en içteki kökten
dışa doğru yapılır.
ÖRNEK
86 -
14 +
121
İşleminin sonucunu bulunuz.
86 -
14 +
121 =
=
86 -
14 + 11 =
86 - 5 =
81 =
86 9
25