Nicel Analizlere Giri

Nicel Analizlere Giriş
Yrd. Doç. Dr. İhsan Sarı
Veri toplama işlemi ile birlikte toplanan veriler
HAM VERİ olarak adlandırılır.
Veri analizi yöntemi ile ham veriye anlam
kazandırılır.
BAZI KONTROLLER YAPILMALIDIR
Ölçme: önceden belirlenmiş olan kurallara göre,
nesnelere ve objelere sayılar atfetme.
Ölçeme de hata: ölçülmek istenen gerçek
değerden sapmalardır.
SOSYAL BİLİMLERDE HER ÖLÇÜMDE BELLİ
DÜZEYDE HATA MEVCUTTUR.
GERÇEK DEĞER = ÖLÇÜLEN DEĞER + HATALAR
Hata kaynakları
•
•
•
•
•
Deneğin karakteri
Kısa süreli kişisel faktörler (sağlık, duygu vb.)
Örnekleme ve ölçeklerden kaynaklı hatalar
Durumsal faktörler
Mekanik faktörler (silik yazı veya sıkışık
hazırlanmış sorular)
• Anketin uygulanması ile ilgili faktörler (örn:
mülakatçı yönlendirmesi)
• Analizle ilgili faktörler
En genel halde ölçme hatalarının
sınıflandırılması
• Sistematik hatalar
• Tesadüfi hatalar
Saha çalışması kaynaklı hatalar
• Örnekleme hataları
• Örnekleme dışı hatalar
Veri hazırlama süreci
Saha çalışmasında elde edilen ham verilerin
analize hazır hale getirilmesi amacıyla yapılan
işlemler dizisidir.
Amaç: ham verinin yapısında olan ve sıhhatini
bozan hatalar ve sorunların ortadan kaldırılması.
Veri hazırlama süreci basamakları
1.
2.
3.
4.
5.
6.
7.
Anketlerin kontrol edilmesi
Düzenleme (edit etme)
Kodlama
Verinin bilgisayar ortamına aktarılması
Veri temizleme
İstatistiksel düzenlemeler
Uygun analiz stratejisinin seçilmesi
Anketlerin kontrol edilmesi
•
•
•
•
•
Tam doldurulmuşmu
Cevaplarda belli bir trend varmı
Sayfalar eksikmi
Son kabul tarihinden sonramı gelmiş
Anket uygun olmayan kişilercemi doldurulmuş
Düzenleme
• Eksik cevaplar olup olmadığına bakılır
• İki seçenek arasına işaret koyma
• Eksik cevaplama
– Eksik cevaplı anketlerde yapılabilecekler
• Anket deneğe tekrar doldurtulur
• Eksik cevapların yerine uygun cevaplar bulunur
– Eksik cevap verenlerin sayısının oransal olarak düşük olduğu,
– Eksik cevaplı anketlerde eksik kısımların az olması
– Eksik olan kısımların araştırma için önem arz eden değişkenlerden olmaması
durumlarında kullanılan yöntemdir
• Eksik cevaplı anketlerin iptal edilmesi
–
–
–
–
Örneklemin büyük olması,
Cevap verenlerle vermeyenler arasında özellikler açısından bir fark olmaması
Cevap vermeyenlerin anketin büyük bir kısmına cevap vermemesi,
Temel değişkenlere cevap verilmemiş olması durumlarında kullanılan
yöntemdir
Kodlama
• Sayısal forma dönüştürmedir. (KODLAMA
ÖRNEKLERİ)
• Her bir cevap seçeneğine karşılık gelen bir kod
(sayı) atanır.
• YENİDEN KODLAMA: kodlanmış olan bir
değişkene ait mevcut kodların yeni kodlarla
değiştirilmesidir.
• Her ankete bir numara verilmelidir (hataların
tespiti).
Verinin bilgisayar ortamına aktarılması
• İnternet anketlerinde ver direk aktarılır
• Veri klavye aracılığı ile giriliyor ise hata yapma
olasılığı yüksektir.
• Hataları görmek için frekans analizi alınır.
Veri temizleme
• Uç değerlerin tespiti (Belli bir markaya ilişkin herşey çok yüksek veya çok
düşük işaretlendi ise ön yargı olma ihtimali düşünülebilir).
• Mantıksal çelişkilerin araştırılması
• Cevap aralığı dışında kalan değerlerin tespiti (ankete giderek kontrol
yapılır).
• Eksik cevaplara çözüm bulma (ilk kontrol elle yapıldı, burada daha detaylı
inceleme yapılır)
– Eksik cevapları yeni değerlerle değiştirirken yapılacaklar
• Mevcut değişkenin ortalamasını almak
• Diğer değişkenlerden yararlanarak mevcut değişken için bir ortalama koymak
• Eksik değerlerin iptal edilmesi
– Tamamen iptal etmek
– Her bir hesaplamada sadece tam olan verilerle analiz yapmak
• Çamaşır makinası olmayan birinin, çamaşır makinası ile ilgili soruları
cevaplaması gibi durumlar
• Kontrol sorusu olarak sorulan soruya çelişkili cevaplar verenlerin tespiti vb.
İstatistiksel Düzenlemeler
• Değişkenlere Ağırlık Atama
• Bazı deneklerin cevaplarına diğerlerine göre daha fazla
ağırlık verme
• Zaman Serisinde son gözlemlere daha fazla ağırlık verme
• Değişkenlerin Yeniden Tanımlanması
• Örneğin aralıklı yaş değişkenini kategorik yapıya
dönüştürmek
• Veri Transformasyonu (Dönüştürme)
• Karekök dönüşümü negatif, logaritma dönüşümü vb
Uygun analiz stratejisinin seçimi
• Araştırmaya ve veriye uygun analiz
belirlenmelidir.
• Cinsiyet verisinde ortalama almak gibi
yanlışlıklar yapılmaktadır…
MERKEZİ EĞİLİM (YIĞILMA) ÖLÇÜLERİ
Puanların bir merkezde toplanma durumunu gösterir
Merkezi Yığılma Ölçüleri
mod
medyan
Aritmetik ortalama
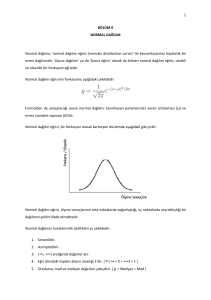
Normal Dağılımda; mod=medyan=aritmetik ortalama bir birine eşittir
ortanca
MEDYAN (ORTANCA)
% 50
% 50
•Dağılımı iki eşit parçaya bölen değerdir (%50 - %50)
• Sıralama türü ölçekler için uygundur
Ham puanların sayısından etkilenir. Uç değerlerden etkilenmez
•Dağılımın tam ortası isteniyorsa, uç değerler ortalamayı etkiliyorsa, ortalamayı
hesaplamak için süre yoksa kullanılır
•Medyan bulunurken puanlar sıraya konulur
•Formülü: Çift sayılarda [(N/2) + (N/2)+(1)]/2
Örnek: Öğrencilerin vizeden aldığı notlar şu şekilde verilmiştir: 68, 71, 74, 80, 82, 88
Ortanca = [(6/2) + (6/2)+1 ] /2 = (3 + 4)/2 = (74+80)/2 = 77 68, 71, 74, (77) 80, 82, 88
Formülü: Tek sayılarda (N+1)/2
Örnek: Öğrencilerin vizeden aldığı notlar şu şekilde verilmiştir: 68, 71, 74, 80, 82
Ortanca = [(5+1)/2] = 3
68, 71, (74) 80, 82
MOD
•Dağılımda en çok tekrar eden değerdir
•Sınıflama türü ölçekler için uygundur
•Ortalama ve ortancanın hesaplanmadığı durumlarda kullanılır
En tipik ölçümler bilinmek isteniyorsa, kabaca hesaplanmak gerekiyorsa moda bakılır
Bir dağılımın birden fazla modu olabilir
•Ardışık eşit sayıda tekrarlanan varsa orta noktasıdır
•Dağılımdaki ölçümlerin hepsi aynı ise mod yoktur
•Uç noktalardan etkilenmez
•En az güvenilen merkezi eğilim ölçüsüdür
•Az sayıdaki ölçümler için uygun değildir
Örnek: Öğrencilerin vizeden aldığı notlar şu şekilde verilmiştir:
68, 71, 71, 74, 80, 80, 80, 80, 82, 88, 88
Cevap: 68, 71, 71, 74, 80, 80, 80, 80, 82, 88, 88
ortanca
MEDYAN (ORTANCA)
% 50
% 50
•Dağılımı iki eşit parçaya bölen değerdir (%50 - %50)
• Sıralama türü ölçekler için uygundur
Ham puanların sayısından etkilenir. Uç değerlerden etkilenmez
•Dağılımın tam ortası isteniyorsa, uç değerler ortalamayı etkiliyorsa, ortalamayı
hesaplamak için süre yoksa kullanılır
•Medyan bulunurken puanlar sıraya konulur
•Formülü: Çift sayılarda [(N/2) + (N/2)+(1)]/2
Örnek: Öğrencilerin vizeden aldığı notlar şu şekilde verilmiştir: 68, 71, 74, 80, 82, 88
Ortanca = [(6/2) + (6/2)+1 ] /2 = (3 + 4)/2 = (74+80)/2 = 77 68, 71, 74, (77) 80, 82, 88
Formülü: Tek sayılarda (N+1)/2
Örnek: Öğrencilerin vizeden aldığı notlar şu şekilde verilmiştir: 68, 71, 74, 80, 82
Ortanca = [(5+1)/2] = 3
68, 71, (74) 80, 82
A. ortalama
ARİTMETİK ORTALAMA
• En çok kullanılan merkezi yığılma ölçüsüdür ( x ) ile gösterilir
•Ölçümlerin toplamının, ölçüm sayısına bölümünü ifade eder
• Dağılımın uç değerlerinden etkilenir
• Bütün ölçümlerin kullanılmasıyla elde edilir
• Dağılım simetrikse, yani çarpık değilse ve üst düzey istatistiksel
işlemler yapılacaksa kullanılır
Öğrenci
1
2
3
4
5
6
Test Puanı
70
70
71
75
75
76
A.O.= (70+70+71+75+75+76) / 6
A.O.= 72.83
Dağılımda Çarpıklık