MATEMAT‹K 6
f, [a, b] de sürekli bir fonksiyon olsun f nin e¤risi x=a, x=b do¤rular›
b
|f(x) | dx dir.
ve x -ekseni ile alan ; S =
a
\
Alan, x- ekseninin üs t ünde ise
b
∀x∈ [a, b] için f(x) ≥ 0 ⇒ S =
f(x) dx dir.
a
Alan, x- ekseninin alt›nda ise
b
∀x∈ [a, b] için f(x) ≤ 0 ⇒ S = -
f(x) dx dir.
a
\
Alan, x ekseninin hem alt›nda hem de üs t ünde ise f, [a,c] de sürekli,
c
b
∀ x ∈[a, c] alan
f(x) dx a
f(x) dx dir.
b
Örnekler :
f(x)= 2x do¤rusu x-ekseni x=1 ve x= 2 do¤rular›yla s›n›rlanan bölgenin alan›n› bulunuz.
2
1.
2
2xdx = x2
= 22- 12 = 4-1 = 3 bulunur.
1
1
2
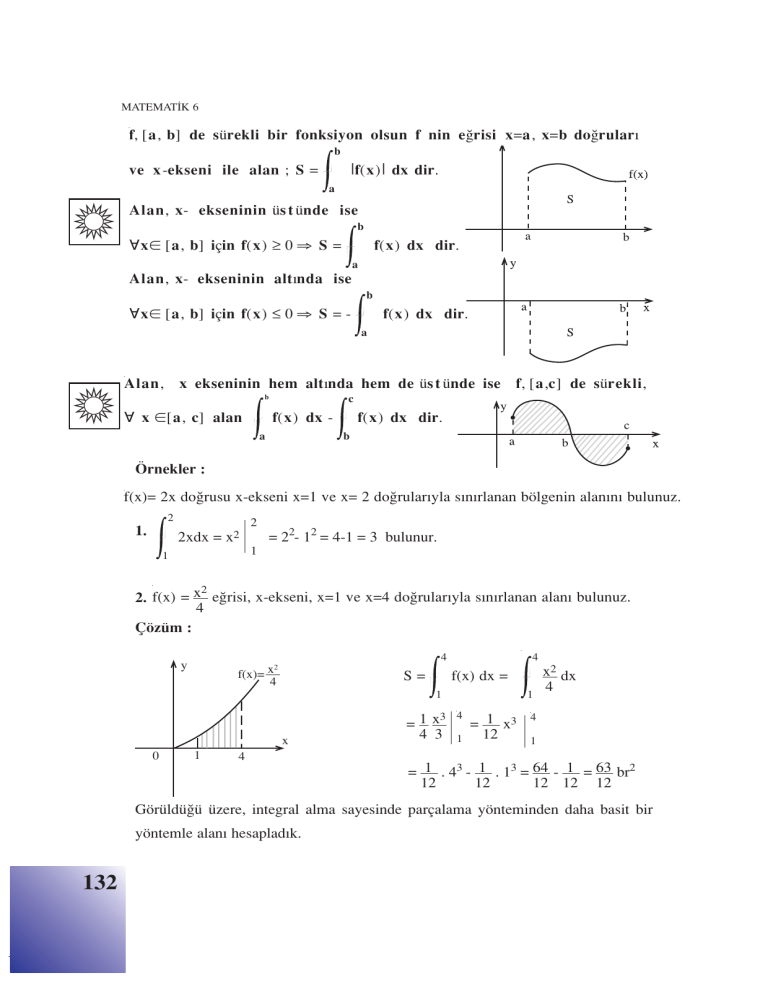
2. f(x) = x e¤risi, x-ekseni, x=1 ve x=4 do¤rular›yla s›n›rlanan alan› bulunuz.
4
Çözüm :
4
y
2
f(x)= x
4
S=
4
f(x) dx =
1
x
0
1
4
3
=1x
4 3
1
4
1
= 1 x3
12
x2 dx
4
4
1
= 1 . 43 - 1 . 13 = 64 - 1 = 63 br2
12
12
12 12 12
Görüldü¤ü üzere, integral alma sayesinde parçalama yönteminden daha basit bir
yöntemle alan› hesaplad›k.
132
MATEMAT‹K 6
f(x) = Sinx e¤risinin [0, π] aral›¤›nda kalan parças› ve x- ekseni ile s›n›rlanan
alan› hesaplay›n›z.
π
π
S=
Sinx dx = - Cosx
0
0
= - (Cosπ - Cos0)
= - (-1) +1 = 1+1
= 2br2
3
|x| dx integralini hesaplay›n›z.
-2
|x| = x, x≥0 ⇒
-x, x<0
b
c
f(x)dxa
b
f(x) dx+
a
f(x) dx
c
C∈[a, b] oldu¤una göre
3
0
|x| dx =
-2
= - 02 -
3
-x dx +
-2
0
3
2 0
2
x
x
+
x dx = 2
2 0
-2
(-2) 2
+ 9 - 0 = 4 + 9 = 13 bulunur.
2
2
2 2 2
133
MATEMAT‹K 6
5. f : R → R ; f(x) = x2+x - 6 e¤risi, x = -2, x = 1 do¤rular› ve x- ekseni ile s›n›rlanan
bölgenin alan›n› bulunuz.
Çözüm :
1
S=-
1
(x2+x-6) dx
f(x) dx =-2
-2
1
3
2
= - x + x - 6x
= -1 - 1 + 6 +
3
2 1 -2
3 2
-8 + 4 + 12 = -2 -3 +36 - 16 + 12 +72 = 99
3 2
6
6
x=-2
= 33 br2
2
x=1
6. f (x) = x3 - 5x2 +6x fonksiyonunun e¤risi ile x- ekseninin s›n›rlad›¤› bölgenin
alan›n› bulunuz.
Çözüm : x(x2-5x+6) = x(x-3) (x-2) = 0 ise
2
3
(x3-5x2+6x) dx -
S=
x =0, x=3, x=2
0
2
4
(x3-5x2+6x) dx = x - 5 x3+3 x2
4 3
2
0
3
4
- x - 5 x3 +3x2
= 4 - 40 +12 - 81 - 45+27-4 + 40 - 12
4
4 3
3
3
2
= 4 - 40 + 12 - 81 + 45 - 27 + 4 - 40 + 12 = 50 - 80 - 81 = 600-563 =37
3
4
3
1
3
4
12
12
(12)
(4)
(3)
134
MATEMAT‹K 6
2
7.
|x–1| dx integralini hesaplay›n›z.
0
Çözüm : x =1 kritik nokta
x-1≥0 ise x–1
x≥1
=
x–1<0 ise -(x-1)
x≤ 1
|x-1| =
1
2
0
0
x-1
-(x-1) oldu¤undan
2
-(x-1) dx+
|x-1| dx =
;
;
1
1
2
2
2
+ x -x
(x-1) dx = -x + x
2
2
0
1
= -1 + 1 + 2 - 2 - 1 + 1 = - 2 + 2 = -1 + 2 = 1 bulunur.
2
2
2
3
[|x|] x dx integralini hesaplay›n›z.
8.
0
Çözüm :
x ∈[0, 1) ⇒ f(x) = [|x|] = 0
x ∈[1, 2) ⇒ f(x) = [|x|] = 1
x ∈[2, 3) ⇒ f(x) = [|x|] = 2
3
1
[|x|]x dx =
0
2
0 dx +
0
3
xdx+
1
2
2
3
2
2x dx = 0+ x + x2
2 1
2
2 - 1 + 9 - 4 = 3 + 5 = 13 bulunur.
2
2
2
4
sgn (x2 - 3x+2)dx integralini hesaplay›n›z.
9.
-1
Çözüm :
1 ; f(x) > 0 ise
0 ; f(x) = 0 ise
-1 ; f(x) < 0 ise
f(x) in iflaretini inceleyelim.
Sgn f(x) =
135
MATEMAT‹K 6
x
-∞
1
x2 - 3x+2
+
O
4
1
Sgn
(x2-3x+2)dx
=
-1
2
dx+
-1
2
1
x
+ (-x)
+∞
O
+
4
-1dx+
1
1dx=
2
4
+x
1
-1
_
2
= (1+1) - (2-1) + (4-2) = 2 - 1+2 = 3 bulunur.
2
2
[|x|] Sgnx dx integralini hesaplay›n›z.
10. x≠0 için
-1
Çözüm :
x ∈[-1, 0) ⇒ [|x|] = -1
1 ; x>0 ise
Sgnx = -1 ; x<0 ise
0 ; x=0 ise
x ∈[0, 1) ⇒ [|x|] = 0
x ∈[1, 2] ⇒ [|x|] = 1
2
0
[|x|]
Sgnx
1
-1
dx =
(-1) dx +
-1
-1
0
=
2
-dx +
-1
11.
0
1
π
2
0 dx +
0
dx = - x
1 dx
1
2
+x
-1
2
= -1 + 2 -1 = 0
1
|Cosx-Sinx| dx integralini hesaplay›n›z.
0
Çözüm :
0, π aral›¤›nda Cosx -Sinx = 0 denkleminin kökü x = π tür.
2
4
x≤ π için Cosx≥ Sinx ve |Cosx-Sinx| = Cosx - Sinx
4
x> π için Cosx< Sinx ve |Cosx -Sinx| =-(Cosx - Sinx)
4
= Sinx - Cosx dir.
136
MATEMAT‹K 6
π
4
π
2
|Cosx - Sinx| dx =
π
2
(Cosx - Sinx) dx +
0
π
4
Cosx dx +
π
2
Sinx dx -
π
4
0
π
4
0
= Sinx
- Cosx
π
4
Sinx dx -
+ Cosx
Cosx dx
π
4
0
π
2
π
4
π
2
(Sinx - Cosx) dx
π
4
0
π
4
0
- Sinx
π
2
π
4
= (Sin π - Sin0) - Cos π - Cosπ + Cos π - Cos0 - Sinπ - Sin π
4
2
4
4
2
4
2 - 0 - 0 - 2 + 2 -1 - 1 - 2
2
2
2
2
=
= 2 + 2 + 2 -1-1+ 2 = 4 2 = 2 2 -1 bulunur.
2
2
2
2 2
12. Afla¤›daki integralleri hesaplayal›m.
3
3
3
(x2-4x+2) dx = x - 4 x2+2x
= 27 - 18+6 - 1 +2-2 =
3 2
3
3
1
a)
1
-3 - 1 = - 10 bulunur.
3
3
Cos(-θ) = Cosθ ; Sin(-θ) = -Sinθ
3
b)
1
= -2 (Cos1 - Cos(-1))
(2Sinx+2Cosx) dx = (-2 Cosx + 2 Sinx)
-1
-1
+2 (Sin(1) - Sin (-1)) = -2 (Cos(1) - Cos(1)) + 2 (Sin (1) + Sin(1)) = 4 Sin1
π/4
π
1 dx = tgx 4
Cos 2x
0
c) S =
0
π/2
d) S =
0
= tan π - tg0 = 1-0 = 1
4
-1 dx = Arc cosx π2 = Arc cos π - Arc cos0
2
1-x2
0
137
MATEMAT‹K 6
1
1
1 dx = Arctgx
= Arctg 1- Arctg0 = π - 0 = π
0
1+x2
4
4
e) S =
0
1
1
e 5x dx = 1 e 5x
= 1 (e 5.1-e 5.0) = 1 (e 5-1)
5
5
5
0
f) S =
0
5
= e -1
2 5
bulunur.
π
g) S =
Sin |x| dx =
Sin(-x) dx+
0
-π
π
0
Sinx dx =
-π
-π
Cosx
π
0
0
-Sinx dx+
-π
Sinx dx =
0
π
- Cosx
0
= Cos0 - Cos(-π) - Cosπ + Cos0 = 1 - (-1) - (-1) +1 =
1+1+1+1 = 4 bulunur.
2
0
h)
Sgn[|x|] dx =
-1
0
=
-1
2
0dx +
0
2
[|x|]
[|x|]
dx =
1
3
2
1
3
+
4x
2
3
= 2-1+12-8+108-81 = 86
3
2π
[|Sinx|] Sinx dx =
π
33dx =
4
+ 27x
2π
j)
4
2 dx+
2
= (-1) +2 -1 = 0 d›r.
1
2
1 dx+
1
2
+x
-1
1
Sgn(1) dx
1
0
dx = -x
1
4
›)
Sgn (0) dx +
0
1
-dx+
2
Sgn (-1) dx+
-1
x
1
-Sinx dx = Cosx
π
2π
= Cos2π - Cosπ
π
= 1-(-1) = 1+1 = 2 dir.
x, π den 2π ye kadar de¤iflti¤inde Sinx, -1 ile 0 aras›nda de¤iflir. [|Sinx|] =-1 dir.
138
MATEMAT‹K 6
3
k)
2
1
|x2-3x+2|
( x2-3x+2)dx+
dx=
0
-
1
x3 - 3 x2 +2x
3 2
-
0
(x 2-3x+2) dx
dx +
1
0
3
= x -3 x2+2x)
3 2
3
(x2-3x+2)
2
2
3
3
+ x - 3 x2+2x
1 3 2
2
= 1 - 3 +1 - 8 +12 +4- 1 +3 -2 + 27 - 27 +6- 8 + 12 -4
3 2
3 2
3 2
3 2
3 2
= 2-9+6 - 16+36+24-2+9-12 + 54-81+36-16+36-24 - 1+71+5 = 75 = 25
6
6
6
6
6
2
4
2
Sgn(x2-5x+6)
l)
dx =
1
1dx1
x
x2-5x+6
3
2
+
O
4
1dx = x
1dx+
2
2
+x
=
3
2
2-1-(3-2) + 4-3 = 1-1+1 = 1 bulunur.
3
-
x
1
3
4
3
-
O +
13. f: (x) = -x2+7x-6 fonksiyonunun e¤risi x = 2, x=5 do¤rular› ve x-ekseni ile
s›n›rlanan bölgenin alan›n› bulunuz.
Çözüm :
5
S=
5
(-x2+7x-6) dx
f(x) dx =
2
3
2
= - x + 7x - 6x
3
2
2
5
2
= - 125 + 175 - 30 - -8 + 14-12
3
2
3
= 189
2
139
MATEMAT‹K 6
14. f(x) = |x2-3x-4| fonksiyonunun e¤risi ile x-ekseninin s›n›rland›¤› bölgenin
alan›n› bulunuz.
Çözüm :
f(x) = (x-3 )2 - 25
4
2
4
S=-1
4
3
(x2-3x-4) dx = (- x + 3 x2 +4x)
3 2
-1
= - 64 +24+16 - 1 +3 -4
3 2
3
= 141
6
15. f(x) = x2 -8x fonksiyonunun e¤risine x -ekseni ile s›n›rlanan bölgenin alan›n›
bulunuz.
f(x) =x2 -8x =(x-4) 2 -16
8
S =-
8
(x 2-8x) dx
f(x) dx =
0
0
8
3
= x - 4x2
=
3
0
3
8
- 4.64 = 512 - 256
3
3
256
=
br2 bulunur.
3
140
MATEMAT‹K 6
16. f(x) =Sinx fonksiyonunun e¤risi ile x = π , x = 7π do¤rular› ve x- ekseni ile
2
4
s›n›rlanan bölgenin alan›n› bulunuz.
Çözüm :
π
S=
Sinx dxπ
2
7π
4
π
Sinx dx = - Cosx
π
π
2
+ Cosx
7π
4
π
= - Cosπ + Cos π + Cos 7π - Cosπ = 1+ 2 + 2 +1 = 2+ 2 br2
2
2
4
4
17. Afla¤›daki integralleri hesaplay›n›z.
5
a)
Sin
[|x|] π
2
0
1
dx =
1
=
2
Sin 2π dx =
4
2
0 dx +
0
2
3
1 dx +
1
4
dx 1
1
Sinπ dx
5
Sin 3π dx +
2
3
3
Sin π dx +
2
Sin0 dx +
0
4
+
2
3
4
0 dx +
2
2
4
dx = x
- x
1
3
5
-dx +
3
0 dx =
4
= (2-1) - (4-3) = 1-1 = 0
141
MATEMAT‹K 6
π
2
b)
π
4
-1 dx = Cotgx
Sin2x
e
1 dx = lnx
x
c)
1
e
π
2
π
4
= Cotg π - Cotg π = 0-1= -1
2
4
= lne-ln1 = 1-0 = 1 dir.
1
‹K‹ E⁄R‹ ‹LE SINIRLANAN BÖLGEN‹N ALANI
Örnekler :
2
1. y = x do¤rusu ve y = x parabolünün s›n›rlad›¤› bölgenin alan›n› bulunuz.
2
Çözüm :
E¤riyle do¤ruyu birlikte çözelim ve s›n›rlar›n› bulal›m. Sonra grafi¤ini çizip,
arada kalan bölgeyi tan›mlayal›m.
2
x = x ⇒ x2-2x = 0 ⇒ x(x-2) = 0 ⇒
2
x1 = 0 veya x-2 = 0 ⇒ x2 = 2 dir.
2
S=
0
2
=x
2
142
2
2
(x- x ) dx =
2
2
0
3 2
-x
6
0
2
x dx 0
0
= 2- 4 = 2 br2
3 3
x2 dx
2
MATEMAT‹K 6
2. y = x2, y = - x2+2x fonksiyonlar›n›n e¤rileri ile s›n›rl› bölgenin alan›n› bulunuz.
Çözüm :
y = - x2+2x = -(x-1) 2+1
1
(-x2+2x-x2) dx = - 2
S=
1
1
1 3
x2 dx +2
0
0
0
x dx = -2 x
3
1
+
0
2
2 x
0 2
= - 2 (1-0) + (1-0) = - 2 +1 = 1 br2
3
3
3
3. y = 2x2 e¤risi ve y = 4x do¤rusu ile s›n›rlanan bölgenin alan›n› bulunuz.
Çözüm :
E¤ri ile do¤ruyu ortak çözelim.
4x = 2x2 ⇒ 2x = x2
x1 = 0 veya x2 = 2
2
2
(4x-2x2) dx= 4
S=
0
2
x dx -2
0
0
2 2
3 2
x2 dx = 4 x
-2 x
2 0
3 0
= 2.4 - 16 = 8 - 16 = 8 br2
3
3 3
143
MATEMAT‹K 6
4. 0, π aral›¤›nda, y = Sinx , y = Cosx e¤rileri ve x- ekseni ile s›n›rlanan bölgenin
2
alan›n› bulunuz.
Çözüm :
π/4
S=
π/2
Sinx dx +
Cosx dx = -Cosx
π/4
0
π
4
0
+ Sinx
π
2
π
4
= - Cos π + Cos0 + Sin π - Sin π = - 2 +1 +1 - 2 = 2- 2
2
2
4
2
4
5. y2 = 3x ve x2 = 3y e¤rileri ile s›n›rlanan bölgenin alan›n› bulunuz.
2
y=x
3
2
(x )2 = 3x
3
x4 = 3x
9
Çözüm :
x4 -27x = 0
x(x3 - 27) = 0
x1 = 0 veya x2 = 3
x=
3
S=
3
3x -
x2
0
=2 3
3
144
x3
3
3
dx =
0
3 3
-x
9 0
0
y2
⇒ y = 3x
3
3
3 x dx - 1
3
x2 dx =
0
= 2 3 2 3 27 - 3 = 12 3 -3 br2
3
MATEMAT‹K 6
6. y = x2 -1 e¤risi ve y = x-1 do¤rusunun s›n›rland›¤› bölgenin alan›n› bulunuz.
Çözüm :
1
S=
1
(x-1) -
(x2-1)
dx =
0
0
1
2
3
(x-x2) dx= x - x
=
2 3 0
( 1 - 1 ) = 3 - 2 = 1 br2
2
3
(3) (2)
6
6
6
7. y = x2 -8 ve y = -x2 e¤rileri ile s›n›rlanan bölgenin alan›n› bulunuz.
Çözüm :
x2 - 8 = -x2
2x2 = 8
x2 = 4
x1 = 2 , x2 = -2
2
2
(-x2 -x2
S=
-2
+8) dx =
-2
2
(-2x2 +8) dx = ( -2 x3 +8x)
3
-2
= - 2 8+8.2 - -2 (-8) -16 = - 16 + 16 - 16 + 16
3
3
3
3
= - 32 + 32 = 96-32 = 64 br2
3
1
3
3
(1) (3)
145
