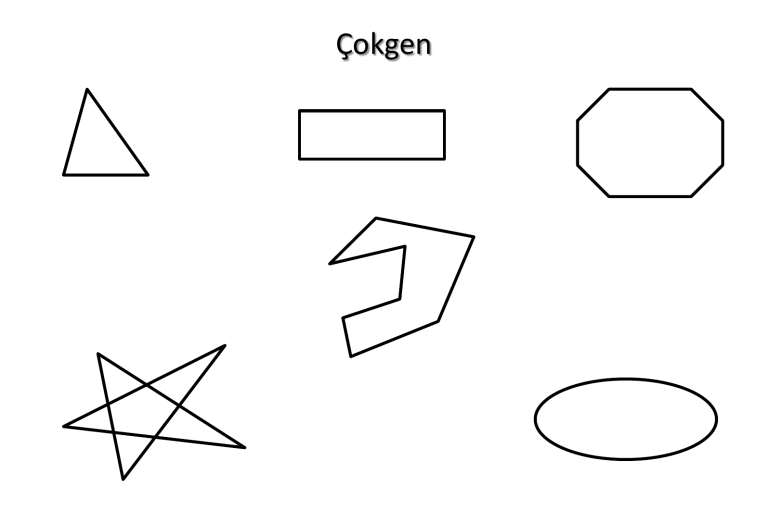
Çokgen
Çokgensel bölge
İç bükey – Dış bükey çokgen
Çokgenin temel elemanları
Köşeleri:
Kenarları:
İç açıları:
Dış açıları:
Köşegenleri:
Kenar – Köşegen ilişkisi
Bir köşe belirleyiniz ve belirlediğiniz köşeden geçen kaç tane köşegen olduğunu bulunuz.
Genelleyiniz.
Kenar – Açı ilişkisi
Kenar sayısına göre iç açılarının toplamını ve dış açılarının toplamını bulunuz. Genelleyiniz.
Bir çokgenin temel elemanlarıyla belirlenmesi
n kenarlı bir çokgenin, en az n – 2 tane uzunluk olmak üzere, 2n – 3 tane temel elemanının
verilmesiyle belirlenir.
Üçgen ve temel elemanları
Köşeleri:
Kenarları:
Açıları (iç açıları):
Dış açıları:
İç açılar toplamı:
Dış açılar toplamı:
Açılarına göre üçgen çeşitleri
Kenarlarına göre üçgen çeşitleri
Üçgenin kenarortayları – Ağırlık merkezi
Üçgenin yükseklikleri – Diklik merkezi
Bir köşeye ait yardımcı elemanlar
ha nA va
Üçgenin açıortayları – İç merkez
Üçgenin dış açıortayları – Dış merkez
Ödev 1
Ödev 2
Ödev 3
Ödev 4
Ödev 5
Ödev 6
Ödev 7
Ödev 8
Ödev 9
Ödev 10
Ödev 11
Ödev 12
Ödev 13
Adı Soyadı:
Sınıf:
No:
Ödev kontrol tarihi:
Açı – Kenar ilişkileri 1
Üçgenin açısı büyürse karşısındaki kenar da büyür, açı
küçülürse karşısındaki kenar da küçülür.
Örnek
m(B) m(C) b c
olduğunu ispatlayınız.
Genelleme
m(A) m(B) m(C)
Açı – Kenar ilişkileri 2
Üçgen eşitsizliği: Bir üçgende herhangi bir kenarın uzunluğu, diğer iki kenarın uzunluklarının
toplamı ile farkı arasındadır.
bc abc
b
c
İspat
Alıştırma 1
İki kenarı 3 ve 4 cm olan üçgenin diğer kenar uzunluğunun alacağı tam sayı değerleri bulunuz ve
bu değerlere göre değişen uzunluğun karşısındaki açı çeşidini yazınız.
Alıştırma 2
B geniş açı olduğuna göre
x in alabileceği değer
aralığını bulunuz.
Alıştırma 3
B geniş açı olduğuna göre
x in alabileceği değer
aralığını bulunuz.
Ödev 1
x in değer aralığını bulunuz.
6
x
3
10
6
12
5
x
x
Ödev 2
Ödev 3
Ödev 4
Ödev 5
Ödev 6
Ödev 7
Ödev 8
Ödev 9
Ödev 10
Ödev 11
Adı Soyadı:
Sınıf:
No:
Kontrol tarihi:
Sinüs teoremi
İspat 1:
1
1
1
S bcsinA acsinB absinC
2
2
2
a
b
c
2R
sinA sinB sinC
R : çevrel çemberin yarı çapı
İspat 2:
sin A =
Sinüs oranı ile ilgili ansiklopedik bilgiler
a
b
c
a
b
c
2R
sinA sinB sinC sin(B C) sin(A C) sin(A B)
A + B + C = 180o
sin A = sin (180o – A) = sin (B+C)
sin(B C) sinBcosC sinBcosC
1
1
1
A(ABC) ab sin(A B) ac sin(A C) bc sin(B C)
2
2
2
sin(B C) sinBcosC sinBcosC
1
1
1
A(ABC) ab sinC ac sinB bc sinA
2
2
2
BC
BC
cos
2
2
A(ABC) 2R2 sinA sinB sinC
sinB sinC 2sin
sinB sinC
1
cos(B C) cos(B C)
2
sinA cos(90o A)
A
A
sinA 2sin cos
2
2
sinA 1 cos2 A
sin30o sin150o
1
2
sin45o sin135o
2
2
3
2
sin0o sin180o 0
sin60o sin120o
sin90o 1
Alıştırma 1
2k
....
....
2k
....
....
....
....
....
3k
....
....
k
3k
....
2k
2k
Sinüs teoremi sonucu
3k
2k
2k
2k
2k
k
6 2
k
2
3k
6 2
2
k
k
6 2
k
2
2
6 2
2k
k
6 2
k
2
3k
2k
2k
6 2
k
2
150°
75°
6 2
k
2
165°
15°
6 2
k
2
Alıştırma 2
12
x
2. yol: ek çizim
12
x
Alıştırma 3
6 3
x
2. yol: ek çizim
6 3
x
Alıştırma 4
xy ?
2
2. yol: ek çizim
Ödev 1
Çevre(ABC)=?
Ödev 2
xy ?
2 3
xy ?
2
Ödev 3
Ödev 4
Kosinüs teoremi (hatırlatma)
AC AB BC
A
AC AB BC
2
c
AC AB BC
b
2
2
AC AB BC AB BC
B
a
C
2
AC AB AB 2AB BC BC BC
a2
BA
b a c 2ac cosB
2
c2
2
2
2
2
2
AC AB BC 2 BA BC cosB
b2 a2 c2 2ac cosB
cos90o 0 b2 a2 c2
Kosinüs oranı ile ilgili ansiklopedik bilgiler
A + B + C = 180o
a2 b2 c2 2bc cos A
cos A = – cos (180o – A) = – cos (B+C)
b2 a2 c2 2ac cosB
cos(B C) cosBcosC sinBsinC
cos(B C) cosBcosC sinBsinC
cosB cosC 2cos
cosB cosC
BC
BC
cos
2
2
1
cos(B C) cos(B C)
2
cos A sin(90o A)
cos A cos2
A
A
sin2
2
2
cosA 1 sin2 A
c2 a2 b2 2ab cosC
b2 c2 a2
cos A
2bc
a2 c2 b2
cosB
2ac
a2 b2 c2
cosC
2ab
cos30o sin60o
3
2
cos45o sin45o
2
2
cos60o sin30o
1
2
cos90o sin0o 0
cos180o cos0o 1
cos150o cos30o
3
2
cos135o cos45o
2
2
cos120o cos60o
1
2
Alıştırma 1
Alıştırma 2
2. yol
Alıştırma 3
Ödev 1
Ödev 2
Ödev 3
Üçgenin kenarını bölen nokta
n'
D noktası, ABC üçgeninin [BC] kenarını
D’ noktası; ABC üçgeninin [BC] kenarını
DB m
DC
n oranında içten bölen noktadır.
D'B m'
oranında dıştan bölen noktadır.
D'C
n'
Özel olarak;
AB
BD
BD'
[AD] iç açıortay, [AD']dış açıortay olur.
AC
CD
CD'
BD
[AD] kenarorta olur.
CD
Açıortay
[AD]: iç açıortay
[AD’]: dış açıortay
n'
AB
BD
BD'
AC
CD
CD'
oranlarıyla elde edilen D ve D’ noktalarına sırasıyla iç açıortay ayağı ve
dış açıortay ayağı denir.
Açıortay uzunlukları x ve x’ ile gösterilirse;
x 2 bc mn
x'2 m'n' bc
Alıştırma 1
Alıştırma 2
Alıştırma 3
Üçgenin iç merkezi
Herhangi bir üçgenin iç açıortayları tek noktada kesişir. Bu noktaya (K) üçgenin iç merkezi denir.
Üçgenin iç merkezi, iç teğet çemberinin de merkezidir.
Açıortay üzerindeki bir noktadan
kenarlara inilen dikmeler eşittir.
K
Üçgenin dış merkezi
Herhangi bir üçgenin iki dış açıortayı ile diğer iç açıortayı tek noktada kesişir. Bu noktaya üçgenin
dış merkezi denir. Üçgenin üç tane dış merkezi vardır.
AK
KD
BK
KE
F
E
D
CK
KF
Dış teğet çemberler
Üçgenin dış merkezleri, dış teğet çemberlerin merkezidir.
Alıştırma 1
Alıştırma 2
AE
?
ED
20
Ödev 1
Ödev 2
Ödev 3
Ödev 4
Ödev 5
Ödev 6
Ödev 7
Ödev 8
Ödev 9
Ödev 10
x
Ödev 11
Ödev 12
Kenarortay 1
2ax .........
Va
a2
2 v a b2 c 2
2
2
2 vb2
2 v c2
2
2
a
2
Alıştırma
Kenarortay 2
a2
2 va
b2 c 2
2
b2
2
2 vb
a2 c2
2
c2
2
2 v c a2 b2
2
_________________
2
v a2 v b 2 v c 2 3
a2 b2 c2
4
Alıştırma
a) Va2 Vb2 Vc2 ?
b) Kenarortayları küçükten büyüğe sıralayınız.
Kenarortay 3
AG
BD DC
BC
k
Muhteşem üçlü : BD = DC = AD, m(A)= 90o
mA 90o v a
v a2 v b 2 v c 2
a
2Va2
2
b2 c 2
3
4
a
2
AG
BD DC
5v a2 vb2 v c2
BC
k
2
a
2Va2
b c a2 b2 c2 , 5va2 vb2 vc2
vb vc va2 vb2 vc2 , 5a2 b2 c2
Alıştırma 1
17
Alıştırma 2
a) A ile K noktaları arasındaki uzaklık ?
b) x2 + y2 = ?
Kenarortay 4
A
Köşeleri A(x1, y1), B(x2, y2), C(x3, y3)
olan ABC üçgensel bölgenin ağırlık
merkezi G(x0, y0) ise;
E
G
D noktasının koordinatları:
B
G noktasının koordinatları:
x0
y0
x1 x 2 x 3
y1 y 2 y 3
D
C
Alıştırma
y
A
AOB üçgensel bölgenin ağırlık merkezi G(6,8)
olduğuna göre,
2
G
2
a) AG GB ?
b) A noktası ile B noktasının koordinatları toplamı kaçtır?
x
O
B
Ödev 1
Ödev 2
Ödev 3
Ödev 4
Ödev 5
Ödev 6
Ödev 7
Ödev 9
Ödev 10
Ödev 11
Ödev 12
Ödev 13
Yükseklik
Herhangi bir üçgenin yükseklikleri tek
noktada kesişir , bu noktaya üçgenin diklik
merkezi denir.
Verilen üçgenlerde ha, hb ve hc yükseklik
uzunluklarını ve diklik merkezlerini
gösteriniz.
Köşelerinin koordinatları verilen üçgenin
yüksekliklerinden birini hangi yöntemleri
kullanarak bulabilirsiniz. Tartışınız.
Araştırma – İnceleme
b vektörünün a vektörü üzerindeki
dik izdüşüm vektörü b’ vektörü ise
b
b'
b'
a
ba
a
aa
Köşelerinin koordinatları verilen bir
üçgenin, dikme ayaklarının
koordinatlarının bulunması için
kullanılabilir. İki nokta arasındaki
uzaklık ile yükseklikler de
bulunabilir.
Alıştırma
Köşeleri A(1, 2), B(3, 4), C(4, 1) olan ABC üçgeninin C noktasından çizilen yüksekliğin dikme ayağı
D ve diklik merkezi H noktasıdır.
a) D dikme ayağının koordinatlarını bulunuz.
b) [CD] yüksekliğinin uzunluğunu bulunuz.
c) Bu üçgenin yüksekliklerinin tek noktada kesiştiğini göstermek için hangi adımların yapılması
gerektiğini söyleyiniz.
Üçgensel bölgenin alanı
Üçgenin alanı denildiğinde, üçgensel bölgenin alanı
düşünülür.
Üçgen alanı = (taban x yükseklik) / 2
Üçgen alanı = dikdörtgen alanı / 2
Üçgen alanı = paralelkenar alanı / 2
Temel alan formülü ve yorumları 1
A
A(ABC) s a
2s
2s
2s
, b , c
ha
hb
hc
bc abc
ha
2s 2s 2s 2s 2s
hb hc
ha hb hc
C
B
a
A(ABC)
aha bhb chc
2
2
2
1 1
1
1
1
hb hc ha hb hc
Alıştırma
Bir ABC üçgeninde,
ha = 3 cm, hb = 4 cm olduğuna göre
hc nin değer aralığı nedir?
Temel alan formülü ve yorumları 2
1) Yükseklik ve tabanları aynı olan üçgenlerin alanları da eşittir.
2) Yükseklikleri aynı olan üçgenlerin alanları oranı tabanları oranına eşittir.
D
C
A
E
A
B
A(DAB) A(CAB)
A(ADC) A(BDC)
A(EAD) A(EBC)
B
m
D
A(ABD) m
A(ADC) n
A(ABD)
m
A(ABC) m n
n
C
Alıştırma 1
Taralı alanı =?
10
5
Alıştırma 2
Alıştırma 3
Sinüs alan ve yorumları
A
A
A
n
m
n
m
E
E
c
D
B
a
1
A(ABC) acsinB
2
C
t
D
p
B
C
TA m n
A b c
B
r
s
TA m r t p s n
A
a b c
C
Alıştırma 1
Alıştırma 2
Alıştırma 3
3a
paralelkenar
s1
?
s2
a
s1
4b
7b
3b
s2
Heron alan formülü
A
Örnek
Kenar uzunlukları 5, 6 ve 7 cm olan üçgenin alanını bulunuz.
b
c
B
a
C
A(ABC) u(u a)(u b)(u c)
u
ab c
2
Alan formülü ile R nin bulunuşu
Örnek
Kenar uzunlukları 5, 6 ve 7 cm olan üçgenin çevrel çember
yarı çapını bulunuz.
A(ABC) s
S
abc
4R
Alan formülü ile r nin bulunuşu
A(ABC) s
S u r
u
ab c
2
Örnek
Kenar uzunlukları 5, 6 ve 7 cm olan üçgenin iç teğet
çemberinin yarı çapını bulunuz.
Ödev 1
Ödev 2
Ödev 3
Ödev 4
Ödev 5
ABC üçgeninde ha = 6 cm, Va = 8 cm olduğuna
göre, nA hangi aralıkta değer alır?
Ödev 6
Ödev 7
Ödev 8
Köşeleri A(-4, 3), B(0, -2), C(-3, 0) olan üçgenin [BC]
kenarına ait yükseklik ayağının koordinatları toplamı
kaçtır?
ABC üçgeninin [BC] kenarına ait yükseklik
ayağı H noktasıdır.
BA=(2,6) ve BC=(8,0) olduğuna göre,
H noktasının koordinatları toplamı kaçtır?
Ödev 9
Ödev 10
Ödev 11
Ödev 12
Ödev 13
Ödev 14
A
1
3
E
5
D
1
B
2
2
C
Ödev 15
dikdörtgen
paralelkenar
Karnot teoremi
C' AB,B' AC,A' BC
A
B
C'
C
A'
A
B'
Bir üçgende kenar doğrularından çıkılan dikmelerin tek
noktada kesişmesi için gerek ve yeter şart:
2
2
2
2
2
2
AC' C'B BA' A'C CB' B'A 0
Alıştırma 1
c/2
Üçgenlerin kenar orta dikmeleri tek
noktada kesişir, bu nokta çevrel çember
merkezidir.
b/2
2
2
2
2
2
2
2
2
?
AC' C'B BA' A'C CB' B'A 0
c/2
b/2
a/2
a/2
2
2
2
2
c c a a b b
0
2 2 2 2 2 2
Alıştırma 2
Üçgenlerin açıortayları tek noktada
kesişir, bu nokta iç teğet çember
merkezidir.
2
2
2
2
2
2
?
AC' C'B BA' A'C CB' B'A 0
n2 n2 m2 m2 p2 p2 0
Alıştırma 3
Üçgenlerin yükseklikleri tek noktada
kesişir. Bu nokta diklik merkezidir.
2
AK x 2 n2 y 2 t2
2
BK z2 p2 x 2 m2
2
CK y 2 s2 z2 r2
____________
n2 p2 s2 t2 m2 r2
n2 m2 p2 r2 s2 t2 0
2
2
2
2
2
2
AC' C'B BA' A'C CB' B'A 0
Alıştırma 4
Bir üçgenin iki dış açıortayı ile diğer iç
açıortayı tek noktada kesişir. Bu nokta
dış teğet çember merkezidir.
AC' B'A
C'B BA'
A'C CB'
2
2
2
2
2
2
AC' C'B BA' A'C CB' B'A 0
Alıştırma 5
Genel karnot teoremi
A1A2A3A4A5 …An herhangi bir çokgen olmak üzere, çokgen düzleminde alınan
bir noktadan sırasıyla ardışık A1A2, A2A3, A3A4, …AnA1 kenar doğrularına inilen
dikme ayakları A’1, A’2, A’3, …, An ise
2
2
2
2
2
2
A1A'1 A'1 A2 A2A'2 A'2 A 3 ... AnA'n A'n A1 0
Bu bağıntı sağlanıyorsa A’1, A’2, A’3, …, An noktalarından çıkılan dikmeler tek noktada kesişir.