matemat˙ık ı ders˙ı c¸alısma soruları (esk˙ı sınav

x2 − 2x − 3
x→−1 x sin(x + 1)
√
2 − 5 − x2
b) lim
x→1
1−x
MATEMATİK BÖLÜMÜ
MAT 101 - MATEMATİK I DERSİ
ÇALIŞMA SORULARI
(ESKİ SINAV SORULARI)
1) 2x + sin2 x −
gösteriniz.
1
2
a) lim
c) lim
denkleminin tek çözümü olduğunu
x→−2
|2x + 4|
x2 − 4
Not: İki farklı yol ile çözmeye çalışınız. Biri ara
değer teoremi (özel olarak Bolzano teoremi) ile diğer
Rolle teoremi yardımı ile.
8) f (x)
2) Aşağıdaki limitleri (eğer
(L’Hospital kullanmayınız)
varsa)

x+1

x < 0 ise;
 x ,
=
2,
x = 0 ise; fonksiyonunun


|x − 2|, x > 0 ise.
grafiğini bilinen fonksiyon grafikleri yardımı ile
çiziniz (varsa kesenlerini, asimptotlarını gösteriniz).
Ayrıca sürekli ve/veya türevli olmadığı noktaları
belirtiniz.
hesaplayınız.
1
x + x2 + 4x
1 − cos2 x
b) lim
x→−π 1 + cos3 x
sin(2|x|)
c) lim
x→0
x
(1 − 2x)(1 + x2 ) − 1
d) lim
x→0
x
a)
lim
x→−∞
√
3) −1 ≤ x ≤ 1 olmak üzere, f (x) =
tanımlanıyor.
√
x+5
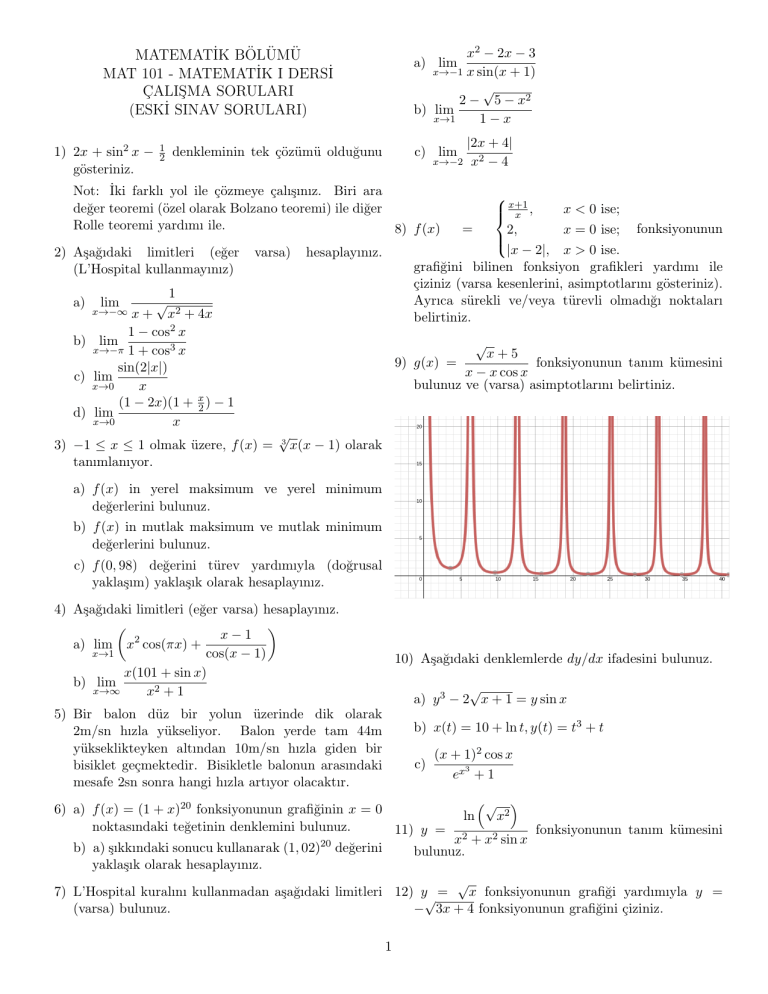
9) g(x) =
fonksiyonunun tanım kümesini
x − x cos x
bulunuz ve (varsa) asimptotlarını belirtiniz.
√
3
x(x − 1) olarak
a) f (x) in yerel maksimum ve yerel minimum
değerlerini bulunuz.
b) f (x) in mutlak maksimum ve mutlak minimum
değerlerini bulunuz.
c) f (0, 98) değerini türev yardımıyla (doğrusal
yaklaşım) yaklaşık olarak hesaplayınız.
4) Aşağıdaki limitleri (eğer varsa) hesaplayınız.
x−1
2
a) lim x cos(πx) +
x→1
cos(x − 1)
x(101 + sin x)
b) lim
x→∞
x2 + 1
10) Aşağıdaki denklemlerde dy/dx ifadesini bulunuz.
√
a) y 3 − 2 x + 1 = y sin x
5) Bir balon düz bir yolun üzerinde dik olarak
2m/sn hızla yükseliyor. Balon yerde tam 44m
yükseklikteyken altından 10m/sn hızla giden bir
bisiklet geçmektedir. Bisikletle balonun arasındaki
mesafe 2sn sonra hangi hızla artıyor olacaktır.
b) x(t) = 10 + ln t, y(t) = t3 + t
c)
(x + 1)2 cos x
ex3 + 1
√ 6) a) f (x) = (1 + x)20 fonksiyonunun grafiğinin x = 0
ln
x2
noktasındaki teğetinin denklemini bulunuz.
11) y = 2
fonksiyonunun tanım kümesini
x + x2 sin x
b) a) şıkkındaki sonucu kullanarak (1, 02)20 değerini
bulunuz.
yaklaşık olarak hesaplayınız.
√
7) L’Hospital kuralını kullanmadan aşağıdaki limitleri 12) y√ =
x fonksiyonunun grafiği yardımıyla y =
(varsa) bulunuz.
− 3x + 4 fonksiyonunun grafiğini çiziniz.
1
sin2 x
x→π 1 + cos3 x
1 − cos x
k) lim
x→0
x
ex − e−100x
l) lim x
x→∞ e + e−100x
sin 2|x|
m) lim
x
x→0−
1
n) lim sin x cos 2
x→0
x
x2 tan x
o) lim
x→0 3 sin(x3 )
1
13) Aşağıda verilen fonksiyonların türevlerini bulunuz.
p) lim √
x→−∞
x2 + 4x + x
1
2

+ e3x tan(2x + 1) + ln(sin x)
a) y = √
2

x − 1, x < 1 ise;
x+1
√
2
18) f (x)
=
olarak
−x + 1, x > 1 ise;
b) y = x x+1 + 2(x −1)


1,
x = 1 ise.
3
5
14) y = 1 + 40x − 3x eğrisi üzerindeki noktalardan
tanımlanıyor.
hangisinden çizilen teğetin eğimi en fazladır.
a) f fonksiyonu x0 = 1 noktasında sürekli midir?
y
x
Neden?
15) x + y = 3 olmak üzere
j) lim
dy
=?
dx dy b)
dx b) f nin grafiğini bilinen fonksiyon grafikleri
yardımıyla çiziniz.
a)
19) Aşağıdaki sorularda dy/dx ifadesini bulunuz.
q
2)
a) y = sin(x
tan x
=?
(x,y)=(1,2)
√
16) 119 ≈?
b) y = xsin x
17) L’Hospital kuralını kullanmadan aşağıdaki limitleri
hesaplayınız.
√
1−x−3
√
a) lim
x→−8
2+ 3x
√
√
b) lim
ex + 1 − ex − 1
x→∞
√
(1 − 1 − 4x2 ) sin x
c) lim
x→0
x3
√
(1 − 1 − 4x2 ) sin x
d) lim
x→0
x3
2
x + 2x − 3
e) lim 2
x→1 x + x − 2
|3x − 1| − |3x + 1|
f) lim
x→0
x
p
g) lim
x3 − x
x→0−
p
h) lim
x3 − x
20) Türevin tanımını kullanarak f (x) = x|x| fonksiyonu için f 0 (0) değerini bulunuz.
21) y 4 − 2x2 y 3 − 27 = 0 eğrisinin (−1, 3) noktasındaki
teğet denklemini bulunuz.
√
22) 5 1, 3 ≈?
23) x2 +2y 2 = 1 eğrisine teğet olan ve aşağıdaki şartları
sağlayan doğruların denklemlerini bulunuz.
a) (3, 0) noktasından geçen;
b) y = x doğrusuna paralel olan.
x→0+
(1 + x)(1 + 2x) − 1
x→0
x
i) lim
2