Kullanılan Alet-Malzemeler: a) DC güç kaynağı b) Multimetre c
advertisement

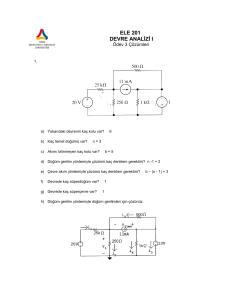
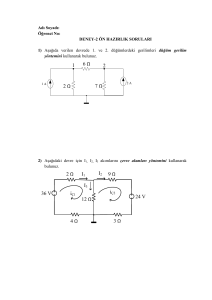
DENEY-4 WHEATSTONE KÖPRÜSÜ VE DÜĞÜM GERİLİMLERİ YÖNTEMİ Deneyin Amacı: Wheatson köprüsünün anlaşılması, düğüm gerilimi ile dal gerilimi arasındaki ilişkinin incelenmesi. Kullanılan Alet-Malzemeler: a) DC güç kaynağı b) Multimetre c) Değişik değerlerde direnç ve bağlantı kabloları 4. Teorik Bilgiler 4.1. Wheatstone Köprüsü Wheatstone Köprüsü aynı giriş gerilimine sahip iki gerilim bölücü devreden oluşur (Şekil 4.1). R1 ve R2 dirençlerinin bulunduğu kısım birinci gerilim bölücü devre, R3 ve R4 dirençlerinin olduğu kısım ise ikinci gerilim bölücü devredir. R1 I3 I1 R3 A Vi A R2 B I5 I2 R4 I4 Şekil 4.1 Wheatstone köprü devresi. Şekil 4.1`de gösterilmiş olan A ve B noktalarının potansiyelleri aynı (VA=VB) ise A ve B noktalan arasındaki potansiyel farkı VA-VB=0 olur. Bu iki nokta arasındaki potansiyel farkının sıfır olması I5 akımının sıfır olmasına neden olur. Devrenin A ve B noktalarının potansiyel değerleri sırası ile VA= [ VB= [ R4 ]Vi R3 R4 R1 R3 R 2 R4 R2 ]Vi R1 R2 olmak kaydıyla VA=VB denge şartı için ; (4.1) elde edilir. Wheatstone köprü devresi hem endüstriyel hem de bilimsel kullanım alanına sahiptir. En yaygın kullanıldığı yer, bilinmeyen dirençlerin belirlenmesidir. Eğer devredeki dirençlerden üçü biliniyorsa, bilinmeyen dördüncü direncin değeri (4.1) bağıntısından kolayca belirlenebilir. Burada bilinmeyen direnç, herhangi bir fiziksel olay sonucunda direnci değişen bir algılayıcı (sensör) olabilir. Örnek olarak bir sensörün direnci, üzerine düşen ışık şiddeti ile sensörün bulunduğu ortamın sıcaklığı ile veya sensör üzerine uygulanan kuvvet ile değişebilir. Böyle bir direnç değişimi sonucunda I5 akımının değişeceği söylenebilir. Böylece, I5 akımının değişim ölçüsü, sensör üzerindeki fiziksel etkinin değişim ölçüsüne özdeş olacaktır. 4.2. Düğüm Gerilimleri Yöntemi Devre çözümlerinde Ohm Yasası ve Kirchhoff Yasaları birlikte kullanılabilir. Fakat daha karışık devrelerde bu yasaların kullanımı zorlaşmaktadır. Karmaşık devreleri çözmek için düğüm gerilimi yöntemini etkili bir yöntem olarak kullanabiliriz. Düğüm gerilimleri yönteminde devrenin düğümlerinden birisi referans düğümü seçilerek diğer bütün düğümlerin bu referans düğümüne göre gerilimlerinin(düğüm gerilimleri) bulunması amaçlanır. Dal gerilimleri ve akımlarıyla düğüm gerilimleri arasındaki ilişki Şekil 4.2 ile açıklanmıştır. 1 R3 2 R5 R2 R1 R4 Vy Vx 0 Şekil 4.2: Düğüm Gerilimi Yöntemi Göstermek İçin Kullanılan Devre Düğüm gerilimleri yöntemi aşağıdaki basamakları içerir: Devredeki düğüm sayısı bulunur. Devredeki düğümlerden bir tanesi (en çok devre elemanının bağlandığı düğüm) referans olarak seçilir ve diğer düğümler adlandırılır. Referans düğüm dışındaki düğümlere Kirchoff Akım Yasası (KAY) uygulanır. Akım yönü keyfi olarak seçilebilir fakat akım yönleri düğümden çıkıyormuş gibi farz edilmesi daha uygundur. Elde edilen düğüm gerilim denklemleri çözülür. 2 Şekil 4.2’deki devreye yukarıda verilen adımlara göre Düğüm Gerilimleri yöntemi uygulanırsa, devrede 3 adet düğüm olduğu görülebilir. 0 ile adlandırılan düğüm referans düğüm olarak seçilmiştir, bu yüzden bu düğüm topraklanmıştır. 1. ve 2. düğümlerin gerilimlerine V1 ve V2 denir ve bu düğümlere KAY uygulanırsa (4.1) ve (4.2) denklemleri elde edilebilir. 𝑉1 𝑉1 − 𝑉𝑥 𝑉1 − 𝑉2 + + =0 𝑅1 𝑅2 𝑅3 (4.1) 𝑉2 − 𝑉1 𝑉2 𝑉2 + 𝑉𝑦 + + =0 𝑅3 𝑅4 𝑅5 (4.2) Burada VX ve Vy değeri bilinen gerilim kaynaklarıdır, denklemler yazılırken bu gerilim kaynaklarının kutuplarının konumlarının dikkate alınması önemlidir. (4.1) ve (4.2) denklemleri yeniden düzenlenirse, aşağıdaki denklemler elde edilir. 𝑉𝑥 (1⁄𝑅 + 1⁄𝑅 + 1⁄𝑅 )𝑉1 + (−1⁄𝑅 )𝑉2 = 1 2 3 3 𝑅2 −𝑉 𝑦 (− 1⁄𝑅 )𝑉1 + (1⁄𝑅 + 1⁄𝑅 + 1⁄𝑅 )𝑉2 = 3 3 4 5 𝑅5 (4.3) (4.4) (4.3) ve (4.4) denklemleri matris formatında şu şekilde ifade edilebilir. 1⁄ + 1⁄ + 1⁄ 𝑅1 𝑅2 𝑅3 [ 1 − ⁄𝑅 3 𝑉𝑥 −1⁄ 𝑅3 𝑉1 𝑅2 ] [ ]=[−𝑉𝑦 ] 1⁄ + 1⁄ + 1⁄ 𝑉2 𝑅3 𝑅4 𝑅5 𝑅5 (4.4) Daha sonra (4.4) sistemi çözülerek (örneğin Cramer yöntemi ile) V1 ve V2 gerilimleri bulunabilir. Deneyin Yapılışı 1. Şekil 4.3 de verilen devreyi kurunuz. Gerilim kaynağının ve ölçüm aletlerinin kutuplarının doğru bağlandığını ve ölçüm aletlerinin doğru aralıklarda seçildiğini kontrol ediniz. 2. Voltmetreyi kullanarak giriş voltajını VE= 5 V a ayarlayınız. Dengesiz durumdaki VCD voltajını ölçünüz.(multimetrenin + kutbunu C noktasına ve - kutbunu D noktasına bağlayınız.) ve ölçülen değerleri kaydediniz. 3. Şekil 4.4 de verilen devreyi kurunuz. Voltmetreyi kullanarak giriş voltajını VE= 5 V a ayarlayınız. Potansiyometreyi dengesiz durumdaki voltajı 0 V olacak şekilde ayarlayınız. (Ayarlama boyunca giriş voltajı 5 V’tan saptıysa tekrar ayarlayınız.) 3 4. Potansiyometreyi devreden iki köprü bağlantı kullanıp ayırarak R4 direnç değerini multimetreyi kullanarak ölçünüz. Şekil 4.3 Wheatstone köprüsü dengesiz durumda voltajının ölçülmesi. Şekil 4.4 Wheatstone köprüsü dengesiz voltajının iptal edilmesi; bir potansiyometre ve üç sabit direnç ile birleştirilmesi 5. Şekil 4.2’deki devreyi seçtiğiniz dirençler ve iki farklı gerilim değeri (Vx ve Vy) için kurarak, V1 ve V2 gerilimlerini ölçünüz. Bulduğunuz değerleri Tablo 4.1’ye kaydediniz. Tablo 4.1: Uygulama 1 Vx-1 Vy-1 Ölçülen1 Hesaplanan1 V1-1 V2-1 4 Bağıl Hata1 6. Bir önceki basamakta kullandığınız gerilim seviyelerini iki katına çıkararak, Vx ve Vy gerilimlerinin yeni değerlerini Tablo 4.2’e kaydediniz ve V1 ve V2 gerilimlerini ölçerek deneyi sonlandırınız. Tablo 4.2: Uygulama 2 Vx-2: Vy-2: Ölçülen2 Hesaplanan2 Bağıl Hata2 V1-2 V2-2 Çalışma Soruları 1. Aşağıdaki şekilde gösterilen devrede wheatstone köprüsündeki galvanometre üzerindeki akım değerini bulunuz. (Cevap: 64 mA) 2. Aşağıdaki şekilde gösterilen devrede düğüm gerilimleri metodunu kullanarak v ve i değerini bulunuz. (Cevap: v= −0.2 V, i= 1.4 A) 5