17 Kasım 2009
Elektrik Devre Temelleri
UYGULAMA-7
Küçük İşaret Analizi
LineerleştirilmişTanım Bağıntıları
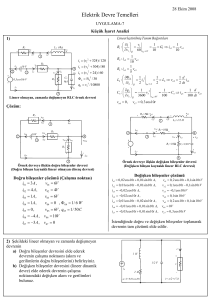
1)
R3
L4 (Φ4)
v3
i3
i6
2
3
v4
i4
1
v2
10 V
⎛ ∂i ⎞
v
1
1
R1 : ⎜ 1 ⎟ = 1
=
= G1 ⇒ ia1 = va1
v
∂
60
10
10
v01 = 6V
⎝ 1 ⎠Q
i1 = (v12 + 324) /120
R2
i2
i1
v1
C5
(q5)
R1
0,3cos10t V
4
v5
i2 = (v2 2 + 304) / 80
i3 = (v32 + 24) / 60
Φ 4 = 5i43 / 30
i7
i5
q5 = v53 /10800
5
Lineer olmayan, zamanla değişmeyen RLC örnek devresi
Çözüm:
R3
2
⎛ ∂q ⎞
1
1
1 d
=
= C5 ⇒ ia 5 =
C5 : ⎜ 5 ⎟ =
v52
va 5
∂
v
dt
3600
100
100
v05 = 6V
⎝ 5 ⎠Q
va 6 = 0,
va 7 = 0,3cos10t
10V
3
va4
R3=5Ω va3
v03
ia3
i03
i06
1
va 2
10
1
R3 : ia 3 = va 3
5
⎛ ∂Φ 4 ⎞
1 2
1
1 d
L4 : ⎜
ia 4
= = L4 ⇒ va 4 =
⎟ = i4
i
∂
2
2
2 dt
i04 =1 A
⎝ 4 ⎠Q
R2 : ia 2 =
R2
v02
i02
1
i04
1
2
v01
i01
L4=1/2 H
va2 R =10Ω
2
ia6
4
v05
ia4
3
ia2
va1
ia1
R1=10Ω
R1
C5=0,01F
ia7
i07
ia5
i05
5
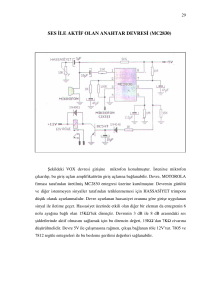
Örnek devreye ilişkin doğru bileşenler devresi
(Doğru bileşen kaynaklı lineer olmayan direnç devresi)
Doğru bileşenler çözümü (Çalışma noktası)
i01 = 3 A ,
v01 = 6V
i02 = 4 A ,
v02 = 4V
i03 = 1A ,
v03 = 6V
i04 = 1A ,
v04 = 0 , Φ 04 = 1/ 6 W
i05 = 0,
v05 = 6V , q05 = 1/ 50 C
i06 = −4 A ,
v06 = 10V
i07 = −3 A ,
v07 = 0
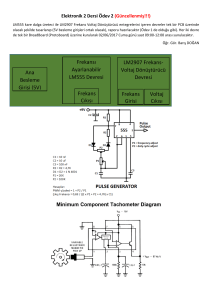
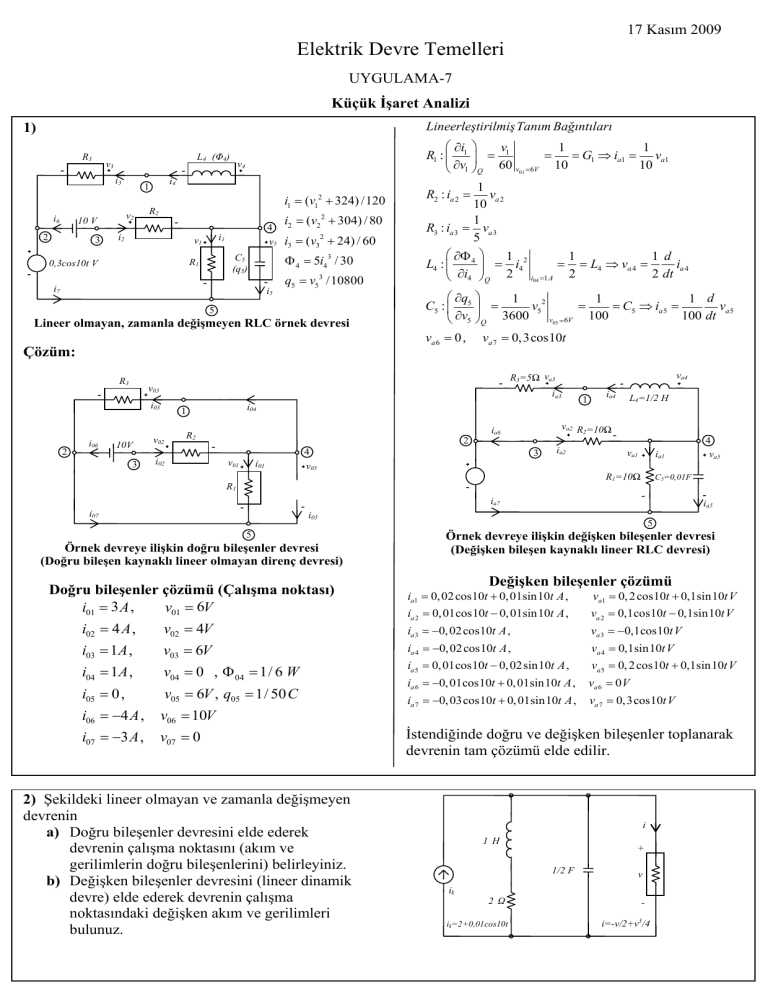
2) Şekildeki lineer olmayan ve zamanla değişmeyen
devrenin
a) Doğru bileşenler devresini elde ederek
devrenin çalışma noktasını (akım ve
gerilimlerin doğru bileşenlerini) belirleyiniz.
b) Değişken bileşenler devresini (lineer dinamik
devre) elde ederek devrenin çalışma
noktasındaki değişken akım ve gerilimleri
bulunuz.
4
va5
5
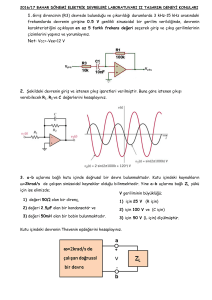
Örnek devreye ilişkin değişken bileşenler devresi
(Değişken bileşen kaynaklı lineer RLC devresi)
Değişken bileşenler çözümü
ia1 = 0, 02 cos10t + 0, 01sin10t A ,
va1 = 0, 2 cos10t + 0,1sin10tV
ia 2 = 0, 01cos10t − 0, 01sin10t A ,
va 2 = 0,1cos10t − 0,1sin10tV
ia 3 = −0, 02 cos10t A ,
va 3 = −0,1cos10tV
ia 4 = −0, 02 cos10t A ,
va 4 = 0,1sin10tV
ia 5 = 0, 01cos10t − 0, 02sin10t A ,
va 5 = 0, 2 cos10t + 0,1sin10t V
ia 6 = −0, 01cos10t + 0, 01sin10t A ,
va 6 = 0 V
ia 7 = −0, 03cos10t + 0, 01sin10t A ,
va 7 = 0,3cos10tV
İstendiğinde doğru ve değişken bileşenler toplanarak
devrenin tam çözümü elde edilir.
i
1 H
+
1/2 F
v
ik
2 Ω
ik=2+0,01cos10t
i=-v/2+v3/4