İNTEGRAL - 6
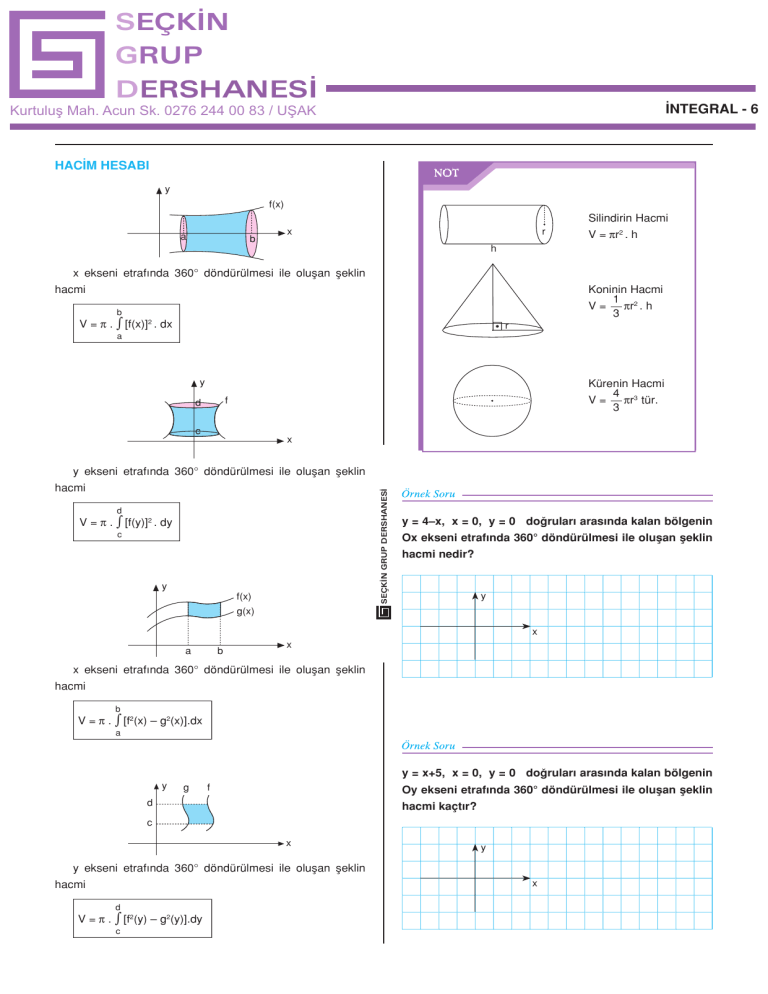
HACİM HESABI
y
f(x)
a
b
x
r
h
SilindirinHacmi
V=πr2 .h
x ekseni etrafında 360° döndürülmesi ile oluşan şeklin
KonininHacmi
1 2
πr .h
V=
3
hacmi
b
V=π. ∫ [f(x)]2 .dx
r
a
y
KüreninHacmi
4 3
πr tür.
V=
3
f
d
c
x
y ekseni etrafında 360° döndürülmesi ile oluşan şeklin
hacmi
d
V=π. ∫ [f(y)]2 .dy
c
y
f(x)
g(x)
a
b
y = 4–x, x = 0, y = 0 doğruları arasında kalan bölgenin
Ox ekseni etrafında 360° döndürülmesi ile oluşan şeklin
hacmi nedir?
y
x
x
x ekseni etrafında 360° döndürülmesi ile oluşan şeklin
hacmi
b
V=π. ∫ [f2(x) – g2(x)].dx
a
y
y = x+5, x = 0, y = 0 doğruları arasında kalan bölgenin
g
f
Oy ekseni etrafında 360° döndürülmesi ile oluşan şeklin
d
hacmi kaçtır?
c
x
y
y ekseni etrafında 360° döndürülmesi ile oluşan şeklin
x
hacmi
d
V=π. ∫ [f2(y) – g2(y)].dy
c
y = x2+3 eğrisi x = 1 doğrusu ve eksenler arasında kalan
y = �x eğrisi ile y = x2 parabolü arasında kalan bölgenin
bölgenin Ox ekseni etrafında 360° döndürülmesi ile olu-
Ox eksenine etrafında 360° döndürülmesi ile oluşan şek-
şan şeklin hacmi kaçtır?
lin hacmi kaç π br3 tür?
y
y
x
x
x = �9–y2 ve |y| = 3–x fonksiyon grafikleri arasında ka-
Oy ekseni etrafında 360° döndürülmesi ile oluşan şeklin
hacmi kaçtır?
y
x
lan bölgenin Oy ekseni etrafında 360° döndürülmesi ile
y = lnx eğrisi y = 2 ve eksenler arasında kalan bölgenin
oluşan şeklin hacmi kaç π br3 tür?
y
x
(2012-LYS)
y
y2 = 1–x parabolü x = 0 ve y = 0 doğruları arasında kalan
3
bölgenin Oy ekseni etrafında döndürülmesi ile oluşan
şeklin hacmi kaç π br tür?
3
1
y
x
1
Birincibölgede;yekseni,y=1doğrusuve9x2 + y2=9elipsi
x
arasındakalanbölgeyeksenietrafında360°döndürülüyor.
Oluşan dönel cismin hacmi kaç br3 tür?
A)
8π
9
B)
10π
9
C)
19π
18
D)
25π
27
E)
28π
27
UYGULAMA TESTİ - 1
6.
y
1.
20
2
4
8
∫
x.y = 2
0
x
A) ln2
D) 2ln2
B) 110
C) 120
D) 140
B) 1 + ln2
C) f(x).dx integralinin değeri kaçtır? A) 100
x
2
Şekilde taralı bölgenin alanı kaç br2 dir?
f fonksiyon grafiği verilmiştir.
–2
1
–2
8
y = 2x
f
10
y
E) 1
ln2
1
+2ln2 ln2
E) 160
7. y = x2 ve y = 16 – x2
2. y = (x – 2)2 parabolü ile eksenler arasında kalan bölgenin alanı kaç br2 dir?
B) 1
C) 2
D) 3
7
3
3. x = 4y – y2 ile y ekseni arasında kalan bölgenin alanı
kaç br2 dir?
A) 5
3
8
B) 3
16
C) 3
20
D) 3
A) 8
E) 3
32
E) 3
A) 4
eğrileri arasında kalan bölgenin alanı kaç br2 dir?
64�3
B) 3
32�3
3
128�3
D) 3
8.
y
4. y = e fonksiyonu x = 1 doğrusu ve eksenler arasında kalan bölgenin alanı kaçtır?
2x
A) e–1
2
e
B) 2
2
C) e2–1
e –1
D) 2
2
y = (x–4)2
x
4
Şekildeki y = x2 ve y = (x – 4)2 eğrileri arasında kalan
bölgenin alanı kaç br2 dir?
A) E) e
8
B) 3
4
3
16
C) 4
D) 3
y
9.
5.
E) 64�3 y = x2
0
76�3
C) 3
y
–6
S1
–2
0
4
S3
8
x
S2
0
m
x
f(x) = sin2x fonksiyonunun grafiği verilmiştir.
Taralı alan
A) 0
19
E) 3
1
br2 olduğuna göre m kaçtır? 2
π
π
π
π
C) D) E) B) 4
6
2
3
Şekilde S1 =
8
∫
–6
S3
S
= 2 = 4 ise,
2
3
f(x).dx integralinin değeri kaçtır? A) 0
B) 3
C) 5
D) 7
E) 8
UYGULAMA TESTİ - 1
10.
�2
2
∫
0
π
B) π
C) 2
�3
�4 – x2 – x . dx �3
0
integralinin değeri kaçtır? ∫
A) 2
�8y –y2 . dy integralinin değeri kaçtır? A) 2π
11.
y
15.
π
3
2π
B) 3
π
D) 4
–2
0
x
2
Yukarıdaki taralı bölgenin Ox ekseni etrafında 360°
döndürülmesiyle oluşan katı cismin hacmi kaç π br3
tür?
π
C) 4
12.
π
E) 8
3π
D) 4
A) 32
B) 3
64
3
16
C) 3
8
D) 3
4
E) 3
π
E) 2
y
16
eğrisi ile y = x, x = 0 ve y = 4
x
eğrileri arasında kalan bölgenin y ekseni etrafında
döndürülmesi ile oluşan cismin hacmi kaç π br3 tür?
16. y =
–4
4
Yukarıdaki şekilde yarım dairenin alanı aşağıdakilerden hangisinde doğru ifade edilmiştir?
A)
C)
2
∫
–2
4
∫
–4
�8 – x2 . dx
B)
�16 – x2 . dx D)
E)
0
∫
–4
4
∫
–4
4
∫
0
�4 – x2 . dx
40
3
44
B) 3
8
3
16
B) 3
17.
�16 – x2 . dx
32
C) 3
64
D) 3
128
E) 3
y
y = x3
y = x
50
C) 3
x
doğruları arasında kalan bölgenin Ox ekseni etrafında 360° döndürülmesiyle oluşan cismin hacmi kaç π
br3 tür?
A) A) �16 – x2 . dx
13. y = 6 – x, y = 0, y = 2, x = 0
x
56
D) 3
Şekilde verilen taralı bölgenin Ox ekseni etrafında
döndürülmesiyle oluşan katı cismin hacmi kaç π br3
tür?
64
E) 3
A) 2
21
3
B) 21
4
C) 21
5
D) 21
6
E) 21
14. y = x2 + 1, parabolü ile x = 2, x = 0, y = 0
doğruları arasında kalan bölgenin Ox ekseni etrafında 360° döndürülmesi ile elde edilen cismin hacmi
kaç π br3 tür?
A) 202
15
203
B) 16
204
C) 15
206
D) 15
207
E) 15
1
2
3
4
5
6
7
8
9
10
D
E
E
D
C
E
D
D
A
B
11
12
13
14
15
16
17
B
C
D
C
B
D
C
İNTEGRAL - 7
Bazı Önemli Fonksiyonların Grafikleri:
y
3.
y
y = mx2
4.
y
y = mx3
x
Taralı Alan =
y
y
2
b
∫ f(y).dy
f
y
|a>1|
1
1
0<a<1
x
x
y
y
y = lnx
� y = �a2–x2
–a
x
1
y
π
π/2
1.
0
x
a
π/2 π
x
y
f(x)
a
Taralı Alan =
b
b
∫ f(x).dx
a
a
∫ f(y).dy
Taralı Alan = –
a
g
f
f
b
∫ f(y).dy
a
b
a
x
x
Taralı Alan
Taralı Alan
=
y
g
a
b
∫ [f(y) – g(y)].dy
=–
a
b
∫ [f(y) – g(y)].dy
a
f(x)
y = cosx
x
a
y
2.
b
b
1
y
d
S1
S3
b
S2
∫ f(x).dx = S1 – S2 + S3 dür.
b
x
f(x)
x
Taralı Alan = –
x
f
y
1
y = sinx
g
x
b
y
1
b
y = ax
y = ax
∫ f(y).dy
a
a
g
Taralı Alan =
b
y
6.
a
y
Taralı Alan = –
a
y.x = m
x
x
f(y) = x
y
5.
x = my
x
f(y) = x
x
x
y
b
∫ f(x).dx
a
a
c
d
x
y = x2 eğrisi ile x = 1 ve x = 3 doğruları arasında kalan
f(x) = lnx eğrisi x = 1 ve x = e3 doğruları arasında kalan
bölgenin alanı nedir?
bölgenin alanı nedir?
y
y
x
x
y = ex, x = 1 ve x = 3 doğruları ile sınırlı kalan bölgenin
y
x
alanı kaçtır?
π
π
,x= ve y = 0 doğruları arasında
3
2
kalan bölgenin alanı nedir?
y = sinx eğrisi ile x =
y
x
y2 = x eğrisi x = 4 doğrusu ve eksenleri arasında kalan
f(x) = 2x eğrisi y = 2 doğrusu ve y ekseni arasında kalan
bölgenin alanı kaçtır?
bölgenin alanı kaçtır?
y
y
x
x
y = 2x2 ve y = x+3 arasında kalan bölgenin alanı kaçtır?
y
S1
–6
–2
4
S2
S3
8
y
x
x
S
S
S1 = 3 = 2 = 5
2
2
8
∫ f(x).dxintegralinin değeri kaçtır?
–6
y = x+3 doğrusu x = 3y–y2 eğrileri arasında kalan bölgenin alanı kaçtır?
(2012-LYS)
Birincibölgedekoordinateksenlerix=5,y=5doğrularıve
y = x2+1,x=y2+1eğrileriarasındakalanAbölgesiaşağıda
verilmiştir.
y
(2,5)
A
x
A bölgesinin alanı kaç birim karedir?
27
2
B)
35
3
x
(5,2)
0
A)
y
C)
43
3
D)
y
71
6
E)
77
6
y=3x2
y=
e
y = x2 ve y2 = 8x eğrileri arasında kalan bölgenin alanı
kaçtır?
y
x
Şekilde verilen taralı alan kaç birimdir?
x
4
x
y
y=
2
5
x
∫ (�4–x2–1).dxintegralinin sonucu kaçtır?
y = 5x
2
–2
x
y
Şekilde verilen taralı bölgenin alan kaç birimdir?
x
4
∫ (�16–x2+x–4).dxintegralinin sonucu kaçtır?
4
∫ �16–x2.dxintegralinin sonucu kaçtır?
0
y
0
y
x
x
f(x) =
�2
∫ (�4–x2–x).dxintegralinin sonucu kaçtır?
x+2,
x<0
x –4x+4,x≥0
2
fonksiyonunun grafiği ve x ekseni arasında kalan bölgenin alanı kaçtır?
0
y
y
x
x
