3.
Test 1’in Çözümleri
E1
1.
30
°
21
1
Elektriksel Alan ve Potansiyel
30° E
2
2d
d
E1
E2
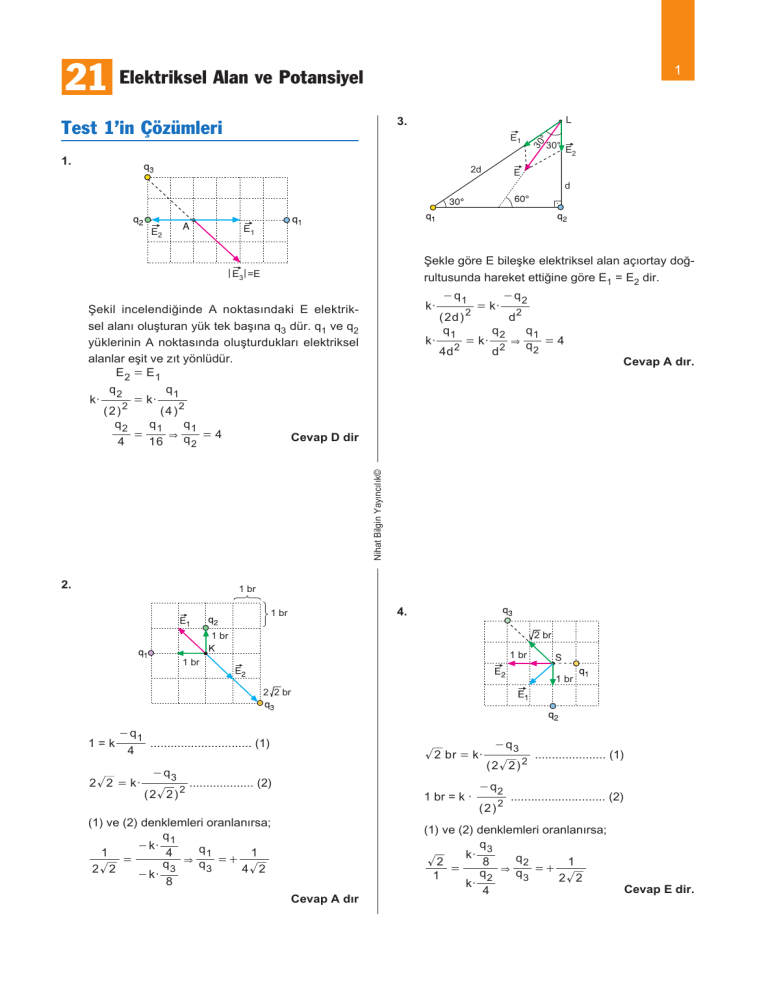
Şekle göre E bileşke elektriksel alan açıortay doğrultusunda hareket ettiğine göre E1 = E2 dir.
| E3 | =E
Şekil incelendiğinde A noktasındaki E elektriksel alanı oluşturan yük tek başına q3 dür. q1 ve q2
yüklerinin A noktasında oluşturdukları elektriksel
alanlar eşit ve zıt yönlüdür.
E2 = E1
q2
q1
= k·
k·
2
(2)
(4)2
q2
q1
q1
=
& q =4
Cevap D dir
4
16
k·
- q1
= k·
( 2d ) 2
q1
= k·
k·
4d2
- q2
d2
q2
q1
& q =4
2
d2
Cevap A dır.
Nihat Bilgin Yayıncılık©
2
2.
1 br
4.
1 br
2 br
1 br
1 br
1 br
1 br
2 2 br
1=k
- q1
4
2 2 = k·
.............................. (1)
2 br = k ·
- q3
(2 2)2
................... (2)
(1) ve (2) denklemleri oranlanırsa;
q1
- k·
q1
1
4
1
=
& q =+
q
3
3
2 2
4
2
- k·
8
(2 2)2
- q2
..................... (1)
1 br = k ·
(1) ve (2) denklemleri oranlanırsa;
q3
k·
q2
2
8
1
=
q2 & q3 = + 2 2
1
k·
4
Cevap A dır
- q3
(2)2
............................ (2)
Cevap E dir.
2
ELEKTRİKSEL ALAN VE POTANSİYEL
5.
7.
q
E=k.––2
d
q
3k.––2
d
q
E=k.––2
d
q
+1
2E=2k.––2
d
O
q
E=k.––2
d
Cevap C dir
• X noktası kürelerin merkezi olduğundan elektrik alan şiddeti EX = 0 dır.
• Küre merkezinden d kadar uzaktaki Y noktaq
sında elektrik alan E Y = k ·
dir.
d2
• Z noktasındaki elektrik alanı bulmak için yükleri kürenin merkezinde toplanmış gibi düşünmeliyiz. Toplam yük;
qT = +q –q = 0
bulunur. Bu nedenle elektriksel alan sıfırdır.
Cevap D dir
6.
8.
E
EA
Nihat Bilgin Yayıncılık©
E
1 br
EA = E 2
qX
2q
= k·
k·
· 2
2
(2)
(2 2)2
- qX
q
= 2 2 · & qX = - 2 q
4
8
1 br
1 br
E 2
qX
Cevap D dir
2 br
2 br
2 br
2 br = k ·
2 br = k ·
q3
(2 2)2
- q2
(2 2)2
.................. (1)
q·E
9.tan 37 ° = m · g
.................. (2)
(1) ve (2) denklemlerinin eşitliğinden;
q3
q3 = –q2 & q = - 1
2
q·3
3
=
4
4 · 10 – 3 · 10
q = 1·10
–2
q
q.E
C
m.g
Cevap A dır.
Cevap A dır
ELEKTRİKSEL ALAN VE POTANSİYEL
10.
+q
12.
+q
K
d
––
2
q2 = q
30°
FK
d
d
––
2
E2
3
q1 = –q
E1
2d
60° 60°
L
(+q)
60°
q2
k . –––
4d2
60° 60°
q2
k . –––
4d2
60°
q2
k . –––
4d2
L noktasındaki +q yükünün dengede kalabilmesi
için;
- k ·
qK
d2
= k·
qK = -
q2
4d2
q2
4d2
q1
= k·
q2
& - q1 = q2 = q
d
d2
bulunur. K noktasında oluşan elektrik alan;
El = E 1 + E 2
q
q
El = k
+ k·
d
d
( )2
( )2
2
2
4q
4q
El = k ·
+ k·
= 8E
d2
d2
Cevap D dır
2
1
q
4
olmalıdır.
Cevap A dır
Nihat Bilgin Yayıncılık©
FK = k ·
- k·
13.
E1
E1,2
E2
11.
q
E = k . ––2
d
q2 = +2q
K
q
E = k . ––2
d
2q
2E = k . ––
d2
2q
2E = k . ––
d2
3 2E
A
q1 = –q
Bileşke elektrik alan 3 2 E dir.
Cevap C dir
q1 = –q yükünün A noktasından uzaklığı 1 birim,
q2 = +2q yükünün A noktasından uzaklığı 2 birimdir. Bir noktadaki elektrik alanının büyüklüğü yük
ile doğru, uzaklığın karesi ile ters orantılıdır. Bu
nedenle iki yükün A noktasında oluşturduğu bileşke elektrik alan vektörü şekildeki E 1, 2 dir.
Cevap A dır
4
ELEKTRİKSEL ALAN VE POTANSİYEL
14.
16.
2E
2E
q2
E
q1
E=k
q
d2
2E = k·
................ ( 1 )
q1
Cevap C dir
(1) denklemi (2) denkleminde yerine yazılırsa;
q1
q
2·k·
= k·
& q1 = 8q
2
d
4d2
(1) denklemi (3) denkleminde yerine yazılırsa;
- q2
q
2· k ·
= k·
2
d
d2
q2 = - 2q
bulunur.
Cevap E dir
15.
q3
k . ––
d2
60°
60°
q
k . ––
d2
q
k . ––
d2
q
k . ––
d2
Şekil incelendiğinde A noktasındaki bileşke elektriksel alanın sıfır olması için q3 = –q olmalıdır.
Cevap B dir
Nihat Bilgin Yayıncılık©
.........( 2 )
( 2d ) 2
- q2
............( 3 )
2E = k
d2
A cismine düşeyde q1, yatayda q2 yüklü cisimler kuvvet uygulamaktadır. Bileşke kuvvetin hem
yatay hem de düşey bileşeni olmalıdır. Bu nedenle
bileşke kuvvet III yönünde olamaz.
5
ELEKTRİKSEL ALAN VE POTANSİYEL
3.
Test 2’nin Çözümleri
E3
A
1.
E1+E3
E2
E1
E1 = 2 br
30°
E2 = 1 br
k·
1
=
2
k·
q2
2
(1) ve (2) denklemleri oranlanırsa;
q2
-k
q2
4
2
=
& q = - 2 2 bulunur.
q
1
1
2
k·
2
Cevap E dir
q2
d
1
- q 1 & q 1 = - 2 bulunur.
d2
Cevap A dir
Nihat Bilgin Yayıncılık©
q1
........................ (1)
( 2)2
- q2
................................(2)
2=k
(2)2
2 = k·
2.
4.
B
E3
E1
E
A
P noktasındaki elektrik alan;
q
E = k·
....................................... (1)
d2
R noktasındaki elektrik alan;
( 3q - q )
2q
El = k ·
= k·
............ (2)
2
9d2
( 3d )
bulunur. (1) denklemi (2) denkleminde yerine yazılırsa;
2
El = E bulunur.
9
Cevap B dir
E2
E2
IV
k·
q3
4d
2
= 1 br & k ·
q3
d2
= 4 br
bulunur. Şekil incelendiğinde bileşke IV gibi olur.
Cevap D dir
6
ELEKTRİKSEL ALAN VE POTANSİYEL
7.
+
+
+
+
5 br
+
+
+
1 br
+
+
+
1 br
+
+
x
+
d
+
+
–
5.
+
+
1 br
k
- q2
( 5)2
- q1
k
(2)2
- q1 · 5
- q2
q1
4
& q =
=
5
4
2
5 5
5
=
1
• S anahtarı kapatıldığında K küresinin yük miktarı değişmeyeceğinden EA değişmez. I. önerme doğrudur.
• B noktasında elektrik alan, L küresinin yükü
sıfır olacağından azalır. II. önerme doğrudur.
Cevap E dir
Nihat Bilgin Yayıncılık©
Cevap C dir
6.
2 2q
k . –––––– = 2 E
(d 2)2
8.
2E
q
k . –– = E
d2
2E
45°
K
45°
45°
45°
K
45°
q
k . –– = E
d2
2E
( El ) 2 = ( 2 E ) 2 + ( 2 E ) 2 = 4 E &
El = 2 E dir .
Cevap D dir
K ve M bölgelerinde elektrik alan sıfır, L bölgesinde ise bir EL elektrik alanı vardır.
Cevap A dır
ELEKTRİKSEL ALAN VE POTANSİYEL
9.
9q
k . ––– = E
9d2
30°
3q
k . ––– = E
3d2
2d
60°
3d
3q
k . ––– = E
3d2
d
3d
q
k . –– = E
d2
A noktasındaki bileşke elektrik alan sıfırdır.
7
kadarlık kuvvet yayı x2 = 6x kadar uzatır. Yayda
depolanan potansiyel enerji;
1
El = k · ( 6 x ) 2
2
1
El = k · 36 x 2 = 36 E bulunur .
2
Cevap E dir
12. A noktasının potansiyeli sıfır olarak verilmiştir. Bu
durumda q2 = q alındığında q1 = –2q olur.
Cevap A dir
Yüklerin A noktasında oluşturdukları bileşke elektrik alan III yönünde olur.
A
watt
P
i2 ·R
V
10.
=
=
=
=E
amper · metre
i·d
i·d
d
Elektrik alan birimidir.
Cevap C dir
k·
q
k· 2 = 2E
d
2q
=E
(2d)2
Enet
Nihat Bilgin Yayıncılık©
Cevap C dir.
11.
13. q1 ve q2 yüklerinin A noktasında oluşturdukları
potansiyeller sıfır olarak verilmiştir. Buradan;
q2 = 2q alınırsa
q1 = –q alabiliriz.
Yüklerin A da oluşturdukları bileşke elektrik alan
IV yönünde olur.
Enet
Şekil I deki yay sistemi için;
Fyay = Felektrik
q·4q
k·x1 = k·
( 2d ) 2
q
k·
=F
d2
F kadarlık kuvvet yayı x1 = x kadar uzatır. Yayda
1
depolanan potansiyel enerji kx 2 = E bulunur.
2
Şekil II deki yay sistemi için;
Fyay = Felektrik
2q·3q
k·x2 = k·
d2
6q
k·
= 6F
d2
k·
k·
2q
=E
(4d)2
q
= 2E
(2d)2
A
q2 = –2q alınırsa
q1 = q olur.
Bu durumda yüklerin A da oluşturdukları bileşke
elektrik alan II yönünde olur.
A
q
k·
(2d)2
k·
2q
(4d)2
Enet
Cevap C dir.
8
ELEKTRİKSEL ALAN VE POTANSİYEL
14.
v2E
X(q)
bağıntısı ile bulunur. Cismin A dan B ye hareketi esnasında; cisme bir kuvvet etki etmediğinden,
WAB= 0 dır. Bir başka ifadeyle, kuvvetin doğrultusu ile hareketin doğrultusu arasındaki açı 90° dir.
cos90°= 0 olduğundan, WAB= 0 olur.
(+q) yüklü cisim B den C ye elektrik alan doğrultusunda, elektrik kuvvetlerinin etkisinde hareket
eder. Bu aralıkta elektrik kuvvetlerinin yaptığı iş;
WBC= F.3d= qE.3d
WBC= 3 qEd bulunur.
E
O
+1
E
Y(2q)
Z(q)
Cevap B dir.
Cevap C dir.
15.
Nihat Bilgin Yayıncılık©
17.
+1
d
K
q2= –2q
A noktasındaki bileşke elektrik alanı III yönünde
olur.
Cevap C dir.
E
C
3d
A
4d
Fiziksel olarak yapılan iş;
W= F . d . cosα
–q
d
q1 ve q3 yükleri A noktasına konulan +1 yüküne
aynı yönde kuvvet uygular.
+q
v0
L
16.
q1= –2q
q1 ve q2 yüklerinin çok uzaktaki K noktasında oluşturdukları elektrik potansiyeli sıfırdır (VK= 0).
q1 ve q2 yüklerinin L noktasında oluşturdukları toplam elektrik potansiyeli;
- 2q
- 2q
VL = k
+k
d
d
4q
VL = - k
d
dir. (–q) yüklü cismin L noktasında durması için
elektrik kuvvetlerinin yaptığı iş;
W = - q ·( VL - VK)
4q
W = - q ·(- k
- 0)
d
W=k
4q2
d
bulunur. O hâlde cismin fırlatıldığı andaki kinetik
enerjisi de;
Ek = k
B
4q2
dir.
d
Cevap D dir.
9
ELEKTRİKSEL ALAN VE POTANSİYEL
3.
Test 3’ün Çözümleri
T
1.
E2
a a
E1,2
F
F
mg
mg
E1
qE
qE
K anahtarı kapatıldığında;
• Sarkacın ivmesi değişeceğinden denge konumundaki v hızı değişir. Anahtar açık iken ipteki
gerilme kuvvetinin büyüklüğü T, anahtar kapatıldığında Tl olsun. Buradan
•
bulunur. Buna göre V numaralı vektör doğru cevap
olur.
Cevap E dir
T=
F2 + m ( g ) 2
Tl =
F 2 + ( mg + q · E ) 2
eşitliklerini yazabiliriz. Bu bağıntılara göre,
anahtar kapatıldığında T gerilme kuvveti değişir.
•
tan a =
olduğundan α açısı da değişir.
F
mg + q · E
Cevap B dir
Nihat Bilgin Yayıncılık©
q1 yükünün L noktasına uzaklığı q2 yükünün L
noktasına uzaklığının 2 katıdır. L noktasında elektriksel potansiyelin sıfır olabilmesi için q1= 2q2 ve
yüklerin zıt olması gerekir. q1(–) ve q2(+) olarak
alınırsa;
q1
2q2
E1 = k·
= k·
= 1 birim
36
(6)2
q2
q2
= k·
= 2 birim
E 2 = k ·
2
9
(3)
2.
x uzaklığı;
q · V1 = q ·
x=
V2
d2
V1
V2
·x
4. I.
·d2
bağıntısıyla bulunur. x uzaklığını küçültmek için;
• d2 uzaklığı azaltılmalıdır.
• V2 gerilimi arttırılmalıdır.
O hâlde II ve III. önermeler doğrudur.
Cevap C dir
q·E
newton
F
E
=
=
=
coulomb · metre
q·d
q·d
d
II.
q
c·V
coulomb
= c = c =V
farad
III.
joule
q·V
J
= q = q =V
coulomb
Cevap D dir
10
ELEKTRİKSEL ALAN VE POTANSİYEL
5.
7.
E1
E
L (+6q)
K (–q)
q3
A
E2 + E3
q2=+4q
O
r
q1=+q
E1 = k ·
q
d2
3r
yalıtkan
4q
4d
2
+ k·
q3
4d2
= 2 br .......... (2)
Yarıçapı r olan bir kürenin içinde her noktaq
da elektriksel potansiyel sabit olup V = k r dir.
Bu kürenin dışında ve kürenin merkezinden
d kadar uzaktaki bir noktada elektriksel potansiyel
q
V=k
dir.
d
kq
k6q
3 kq
+
=
VA = –
2r
3r
2 r
(1) denklemi (2) denkleminde yerine yazılırsa;
q
d
2
B
2r
= 1 br ................................... (1)
E2 + E3 = k ·
2·( k
A
2r
)=k
q
d
2
+k
q3
4d2
q 3 = - 4 q bulunur .
kq
k6q
kq
+
=5
VB = –
4r
4r
4r
VA
6
=
bulunur .
5
VB
Cevap C dir.
Nihat Bilgin Yayıncılık©
A noktasındaki toplam potansiyel ve +q yükünü
topraktan A noktasına taşımak için yapılan iş;
q
4q
4q
q
VA = k + k
-k
=k
d
2d
2d
d
2
q
W = q · ( VA) = k
bulunur .
d
Cevap C dir.
8.
A(q)
B(2q)
r
O
6.
r
X
r
r
Y
–q
+q
K
r
O
+q
L
VX = k
2q
5 kq
q
+k
=
2r
4r
4r
VY = k
2q
11 kq
q
+k
=
3r
4r
12 r
r
+q
W = q ( VY – VX)
XY
Yükün çember üzerindeki hareketi sonucu uzaklık
değişmediğinden V1 = V2 olur. Buradan;
V1
V2
= 1 bulunur.
Cevap C dir.
W XY = q (
5 kq
11 kq
– 4r )
12 r
W XY = –
2
1 kq
3 r
Cevap A dır.
11
ELEKTRİKSEL ALAN VE POTANSİYEL
9.
+
+
+
+
+
+
+
+
+
K
L
A
B
d
d
d
11.
–
–
–
–
–
–
–
–
–
– – – – – – – – – – –
–q
v0
E
+ + + + + + + + + + + + +
+ –
–q yüklü cisim E alanı içinde yatay atış hareketi
yapıyormuş gibi bir yol izler. Hareket sırasında cismin hızının düşey bileşeni sürekli artacağı için hızı
da artar. Ancak elektrik alanın değeri ve cisme etki
eden kuvvet değişmeyeceğinden ivme de değişmez.
V
Paralel levhalar arasında her yerde elektrik alanın
değeri E olup sabittir.
L levhasına göre A noktasının potansiyeli;
VA = E · 2d
Cevap E dir.
B noktasının potansiyeli;
VB = E · d dir.
VA
VB
= 2 bulunur .
Cevap B dir.
Nihat Bilgin Yayıncılık©
12.
A
50 cm
E=50 N/C
10.
X
30 cm
P
Z
B
+
V
–
C
Yapılan iş, elektriksel potansiyel enerji değişimine
eşittir.
Y
Yükü q olan bir parçacığa F kuvveti uygulanarak d
kadar hareket ettirildiğinde yapılan iş;
F · x = q · VCA
E · q · x = q · VCA
W = F·d·cosα = qEd·cosα
bağıntısı ile bulunur. Bu nedenle X-Y arasında
yapılan iş en büyüktür.
50 · 0,4 = VCA
Cevap D dir.
E · x = VCA
VCA = 20 volt
bulunur.
Cevap C dir.
12
13.
ELEKTRİKSEL ALAN VE POTANSİYEL
K
L
P
m +
bulunur. Aynı bağıntıyı YZ levhaları arasında
uygularsak bu durumda parçacık enerji kaybeder.
Çünkü levhalar bir öncekine göre ters bağlıdır.
R
2d
d
v1
+2q
2m +
v2
+q
YZ arasında;
q . V = Ek2 – Ek1
q . V =
+
+
–
3V
–
4V
1
1
m . 4v2 –
m2
2
2 z
mv2
1
1
= m 4 v 2 – mv z2
2
2
2
vz2 = 3v2
Yapılan iş kinetik enerji değişimine eşit olacağından;
q·V = DEk
v Z = 3 v bulunur .
Cevap D dir.
q·V = Ek
2 q ·3 V = 1 mv 2
1
2
1
2 mv 22
2
q ·4 V =
v1
v2 = 3
bulunur .
15.
Nihat Bilgin Yayıncılık©
Cevap E dir.
14.
X
m v
d
Y
2d
–q
L
d
m
X
–2q
–
2d
m
+
– +
V
2V
Şekil I
Şekil II
Paralel levhalar arasındaki düzgün elektrik alan
içine bırakılan yüklü cisim sabit ivmeli hareket
yapar. Bu ivmenin büyüklüğü;
qE
qV
F
a = m = m =
bulunur.
md
q
+ –
– +
3V
V
Parçacığın hareketi sırasında kazandığı veya kaybettiği enerji kinetik enerji değişimine eşittir. Yani;
qV = ΔEk dir.
a ivmesiyle düzgün hızlanan yüklü cismin t sürede
aldığı x yolu;
1
1 qV 2
·
· t bulunur.
x = at 2 =
2
2 md
Bu bağıntıdaki t2 yi yalnız bırakırsak;
XY arasında;
2 md · x
2 md 2
t 2 =
=
yazabiliriz.
qV
qV
q . 3V = Ek2 – Ek1
Her iki şekil için t bağıntılarını yazalım.
1
1
q . 3V =
m . 4v2 –
mv2
2
2
q . V =
mv 2
2
Y
Z
2v
m
K
t 21 =
2 md 2
= t ise
qV
t 22 =
2m4d2
2 md 2
=
= t olur .
2q2V
qV
Cevap A dır.
ELEKTRİKSEL ALAN VE POTANSİYEL
16.
d
–q
d
d
A
B
C
K
L
M
+q
+
–
V
D
N
– +
2V
A noktasında E kinetik enerjisi ile atılan –q yüklü parçacık, hareketine zıt yönlü sabit bir kuvvetin
etkisinde kalarak B noktasından geri dönüyor. Bu
aralıkta –q yüklü cisme etki eden zıt yönlü kuvvetin yaptığı iş;
W = q · V dir.
K noktasından atılan +q yüklü parçacık L noktasına vardığında kinetik enerjisi 2 katına çıkmış olup
2qV dir. L noktasından sonra yüklü parçacık hareketine ters yönde bir kuvvetin etkisinde kalacağı
için yavaşlar. İkinci aralıkta üretecin potansiyeli 2V
olduğundan parçacık N noktasından geri döner.
Nihat Bilgin Yayıncılık©
Cevap B dır.
13