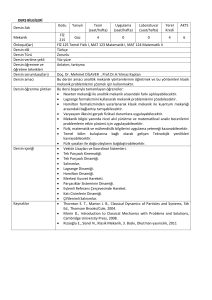
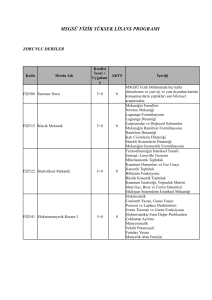
Sistem Dinamiği
Bölüm 5-Blok Diyagramlar, Durum-Değişken Modelleri ve
Simülasyon Metodları
Doç.Dr. Erhan AKDOĞAN
Sunumlarda kullanılan semboller:
El notlarına bkz.
Yorum
Soru
Bolum No.Alt Başlık No.Denklem Sıra No
Denklem numarası
MATLAB
Şekil No
Şekil numarası
Dikkat
Şekil No
Tablo numarası
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131-Sistem Dinamiği
Bölüm 1
2
Bölüm içeriği:
Model formları
Transfer fonksiyonları ve blok diyagram modelleri
Durum-değişken modeli
MATLAB Metodları
MATLAB ile durum değişken metodları
MATLAB ode fonksiyonları
SIMULINK Metodları
Simulink ve Lineer Modeller
Simulink ve Nonlineer Modeller
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131-Sistem Dinamiği
Bölüm
3
GİRİŞ:
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131-Sistem Dinamiği
Bölüm
4
Dinamik modeller farklı formlarda bulunabilir:
Tek eşitlik
1. dereceden eşitlik setleri (Caushy veya durum
değişken formu)
Yüksek dereceden bağlı eşitlikler
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
5
Konu 1: Model Formları
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131-Sistem Dinamiği
Bölüm
6
5.1. Transfer fonksiyonları ve blok diyagram modelleri:
Sistem cevabı zorlanmış ve zorlanmamış cevabın
toplamıdır.
Başlangıç koşulları 0 ise zorlanmamış cevap 0 olur
ve toplam cevap zorlanmış cevaba eşittir.
İlk olarak başlangıç koşullarının 0 olduğunu kabul
ederek çözüm yapacağız.
Transfer Fonksiyonu
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
7
Basit ODE ve Laplace
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
8
Birden fazla giriş durumu:
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
9
Örnek:
X(s)/V(s) ve Y(s)/V(s) bulunuz.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
10
5.1.1. Blok Diyagramlar:
Sistem dinamiklerinin anlaşılmasını kolaylaştıran diyagramlardır.
Verilen bir sistemin transfer fonk. bulmakta da kullanılabilir.
Sistem elemanları
Fiziksel bağlantılar
Bilgilerini içerir
Parametreler
Akış yönü
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
11
5.1.2. Blok diagram sembolleri
Şekil 5.1.1
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
12
5.1.3. Bazı basit blok diyagramlar:
Çarpıcı veya kazanç
İntegratör
Şekil 5.1.2.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
13
5.1.4.Eş değer blok diyagram:
Şekil 5.1.3.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
14
5.1.5. Seri elemanlar ve geri besleme
Şekil 5.1.4.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
15
Geribesleme
Şekil 5.1.4.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
16
5.1.6. Blok diyagramların yeniden düzenlenmesi:
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
17
Şekil 5.1.5
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
18
Önemli hususlar:
Bir transfer fonksiyonu birden fazla şekilde farklı
blok diyagram ile temsil edilebilir.
Bağımlı değişkenin en yüksek dereceli terimi yalnız
bırakılmalı ve sonuç eşitliğinin sağ yanı bir
integratörün girişi olmalı.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
19
Birden fazla giriş ile blok diyagramlar:
Şekil 5.1.6
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
20
5.1.7.Blok diyagramlardan transfer fonk. eldesi
Örnek 5.1.1 Seri bloklar ve çevre indirgeme
Transfer fonksiyonunu bulunuz.
Şekil 5.1.7.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
21
Çözüm 5.1.1.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
22
Şekil 5.1.7
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
23
Örnek 5.1.2.
Sistem modelini belirleyiniz.
Şekil 5.1.2.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
24
Şekil
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
25
5.1.8.MATLAB kullanarak blok diyagram cebiri
Uygulama saati
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
26
5.2. Durum Değişken Modelleri
(State-variable models)
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131-Sistem Dinamiği
Bölüm
27
Durum eşitlikleri:
Birinci derece diferansiyel eşitlikler şeklinde yazılan
formalara durum-değişken formu ve Cauchy formu adı verilir.
Bunları kullanarak yüksek dereceden eşitliklerin dereceleri
indirgenir.
Bu durum analiz ve yazılım açısından daha kolay bir yapıyı
oluşturur.
Bunlar matris yada vektör formlarda gösterilir.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
28
durum değişkenleri
durum eşitlikleri
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
29
Kütle-yay-sönüm sisteminde durum değişkenleri:
5.2.1
Durum değişkenleri
5.2.2
Durum değişken modeli
5.2.3
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
30
Eğer durum değişkenlerini aşağıdaki gibi seçer isek:
Durum değişken modeli:
Durum değişkenlerinin seçimi mutlak ve tek değildir. Ancak seçimler muhakkak birinci
dereceden olmalıdır.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
31
Örnek 5.2.1.
Şekil 5.2.1.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
32
Çözüm 5.2.1.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
33
Çözüm 5.2.1.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
34
5.2.1.Durum değişken modellerinin vektör-matris formu
Vektör-matris notasyonu bize çoklu denklemleri tek bir
matris eşitliğinde göstermemize olanak sağlar.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
35
Örnek 5.2.2. Tek kütle modelinin vektör-matris formu
Yukarıda verilen tek kütle modelini vektör-matris formunda gösteriniz.
Çözüm:
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
36
Örnek 5.2.3.İki kütle modelinin vektör-matris formu
Çözüm:
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
37
5.2.2. Durum eşitliğinin standart formu:
Durum değişeni sayısı: n
Durum değişkenleri: xi
Giriş sayısı: m
Giriş değişkenleri: ui
5.2.9.
Durum vektörü x, n satırlı sütun vektördür.
Sistem matrisi A, n satırlı n sütunlu kare matristir.
Giriş vektörü u, m satırlı sütun vektördür.
Kontrol yada giriş matrisi B, n satırlı m sütunludur.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
38
5.2.3. Çıkış eşitlikleri:
Mesela kütle-yay sisteminde net kuvvet ve momentum ile ilgileniyor isek:
yada
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
39
Çıkış sayısı: p
Durum değişken sayısı: n
Giriş sayısı: m
Giriş sayısı: m
5.2.10
Çıkış vektörü y, p satırlı sütun vektör.
Durum çıkış matrisi C, p satır n sütunludur.
Kontrol çıkış matrisi D, p satırlı m sütunludur.
C ve D matrisleri durum değişkenleri ve girişlerin lineer kombinasyonudur. çıkış bir nonlineer
fonksiyon ise 5.2.10 standart formu uygulanamaz.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
40
Örnek 5.2.4. İki kütle modeli için çıkış eşitliği:
2
Çözüm:
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
41
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
42
5.2.5.Pay dinamiklerine sahip model formları:
Modelin zorlanmamış cevabı ile ilgilendiğimizi düşünelim:
Mesela modelin bu hali ile zorlanmamış sistem cevabı sonraki bölümde
bahsi geçecek olan MATLAB “initial” fonksiyonu ile kolayca elde edilebilir.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
43
Örnek 5.2.5. 1. derece sistemde pay dinamikleri:
(1)
(2)
Yukarıdaki modeli standart formda durum-değişken modeline çeviriniz.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
44
Çözüm 5.2.5. İki yol mevcuttur:
1. yöntem:
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
45
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
46
İkinci yöntem:
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
47
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
48
Tablo 5.2.1.Pay dinamikleri için bir durum-değişken formu:
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
49
Konu 2.
MATLAB ile Durum-Değişken
Metodları
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131-Sistem Dinamiği
Bölüm
50
initial fonksiyonu zorlanmamış yanıtı hesaplar ve
sadece durum-değişken modelinde kullanılır.
MATLAB durum değişken ve transfer fonksiyonu
formları arasında geçiş yapabilir.
5.3.1
5.3.2
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
51
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
52
5.3.1.LTI Nesneleri ve ss(A,B,C,D) Fonksiyonu
ss (state-space)
Bir durum modelinden bir LTI nesnesi oluşturmak
için ss(A,B,C,D) fonksiyonu kullanılır.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
53
ss(sys) ve ssdata(sys) fonksiyonları:
ekran çıktısı
durum denklemleri
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
54
5.3.4. tfdata fonksiyonu:
tfdata, tf fonksiyonu ile tanımlanmış sistemin pay ve paydasını verir.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
55
Örnek 5.3.1.
Örnek 5.2.3’de verilen sistemin durum-değişken modelini elde etmiştik.
X1(s)/F(s) ve X2(s)/F(s) transfer fonksiyonlarını elde ediniz. Buna göre;
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
56
Çözüm 5.3.1.
x1 ve x2 fonksiyonlarının transfer matrislerini istediğimizden
dolayı öncelikli olarak C ve D matrislerini tanımlanması gerekir.
Örnek 5.2.1.den
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
57
Tablo 5.3.1.LTI Nesne Fonksiyonları:
Şekil
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
58
5.3.5. Lineer ODE Çözücüler:
MATLAB Control System Toolbox, lineer modeller için bazı çözücüler
sağlar.
Bunlar giriş fonksiyon çeşidine göre sınıflandırılabilir.
0 giriş
Impuls giriş
Adım giriş
Genel giriş fonksiyonu
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
59
5.3.6. MATLAB “initial” fonksiyonu:
Bu fonksiyon bir durum modelinin zorlanmamış cevabını hesaplar
ve çizer.
Bu MATLAB dokümanlarında bazen initial condition response veya
undriven response olarak da yer alır.
Komut……..
>>initial(sys,x0);
sys: durum değişkeni formunda LTI nesne
x0: başlangıç koşul vektörü
Örnekleme zamanı ve çözüm için alınan nokta sayısı otomatik olarak
ayarlanır.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
60
Örnek 5.3.2.İki kütle modelinin zorlanmamış cevabı:
2
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
61
Çözüm 5.3.2.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
62
5.3.7.impulse, step ve sim fonksiyonları:
step fonksiyonu ile program y çıkış fonksiyonunu ve zaman
vektörü t’yi geri döndürür. [y,t]=step(sys,..). Grafik çizdirilmez.
[y,t,x]=step(sys,…) ile durum uzayı modeli için durum vektör
çözümü elde edilir.
lsim fonksiyonu durum-uzayı modeli ile 0 olmayan başlangıç
koşulları için kullanılır.
>>lsim (sys,u,t,x0)
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
63
Tablo 5.3.2
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
64
Örnek 5.3.3.İki kütle modelinin toplam cevabı:
Eğer iki kütle modelinde giriş 3 genlikli bir step ile zorlanırsa toplam
cevabı bulunuz.
% InitialPlusStep.m
A = [0,0,1,0;0,0,0,1;-1,4/5,-12/5,8/5;4/3,-4/3,8/3,-8/3];
B = [0;0;0;1/3];
C = [1,0,0,0;0,1,0,0];
D = [0;0];
sys = ss(A,B,C,D);
[ystep,t] = step(3*sys);
yfree = initial(sys,[5,1,-3,2],t);
y = yfree + ystep;
plot(t,y),xlabel('t'),gtext('x_1'),gtext('x_2')
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
65
5.3.8.Karakteristik polinomun elde edilmesi:
A matrisi yukarıda verilmiştir. İlgili eşitliği yazınız. İpucu:
Karakteristik denklem aşağıdaki komut satırı ile elde edilir.
Karakteristik kökler roots(poly(A)) komutu ile elde edilir.
Ayrıca A matrisinin eigen değerlerinden, karakteristik denklem kullanılmadan,
karakteristik denklemin kökleri elde edilebilir. Bunun için eig(A) komutu kullanılır.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
66
5.4. MATLAB ode Fonksiyonları
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131-Sistem Dinamiği
Bölüm
67
Lineer ve nonlineer eşitlikler:
Sayfa 279
Bağımsız değişkenlerin nonlineer fonksiyonları nonlineer dif. denklem
üretmez.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
68
5.4.1. Bir çözüm metodunun seçilmesi:
Laplace metodu ve Bölüm 5.3.1. deki durum değişkenli MATLAB
çözüm metodları değişken katsayılı diferansiyel denklemlerin ve
nonlineer eşitliklerin çözümünde kullanılamaz.
Birinci dereceden olmak üzere nonlineer diferansiyel denklemlerin
kapalı formdaki çözümlerinin elde edilmesi için bazen kullanılabilir.
Bunların dışındaki durumlarda çözüm nümerik olarak elde edilmelidir.
Bu bölümde dif. denklemlerin nümerik çözüm metodlarını vereceğiz.
Öncelikli olarak birinci dereceden durumlar göz önüne alınacak daha
sonra ise yüksek dereceli diferansiyel denklemler incelenecektir.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
69
Nümerik metodların temeli dif. denklemin bir fark denklemine
dönüştürülmesidir. Böylece bir bilgisayar tarafından çözülebilecek forma
getirilir.
Nümerik algoritmalar belirli bir algoritmik yapıya sahiptir.
Çözümün doğruluğu, programın karmaşıklığı ile paraleldir.
Önemli olan step size (adım büyüklüğü) ve onun çözümün doğruluğu
üzerindeki etkisinin doğru anlaşılmasıdır.
Bu nedenle en basit metod olan Euler metodu ile başlayacağız.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
70
5.4.2. Euler Metodu:
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
71
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
72
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
73
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
74
Tablo 5.4.1.Bu bölüme ait MATLAB fonksiyonları
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
75
Örnek:
dy/dx=r.y olarak veriliyor.
0<=t<=0.5 aralığında çözüm çizdirilecektir.
r=-10 olarak veriliyor.
y(0)=2 (Başlangıç koşulu)
tao=-1/r=0.1 (Zaman sabiti)
y(t)=2.exp(-10t) olacaktır
deltat=0.02 (zaman sabiti taonun %20’si) seçilmiştir.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
76
2
%Sayfa 281 Euler Metod
1.8
r=-10; delta=0.02;y(1)=2;
k=0;
1.6
for time=[delta:delta:.5]
1.4
k=k+1;
1.2
y
y(k+1)=y(k)+r*y(k)*delta;
1
end
t=(0:delta:0.5);
0.8
y_exact=2*exp(-10*t);
0.6
plot(t,y,'o')
0.4
hold on
0.2
plot(t,y_exact);
0
xlabel('t'),ylabel('y')
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
0
0.05
0.1
MKT3131
Sistem Dinamiği
0.15
0.2
0.25
t
0.3
0.35
0.4
0.45
0.5
77
ode45
Solvers: MATLAB tarafından denklem çözmek için
kullanılan fonksiyonlara verilen isimdir.
ode45, 4. ve 5. derece Runge-Kutta algoritması
tabanlı geliştirilen bir çözücüdür.
Detaylı bilgi için https://www.mathworks.com/help/
matlab/ref/ode45.html
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
78
5.4.3.Çözücü yazım stili:
Tablo 5.4.2. ode45 çözücü temel yazım stili
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
79
Örnek 5.4.1.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
80
Şekil
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
81
5.4.4.Yüksek dereceden eşitliklerin genişletilmesi:
(1)
(2)
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
82
Şekil 5.4.5
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
83
Konu 3: SIMULINK Metodları
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131-Sistem Dinamiği
Bölüm
84
5.5. Simulink ve Lineer Modeller:
Blok yapısı
Veri depolama
Veri çekme
Matematiksel fonksiyonlar ve ihtiyaca uygun toolboxlar.
http://www.mathworks.com/products/?s_tid=gn_ps
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
85
5.5.1 Simulasyon diyagramları
Şekil
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
86
Örnek 5.5.1.
Şekil 5.5.4.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
87
Verinin workspace’e kaydı:
Şekil 5.5.5
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
88
Örnek 5.5.3.
Şekil 5.5.6.
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
89
5.5.2.Durum değişken modellerinin simülasyonu:
Şekil 5.5.7
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
90
Şekil
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
91
5.6.1.Transfer fonksiyon modellerinin simülasyonu:
Kütle-yay-sönüm sistem modeli
Dead-zone
Ölü Bölge
(giriş fonksiyonu ölü
bölgeye maruz kalıyor)
Şekil 5.6.6
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
92
Şekil 5.6.7
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
93
Örnek 5.6.3. Nonlineer pendulumun simulink modeli:
Şekil 5.6.11
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
94
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
95
Şekil 5.6.12
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
96
5.6.2. Araç süspansiyon cevabı:
Şekil 5.6.14
Şekil 5.6.13
Şekil 5.6.15
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
Şekil 5.6.16
MKT3131
Sistem Dinamiği
97
Çözüm:
Sistem modeli:
md2x/dt2=fs+fd
Şekil 5.6.17
Şekil 5.6.18
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
98
Şekil 5.6.19
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
99
Bölüm özeti:
Blok diyagramlar
Durum değişken modelleri
Vektör-matris formu
Yüksek dereceli dif. denklem çözümleri için nümerik
metodlar kullanılır. Bilgisayar programları bu algoritmalar
ile çözüm yapabilir.
MATLAB fonksiyonları(ss, ssdata, tfdata, step, impulse,
lsim, initial, eig)
Simulink
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131
Sistem Dinamiği
100
GELECEK KONU:
Bölüm 6.Elektrik ve
Elektromekanik Sistemler
Doç.Dr. Erhan AKDOĞAN
YTÜ-Mekatronik Mühendisliği
MKT3131-Sistem Dinamiği
Bölüm
101
Referans:
System Dynamics, William Palm III,
McGraw-Hill Education;
3 edition (March 19, 2013)