a .1 .2 .3 .4 .5 .b .c .d .a .1 .2 .3 .4 .5 .b .c .d .a .1 .2 .3
advertisement
FONKSİYONLAR
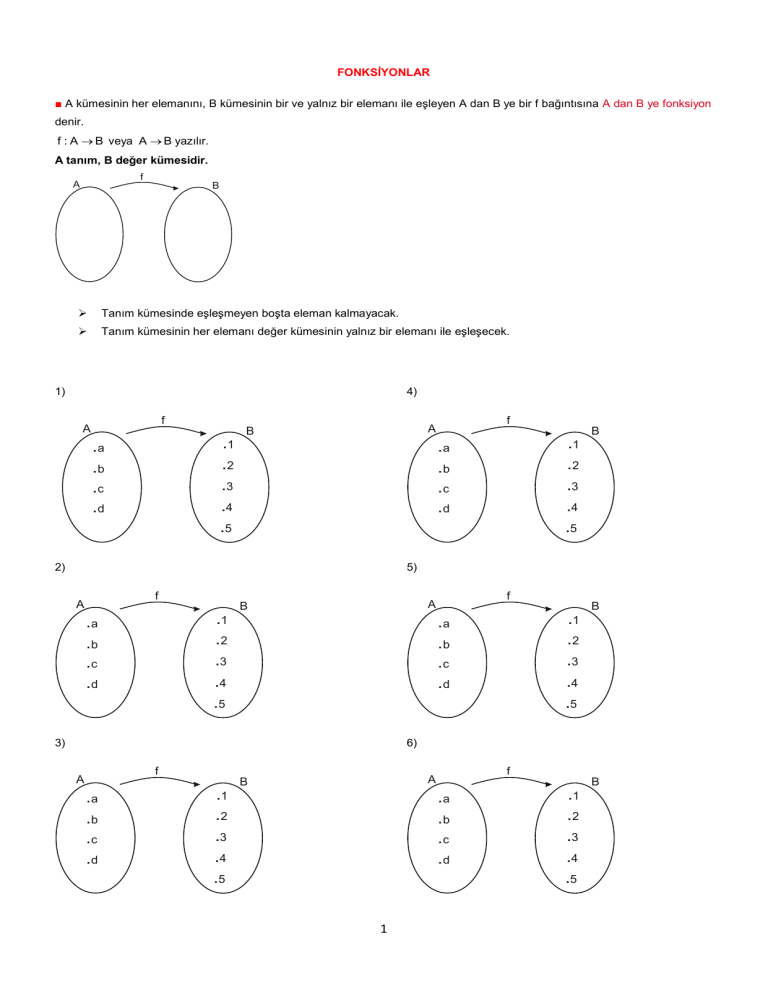
■ A kümesinin her elemanını, B kümesinin bir ve yalnız bir elemanı ile eşleyen A dan B ye bir f bağıntısına A dan B ye fonksiyon
denir.
f : A B veya A B yazılır.
A tanım, B değer kümesidir.
f
A
B
Tanım kümesinde eşleşmeyen boşta eleman kalmayacak.
Tanım kümesinin her elemanı değer kümesinin yalnız bir elemanı ile eşleşecek.
1)
4)
f
A
.1
.2
.3
.4
.5
.a
.b
.c
.d
f
A
B
.1
.2
.3
.4
.5
.a
.b
.c
.d
2)
B
5)
f
A
.1
.2
.3
.4
.5
.a
.b
.c
.d
f
A
B
.1
.2
.3
.4
.5
.a
.b
.c
.d
3)
B
6)
f
A
.a
.b
.c
.d
.1
.2
.3
.4
.5
f
A
B
.a
.b
.c
.d
1
.1
.2
.3
.4
.5
B
www.idealmatematik.com
Fonksiyonlar
Fonksiyonların gösterimi:
4. Örnek:
1. Örnek:
Aşağıdaki bağıntılardan hangisi fonksiyondur?
A = { a, b, c } ve B = { x, y, z, t }
A) f : N → N, f(x) = 3x – 1
B) f : Z → N, f(x)
olduğuna göre, aşağıdaki bağıntılardan hangisi A dan B ye
bir fonksiyondur?
2x 3
5
C) f : Z → N, f(x) 3x 1
A) { ( a, x ), ( c, z ) }
D) f : R → Z, f(x) x 2
B) { ( a, x), ( b, y ), ( c, z ), ( b, t ) }
3
4
2
E) f : Z → N, f(x) = x + 3
C) { ( a, x ), ( b, y), ( c, y ) }
D) { ( a, z ), ( b, t ), ( b, y) }
E) { ( x, a), ( y, b ), ( z, c ), ( t, c) }
5. Örnek:
4
2. Örnek:
2
A = { 1, 2, 3, 4 } ve B = { x, y, z } kümeleri için aşağıdaki
bağıntılardan hangisi B den A ya bir fonksiyon belirtir?
-3
O
3
7
x
-2
A) { (x, 1), (y, 2), (y, 3) }
B) { (x, 2), (y, 3), (z, 1), (z, 4) }
Yukarıda grafiği verilen f fonksiyonunun tanım kümesi
aşağıdakilerden hangisidir?
C) { (x, 3), (z, 4) }
D) { (x,1), (y, 2),(z, 2) }
E) { (1, z), (2, y), (3, x), (4, y) }
A) [–3, 0)
[4,7)
B) (–3, 0)
(3,7]
C) [–3, 2]
(3,7)
D) (–3, 3)
(3,7]
E) [–3, 2)
(4,7]
(2010 – LYS1 – Mat)
3. Örnek:
6. Örnek:
f, A kümesinden B kümesine tanımlı bir fonksiyondur, f nin
şema ile gösterimi aşağıda verilmiştir.
Aşağıdaki grafikleri verilen bağıntılardan hangisi R den R
ye fonksiyondur?
f
A
B
.2
.4
.1
.2
.3
.6
.8
.8
.12
Buna göre, aşağıdakilerden hangisi yanlıştır?
A) f nin tanım kümesi { 2, 4, 6, 8 } dir.
B) f nin değer kümesi { 1, 2, 3, 8, 12 } dir.
C) f nin görüntü kümesi { 1, 2, 8, 12 } dir.
D) f(4) + f(6) = 10
E) f(2) + f(8) = 10
–––––––––––––––––––––––––––––––––––––––––––––––
www.idealmatematik.com
2
www.idealmatematik.com
Fonksiyonlar
Kural: f: A → B ye tanımlı fonksiyon sayısı = [s(B)]
s(A)
dır.
11. Örnek:
7. Örnek:
f : [ – 3, 4 ] → R
A = { a, b, c, d } ve B = { 1, 2, 3 }
f (x) = 2x + 3
kümeleri verildiğine göre, A kümesinden B kümesine kaç
farklı fonksiyon tanımlanabilir?
olduğuna göre, f ([ –3, 4 ]) görüntü kümesi
aşağıdakilerden hangisidir?
A) 3
B) 4
C) 12
D) 64
E) 81
8. Örnek:
C) 135
D) [ 3, 15]
E) [ 3, 19 ]
C) [ 3, 11 ]
f(x) = 4x + 2
B den A ya tanımlanan bağıntılardan kaç tanesi fonksiyon
değildir?
B) 225
B) [ – 3, 11 ]
–––––––––––––––––––––––––––––––––––––––––––––––
12. Örnek:
s(A) = 4 ve s(B) = 2 ise,
A) 240
A) [ – 3, 8 ]
D) 52
olduğuna göre, f(3) + f(1) kaçtır?
E) 14
A) 17
–––––––––––––––––––––––––––––––––––––––––––––––
9. Örnek:
B) 18
C) 19
D) 20
E) 21
13. Örnek:
A = { 1, 3, 5 } kümesinden N ye tanımlı,
f x x 2 x
f(x) = 2x – 3
olduğuna göre, f(–1) + f(0) + f(1) toplamı kaçtır?
fonksiyonunun görüntü kümesindeki elemanların
toplamı kaçtır?
A) 8
B) 9
C) 10
D) 11
A) –4
B) –2
C) 0
D) 2
E) 4
(2003 – ÖSS)
E) 12
14. Örnek:
10. Örnek:
1 2x 2, x 0
2x 1
f(x)
, 0x4
3
3x 1 , x 4
A = { – 1, 0, 1} kümesi veriliyor.
3
f : A → R , f (x) = 3x – 2
fonksiyonu için f(A) kümesi aşağıdakilerden hangisidir?
A) { –2, 1}
B) { – 2, 1, 5 }
D) {1, 2 }
E) { 2, 3 }
www.idealmatematik.com
Buna göre, f(–2) + f(2) + f(5) kaçtır?
C) { –5, –2, 1 }
A) 8
3
B) 10
C) 14
D) 16
E) 18
www.idealmatematik.com
Fonksiyonlar
15. Örnek:
19. Örnek:
Sekiz raftan oluşan bir kitaplığın raflarına 1'den 8'e kadar
numara verilmiştir. Bu kitaplığın t numaralı rafındaki
kitapların sayısını gösteren f fonksiyonu,
f(3x + 1) = 6x + 2
olduğuna göre, f(x) aşağıdakilerden hangisidir?
A) x – 1
t 1, 1 t 4 ise
f t
2t 1, 5 t 8 ise
B) x
C) 2x +1 D) 2x
E) 3x
biçiminde veriliyor.
Buna göre, raflarda toplam kaç kitap vardır?
A) 54
B) 56
C) 58
D) 60
20. Örnek:
E) 62
f(
( 2013 – ALES – ilkbahar )
x2
2x 12
)
x6
3x 6
olduğuna göre, f(x) aşağıdakilerden hangisidir?
16. Örnek:
A)
Rasyonel sayılar kümesinde f, g ve h fonksiyonları
2x
3
B)
3x
2
C)
2
3x
D)
3
2x
E) 2x
3
f(x) = x –x
3
g(x) = 2x +x
h(x) = f(x) + g(x)
biçiminde tanımlanıyor.
–––––––––––––––––––––––––––––––––––––––––––––––
21. Örnek:
h(a) = 24 olduğuna göre, a kaçtır?
3
A) 2
B) 3
C) 4
D)
2
f(3x – 2x + 3) = 6x – 4x + 13
2
E)
4
3
2
olduğuna göre, f(4) kaçtır?
A) 13
( 2012 – ALES – İlkbahar )
–––––––––––––––––––––––––––––––––––––––––––––––
17. Örnek:
B) 15
C) 17
D) 19
E) 21
22. Örnek:
f(x) = 3x + 7
f(4x + 2) = 5x + 3
olduğuna göre, f(2x) – f(x + 1) ifadesi aşağıdakilerden
hangisine eşittir?
olduğuna göre, f(14) kaçtır?
A) 10
A) 3x – 1 B) 3x – 3 C) 5x – 2 D) 5x + 4 E) 5x + 7
B) 12
C) 14
D) 16
E) 18
(2013 – DGS)
23. Örnek:
18. Örnek:
3
x 1
2
f
x x2
x 1
2
f(x) = x – 3x + 3x – 1
olduğuna göre, f(x + 1) değeri nedir?
3
3
3
A) x + 1 B) x – 1 C) x
2
D) x
olduğuna göre, f(3) değeri kaçtır?
2
E) x + 1
A) 5
(1988 – ÖSS)
www.idealmatematik.com
B) 6
C) 7
D) 8
E) 11
(2010 – LYS1 – Mat)
4
www.idealmatematik.com
Fonksiyonlar
24. Örnek:
28. Örnek:
Gerçel sayılar kümesi üzerinde bir f fonksiyonu
f(x – 1) = x . f(x) ve
x
f( 1) 2x a
3
f(21) = 1
olduğuna göre, f(1) kaçtır?
biçiminde tanımlanıyor.
A) 17!
f(4) = 10 olduğuna göre, a kaçtır?
A) 6
B) 8
C) 9
D) 10
B) 18!
C) 19!
D) 20!
E) 21!
E) 12
–––––––––––––––––––––––––––––––––––––––––––––––
Fonksiyonlarda Dört İşlem
25. Örnek:
A ile B ayrık olmayan iki küme olmak üzere,
2
f: R → R,
f : A → R ve g : B → R
2
f(2x – 1, y + 2) = 2x – 3xy + 3
tanımlı f ve g fonksiyonları veriliyor.
olduğuna göre, f(3 , 6) kaçtır?
A) –15
B) –14
C) –13
■ f + g : A B→R
D) –12
E) –11
( f + g ) (x) = f(x) + g(x)
■ f – g : AB → R
( f – g ) (x) = f(x) – g(x)
■ f . g : A B→R
–––––––––––––––––––––––––––––––––––––––––––––––
26. Örnek:
( f . g ) (x) = f(x) . g(x)
f(x) – f(x+1) = x eşitliğinde f(2) = 20 olduğuna göre, f(6)
kaçtır?
■
A) 6
f
f(x)
, g(x) 0
(x)
g(x)
g
B) 5
C) 4
D) 3
E) 2
f
: A B R
g
29. Örnek:
f ve g birebir ve örten fonksiyondur.
27. Örnek:
f = {(–2, 4), (1, 4), (3, –2)}
Bir f fonksiyonu x N için, f(x + 1) = f(x) + 4 eşitliğini
sağlamaktadır.
g = {(–2, 3), (2, 1), (3, 2)} ise,
f(0) = 3 ise f(25) değeri kaçtır?
A) 132
B) 126
C) 112
2f + g aşağıdakilerden hangisidir?
D) 103
E) 100
A) {(–2, –2), (3, 11)}
B) {(–2,11), (3, –2)}
C) {(1, –2), (3, 11)}
D) {(–2, 5), (1, 12)}
E) {(3, –2), (–2, 11)}
www.idealmatematik.com
5
www.idealmatematik.com
Fonksiyonlar
30. Örnek:
34. Örnek:
R → R ye f ve g fonksiyonları
f(x) = 4x + 1
2
olduğuna göre, f(3x) in f(x) cinsinden değeri nedir?
f(x) = 2x – 3x ve g(x) = 5 + 2x olarak tanımlanmıştır.
(3f – g) (2) ifadesi aşağıdakilerden hangisine eşittir?
A) –3
B) –4
C) –5
D) –6
E) –7
A) 2f(x) – 1
B) 3f(x) – 2
D) 3f(x) + 2
E) 2f(x) + 1
C) 2f(x) + 1
31. Örnek:
35. Örnek:
f : N→ N
g : {(2,–1), (–1, 3), (5, 3)}
2x – 3
f(x) = 3
fonksiyonu için,
f(2x) in f(x) cinsinden eşiti aşağıdakilerden hangisidir?
2
f(x) = x – 2 fonksiyonları tanımlanıyor.
(4f + 3g) (–1) ifadesinin değeri kaçtır?
2
A) 9f (x)
A) –3
B) –1
C) 1
D) 3
B)
f(x)
27
E)
3f 2 (x)
4
E) 5
2
D) 27f (x)
C)
f 2 (x)
27
32. Örnek:
36. Örnek:
3x 5 , x asal sayı ise
f(x)
2x 2 , x>2 ve çift sayı ise
f(x)
5x 2
olduğuna göre,
3
3x 3
, x 4 ise
g(x) 2
3 x , x<4 ise
f(x – 3) fonksiyonunun f(x) cinsinden eşiti aşağıda–
kilerden hangisidir?
olduğuna göre, (f.g + 2.f) (5) kaçtır?
A) 3f(x) – 5
A) 60
B) 70
C) 80
D) 90
D) f(x) – 3
E) 100
3f(x) 19
3
E) 3f(x) – 15
B)
C) f(x) – 5
37. Örnek:
33. Örnek:
f(x)
2
2
f : R → R, f(x, y) = max (x + 1, xy + 2)
x
x3
2
g : R → R, g(x, y) = min (x + y, x – y)
olduğuna göre, f(x+3) ün f(x) türünden eşiti aşağıdakilerden
olduğuna göre, f(–3, 2) + 2g(–2, 2) toplamının eşiti
aşağıdakilerden hangisidir?
hangisidir?
A) 2
A)
3f(x) 1
f(x)
B)
f(x)
3f(x) 1
D)
f(x)
2f(x) 1
E)
2f(x) 1
f(x)
B) 3
C) 4
D) 5
E) 6
–––––––––––––––––––––––––––––––––––––––––––––––
www.idealmatematik.com
6
C)
f(x) 1
3f(x)
Fonksiyon Çeşitleri
www.idealmatematik.com
■ Bire – Bir Fonksiyon:
4. Örnek:
f : A→B fonksiyonu için, A kümesindeki farklı elemanların
görüntüleri de farklı ise, f(x) fonksiyonuna bire – bir
fonksiyon denir.
A = {1, 2, 3, 4, 5, 6} olmak üzere, f : A → A fonksiyonu
bire – birdir.
Buna göre,
Yani, x1 x 2 için f(x1 ) f(x 2 ) ise, y = f(x) fonksiyonu
bire – bir (1 : 1) fonksiyondur.
f(1) + f(2) + f(3) + f(4)
1. Örnek:
toplamının alabileceği en büyük değer ile en küçük
değer arasındaki fark kaçtır?
Aşağıdaki fonksiyonlardan hangisi bire – bir fonksiyondur?
A) f(x) = |x + 1|
A) 6
B) 7
C) 8
D) 9
2
B) f(x) = 6
E) 10
2013 – YGS
C) f(x) = x
6
D) f(x) = 5x
E) f(x) = x
■ Örten Fonksiyon ve İçine Fonksiyon:
f : A→B fonksiyonu için f(A) = B ise yani değer kümesi
görüntü kümesine eşit ise f fonksiyonuna örten fonksiyon
denir. Diğer bir deyişle değer kümesinde açıkta eleman
kalmıyor ise, fonksiyon örtendir.
2. Örnek:
Gerçel sayılar kümesinde tanımlı
I.
f : A→B fonksiyonu için f(A) ≠ B ise yani B kümesinde en
az bir eleman açıkta kalıyor ise, f fonksiyonuna içine
fonksiyon denir.
f(x) = 2x –1
2
II. g(x) = x + 2
III. h(x) = x
5. Örnek:
fonksiyonlarından hangileri bire birdir?
A = {a, b, c, d}
3
A) I ve II
B) Yalnız I
D) I ve III
E) Yalnız II
kümesi üzerinde tanımlı aşağıdaki fonksiyonların hangisi bire – bir ve örtendir?
C) I, II ve III
A) {(a, b), (b, a), (c, b), (d, c)}
(2011 – YGS)
B) {(a, a), (b, b), (c, d), (d, d)}
C) {(a, c), (b, d), (c, a), (d, b)}
D) {(a, b), (b, c), (c, d)}
E) {(a, b), (b, c), (c, c), (d, c)}
3. Örnek:
6. Örnek:
f(x) = 3x – 2 bire – bir ve örten fonksiyon olmak üzere,
f : A → B ve B = {–5, 1, 7} olduğuna göre,
f : A → B tanımlı
A kümesinin elemanları toplamı kaçtır?
f(x3) = y2
A) –1
koşulunu sağlayan kaç tane 1 : 1 fonksiyon vardır?
A) 16
B) 24
C) 36
www.idealmatematik.com
D) 48
E) 64
7
B) 0
C) 2
D) 3
E) 4
Fonksiyon Çeşitleri
www.idealmatematik.com
7. Örnek:
9. Örnek:
Z tamsayılar kümesi olmak üzere, f : Z → Z fonksiyonu
f: R → R olmak üzere,
x 1, x 0 ise
f(x)
x 1, x 0 ise
f(x) = (a – 2)x + (a – b)x + b + c
3
fonksiyonu birim fonksiyon olduğuna göre, a + b – c
ifadesinin eşiti kaçtır?
biçiminde tanımlanıyor.
A) 2
Buna göre,
I. f bire birdir.
II. f örtendir.
III. f’nin görüntü kümesi Z \ {0}’ dır.
B) 3
C) 4
D) 5
E) 6
10. Örnek:
f fonksiyonu birim fonksiyon olmak üzere,
ifadelerinden hangileri doğrudur?
2
f(x) = (a + 3)x + (2a + b)x + a – b + c olduğuna göre,
A) Yalnız I
B) Yalnız II
D) I ve II
E) I ve III
C) Yalnız III
f(a – b – c) kaçtır?
A) 20
(2012 – LYS)
B) 10
C) 0
D) –10
E) –20
8. Örnek:
11. Örnek:
Gerçel sayılardan gerçel sayıların bir K alt kümesine
tanımlı
f birim fonksiyonu
x 8, x 3 ise
f(x)
x 2, x 3 ise
f(3x) = 9ax + b – 12
biçiminde tanımlandığına göre, a . b çarpımı kaçtır?
fonksiyonu örten olduğuna göre, K kümesi
aşağıdakilerden hangisidir?
A) [3 , )
B) [5 , )
D) ( , 5)
E) ( , 3)
A) 36
C) [3 , 5]
B) 12
C) 6
D) 4
E) 3
■ Sabit Fonksiyon:
A kümesindeki tüm elemanları B deki yalnız bir elemanla
eşleyen fonksiyona sabit fonksiyon denir.
(2010 – LYS1 – Mat)
Her x A için f(x) = c ve c B ise f, A dan B ye tanımlı sabit
fonksiyondur.
12. Örnek:
■ Birim (Özdeş) Fonksiyon:
f sabit fonksiyon ve
f : A → A bir fonksiyon olsun.
Her x A için f(x) = x ise yani A daki her elemanı kendisine
eşleyen f fonksiyonuna birim (özdeş) fonksiyon denir.
olduğuna göre, f(2015) kaçtır?
x şeklinde yazılır.
Birim fonksiyonlar (x)
Birim fonksiyonlar bire – bir ve örtendir.
www.idealmatematik.com
2
f(x) = (4 –2a)x + (3a – b)x + 5a – b
A) 16
8
B) 4
C) 3
D) 2
E) 1
Fonksiyon Çeşitleri
www.idealmatematik.com
13. Örnek:
■ Doğrusal Fonksiyon:
f(x) = –2kx – 6x + 11
a, b R ve a ≠ 0 olmak üzere, f(x) = ax + b şeklinde ki
fonksiyonlara doğrusal fonksiyon denir.
bağıntısı sabit fonksiyon olduğuna göre, k kaçtır?
A) –3
B) –2
17. Örnek:
C) 0
D) 2
E) 3
f doğrusal fonksiyon ve
f(2) = 8
Not:
f(3) = 4
1) f(x)
ax b
a b
sabit fonksiyon ise, f(x) dir.
cx d
c d
olduğuna göre, f(5) kaçtır?
2) f : A → B tanımlanabilecek sabit fonksiyon sayısı, değer
kümesinin eleman sayısı kadardır. Yani, s(B) tane A dan B
ye sabit fonksiyon tanımlanabilir.
A) –4
B) 0
C) 4
D) 8
E) 12
D) 8
E) 9
D) –6
E) –4
14. Örnek:
18. Örnek:
2
f : R – { } → R olmak üzere,
3
f(x)
f doğrusal fonksiyon ve
9x m
3x 2
f(4) = 3
sabit fonksiyon olduğuna göre, m kaçtır?
f(6) = 11 ise,
A) –6
f(5) kaçtır?
B) –3
C) 0
D) 3
E) 6
A) 3
B) 5
C) 7
15. Örnek:
19. Örnek:
15x 9
f(x)
5x a
f doğrusal fonksiyon ve
fonksiyonu sabit fonksiyon olduğuna göre, f(2015) değeri
kaçtır?
f(x – 1) + f(x + 2) = 6x – 1
A) –3
A) –12
B) –1
C) 0
D) 3
olduğuna göre, f(–2) kaçtır?
E) 5
16. Örnek:
f(x – 3) + f(x) = –10x + 21
3x m 2
5x 10
olduğuna göre, f(–1) + f(1) toplamı kaçtır?
A) –6
fonksiyonunun sabit fonksiyon olması için m kaç
olmalıdır?
A) 4
B) 2
C) –8
20. Örnek:
5x ≠ 10 olmak üzere,
f(x)
B) –10
C) 1
www.idealmatematik.com
D) –1
E) –4
9
B) –5
C) 5
D) 6
E) 7
www.idealmatematik.com
Ters Fonksiyon
■ Ters Fonksiyon:
3. Örnek:
f : A → B fonksiyonu bire – bir ve örten ise, f fonksiyonunun
–1
tersi vardır ve f : B → A şeklinde gösterilir.
f bire – bir ve örten bir fonksiyondur.
5x 1
f
x
3 2x
–1
f(x) = y ise f (y) = x
–1
olduğuna göre, f (x) ters fonksiyonu aşağıdakilerden
hangisidir?
f
A
B
2x 1
3 5x
1 5x
E)
2x 3
2x 1
3 5x
5x 1
D)
2x 3
A)
B)
C)
x2
5 3x
f1
f (A) = B
–1
A = f (B)
4. Örnek:
f bire – bir ve örten fonksiyondur.
f(5) = 4
1. Örnek:
–1
f (3) = –2 ise,
{1, 2, 3} kümesinden {10, 11, 12} kümesine aşağıdaki
fonksiyonlar tanımlanıyor.
–1
f (4) + f(–2) kaçtır?
Bu fonksiyonlardan hangisinin ters fonksiyonu vardır?
A) 2
B) 4
C) 6
D) 8
E) 10
A) {(1, 11), (2, 10), (3, 12)}
B) {(1, 12), (2, 11), (3, 11)}
C) {(1, 10), (2, 10), (3, 11)}
D) {(1, 10), (2, 10), {3, 10)}
5. Örnek:
E) {(1, 12), (2, 11), (3, 12)}
(1988 – ÖYS)
f(4x + 3) = 5x – 2 olduğuna göre,
–1
f(–5) + f (8) ifadesinin değeri kaçtır?
A) –5
B) –1
C) 3
D) 5
E) 13
D) 1
E) 2
2. Örnek:
f = {(–3, 5), (0, 4), (–1, 3), (4, –3)}
–1
6. Örnek:
–1
olduğuna göre, f(–3) – f (3) + f (–3) ifadesinin değeri
kaçtır?
f(x –2
A) 8
olduğuna göre, f (28) kaçtır?
B) 9
C) 10
D) 11
3
x
) = 5 +3
–1
E) 12
A) –2
www.idealmatematik.com
x+1
10
B) –1
C) 0
www.idealmatematik.com
Ters Fonksiyon
7. Örnek:
Bir Fonksiyonun Ters Fonksiyonunun Bulunuşu:
f(x) = ax + b
■ f : A → B ye bire – bir ve örten fonksiyon olsun.
f (2) = 5
y = f(x) fonksiyonunda x yalnız bırakıldıktan sonra x ile y
–1
nin yerleri değiştirilerek f fonksiyonunun tersi olan f
fonksiyonu bulunur.
olduğuna göre, a.b çarpımı kaçtır?
11. Örnek:
–1
f (3) = 4
–1
A) –7
B) –6
C) –5
D) 3
E) 6
f : R – {–1} → R – {3}
(1996 – ÖYS)
x
f(x) 2
3 f(x)
–1
olduğuna göre, f (x) aşağıdakilerden hangisidir?
8. Örnek:
–1
2
B) 4
C) 5
x 3
x 1
B)
x3
x2
D)
2x 1
3x
E)
2x 3
3x
–1
f(x + 2x – 4) = (x – 2) . f (x) + 5 olduğuna göre, f (5)
kaçtır?
A) 3
A)
D) 6
C)
x2
3x
(1997 – ÖSS)
E) 7
12. Örnek:
f : R – {0} → R – {–
2
} tanımlı y = f(x) fonksiyonu
5
2x + 5xy – 3 = 0
9. Örnek:
–1
olduğuna göre, f (x) fonksiyonunu bulunuz.
f(3x + 2) = 5x – m
–1
f (18) = 11 olduğuna göre, m kaçtır?
A) –3
B) –2
C) –1
D) 1
E) 3
A)
5x 2
3
B)
5x 3
2
D)
3
2 5x
E)
3
2 5x
C)
2
3 5x
13. Örnek:
10. Örnek:
R de tanımlı,
f : (– , 2) → (–5 , )
f(x) = 3x – 4
2
f(x) = x – 4x – 9
–1
olduğuna göre, f (x) aşağıdakilerden hangisine eşittir?
–1
olduğuna göre, f (3) kaçtır?
A) –6
B) –2
C) 0
www.idealmatematik.com
D) 2
E) 6
11
A)
x 3
4
B)
3
x4
D)
x4
3
E)
x4
3
C) 3x + 4
www.idealmatematik.com
Ters Fonksiyon
14. Örnek:
18. Örnek:
f : R → R olmak üzere,
1
, ) R , f(x) log3 (3x 1) ile tanımlanıyor.
3
–1
Buna göre, ters fonksiyonu belirten f (x) aşağıdakilerden
hangisidir?
f :(
f(x) 5 x 2
–1
olduğuna göre, f (x) fonksiyonu aşağıdakilerden hangisidir?
A)
5
x2
B)
x5 2
5
E)
x5 2
D) x – 2
–1
A) f (x) = 3
x
B) f (x) = 3 +1
3x 1
3
–1
D) f (x) =
5
C) x + 2
–1
x
–1
E) f (x) =
–1
C) f (x) = log(3x+1)
x3 1
3
(2006 – ÖSS – 2)
15. Örnek:
Kural:
f : (–3, ) → (–5, ) olmak üzere,
■ a≠0 olmak üzere, f(x) = ax + b ise f 1(x)
f(x) x 3 5
2
A) x + 5
2
C) (x + 5) – 3
B) x + 5
2
2
D) (x + 3) – 5
ax b
dx b
ise f 1(x)
cx d
cx a
■ f(x)
–1
olduğuna göre, f (x) aşağıdakilerden hangisine eşittir?
x b
a
E) (x – 3) + 5
19. Örnek:
R de tanımlı,
f(x) = 5x – 3
–1
16. Örnek:
olduğuna göre, f (x) aşağıdakilerden hangisine eşittir?
f : ( 0 , ) → ( –3 , ) olmak üzere,
A)
x3
5
B)
5
x3
D)
x 3
5
E)
x5
3
2
f(x) = x – 3
–1
olduğuna göre, f (x) aşağıdakilerden hangisine eşittir?
A)
x 3
B)
x3
D)
x 3
E)
x 3
C)
C) 5x + 3
x 3
20. Örnek:
f:R–{
17. Örnek:
f(x)
f : ( 4 , ) → ( –5 , )
5
3
}→ R – { }
4
4
3x 2
4x 5
2
f (x) = x – 8x + 11
–1
olduğuna göre, f (1) kaçtır?
–1
olduğuna göre, f (x – 5) aşağıdakilerden hangisidir?
A)
x 4
D) 2 x 1
B)
x 4
E)
x5 4
www.idealmatematik.com
A) –5
C) 2 x 1
12
B) –3
C) 0
D) 5
E) 7
www.idealmatematik.com
Ters Fonksiyon
21. Örnek:
f(x)
25. Örnek:
5x 9
6x a
3x 2, x 4
f(x)
x 3, x 4
–1
fonksiyonu için f(x) = f (x) olduğuna göre, f(2) kaçtır?
A) 8
B) 7
C) 1
D)
1
7
E)
–1
olduğuna göre, f (10) kaçtır?
1
9
A) 8
B) 7
C) 6
D) 5
E) 4
––––––––––––––––––––––––––––––––––––––––––––––
22. Örnek:
26. Örnek:
R – {1} de tanımlanan
f(2x + 3) = 8x – 4 olduğuna göre,
2x 1
f(x)
x 1
f(x) aşağıdakilerden hangisine eşittir?
fonksiyonunun değer kümesi aşağıdakilerden
hangisidir?
A) 4x
B) 4x + 2
D) 4x + 16
E) 8x + 16
A) R
B) R – {3}
D) R – {1}
E) R – {0}
C) 4x – 16
C) R – {2}
(1998 – ÖSS)
27. Örnek:
2x 1
f
x 2 ise,
3x 1
23. Örnek:
f : R – {2} → R – {3}
f(x) aşağıdakilerden hangisine eşittir?
ax 4
f(x)
3x b
A)
veriliyor.
5x 5
3x 2
D) 3x – 2
f(x) fonksiyonu bire–bir ve örten olduğuna göre, (a, b) sıralı
ikilisi aşağıdakilerden hangisidir?
A) (5 , 4)
B) (2 , 3)
D) (6 , 6)
E) (9 , 6)
B)
3x 2
5x 5
E)
5 5x
3x 2
C) –5x + 5
C) (2 , 6)
(1997 – ÖYS)
28. Örnek:
24. Örnek:
5
x3
f
1 olduğuna göre,
x2 x3
f : R – {a + 2} → R – {b – 2} olmak koşuluyla,
f(x)
f(x) fonksiyonu aşağıdakilerden hangisidir?
4x 7
fonksiyonunun tersinin olduğu bilindiğine
2x 6
A)
göre, a . b çarpımı kaçtır?
A) –20
B) –10
C) –5
www.idealmatematik.com
D) 4
E) 20
13
x
3
B)
1
x
C)
1
x
D) –x
E)
2
x
Bileşke Fonksiyon
www.idealmatematik.com
■ Bileşke Fonksiyon:
3. Örnek:
f : A → B ve g : B → C olmak üzere,
f(x) = 3x – 6
2
g(x) = (x – 2)
gof : A → C fonksiyonuna g ile f fonksiyonlarının bileşke
fonksiyonu denir.
f
x
–1
Buna göre, (gof )(x) aşağıdakilerden hangisine eşittir?
C
B
A
fonksiyonları veriliyor.
3x 2
1
2
x2
D)
9
A)
g
y
z
B) (3x + 4)
E) (3x – 8)
2
2
C) x – 4x + 2
2
(2011 – YGS)
–––––––––––––––––––––––––––––––––––––––––––––––
4. Örnek:
gof
f ve g gerçek sayılarda tanımlı fonksiyonlardır.
(gof)(x) = g(f(x))
2
g(x) = 3x +1
5
f(x) = x – 1
olduğuna göre, (gof)(–1) ifadesinin değeri kaçtır?
1. Örnek:
A) 13
f ve g gerçek sayılarda tanımlı fonksiyonlardır.
B) 14
C) 15
D) 16
E) 17
g(x) = 3x+4
f(x) = 2x–1
5. Örnek:
olduğuna göre, (fog)(x) fonksiyonu aşağıdakilerden
hangisidir?
A) 6x–1
B) 6x+1
D) 6x–7
E) 5x+3
f ve g gerçek sayılarda tanımlı fonksiyonlardır.
g(3x+1) = 5x–1
2
f(x+3) = 2x
C) 6x+7
olduğuna göre, (fog)(7) ifadesinin değeri kaçtır?
A) 25
B) 36
C) 50
D) 72
E) 162
2. Örnek:
6. Örnek:
f ve g gerçek sayılarda tanımlı fonksiyonlardır.
Tam sayılar kümesinden tam sayılar kümesine f ve g
fonksiyonları aşağıdaki biçimde tanımlanmıştır.
f(x) = x – 3
g(x) = 3x – 5
2x 1 , x 0(mod 2) ise
f(x)
x 1(mod 2) ise
3x ,
olduğuna göre, (gof)(x) fonksiyonu aşağıdakilerden
hangisidir?
A) 3x–8
B) 3x+8
D) 3x+4
E) 3x–14
x 0(mod 3) ise
x ,
g(x) 3x 1 , x 1(mod 3) ise
x 1 , x 2(mod 3) ise
C) 3x+14
Buna göre, g(f(6)) değeri kaçtır?
A) 55
B) 40
C) 18
D) 17
E) 12
(2009 – ÖSS)
www.idealmatematik.com
14
Bileşke Fonksiyon
www.idealmatematik.com
7. Örnek:
11. Örnek:
f : R → R parçalı fonksiyonu
f(x) = x + 2x
2
2
(fog)(x) = x + 6x + 8
3x 1 , x rasyonelse
f(x) 2
x rasyonel değilse
x ,
olduğuna göre, g(x) aşağıdakilerden hangisi olabilir?
2
biçiminde tanımlanıyor.
2
Buna göre, (fof)
aşağıdakilerden hangisidir?
2
A) 3 2 2
D)
5
2
2 2
B)
E)
C)
2
A) x + x
B) x – 2
D) x – 2
E) x + 2
2
C) x + 2
(1994 – ÖSS)
1
4
12. Örnek:
7
2
(fof)(x) = 16x + 15 olduğuna göre,
f(x) fonksiyonu aşağıdakilerden hangisi olabilir?
(2011 – LYS)
8. Örnek:
A) 4x + 5
B) 4x – 3
D) –4x + 5
E) 4x – 5
C) –4x – 5
f(x) = 4x + 3 ve
g(x) = 2x – 3 fonksiyonları veriliyor.
13. Örnek:
(fog)(x) = 31 olduğuna göre, x kaçtır?
A) 7
B) 5
C) 3
D) 1
E) –1
g(3x – 2) = 6x – 3
–1
(g o f)(x) = x – 6 olduğuna göre,
f(x) fonksiyonu aşağıdakilerden hangisidir?
9. Örnek:
f(x) = 2x + 1,
A) 2x + 11
B) 2x – 7
D) 2x – 11
E) x – 7
C) 2x + 7
2x 1
g(x)
,
x5
–1
(g of)(x) = –16
14. Örnek:
olduğuna göre, x kaçtır?
f(x)
A) 1
B) 2
C) 3
D) 4
E) 8
2x u
x 9
ve (fof )(x)
x 1
3x 2
olduğuna göre u kaçtır?
(1995 – ÖYS)
A) –3
B) –2
C) –1
D) 0
–––––––––––––––––––––––––––––––––––––––––––––––
10. Örnek:
(fog)(x)
(1990 – ÖYS)
x
ve g(x) = x + 1
x2 1
–––––––––––––––––––––––––––––––––––––––––––––––
15. Örnek:
olduğuna göre, f(x) fonksiyonu aşağıdakilerden hangisidir?
A)
x 1
x 2x 2
B)
x 1
x 2x 2
D)
x2 1
x
E)
x
x 1
2
2
C)
f(x) = 5x + 2 ve
(gof)(x) = 8x – 6 olduğuna göre,
x2 1
x 1
g(7) kaçtır?
A) 0
(1988 – ÖYS)
www.idealmatematik.com
E) 1
15
B) 1
C) 2
D) 3
E) 4
Bileşke Fonksiyon
www.idealmatematik.com
16. Örnek:
21. Örnek:
(fog)(x) = 4x + 2 ve
Uygun şartlarda tanımlı f(x) ve g(x) fonksiyonları için,
g(x) = 2x – 1 olduğuna göre,
–1
f (x) = 4x – 3 ve
–1
(f og)(x) = 2x + 1 olduğuna göre,
–1
f (–6) kaçtır?
A) –5
B) –4
C) 0
D) 4
–1
g (4) kaçtır?
E) 5
A) 4
B) 5
C) 6
D) 7
E) 8
D) 94
E) 96
17. Örnek:
f(x) = x – 1 ve (gof)(x) = x – 2x + 3 olduğuna göre,
22. Örnek:
(fog)(3) kaçtır?
f(2x–1) = 3x – 2
3
A) 26
B) 32
C) 44
D) 55
–1
2
(f og)(x) = x .f(x+2)
E) 58
olduğuna göre, g(3) kaçtır?
A) 88
B) 90
C) 92
–––––––––––––––––––––––––––––––––––––––––––––––
18. Örnek:
(fog)(x) = 4.g(x) – 5
(gof)(x) = 3.f(x) + 2 olduğuna göre,
23. Örnek:
(gof)(2) kaçtır?
f ve g, birebir ve örten fonksiyonlardır.
A) 9
B) 11
C) 16
D) 19
–1
–1
(f og)(x) = 7x + 2 ve g (9) = 1
E) 27
olduğuna göre, f(9) kaçtır?
A) 10
B) 9
C) 8
D) 7
E) 6
19. Örnek:
f ve g fonksiyonları için,
NOT:
2
(fog)(x) = 2g (x) – 3g(x) + 1
(gof)(x) = 2f(x) + 3 olduğuna göre,
–1
■ fof
(fog)(–1) kaçtır?
A) 15
B) 10
–1
= f of =
■ f o = o f = f
C) 5
D) 0
■ (fog)
E) –5
–1
–1
–1
= g of
–1
–1
–1
■ (fogoh) = h o g o f
–1 –1
■ (f )
–1
=f
–––––––––––––––––––––––––––––––––––––––––––––––
20. Örnek:
24. Örnek:
g birebir ve örten fonksiyondur.
f ve g R den R ye tanımlı fonksiyonlar olmak üzere,
f(5x – 2) = g(4x + 1) eşitliğine göre,
–1
g(x) = 4x + 1 ve (fog) (x) = 2x – 4
–1
(g of)(8) kaçtır?
–1
olduğuna göre, f (5) kaçtır?
A) 9
B) 8
C) 7
D) 6
E) 5
A) 25
www.idealmatematik.com
16
B) 22
C) 19
D) 16
E) 8
Bileşke Fonksiyon ve Fonksiyon Grafikleri
www.idealmatematik.com
25. Örnek:
29. Örnek:
f(3x + 2) = 5x – 2
Bir y = f(x) fonksiyonunun
g(x – 3) = 2x – 2
grafiği yanda verilmiştir.
–1
f[f(x)] = 3 olduğuna göre,
–1
olduğuna göre, (g of) (2) ifadesinin sonucu kaçtır?
A) 4
B) 5
C) 6
D) 7
x in değeri nedir?
E) 8
A) 7
B) 6
C) 5
D) 4
E) 3
(1982 – ÖYS)
26. Örnek:
30. Örnek:
f(x) = 3x + 1
–1
g (x) = x – 2
–1
y
y=f(x)
–1
7
(f og) (m) = 8 olduğuna göre, m kaçtır?
A) 0
B) 1
C) 2
D) 3
E) 4
5
4
5
-3
-5
x
-4
27. Örnek:
–1
Yukarıda y : R → R, y = f(x) fonksiyonunun grafiği
verilmiştir.
f (4x – 1) = g(2x + 1)
–1
olduğuna göre, (fog) (11) ifadesinin değeri kaçtır?
A) 9
B) 8
C) 7
D) 6
–1
Buna göre, f (7) + (fof)(–3) + f(0) toplamının sonucu
kaçtır?
E) 5
A) –5
–––––––––––––––––––––––––––––––––––––––––––––––
28. Örnek:
B) –3
C) 2
D) 4
E) 6
31. Örnek:
y=f(x)
Aşağıda f fonksiyonunun grafiği verilmiştir.
y
4
2
4
x
-3
g(x) = 3 – f(x – 2) olduğuna göre,
Yukarıdaki y = f(x) in grafiğine göre,
g(–2) + g(5) toplamı kaçtır?
A) –3
B) –1
C) 1
D) 2
f[f[f(3n – 12)]] = 2 şartını sağlayan n kaçtır?
E) 3
A) –3
(2011 – LYS)
www.idealmatematik.com
17
B) –1
C) 0
D) 1
E) 3
Bileşke Fonksiyon ve Fonksiyon Grafikleri
32. Örnek:
35. Örnek:
Yanda grafiği verilen
f(x) fonksiyonu [0, 2] de
bire bir ve örtendir.
6
f(2) f 1(2)
f(f(1))
ifadesinin değeri kaçtır?
3
4
0
-4
3
B)
2
y
y=f(x)
Buna göre,
5
A)
2
www.idealmatematik.com
C) 0
1
D)
2
3
E)
2
x
2
-4
(1997 – ÖYS)
y = f(x) fonksiyonunun grafiği şekilde verilmiştir.
–1
f(x – 1) = f (6) olduğuna göre, x kaçtır?
33. Örnek:
A) –4
B) –2
C) 0
D) 3
E) 5
–––––––––––––––––––––––––––––––––––––––––––––––
36. Örnek:
y
4
2
Yukarıda f(x) ve g(x) fonksiyonlarının grafiği verilmiştir.
4
Grafikteki bilgilere göre,
A)
1
2
B) –1
g(1) (fog)(2)
değeri kaçtır?
f(4)
C) 0
D) 1
x
-1
y=f(x-2)
1
2
E)
5
-3
Şekilde f(x – 2) fonksiyonunun grafiği verilmiştir.
f(3) f 1(4)
ifadesinin değeri kaçtır?
f(2) f 1(2)
(1998 – ÖSS)
A) 3
34. Örnek:
B) 2
D)
C) –2
5
2
E) –3
37. Örnek:
y
f(x-1)
-3
Yukarıdaki şekilde, f(x) fonksiyonu ile g(x) = x
fonksiyonunun grafikleri verilmiştir.
C) 0
www.idealmatematik.com
D) 4
5
x
Şekilde f(x–1) fonksiyonunun grafiği verilmiştir.
–1
B) –2
2
3
Buna göre (fog of)(0) değeri kaçtır?
A) –4
0
Buna göre, f(x + 1) = 0 denklemini sağlayan farklı x
değerlerinin toplamı kaçtır?
E) 8
(2000 – ÖSS)
A) –2
18
B) –1
C) 0
D) 1
E) 2
Bileşke Fonksiyon ve Fonksiyon Grafikleri
38. Örnek:
www.idealmatematik.com
41. Örnek:
y
6
2
1
4
3
0
-2
x
f 1(x 2)
Şekilde f ve g fonksiyonlarının grafikleri verilmiştir.
–1
f (x + 2) fonksiyonunun grafiği verilmiştir.
Buna göre, (gog)(2) + (gof
–1
)(0) toplamı kaçtır?
1
Buna göre,
A) –6
B)
f(1) f (0)
ifadesinin sonucu kaçtır?
f 1(2) f(6)
1
8
C)
11
2
D) 3
A) 6
B) 8
C) 10
D) 12
E) 14
E) 11
42. Örnek:
39. Örnek:
y
2
5
1
3
-4
x
-2
y=(gof)(x)
Yandaki grafik f(x) fonksiyonuna aittir.
Yukarıda (gof)(x) fonksiyonunun grafiği verilmiştir.
–1 –1
Buna göre, (fog )
kaçtır?
–1
f(3) = 5 olduğuna göre, g (2) kaçtır?
A) –5
B) –3
C) 1
D) 3
A) 9
E) 5
40. Örnek:
B) 8
2
(x) = 2x – 9x + 3 olduğuna göre, g(0)
C) 7
D) 6
E) 5
43. Örnek:
Yukarıdaki grafik f(x) fonksiyonuna aittir.
(fog)(x) ve f(x) fonksiyonlarının grafiği verilmiştir.
f(x 1) f(x 3)
eşitliği ve
f(2x 1)
g(3) = 1 olduğuna göre, f(2) kaçtır?
g(x)
Buna göre, g(4) kaçtır?
A) –14
B) –13
C) –12
D) –10
E) –8
A) 12
www.idealmatematik.com
19
B) 9
C) 8
D) 5
E) 3
Permütasyon Fonksiyon
www.idealmatematik.com
Permütasyon Fonksiyon:
3. Örnek:
■ f : A → A tanımlı bire bir ve örten her fonksiyona A nın
bir permütasyonu denir.
A = {a, b, c, d, e} kümesi üzerinde tanımlı f ve gof
permütasyon fonksiyonları,
■ A dan A ya tanımlanan permütasyon fonksiyonların
sayısı n! dir.
a b
f
c e
a
gof
c
1. Örnek:
olduğuna göre, g fonksiyonunu bulunuz.
c d e
a b d
b c d e
d e a b
A = {1, 2, 3, 4, 5, 6} kümesi üzerinde tanımlı f permütasyon
fonksiyonu
1 2 3 4 5 6
f
3 4 5 6 1 2
–1
f =
4. Örnek:
a) f(3) =
–1
b) f(5) =
A = {1, 2, 3, 4, 5, 6} kümesi üzerinde tanımlı f ve g
permütasyon fonksiyonları
–1
c) f (6) =
d) f (4) =
e) (fof)(1) =
f) (fof)(3f(6)) =
1 2 3 4 5 6
f
2 3 1 5 6 4
g)(fofof)(x) = 4 olduğuna göre, x =
1 2 3 4 5 6
g
6 5 4 1 2 3
olduğuna göre, (f – 2g)(4) + (g – f)(2) ifadesinin değeri
kaçtır?
2. Örnek:
A) 1
B) 2
C) 3
D) 4
E) 5
A = {1, 2, 3, 4, 5, 6} kümesi üzerinde tanımlı f ve g
permütasyon fonksiyonları
5. Örnek:
1 2 3 4 5 6
f
2 3 1 5 6 4
A = {1, 2, 3, 4, 5, 6} kümesi üzerinde,
1 2 3 4 5 6
f
2 3 1 5 6 4
1 2 3 4 5 6
g
olduğuna göre,
6 5 4 1 2 3
fonksiyonları tanımlandığına göre, (fofof)(4) kaçtır?
a) fog bileşke fonksiyonunu bulunuz.
A) 1
B) 2
C) 3
D) 4
E) 5
6. Örnek:
A = {a, b, c, d, e} kümesi üzerinde,
a b
f
c d
a b
g
b c
b) gof bileşke fonksiyonunu bulunuz.
c d e
e a b
c d e
a e d
olduğuna göre, (fog)(d) ifadesinin eşiti aşağıdakilerden
hangisidir?
A) a
www.idealmatematik.com
20
B) b
C) c
D) d
E) e
Permütasyon Fonksiyon
7. Örnek:
A = {1, 2, 3, 4, 5} kümesi üzerinde tanımlanan
1 2 3 4 5
f
3 1 5 2 4
1 2 3 4 5
g
5 3 4 1 2
–1
permütasyonları için g(f (2)) değeri kaçtır?
A) 1
B) 2
C) 3
D) 4
E) 5
(2010 – LYS)
8. Örnek:
A = {1,2, 3, 4, 5} kümesi üzerinde,
1 2 3 4 5
f
2 3 1 5 4
,
1 2 3 4 5
g
5 1 4 2 3
–1
(fog )(x) = 5 olduğuna göre, x kaçtır?
A) 1
B) 2
C) 3
D) 4
E) 5
9. Örnek:
A = {1, 2, 3, 4, 5} kümesinde,
1 2 3 4 5
f
2 3 1 5 4
,
1 2 3 4 5
fog1
5 1 4 2 3
olduğuna göre, g(1) kaçtır?
A) 1
B) 2
C) 3
www.idealmatematik.com
D) 4
E) 5
21
www.idealmatematik.com









