Tek ve Çift Fonksiyonlar Bir Fonksiyonun En Geniş

Fonksiyonlar
Konu Özeti
y
y
f(x1)
3.
Köklü fonksiyonların en geniş tanım kümesi:

f(x)  2n g(x) fonksiyonun en geniş tanım kümesi,
g(x)  0 koşulunu sağlayan x noktalar kümesidir.
f(x2)
f(x1)
a

x1
x2
b
x
f(x2)
a x1
x2
b
f, (a, b) aralýðýnda
f, (a, b) aralýðýnda
artan fonksiyondur.
azalan fonksiyondur.
f(x)  2n1 g(x)
fonksiyonu g(x) in tanımlı olduğu
tüm reel sayılarda tanımlıdır.
x
4.
f(x) = logh(x) •g(x)œ biçimindeki logaritma fonksiyonlarının en geniş tanım kümesi:
h(x) > 0 , h(x)  1 ve g(x) > 0 koşullarını sağlayan ortak noktalar kümesidir.
Tek ve Çift Fonksiyonlar
Özel Tanýmlý Fonksiyonlar
Tanım: f: [–a, a]  R , y = f(x) fonksiyonu verilsin.
1.
Parçalý Fonksiyonlar
 x  [–a, a] için f(–x) = – f(x) oluyorsa, f fonksiyoTanım kümesinin alt aralıklarında farklı birer kuralla ta-
nuna tek fonksiyon denir.
nımlanan fonksiyonlara parçalı fonksiyonlar denir.
 x  [–a, a] için f(–x) = f(x) oluyorsa, f fonksiyo-
g(x) , x  a
f: R  R , f(x)  
h(x) , x  a

Polinom şeklindeki tek fonksiyonlarda çift dereceli terimlerin katsayıları sıfırdır.

Polinom şeklindeki çift fonksiyonlarda tek dereceli terimlerin katsayıları sıfırdır.
Bireysel Yetenek
nuna çiftk fonksiyon denir.
fonksiyonu parçalı fonksiyondur. Burada alt aralıkların
uç noktası olan x = a noktasına fonksiyonun kritik noktası denir.

Parçalı fonksiyonların grafikleri çizilirken, tanım aralığı-

Tek fonksiyonların grafikleri orjine göre simetriktir.
nın her alt aralığındaki farklı kuralla tanımlanmış fonk-

Çift fonksiyonların grafikleri y eksenine göre simet-
siyonların grafikleri ayrı ayrı çizilerek grafik belirlenir.
riktir.

2.
tek veya çift fonksiyon olmayabilir.
 f(x) , f(x)  0
| f(x) |  
  f(x) , f(x)  0
Bir Fonksiyonun En Geniþ Taným Kümesi
1.
biçiminde tanımlanan y = |f(x)| fonksiyonuna mutlak
Polinom fonksiyonların en geniş tanım kümesi:
xn – 1 + ... + a x + a biçimindeki
P(x) = a xn + a
değer fonksiyonu denir. Mutlak değerin içini sıfır ya-
polinom fonksiyonlar tüm reel sayılarda tanımlıdır.
siyonun kritik noktaları denir.
n
2.
Mutlak Deðer Fonksiyonu
Bir fonksiyon hem tek hem de çift olabileceği gibi,
n–1
1
pan yani f (x) = 0 şartını sağlayan x değerlerine fonk-
0

Rasyonel fonksiyonların en geniş tanım kümesi:
f(x)
f(x) ve g(x) polinom fonksiyon olmak üzere, h(x) 
g(x)
fonksiyonu g(x) = 0 şartını sağlayan x değerlerinde
Mutlak değer fonksiyonunun grafiği:
y = |f(x)| in grafiği çizilirken önce y = f(x) fonksiyonunun grafiği çizilir. Daha sonra x ekseninin altında kalan kısmın x eksenine göre simetriği alınır. Dolayı-
tanımsızdır. O halde en geniş tanım kümesi,
sıyla fonksiyon kritik noktalarında kırılma ya da kıv-
R – 7x: g(x) = 0? dır.
rılma yapar. Aşağıdaki şekilleri inceleyiniz.
6
Fonksiyonlar
Konu Özeti
y
2.
y
2
2
y=x –1
y = |x – 1|
1
–1
0
1
x
–1
0
x
1
f: R  R , f(x) = | ax – b | – | mx – n | , (m  a) fonksib
yonunun grafiği, mutlak değer içlerini sıfır yapan
a
n
ve
değerlerinde kırılma yapar. Bu değerlerden
m
küçük olanına x1 ve büyük olanına x2 diyelim. Grafik, aşağıdaki üç farklı durumlarda oluşabilir.
–1
–1
y
Mutlak değer içleri f(x) = ax + b biçiminde olan, iki
y
x1
mutlak değer toplamından oluşan fonksiyonların grafik-
0
x
x2
x1
0
x2
x
leri aşağıda verilen şekillerdeki gibi oluşur. İnceleyiniz.
1.
f: R  R,
y
Minimum ve maksimum
Maksimum deðeri vardýr.
deðer yoktur.
f(x) = | x – a| + | x – b| fonksiyonunun grafiği x = a ve x = b
y
|a – b|
de kırılma yapan ve minimum
değeri f(a) = f(b) = |a – b| olan
a
0
x
b
x1
0
2.
f: R  R,
Bireysel Yetenek
yandaki şekli çizer.
y
f(x) = | ax – b | + | mx – n |,
m  a grafiği, mutlak değer
n
b
içlerini sıfır yapan
ve
m
a
değerlerinde kırılma yapar.
f(x2)
f(x1)
0
Bu değerlerden küçük ola-
x1
x
Minimum deðeri vardýr.
O halde f(x) = | ax – b | – | mx – n | fonksiyonunun minimum veya maksimum değeri (varsa) kritik noktala-
x
x2
x2
rın birinde oluşur.
nına x1 ve büyük olanına x2 diyelim. Fonksiyonun
f(x1) ya da f(x2) de bir minimum değeri oluşur. Fonkf(x) = |ax – b| – |mx – n| biçimindeki fonksiyonların
siyonun grafiği yanda görüldüğü gibidir.
grafiklerini çizmek için, aşağıdaki aşamalar izlenmelidir.
Mutlak değer içleri f(x) = ax + b biçiminde olan, iki
mutlak değer farkından oluşan fonksiyonların grafikleri aşağıda verilen şekillerdeki gibi oluşur. İnceleyiniz.

Kritik noktalar ve görüntüleri bulunur.

Soldaki kritik noktanın solunda bir nokta seçilip bu
noktanın görüntüsü bulunur. Bu iki nokta birleştirilip
1.
f: R  R,
grafiğin sol kısmı çizilir.
y
f(x) = | x – a| – | x – b| fonk-
|a – b|
siyonunun grafiği x = a ve
a
x = b de kırılma yapar. Bu
0
b
x
İki kritik nokta birleştirilir.

Sağdaki kritik noktanın sağında bir nokta seçilip bu noktanın görüntüsü bulunur. Bu iki nokta birleştirilip grafiğin
noktaların birinde minimum
değer, diğerinde maksi-

sağ kısmı çizilir. Böylece grafik tamamlanmış olur.
–|a – b|
mum değer oluşur. Şekilde,
f(a) = –|a – b| (minimum değer)
f(b) = |b – a| = |a – b| (maksimum değer) dir.
7
Sentez – Deðerlendirme
Mutlak Deðer Fonksiyonu
1.
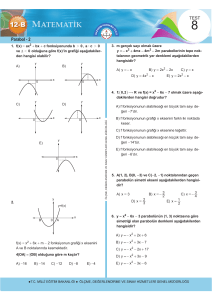
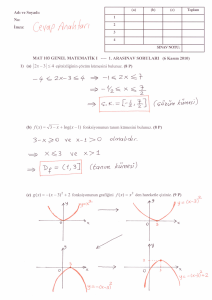
Test No: 12
Analitik düzlemde çözüm kümesi yandaki
denklemini sağlayan kaç farklı x reel sayısı vardır?
2
grafikte verilen eşitsizlik sistemi aşağıda-
2
kilerden hangisidir?
A) 0
x
0
–2
| 2–x – 2 | = | x2 – 9 |
3.
y
B) 1
C) 2
D) 3
E) 4
–2
4.
A) | x | + | y |  2
B) | x | – | y |  2
|x|  1
| x.y |  0
C) | x + y |  2
D) | x + y |  2
x .y  0
x .y  0
| x | + | –y | = 2x
bağıntısının grafiği koordinat düzleminde aşağıdakilerden hangisini belirtir?
A) Paralelkenar
B) Eşkenar dörtgen
E) | x + y |  2
C) Paralel iki doğru parçası
x.y  0
D) Birbirine dik iki ışın
E) Orjinde kesişen iki doğru
Yanda grafiği verilen
y
5.
f(x + 3) fonksiyonu
f(x + 3)
için,
y
f(x)  f 2(x)
2
–4
–1
0
x
2
Yanda grafiği verilen
y
f(x) fonksiyonunun eşi-
Bireysel Yetenek
2.
f(x)
ti aşağıdakilerden hangisi olabilir?
1
0
1
2
x
fonksiyonunun grafiği aşağıdakilerden hangisidir?
A)
B)
y
y
A) f(x) = - | x | – 2 -
B) f(x) = | x – 1 | – 1
C) f(x) = - 2 | x – 1 | – 1 -
D) f(x) = - | x – 1 | – 1 -
E) f(x) = | x – 2 | + | x + 1 |
–4
–1 0
2
x
–4
–1 0
2
x
6.
C)
D)
y
Yanda grafiği verilen
y
bağıntının eşiti aşa-
y
ğıdakilerden hangisi
olabilir? (e,  irrasyonel sayılardır.)
–1 0
2
5
x
–1 0
E)
2
5
0
x
x
y
–7
–4
–1 0
x
A) | x | – | y | = 2
B) | x .y | = e – 
C) | x |.| y | = 2
D) | x – 1|.| y | = | x |
E)
35
x
1
y
Sentez – Deðerlendirme
Mutlak Deðer Fonksiyonu
7.
Test No: 12
Yanda grafiği verilen
9.
y
f(x) fonksiyonu için
f(x)
2
y = f ‡|x| fonksiyonunun grafiği aşağıda-
y  f(x) 
x
2
0
B)
y
C)
x
2
–2
A)
0
2
C)
2
0
–2
x
2
0
–2
B)
2
y
1
x
3
0
D)
y
0
–1
1
0
x
3
3
x
y
1
x
–2
E)
x
–1
1
x
y
2
–2
1
3
y
0
D)
y
0
ğıdakilerden hangisidir?
2
0
x 3
x 3
y
2
–2
f(x)
fonksiyonunun grafiği aşa-
–2
A)
y
fonksiyonu için,
–2
kilerden hangisidir?
Yanda grafiği verilen f(x)
3
x
–1
y
E)
y
2
3
0
8.
0
2
Yanda grafiği verilen f(x)
Bireysel Yetenek
–2
x
y
fonksiyonu için,
–1
10. Aşağıda verilen grafik ve fonksiyon eşleştirmelerinden hangisi yanlış verilmiştir?
3
y = - f ‡| x | - + 2
A)
fonksiyonunun grafiği aşağıdakilerden hangisidir?
0
B)
y
3
0
5
x
0 1
0
D)
y
5
2
2
x
1
E)
C)
x
–1
D)
y
–2
y
5
0
1
y
x
4
2
–2
–4
0 1
E)
y
2
0
x
f: R ® R , f(x) = |x2 – 4| + 2
f: R ® R , f(x) = x2 + |4x|
x
x
6
0 2
–4
6
f: R ® R , f(x) = x – 2|x – 3|
f: R ® R , f(x) = |x + 4| – |x|
2
2 3
–6
–4
2
C)
x
0
y
5
–1
y
4
x
1
B)
y
–4
A)
x
y
5
–2p
0
x
–p
0
f: [–2p, 2p] ® R , f(x) =
p
2p
x
|sinx| + sin|x|
2
36
1–E
2–D
3–D
4–D
5–D
6–C
7–A
8–A
9–D
10–C
Uygulama – Analiz
Soldan ve Saðdan Limit – Sonsuz Ýçin Limit ve Sonsuz Limit
lim
1.
x  3
2  5x
x 3
B) –
x 1
D) 1
A) –3
E) –5
x 1
1 x2
I.
II.
III.
IV.
V.
lim
5
 
x4
lim
1

x
x  4
x 0 
1
2
D) 
E) –
7.
I.
II.
III.
lim (2 x  3x  5)  
IV.
x 
lim
E) 
2
lim
x  0
A) –1
 2 x 13

lim   
 7  7
x
x   3 


x  5
D) –
C) 0
1
53 x
ifadesinin değeri kaçtır?
Bireysel Yetenek
3.
C) 
B) 0
B) –2
6.
ifadesinin değeri kaçtır?
A) –1
x 3
ifadesinin değeri kaçtır?
C) 
lim
2.
4x  2
x 2  6x  9
lim
5.
ifadesinin değeri kaçtır?
A) 0
Test No: 14
6x  1

x 5
V.
lim
x2
B)
2
5
C)
2
3
D) 0
E) Yoktur
5x  2

(x  2)2
1


lim  3 x  5 x  2x  4   3

x 0 


lim (1  3x  2x 3 )  
x 
lim
2x  7
 
ln x
lim
x 5

1  log3 x
x  0
x  3
Yukarıdaki eşitliklerden kaç tanesi doğrudur?
Yukarıdaki eşitliklerden kaç tanesi doğrudur?
A) 1
A) 1
B) 2
C) 3
lim
4.
x2
D) 4
E) 5
x 2  2x  5
x2
B) 1
C) –
C) 3
D) 4
E) 5
1


lim  x 2  7 2 x  3 x  5x  1

x2 


8.
ifadesinin değeri kaçtır?
ifadesinin değeri kaçtır?
A) 0
B) 2
D) 
A) 4
E) Yoktur
39
B) 3
C) 0
D) –
E) 
Uygulama – Analiz
Soldan ve Saðdan Limit – Sonsuz Ýçin Limit ve Sonsuz Limit
9.
Test No: 14
11.
y
y
f(x)
f(x)
3
2
A
O
4
x
B
–1
x
0 1
–2
Yukarıdaki şekilde, f(x) = x2 – 6x + 4a – 3 fonksiyoYukarıda y = f(x) fonksiyonunun grafiği verilmiştir.
nunun grafiği verilmiştir.
|OB| = 3.|OA| olduğuna göre, lim f(x) kaçtır?
lim f(x)  lim f(x)  lim [f(x)  2x  m]
x 1
x a
A) 45
B) 50
C) 52
D) 60
x 4
olduğuna göre, m reel sayısı kaçtır?
E) 72
A) –1
10.
x 1
B) 0
C) 1
D) 2
E) 3
3
Bireysel Yetenek
y
f(x)
2
1
–3
–2
0
1
2
3
4
x
–1
–2
Yukarıda y = f(x) fonksiyonunun grafiği verilmiştir.
12.
y
5
I. lim f(x)  lim f(x)  f(2) 
2
x 3
x 1
II.
III.
IV.
V.
3
2
lim f(x)  lim f(x)  1
x 1
x2
y = f(x)
1
lim f(x)  lim f(x)  2
x 0 
x 3
–3
–1
0
1
2
3
4
x
lim f(x)  
x 4
lim f(x)  
x 
Yukarıda y = f(x) fonksiyonunun grafiği verilmiştir.
VI.
lim f(x)  0
x 
lim [k.f(x)  1]  lim f(x)  lim f(x)  f(3)
x 1
x 1
x 3 
Grafikte verilenlere göre, yukarıdakilerden kaç
tanesi doğrudur?
A) 2
B) 3
olduğuna göre, k reel sayısı kaçtır?
C) 4
D) 5
E) 6
A) –3
B) –2
C) –1
D) 1
E) 2
40
1–C
2–E
3–D
4–E
5–E
6–B
7–C
8–A
9–A
10–C
11–C
12–E