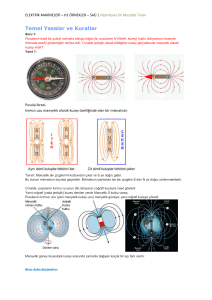
MİKRO-HİDROELEKTRİK VE RÜZGÂR SANTRALLERİ İÇİN
DÜŞÜK DEVİRLİ EKSENEL AKILI KALICI MIKNATISLI
GENERATÖR TASARIMI VE ANALİZİ
Cemil OCAK
YÜKSEK LİSANS TEZİ
ELEKTRİK EĞİTİMİ
GAZİ ÜNİVERSİTESİ
FEN BİLİMLERİ ENSTİTÜSÜ
HAZİRAN 2009
ANKARA
Cemil OCAK tarafından hazırlanan RÜZGÂR ENERJİSİ UYGULAMALARI İÇİN
DİREK
SÜRMELİ
DÜŞÜK DEVİRLİ
BİR
EKSENEL
AKILI
KALICI
MIKNATISLI GENERATÖR TASARIMI VE ANALİZİ adlı bu tezin Yüksek
Lisans tezi olarak uygun olduğunu onaylarım.
Prof. Dr. Osman GÜRDAL
……………………………….
Tez Danışmanı, Elektrik Eğitimi Anabilim Dalı
Bu çalışma jürimiz tarafından oy birliği ile Elektrik Eğitimi Anabilim dalında
Yüksek Lisans tezi olarak kabul edilmiştir.
Prof. Dr. İlhami ÇOLAK
……………………………….
Elektrik Eğitimi Anabilim Dalı, Gazi Üniversitesi
Prof. Dr. Osman GÜRDAL
……………………………….
Elektrik Eğitimi Anabilim Dalı, Gazi Üniversitesi
Yrd. Doç. Dr. Nursel AKÇAM
……………………………….
Elektrik Elektronik Mühendisliği Anabilim Dalı, Gazi Üniversitesi
Tarih:
05/06/2009
Bu tez ile G.Ü. Fen Bilimleri Enstitüsü Yönetim Kurulu Yüksek Lisans derecesini
onamıştır.
Prof. Dr. Nail ÜNSAL
Fen Bilimleri Enstitüsü Müdürü
……………………………….
TEZ BİLDİRİMİ
Tez içindeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde
edilerek sunulduğunu, ayrıca tez yazım kurallarına uygun olarak hazırlanan bu
çalışmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf
yapıldığını bildiririm.
Cemil OCAK
iv
MİKRO-HİDROELEKTRİK VE RÜZGÂR SANTRALLERİ İÇİN DÜŞÜK
DEVİRLİ EKSENEL AKILI KALICI MIKNATISLI GENERATÖR
TASARIMI VE ANALİZİ
(Yüksek Lisans Tezi)
Cemil OCAK
GAZİ ÜNİVERSİTESİ
FEN BİLİMLERİ ENSTİTÜSÜ
Haziran 2009
ÖZET
Bu tez, yüzey yerleştirmeli eksenel akılı kalıcı mıknatıslı makinaların analitik ve
sonlu elemanlar yöntemiyle tasarımına alternatif bir yaklaşım sunmaktadır.
Çalışmada eksenel akılı makinalardan tek rotor çift statorlu düzenlemenin
tasarımı üzerinde durulmuştur. Bu çalışmada geliştirilen tasarım modeli,
yüksek performanslı kalıcı mıknatıslı motorların tasarımı için tipik şart olan
kalıcı mıknatıslı yüzeylerinin karmaşık bir yapıya sahip olmasından dolayı hem
hem elektromanyetik hem de analitik tasarım içermektedir. Tek rotor çift stator
yapısına sahip eksenel akılı kalıcı mıknatıslı makina, eğer tüm tasarımlar için
aynı elektriksek yükleme, aynı hava aralığı akı yoğunluğu ve aynı akım
yoğunluğu sabit alındığında, radyal akılı kalıcı mıknatıslı makinaya göre genel
olarak daha düşük bir verime sahiptir. Fakat öte yandan eksenel akılı kalıcı
mıknatıslı makinalar, radyal akılı kalıcı mıknatıslı makinalara göre daha küçük
bir hacme sahiptirler. Özellikle radyal akılı makinalarla uzunluk oranları
(stator yığınının
uzunluğuna
karşılık
hava
aralığı
çapı)
bakımından
karşılaştırıldığında bu değer 0,5’ in altında çıkmaktadır. Karşılaştırma
sonuçları düşük kutup sayısına (p<4) sahip radyal akılı makinaların, eksenel
akılı makinalara göre daha üstün performansa sahip olduğunu göstermektedir.
v
Bilim Kodu
: 703.3.012
Anahtar Kelimeler : Mikrohes, rüzgar türbini, eksenel akılı generatör,
elektromanyetik tasarım.
Sayfa Adedi
: 124
Tez Yöneticisi
: Prof.Dr. Osman GÜRDAL
vi
DESIGN AND ANALYSIS OF LOW-SPEED AXIAL FLUX PERMANENT
MAGNET GENERATOR FOR MICROHYDROELECTRIC AND WIND
POWER PLANTS
(M.Sc. Thesis)
Cemil OCAK
GAZİ UNIVERSITY
INSTITUTE OF SCIENCE AND TECHNOLOGY
June 2009
ABSTRACT
This thesis presents an alternative approach to the analytical and FEA design of
surface-mounted axialflux permanent-magnet machines. Emphasis has been
placed on the design of axial-flux machines with a one-rotor-two-stators
configuration. The design model developed in this study incorporates facilities
to include both the electromagnetic design and analytical design of the machine
as well as to take into consideration the complexity of the permanent-magnet
shapes, which is a typical requirement for the design of high-performance
permanent-magnet motors. It is shown that an axial-flux permanent-magnet
machine with one-rotor-two-stators configuration has generally a weaker
efficiency than a radial-flux permanent-magnet machine if for all designs the
same electric loading, air-gap flux density and current density have been
applied. On the other hand, axial-flux machines are usually smaller in volume,
especially when compared to radial-flux machines for which the length ratio
(axial length of stator stack vs. air-gap diameter) is below 0.5. The Comparison
results show also that radial-flux machines with a low number of pole pairs, p <
4, outperform the corresponding axial-flux machines.
vii
Science Code : 703.3.012
Key Words
: Microhepp, wind turbine, axial flux generator, electromagnetic
design.
Page Number : 124
Advisor
: Prof.Dr. Osman GÜRDAL
viii
TEŞEKKÜR
Çalışmalarım boyunca değerli yardım ve katkılarıyla beni yönlendiren Hocam Prof.
Dr. Osman GÜRDAL’a ve yine kıymetli tecrübelerinden faydalandığım Hocalarıma
ve
beni
hiçbirzaman
yalnız
bırakmayan
çok
kıymetli
arkadaşım
İsmail
TOPALOĞLU’ na ve maddi ve manevi desteklerini hiçbirzaman esirgemeyen
ailemin değerli üyelerine teşekkürü bir borç bilirim. Tezin hazırlanması sırasında
laboratuarlarından ve fabrikalarından yararlanma imkanı sağladıkları için TEMSAN
A.Ş. (Türkiye Elektromekanik Sanayi A.Ş.) kurumuna ayrıca teşekkürü bir borç
bilirim.
ix
İÇİNDEKİLER
Sayfa
ÖZET ...................................................................................................................... iv
ABSTRACT ............................................................................................................ vi
TEŞEKKÜR ......................................................................................................... viii
İÇİNDEKİLER ........................................................................................................ ix
ÇİZELGELERİN LİSTESİ ................................................................................... xiii
ŞEKİLLERİN LİSTESİ ......................................................................................... xiv
SİMGELER VE KISALTMALAR ......................................................................xvii
1. GİRİŞ ................................................................................................................... 1
2. LİTERATÜR ÖZETİ ............................................................................................ 5
2.1 Çalışmanın Amacı ........................................................................................... 8
3. EKSENEL AKILI KALICI MIKNATISLI MAKİNALAR ................................... 9
3. 1. Eksenel Akılı Kalıcı Mıknatıslı Makinalar ..................................................... 9
3.1.1. Giriş .................................................................................................... 9
3.1.2. EAKM makinaların tipleri ve yapılar ................................................. 10
3.1.3. EAKM makina sargıları ..................................................................... 15
3.1.4. Tork üretimi....................................................................................... 18
3.1.5. Elektromanyetik tork ve EMK ........................................................... 19
4. TASARLANAN PROTOTİPTE KULLANILAN MALZEMELER .................... 21
4.1. Giriş ............................................................................................................. 21
4.2. Manyetik Malzemeler ................................................................................... 21
4.3. Kalıcı Mıknatıslarda Yön Kavramı ............................................................... 22
4.4. Domenler ..................................................................................................... 23
x
Sayfa
4.5. Yumuşak Manyetik Malzemeler ................................................................... 24
4.6. Sert Manyetik Malzemeler ........................................................................... 27
4.7. AlNiCo Mıknatıslar ...................................................................................... 29
4.8. Ferrit (Seramik) Mıknatıslar ......................................................................... 30
4.9. Azrak Toprak Mıknatıslar............................................................................. 31
4.10. Neodymium-Iron-Boron Mıknatıslar .......................................................... 32
4.11. Samaryum Kobalt (SmCo) Mıknatıslar ....................................................... 32
4.12. NdFeB ve SmCo Mıknatıslar Arasında Karşılaştırma ................................. 33
4.13. Isının Kalıcı Mıknatıs Üzerindeki Etkileri .................................................. 35
4.14. Elektriksel İletken Malzemeler ................................................................... 36
4.15. Yalıtkan Malzemeler .................................................................................. 37
5. TASARIMDA KULLANILAN KAVRAM VE YÖNTEMLER .......................... 38
5.1. Giriş ............................................................................................................. 38
5.2. Alan Hesaplama Yöntemleri ........................................................................ 38
5.2.1. Maxwell eşitlikleri.............................................................................. 38
5.2.2. İntergral eşitlikleri .............................................................................. 40
5.2.3. Kuvvet ve tork................................................................................... 41
5.2.4. Potansiyeller ...................................................................................... 41
5.2.5. Magnetostatik çözümlemeler ............................................................. 45
5.2.6. Akım modeli ...................................................................................... 48
5.2.7. Yük modeli ........................................................................................ 49
5.2.8. Sonlu farklar yöntemi ........................................................................ 50
5.2.9. Sınır elemanlar yöntemi ..................................................................... 50
xi
Sayfa
5.2.10. Yük benzetim yöntemi ..................................................................... 51
5.2.11. Sonlu elemanlar yöntemi.................................................................. 51
6. EKSENEL AKILI KALICI MIKNATISLI MAKİNALARIN TASARIMI ......... 61
6.1. Giriş ............................................................................................................. 61
6.2. Analitik Quasi-3D modelleme ...................................................................... 64
6.2.1. Manyetik eşdeğer devre ..................................................................... 67
6.2.2. Kalıcı mıknatıs kaçak akılarının hesaplanması ................................... 72
6.2.3. Hava aralığı akı yoğunluk dağılımı için analitik model....................... 75
6.2.4. Yüksüz faz gerilimi hesabı ................................................................. 79
6.2.5. Vuruntu Torku ................................................................................... 80
6.2.6. Faz direnci ve bakır kayıplarının hesaplanması .................................. 81
6.2.7. Demir kayıplarının hesaplanması ....................................................... 83
6.2.8. Kalıcı mıknatıslarda ve rotor demirinde Eddy akım kayıpları ............. 88
6.2.9. Mekaniksel kayıplar ........................................................................... 89
6.2.10. İndüktansların hesaplanması ............................................................ 90
6.2.11. Makinenin yük açısının hesaplanması .............................................. 94
6.2.12. Verim ve güç faktörü ....................................................................... 96
7. TASARLANAN MAKİNA VE SİMÜLASYON SONUÇLARI ......................... 97
7.1. İndüklenen zıt-EMK ................................................................................... 103
7.2. Vuruntu Torku ........................................................................................... 105
7.3. Verim ......................................................................................................... 105
7.4. Diğer Makina Parametreleri........................................................................ 107
7.5. Özet .......................................................................................................... 111
xii
Sayfa
8. SONUÇLAR VE ÖNERİLER........................................................................... 113
KAYNAKLAR ..................................................................................................... 115
EKLER ................................................................................................................. 119
EK-1 Prototip makina imalatında kullanılan teknik resimler .................................. 120
ÖZGEÇMİŞ.......................................................................................................... 124
xiii
ÇİZELGELERİN LİSTESİ
Çizelge
Sayfa
Çizelge 4.1. NdFeB ve SmCo karşılaştırılması ........................................................ 34
Çizelge 7.1. Prototip makinenin ana parametreleri .................................................. 98
xiv
ŞEKİLLERİN LİSTESİ
Şekil
Sayfa
Şekil 1.1. (a) Klasik tahrik sistemi: Kontrol edilen ünite dişli kutusu aracılığıyla
indüksiyon motoru tarafından tahrik edilmektedir. (b) .. Direk tahrik sistemi: Kontrol edilen ünite rotor miline direk bağlanarak (Direct Drive)
tahrik edilir ............................................................................................. 2
Şekil. 1.2. 55 kW 1500 d/dk lık kalıcı mıknatıslı senkron motor ile indüksiyon
motorunun hıza bağlı olarak verim ve güç katsayılarının
karşılaştırması ......................................................................................... 3
Şekil 3.1. Tek yanlı disk tip makina. 1- lamine stator, 2- SM, 3- rotor, 4- çerçeve,
5- mil..................................................................................................... 12
Şekil 3.2. Oluksuz statorlu çift yanlı makina. (a) dış rotorlu (b) iç rotorlu .............. 13
Şekil 3.3. Nüvesiz EASM makina. 1:.stator sargısı. 2:çelik rotor 3:Kalıcı
mıknatıslar. 4: çerçeve. 5:vidalama. 6:mil .............................................. 15
Şekil 3.4. Üç fazlı 6 kutuplu 36 oluklu tek katlı sargı ............................................. 15
Şekil 3.5. Toroidal tip sargı. 3 fazlı, 6 kutuplu, 18 sargılı ....................................... 16
Şekil 3.6. Nüvesiz üç fazlı sargı. 8 kutuplu ikiz dış rotorlu ..................................... 17
Şekil 4.1. Manyetik malzemelerin sınıflandırılması ................................................ 22
Şekil 4.2. Mıknatıslı malzemelerde enerji a) en yüksek, b) orta, c) en düşük ........... 24
Şekil 4.3. Yumuşak ve sert manyetik malzemelerin B-H eğrileri ............................. 25
Şekil 4.4. Maksimum enerjilerine göre kalıcı mıknatısların gelişim süreci............... 28
Şekil 4.5. Sıcaklığın bazı NdFeB mıknatıslarda Br’ye etkisi .................................... 38
Şekil 5.1. Bir üçgen eleman..................................................................................... 58
Şekil 5.2. İki üçgen eleman ..................................................................................... 60
Şekil 5.3. Dört üçgen eleman .................................................................................. 61
xv
Şekil
Sayfa
Şekil. 6.1. Stator boyunduruğunda ve stator dişlerinde kalıcı mıknatıs şekli ile elde
edilen akı yoğunluğu seviyesi arasındaki ilişki. (a)
bağıl mıknatıs
genişliği; stator içi yarıçapına doğru azalmaktadır.Bu durumda, dış
yarıçapta boyundurukta doyma oluşabilir.(b) bağıl mıknatıs genişliği;
statorun dış yarıçapına doğru azalmaktadır. Bu durumda, iç yarıçapta
stator dişlerinde doyma oluşabilir ......................................................... 65
Şekil. 6.2. Eksenel akılı bir makinenin 3D geometrisini quasi-3D hesaplamada
kullanılabilecek 2D bir geometriye dönüştürme metodu ........................ 66
Şekil. 6.3. wPM mıknatıs genişliği, t p kutup uzunluğu, lPM sabit kalınlık, ly
stator boyunduruğu kalınlığı ve g fiziksel hava aralığı uzunluğu
tanımlamaları.(b)’de sırasıyla; rin makine statorunun iç yarıçapı, rout dış
yarıçap ve ls; stator yığını uzunluğudur ................................................. 67
Şekil. 6.4.Bir kutup üzerindeki relüktans ağının gösterilmesi.
 y ; stator
boyunduruğunun relüktansı, Â t ; diş relüktansı, Â s ; açık oluğun
relüktansı, Â g ; hava aralığı ve fiziksel hava aralığı relüktansı, kalıcı
mıknatıs etkileri ve rotor çeliği etkilerinin toplamıdır. FPM; kalıcı
mıknatıstan dolayı ve F1; stator akımlarından dolayı oluşan mmf’dir .. 70
Şekil. 6.5. (a) Mıknatıslar stator demiri aracılığı ile kısa devre yapıldığında zigzag
kaçak akı yolları (b) Mıknatıs-rotor kaçak akısı. (c) Mıknatıs-mıknatıs
kaçak akısı. .......................................................................................... 75
Şekil. 6.6. (a) Bağıl geçirgenlik dağılımı. (b) Oluk açıklıklarının etkilerini içeren
hava aralığı akı yoğunluk dağılımı ......................................................... 78
Şekil. 6.7. Diş akı yoğunluğu dalga şekilleri............................................................ 87
Şekil. 6.8. Boyunduruk akı yoğunluk dalga şekli .................................................... 89
Şekil. 6.9. Elektriksel olarak paralel olarak bağlı iki statoru olan eksenel
akılı bir makinenin eşdeğer devresi ........................................................ 95
Şekil. 6.10. Uyarılmış senkron motorun fazör diyagramı. Endüvi reaksiyonunun
genellikle d-ekseni üzerinde demanyetize olduğu görülmektedir
I d < 0 ............................................................................................... 98
xvi
Şekil
Sayfa
Şekil. 7.1. Rotora yerleştirilen mıknatıslar ............................................................... 99
Şekil. 7.2. Tek bir mıknatısın görünümü ................................................................. 99
Şekil. 7.3. Sarımdan önce statorlardan birinin görünümü ....................................... 101
Şekil. 7.4. Sarımdan sonra statorlardan birinin görünümü...................................... 101
Şekil. 7.5. Sarımı tamamlanmış olan statorlardan birinin yaltaklandırılarak çerçevesi
içine yerleştirilmiş hali .......................................................................... 102
Şekil. 7.6. Makinanın tüm parçalarının montaja hazır halde görünümü .................. 102
Şekil. 7.7. Montajı tamamlanan makinanın görünüşü ............................................ 103
Şekil. 7.8. Makina yüksüz iken indüklenen faz gerilimleri..................................... 104
Şekil. 7.9. Makina yüklü ve kararlı durumda çalışırken indüklenen faz gerilimleri 104
Şekil. 7.10. Ölçülen vuruntu torku......................................................................... 105
Şekil. 7.11. Hızın bir fonksiyonu olarak verim değerlerinin değişimi .................... 106
Şekil. 7.12. Çıkış gücünün bir fonksiyonu olarak makinanın verimi. Anma güç
değerinden daha düşük çıkış gücü elde edilirse, verimin azalmaya
başlayacağı görülmektedir .................................................................. 107
Şekil. 7.13. Hızın bir fonksiyonu olarak çıkış gücünün değişimi. Makinanın anma
gücünün üzerindeki değerler makinanın harici bir soğutma sistemine
bağlandığı takdirde mümkün olmaktadır ............................................. 108
Şekil. 7.14. Sıcaklığın bir fonksiyonu olarak çıkış gücünün değişimi .................... 108
Şekil. 7.15. Sıcaklığın bir fonksiyonu olarak verimin değişimi .............................. 109
Şekil. 7.16. Yük altında indüklenen faz akımları ................................................... 109
Şekil. 7.17. Yük altındaki makinanın hava aralığı manyetik akı yoğunluğu ........... 110
Şekil. 7.18. Hızın bir fonksiyonu olarak mıknatıs kalınlıklarına karşılık gelen çıkış
gücü değerleri ..................................................................................... 111
xvii
SİMGELER VE KISALTMALAR
Bu çalışmada kullanılmış bazı simgeler ve kısaltmalar, açıklamaları ile birlikte
aşağıda sunulmuştur.
Simgeler
r
J
Açıklama
J cos
Stator akım yoğunluğu (A/m2)
J cor
r
E
r
B
r
H
Rotor akım yoğunluğu (A/m2)
μr
Bağıl manyetik geçirgenlik (H/m)
μ0
Boş uzayın geçirgenliği (H/m)
Φ
r
A
Manyetik akı (Wb)
E0
Yüksüz çalışma gerilimi (volt)
V1
Faz başına terminal gerilimi (volt)
x d(sat)
Tam (d) eksen kaçak reaktansı (ohm)
x sl
Kaçak reaktans (ohm)
x ad
Mıknatıslanma reaktansı (ohm)
ω
Açısal hız (rad/sn)
KW
Sargı faktörü
W
Faz başına iletken sayısı
Pelm
Elektromanyetik güç
C
Çıkış güç katsayısı
Bg
Hava aralığı akısı (Tesla)
n
Devir sayısı (d/dk)
Akım yoğunluğu vektörel (A/m2)
Elektrik alan şiddeti vektörel (V/m)
Manyetik akı yoğunluğu vektörel (Tesla)
Manyetik alan şiddeti vektörel (A/m)
Manyetik vektör potansiyeli (Wb/m)
xviii
Simgeler
Açıklama
ft
Açısal kuvvet (Nm)
p1
Kutup sayısı
li
İdeal yığın uzunluğu (m)
l fe
Aktif yığın uzunluğu (m)
τ
Kutup yayı uzunluğu (m)
Ns
Stator oyuk sayısı
N ss
Segment başına oyuk sayısı
Nc
Segment sayısı
m
Faz sayısı
a
Paralel kol sayısı
Dis
Stator iç çapı (m)
Sn
Görünür güç (KVA)
Vn
Terminal gerilimi (volt)
K fill
Oyuk doluluk katsayısı
bs
Oyuk genişliği (mm)
hs
Oyuk yüksekliği (mm)
τs
Kutup adımı (m)
By
Boyunduruk akı yoğunluğu (Tesla)
K fv
Sargı form faktörü
η HG
Hidrogeneratör verimi
Tshaft
Şaft torku (Nm)
cosφ
Güç katsayısı
la
A fazı uzunluğu (m)
lb
B fazı uzunluğu (m)
lc
C fazı uzunluğu (m)
ρcu
Bakır yoğunluğu (kg/m3)
xix
Simgeler
Açıklama
ρins
İzolasyon malzeme yoğunluğu (kg/m3)
ρ fe
Demir yoğunluğu (kg/m3)
G cu
Bakır ağırlığı (kg)
G ins
İzolasyon ağırlığı (kg)
G ys
Stator boyunduruk ağırlığı (kg)
G yr
Rotor boyunduruk ağırlığı (kg)
R yr,out
Rotor boyunduruk dış çapı (m)
R yr,in
Rotor boyunduruk iç çapı (m)
G total
Generatör ağırlığı (kg)
f
Frekans (Hz)
Dos
Stator dış çapı (m)
Kısaltmalar
Açıklama
3D
Üç boyutlu
2D
İki boyutlu
PM
Kalıcı mıknatıs
EAKMM
Eksenel akılı kalıcı mıknatıslı makina
EMK
Elektromotor kuvvet
FEM
Finite element method
IEEE
The institute of electrical and electronics engineers
IEC
International electrotechnical commission
NdFeB
Neodymium-Iron-Boron
GWh
Giga watt hour
HES
Hidro elektrik santral
kWh
Kilo watt hour
1
1. GİRİŞ
Bu çalışmada tek rotor çift stator düzenlemesine sahip eksenel akılı kalıcı mıknatıslı
makinalar üzerine durulmuştur.
Bu özel eksenel akılı kalıcı mıknatıslı makina
planlanan düşük hız yüksek tork değerlerini karşılayacak düzenlemeler içerisinde en
uygun yapıya sahip düzenlemedir. Dolayısıyla ilk olarak, statorların düzenlenerek
yerleştirilmesi kolaydır. Daha sonra, düzenlenen makina aynı anda çalışan paralel
bağlı iki bağımsız statora sahip olduğu için statorlardan birinin elektriksel olarak
devre dışı kalması durumunda diğer stator gücün yarısını temin edebilmek kaydı ile
çalışmasına devam edebilecektir. Son olarak, makina iç rotor düzenlemesine sahip
olduğundan dolayı yatakların eksenel olarak yüklenmesi küçük değerler alacaktır.
Elektrik makinaları nesiller boyunca pek çok uzman tarafından tasarlanmış, üretilmiş
ve geliştirilmiştir. Fakat günümüzde elektrik makinaları sabit bir ilerleme ve gelişme
altındadır. Bunun temel nedeni ise güç elektroniğinin hızla gelişmiş olması ve
malzeme bilimi alanında büyük yol kat edilmesidir. Motorların frekans konvertörü
vasıtası ile beslenmesi, dolayısıyla motorun kutup sayısının belirlenmesinde şebeke
frekans (50Hz) sınırlamasının olmaması makina tasarımında yeni perspektifler
açmıştır. Yeni yumuşak kompozit malzemelerin ve yüksek performanslı kalıcı
mıknatısların kullanılması makine yapılarının ve performans karakteristiklerinin
geliştirilmesine imkân sağlamaktadır.
İkinci olarak, bu alandaki eğilimler dişli kutularının olmadığı direk sürmeli tümleşik
sistemler üzerinde yoğunlaşmaktadır. Şekil. 1.1 (a)’ da klasik bir dişli kutulu tahrik
yöntemi gösterilmiştir. Şekil. 1.1 (b)’ de ise direk tahrik yöntemi kullanılan dişli
kutusuz bir tahrik yöntemi gösterilerek kabaca sistem maliyetinin ve kurulumun
gerçekleşeceği gerekli alan ifadelerinin azalacağı ifade edilmeye çalışılmıştır.
Bu nedenle, direk tahrik uygulamalarında ihtiyaç duyulan tork değeri, gün geçtikçe
tasarımda önemi hızla artan bir konu haline gelmiştir. Çünkü direk tahrikli
sistemlerde, klasik tahrikli sistemlerde olduğu gibi elektrik makinası ile kontrol
2
ünitesi arasında dişli kutusu bulunmadığından tork dalgalanmaları soğurulamayacak
ve bunun sonucunda tasarımcı makinayı tasarlarken vuruntu torkunu, makinanın
diğer performanslarını fazla azaltmaksızın olabildiğince azaltmaya çalışmalıdır.
(a)
(b)
Şekil. 1.1. Klasik ve Direk tahrikli sistemler, (a) Klasik tahrik sistemi: Kontrol
edilen ünite dişli kutusu aracılığıyla indüksiyon motoru tarafından tahrik
edilmektedir. (b) Direk tahrik sistemi: Kontrol edilen ünite rotor miline
direk bağlanarak (Direct Drive) tahrik edilir. [1]
Kalıcı mıknatıslı senkron makinalardaki gelişmeler 1983 yılında yüksek performanslı
Neodmiyum-Iron-Boron (Nd-Fe-B) mıknatısların keşfedilmesiyle birlikte oldukça
hızlı bir biçimde artmıştır. Özellikle düşük devirli ve değişken hızlı endüstriyel
uygulamalar için kalıcı mıknatıslı makinalar potansiyel uygulama alanı olarak
görülmüştür. Pek çok endüstriyel uygulamalarda indüksiyon motorları sürülen
makina için uygun hız değerini sağlayabilmek adına düşürücü dişli kutuları ile
birlikte kullanmaktadır. Elektrik motorlarını sürülen makinaya dişli kutusuz olarak
bağlamak sistem maliyetini ve makinanın sığacağı alanı azalttığı gibi sisteminde
güvenilirliğini arttırmaktadır. İstenilen yüksek performans, düşük devir ve direk
sürme fonksiyonları kalıcı mıknatıslı makina ve direk tork kontrolü (DTC) ya da
vektör kontrolü gibi yeni kontrol yöntemleri kullanılarak elde edilebilir.
Kalıcı mıknatıslı makinaların performansında verim ve güç katsayısı gibi
parametrelerin, dönüş hızından bağımsız olmasından dolayı bu makinalar düşük
devir uygulamaları için oldukça uygundur. Şekil. 1.2’ de direk tahrik ve klasik tahrik
3
yöntemlerinde kullanılan kalıcı mıknatıslı senkron motor ile indüksiyon motorunun
verim ve güç katsayısı yönünden hıza bağlı olarak karşılaştırılmaları yapılmıştır.
Şekil. 1.2. 55 kW 1500 d/dk lık kalıcı mıknatıslı senkron motor ile indüksiyon
motorunun hıza bağlı olarak verim ve güç katsayılarının
karşılaştırması.[1]
Tümleşik sistemlerde en önemli kavramlardan biri de özel uygulamalar için en uygun
elektrik makinasının seçilmesidir. Geleneksel olarak, hemen hemen tüm radyal akılı
makine tipleri kullanılmıştır. Kalıcı mıknatıslı malzemelerin gelişmesiyle birlikte,
bazı özel uygulamalar için radyal akılı makinaların kullanılması yeterli bir çözüm
olarak görülmemektedir. Eğer makinanın eksenel uzunluğu yapılacak olan
uygulamanın ihtiyaçlarına göre sınırlı ise ya da makinanın rotorunu doğrudan tahrik
edilen makinaya entegre etmek mümkün görünüyorsa eksenel akılı topoloji beklide
daha iyi bir seçim olarak karşımıza çıkabilmektedir.
Radyal akılı makinalarla karşılaştırıldığında eksenel akılı makinalar hem daha az
üretilmekte hem de daha az kullanılmaktadır. Bu yüzden eksenel akılı makinaların
4
tasarım ve üretim süreçlerinin hala gelişmekte olduğu açıktır. Radyal akılı makinalar
için üretim süreçlerini geçen yüzyılda üretilen indüksiyon makinalarının muazzam
sayısına göre dikkate aldığımızda bu üretim süreç ve yöntemlerinin yeteri kadar
gelişmiş ve iyileştirilmiş olduğunu söyleyebiliriz. Yani radyal akılı kalıcı mıknatıslı
bir motor, indüksiyon makinalarının üretim süreç ve yöntemleriyle yaklaşık olarak
aynı şekilde üretilebilmektedir.
Eksenel akılı kalıcı mıknatıslı makinaların üretimi yüksek bir yatırım gerektiren
farklı bir üretim tekniği gerektirir. Eğer üretilecek makina sayısı da düşük bir miktar
ise bu seferde makinanın birim güç başına maliyeti artacaktır. Bu makina yapılarının
klasik radyal akılı yapılardan farklı olması, üretimi için gerekli olan yöntemlere
yönelik yüksek yatırım gerektiren bir süreci içermesi gibi sebeplerden dolayı eksenel
akılı makinalar hem üretim teknikleri bakımından hem de tasarımına yönelik
çalışmalar bakımından önümüzdeki yıllarda bu alanda en çok gelişme gösterecek
makina türlerinden biridir.
5
2. LİTERATÜR ÖZETİ
Elektrik makinalarının tarihi ilk makinaların eksenel akılı olduklarını gösterir.
M.Faraday 1831, “kalıcı mıknatıslı” başlıklı olan isimsiz gelişimler 1832, W.Ritchie
1833, B.Jacobi 1834 bunlara örnek olarak gösterilebilir. Ancak kısa bir süre sonra T.
Davenport 1837 de elektrik makinalarının ana yapılandırması olarak geniş bir alanda
kabul edilecek olan geleneksel radyal akılı makinalar için ilk patenti istedi [2].
Belirli bir ilkesi olmayan, ilkel çalışan ilk eksenel akılı makina 1831 yılında M.
Faraday tarafından kayıtlara geçirilmiş ve Faraday’ın disk makinası olarak
adlandırılmıştır. Elektrik makinalarının disk tipi olanı aynı zamanda N. Tesla’nın
ABD’den aldığı 405858 numaralı patentinde de görülmektedir. Bunların uzun süre
rafa kaldırılmalarına neden olan etkenleri kısaca şu şekilde özetleyebiliriz.
• Stator ve rotor diskleri arasında güçlü bir magnetik çekim.
• Oluk yapımı, nüvenin laminasyon olarak üretimi gibi fabrikasyon güçlükleri.
• Nüvenin laminasyon yapımının pahalı oluşu.
• Düzgün bir hava aralığı sağlamanın güçlüğü.
Her ne kadar kalıcı mıknatıs uyarımının elektrik makinalarına uygulanması
1830’ların başlarına dayansa da sert magnetik malzemelerin zayıf kalitesi bunların
kullanımını azaltmıştır. 1931’de Alnico’nun, 1950’de Baryum Ferrit’in ve özellikle
1983’te NeFeB malzemenin bulunması kalıcı mıknatıs uyarmalı sistemin yeniden
canlanmasını sağlamıştır.
İlk yapılan elektrik makinalarında uyarma alanı kalıcı çelik mıknatıs ile elde
edilmekteydi. 1866 yılında Siemens tarafından kendi kendine uyarılan doğru akım
jeneratörünün yapılması büyük elektrik makinalarının üretimine geçişi sağlamıştır.
1940’lı yıllarda AlNiCo alaşımlı kalıcı mıknatısların bulunması yeniden kalıcı
mıknatıslı makinaların yapımına yol açmıştır [3].
6
1950’lerde Baryum, Stronsiyum ya da Kurşun’un demir-oksitle oluşturduğu ferrit
mıknatısların bulunması ve geliştirilmesi bu mıknatısların elektrik makinalarında
kullanımına yol açmıştır.
Mıknatıs uyarmalı ilk motor 1900’de Edison tarafından gerçekleştirilmiş olup
1935’de AlNiCo mıknatısların bulunması ile ilk mıknatıslı senkron generatör
tasarımları ortaya çıkmıştır [3].
Ferit mıknatısla uyarılmış ilk senkron makina 1962’de W.Volkrod tarafından
gerçekleştirilmiştir [4]. Campbell (1974), “Pancake” olarak adlandırılan d.a.
motorunu fan sürücüsü olarak sunmuş ve eksenel akılı kalıcı mıknatıslı d.a.
makinasının prensiplerini ortaya koymuştur. Burada Faraday’ın diski olarak işaret
ettiği eksenel akılı elektrik makinasının özellikle kalıcı mıknatıslardaki gelişmeler
gibi birkaç avantaja rağmen hala sınırlı olarak kullanıldığı belirtilmiştir.
Çalışmasında otomobil radyatör soğutması ve otomobil tekerleğini sürmek üzere
sunduğu motorun hali hazırda bir teorisinin olmadığını da belirtmiştir. Campbell
(1975), Eksenel akılı makina için magnetik devre çözümlemesini yapmıştır. Chan ve
ark. (1980), Eksenel akılı makinalar için yeni bir yaklaşım ortaya koymuştur.
Campbell ve ark. (1981), Eksenel akılı kalıcı mıknatıslı makinaları büyük çapta yeni
uygulama alanları için incelemiş ve en iyileştirme için bilgisayar yazılımı
gerçekleştirmiştir. D’Angelo ve ark. (1983), Üç boyutlu sonlu elemanlar
çözümlemesini bu makinalar için sunmuştur [5].
Chan C.C. , Bahsedilen makinalar için tasarım ve uygulama çalışması yapmıştır [6].
Nasar ve Xiong, Magnetik şarj kavramını kullanarak disk makinanın alan hesabını
yapmıştır [7]. Spooner ve Chalmers, “TORUS” olarak adlandırılan oluksuz ve
toroidal statorlu, eksenel akılı senkron makinayı tasarlamışlardır [8]. Chalmers ve
Spooner, Tıkız makina incelemesini yapmışlardır [9]. Chalmers ve ark, Torus
generatörü modelleyip benzeşimini yapmışlardır.[10] Benzeşimde PSpice, mıknatıs
olarak ise NdFeB kullanılmıştır. Zhilichev üç boyutlu çözümsel modeli bu makinalar
için geliştirmiştir. 2D ve 3D çözümlemesi arasında karşılaştırma yapmış ve temel alt
7
bölgelerde integral dönüşümü ve fourier yöntemleriyle hassas sonuçlar elde etmiştir
[11].
Huang ve ark, Elektrik makinalarının karşılaştırılması için boyut ve güç yoğunluğu
denklemlerini düzenlemişlerdir [12]. Muljadi ve ark, Rüzgâr türbin uygulamaları için
toroidal sargılı eksenel akılı kalıcı mıknatıslı generatör tasarlamışlardır. Bu generatör
direk sürmeli ”direct-drive” olarak yapılmıştır [13]. Tareg ve ark, Yüksek hızlı kalıcı
mıknatıslı eksenel akılı generatörler için modüler tasarımı gerçeklemiştir. Generatör
50 kVA, 420 V, 5000 rpm ve 3 fazlıdır [14].
Mbidi ve ark, İki modüllü eksenel akılı makinanın mekanik tasarım kriterlerini
ortaya koymuşlardır [15]. Aydın ve ark, Oluklu ve oluksuz statorlu torus tip eksenel
akılı yüzey montajlı kalıcı mıknatıslı disk makinaların tasarım ve elektromagnetik
alan çözümlemesini yapmışlardır [16]. Stapati ve Krishnan, Radyal ve eksenel akılı
kalıcı mıknatıslı fırçasız makinaların performans karşılaştırmasını yapmışlardır [17].
Braid ve ark, Çok modüllü eksenel akılı kalıcı mıknatıslı senkron makinaların
tasarım, çözümleme ve geliştirilmesini yapmışlardır.[18] Bumby ve ark, Eksenel
akılı kalıcı mıknatıslı makinaların elektromagnetik çözümlemesini gerçeklemişlerdir
[19]. Gieras, 2004’te eksenel akılı kalıcı mıknatıslı fırçasız makinaların genel bir
incelemesini kitap olarak yayınladı [20]. Kalıcı mıknatıslı eksenel akılı makinalar
üzerine yapılmış araştırma ve incelemeleri bu şekilde özetledikten sonra tasarım
yöntemleri üzerine yapılan çalışmaları özetleyebiliriz.
8
2.1 Çalışmanın Amacı
Bu çalışmanın ana amacı analitik ve sonlu elemanlar analizleri ile rüzgâr türbini ve
mikro ölçekli hidroelektrik santral uygulamaları için eksenel akılı kalıcı mıknatıslı
direk sürmeli bir generatör tasarlamak ve uygulamasını gerçekleştirmektir.
Kullanılan analitik hesaplama yöntemi ve elde edilen boyutlandırma parametrelerine
göre ilgili modelin üç boyutlu bir sayısal çözümleme programında modellenerek,
elektromanyetik parametrelerinin elde edilmesi uygulaması yapılacak olan generatör
için bir ön tasarım niteliğindedir. Ayrıca, literatürde yapılan taramalar sonucunda
yüzey yerleştirmeli eksenel akılı kalıcı mıknatıslı makinaların analitik tasarımına
yönelik pek çok yayın olmasına rağmen bu yayınlarda ifade edilen yöntem ve
hesaplamalar
farklı
geometrilerdeki
makinalara
uyarlanabilir
nitelikte
ve
karmaşıklıkta değildir. Bazı kitap ve yayınlarda yüzey yerleştirmeli eksenel akılı
kalıcı mıknatıslı makinaların boyutlandırılması statorun ortalama yarıçapına endeksli
olarak yapılmış fakat mıknatıs şekli karmaşık bir yapıya sahipse, bu durumda kayda
değer bir yanlışlık yapılacağı açıktır. Bu tez de eksenel akılı kalıcı mıknatıslı
makinaların
mıknatıs
geometrileri
karmaşık
bir
yapıya
tasarlanabilmesine yönelik analitik bir yöntem açıklanmıştır.
sahip
olsa
dahi
9
3. EKSENEL AKILI KALICI MIKNATISLI MAKİNALAR
3. 1. Eksenel Akılı Kalıcı Mıknatıslı Makinalar
3.1.1. Giriş
Eksenel Akılı Kalıcı Mıknatıslı Makinalar (EAKMM) dairesel yapıda olanlara göre
disk şekilleri, kompakt üretimleri ve yüksek güç yoğunlukları gibi nitelikleri
nedeniyle oldukça ilgi çekici özelliklere sahiptir. Bunlar Disk makinalar olarak ta
adlandırılırlar. Motor olarak yapılanları özellikle elektrikli araçlar, pompalar, fanlar,
vana kontrolleri, santrifüjler, makine elemanları, robotlar ve endüstriyel ekipmanlar
için uygundur.
Eksenel akılı kalıcı mıknatıslı makinalar küçük ölçekli güç üretimi için de
kullanılmaktadırlar. Çok kutuplu yapılabilmelerinden dolayı rüzgâr türbinleri gibi
düşük
devir
uygulamalarında
çok
idealdirler.
Geleneksel
model
ile
karşılaştırıldıklarında eksenel akılı makinaların ortaya çıkan belli başlı üstünlükleri
şu şekilde sıralanabilir [6].
• Yüksek verim
• Manyetik nüvenin yüksek kullanım oranı
• Düşük frekanslarda büyük kutup sayıları ile tıkız (kompakt) olarak yapılabilmeleri
• Mikro-Üretim üniteleri için imalat kolaylığı
• Ekonomik oluşları
• Bakır kullanım faktörünün yüksekliği
• Yüksek hızlardaki gürültünün azaltılabilirliği
• Düşük birim maliyetli enerji üretilebilirliği
• Yüksek güvenirlik ve az bakım
Tek bir stator ve rotordan oluşmaları bunların çoklu olarak yapılabilmeleri ile değişik
yapılarda değiştirilebilmelerini olanaklı kılar. Çoğu durumda hacim, kütle, güç
10
transferi ve zaman kullanımı gibi etkenleri en iyileştirmek için, rotorlar güç iletim
parçası olarak kullanılır. Özellikle elektrikli araçlar ile pompa uygulamalarında
asansör, fan ve diğer tip makinalarda rotor bu şekilde çift görev üstlenir.
Eksenel akılı kalıcı mıknatıslı makinaların yapımları açısından bakıldığında tek yanlı
ya da çift yanlı, oluklu ya da oluksuz nüveli, rotor ortada ya da dışarıda yapılı,
mıknatıslar gömülü veya yüzeye yapıştırmalı ve tek modüllü ya da çoklu modüllü
olmak üzere çok değişik yapılarda tasarlanabilirler.
Bunlar özetle aşağıdaki biçimde maddelenebilir;
.
• Eksenel akılı tek hava aralıklı (tek stator, tek rotor)
• Eksenel akılı çift hava aralıklı (iki rotor arasında tek stator veya tersi)
• Eksenel akılı oluksuz statorlu tek hava aralıklı
• Çok hava aralıklı (Çoklu stator ve rotor düzenekleri)
• Eksenel akılı oluksuz statorlu çift hava aralıklı [16].
3.1.2. EAKM makinaların tipleri ve yapılar
Prensip olarak eksenel akılı makinaların her bir tipi, disk tip makinaların değişik bir
sürümü olacaktır. Pratikte disk biçimindeki bu makinalar şu üç çalışma şekli ile
sınırlanmışlardır;
Fırçasız D.A. motoru
Eksenel Akılı Kalıcı Mıknatıslı Makinaların yaygın olarak kullanıldıkları
modellerden birisi de doğru akım fırçasız motorlardır. Çağımızın en büyük
sorunlarından birisi olan hava kirliliğini önlemek için uygulanan birçok yöntemden
birisi de elektrikle çalışan otomobiller üretmektir. Ancak bu araçlar, yüksek maliyet,
düşük güç yoğunluğu ve akü guruplarının uzun şarj süreleri gerektirmeleri nedeniyle
marketlerde yaygın olarak satılır hale henüz gelmemiştir [9].
11
Melez araçlarda en önemli sorun araç içerisinde bu düzenek için yeterli yer
bulunamamasıdır. İşte bu nokta da eksenel akılı kalıcı mıknatıslı motorlar en iyi
çözümdür. Gerçekten de eksenel akılı kalıcı mıknatıslı makinalar diğer geleneksel
indüksiyon, DA ve Radyal akılı kalıcı mıknatıslı makinalarla karşılaştırıldığında
yüksek bir tıkız özelliğe sahiptir. Ayrıca ağırlık ve hacim bakımından da oldukça
avantajlı bir özelliğe sahiptir. Rotor akımları olmadığından verimleri yüksektir.
Taşıma amacıyla kullanılan bu makinalar yüksek hız ve moment sağlama özelliğine
sahiptir.
Eksenel akılı kalıcı mıknatıslı her makina, tıpkı silindirik olanlardaki gibi mil dönüşü
ile senkronize olarak stator sargılarını değişken frekanslı dönüştürücü üzerinden
beslemek suretiyle fırçasız da motor olarak kullanılabilir. Elektronik güç
dönüştürücüleri akım dalgalanmalarını sınırlayacak şekilde tasarlanmalıdır.
A.A. generatör
Kalıcı mıknatıslı generatörler yıllardır rüzgâr türbinlerinde kullanılmaktadır. Çoğu
küçük rüzgâr türbin üreticileri direk sürmeli (direct-drive) kalıcı mıknatıslı generatör
kullanırlar.
Rüzgâr türbinleri için tasarlanacak generatör düşük maliyet, hafiflik, düşük hız,
yüksek moment ve değişken hız üretim koşullarını sağlamalıdır. Kalıcı mıknatıs
olarak NdFeB veya Ferrite mıknatıs kullanılabilir. Generatör bir, iki veya üç fazlı
olarak yapılabilir. Stator sargıları toroidal olarak sarılır. Rüzgâr kulelerinin
gereksinimlerini azaltmak için generatör hafif olmak zorundadır. Rüzgâr
santrallerinin düşük döner hızda çalışmalarından dolayı generatör çok kutuplu
yapılır. Rotor nüvesinde mıknatısların değiştirilebilmesi için yeterli alana sahiptir.
Hava aralığı yoğunluğu rotor çapından bağımsız olarak ayarlanabilir. EAKM
Generatör modüler olarak üretilip istenildiğinde bu modüler eksenel olarak
eklenebilir ve toplam generatör gücü artırılabilir.
12
D.A. generatör
Torus yapı tasarımı; düşük gerilim dalgalanmalı, tıkız düşük gerilim D.A. generatör
olarak kullanım için özellikle iyi bir tasarımdır. Stator disklerinin ve nüvesinin
gerektirdiği incelik kutup sayısı ile ters orantılıdır. Altı ve daha büyük kutup
sayılarında makina uzunluğu ve kütlesi küçük tutulur.
Tek yanlı EAKM makinalar
Eksenel akılı makinaların tek yanlı yapılandırılmaları çift yanlı olanlara göre daha
basittir ancak tork üretim kapasiteleri daha düşüktür. Şekil 3.1’de tipik tek yanlı
yüzey mıknatıs yapıştırmalı rotorlu, elektromekaniksel çelik şeritten laminasyon
statorlu EAKM makina görülmektedir [20]. Bunlar endüstride, taşıma ve servo
elektromekanik sürücülerde kullanılır.
Şekil 3.1. Tek yanlı disk tip makina. 1- Stator laminasyonu, 2- KM, 3- rotor,
4- çerçeve, 5- mil
Çift yanlı iç rotorlu EAKM makinalar
Kalıcı mıknatıslı iç rotorlu çift yanlı EAKM makinalarda sargılar stator nüvesine
yerleştirilirler. Kalıcı mıknatıslı disk iki stator arasında döner. Kalıcı mıknatıslar
rotora gömülür ya da yüzeyine yapıştırılır. Manyetik olmayan hava aralığı çok
büyüktür. Statorları paralel bağlı çift yanlı makinanın stator sargılarının birisi kopsa
da çalışabilir. Diğer taraftan eksenel çekim kuvvetlerine zıt ve eşit olan bir akı
ürettiğinden seri bağlantı tercih edilir [20].
13
Çift yanlı oluksuz iç statorlu EAKM makinalar
Yüzük biçiminde iç statorlu bu makinalarda ferromanyetik stator nüvesi çok fazlı
oluksuz endüvi sargılarını (drum tip sargı) taşır. Bu makinada yüzük halkası
biçimindeki stator yapısı çelik şeritlerin sürekli sarımından veya çelik tozlarının
preslenmesinden yapılır. Toplam hava aralığı, yalıtkanla birlikte stator sargılarının
kalınlığı, mekaniksel açıklık ve eksenel yönde mıknatıs kalınlıklarının toplamına
eşittir. Çift yanlı makinalar kısaca ikiz rotor olarak adlandırılırlar. İç ve dış rotorlu
yapılar şekil 3.2’de verilmektedir [21].
Çok büyük hava aralıkları nedeniyle maksimum akı yoğunluğu 0.65 Tesla’yı
geçemez. Bu miktarda bir akı yoğunluğu temin etmek için büyük hacimlerde kalıcı
mıknatıs kullanmaya gereksinim duyulur.
Şekil 3.2. Oluksuz statorlu çift yanlı makina. (a) dış rotorlu (b) iç rotorlu.
Çift yanlı oluklu iç statorlu makinalar
Yüzük biçimindeki stator oluklu olarak ta yapılabilmektedir. Bu tip motorlar için
oluklar, sargıların içlerinden geçmesine izin verecek şekilde çelik nüve içerisine
düzgünce delinerek açılırlar. Bu durumda hava aralığı 1 mm’nin altında
yapılabilmekte ve hava aralığı manyetik akısı 0.85 Tesla’yı aşabilmektedir. Önceki
tasarıma nazaran mıknatıs hacmi %50 azalmaktadır.
14
Çift yanlı nüvesiz iç statorlu makinalar
Nüvesiz statorlu EAKM makinalar manyetik ve elektriksel iletkenliği olmayan
taşıyıcı bir yapı üzerinde sarılmış stator sargılarına sahiptirler. Histerisiz ve eddy
akım kayıpları gibi nüve kayıpları yoktur. Kalıcı mıknatıslar ve rotor kütlesel
diskteki kayıplar göz ardı edilebilir. Bu tasarım biçimi yüksek verim ve sıfır tork
titreşimi sunar. Lamine edilmiş stator nüveli yapı ile karşılaştırıldığında hava aralığı
akısı için daha büyük boyutta kalıcı mıknatıs kullanımı gerektirir. Stator sargıları
karşılıklı olarak rotora yerleştirilmiş mıknatısların oluşturduğu alan içine konmuştur.
Şekil 3.3. Nüvesiz EAKM makina. 1:.stator sargısı. 2:çelik rotor. 3:Kalıcı
mıknatıslar. 4: çerçeve. 5:vidalama. 6:mil [20].
3.1.3. EAKM makina sargıları
Sargıların taşıması gereken özellikler;
• Özellikle sargı uçlarının dış kısımlarında iletken geçişi olmamalı ya da en az
olmalı
• Oluklarda en yüksek bakır kullanım faktörünü sağlamalı
• Moment salınışlarını azaltmak için mmk dağılımını sinüsoidal olarak üretmeli
15
• Sargı faktörü generatör gücünü azaltmayacak kadar yüksek olmalı
İnce iletken ve dağıtılmış paralel iletkenler kullanılması durumunda bakır teller
içerisinde üretilen eddy akım kaybında bir azalma olacaktır [22].
Oluklarda dağıtılmış üç fazlı sargılar
Tek katlı sarımda bir oluğa yalnızca bir sargı kenarı yerleşir. Tüm sargıların sayısı
oluk sayısının yarısına eşittir. Bu durumda faz başına düşen sargı sayısı C= S/2m,
dir. (S: oluk sayısı, m: faz sayısı). Çift katlı sargılarda her olukta farklı sargı kenarları
bulunur ve toplam sargı sayısı oluk sayısına eşittir. Şekil 3.4 tek katlı 36 oluklu sargı
örneği vermektedir.
Şekil 3.4. Üç fazlı 6 kutuplu 36 oluklu tek katlı sargı [20].
Drum tip (toroidal) sargılar
Drum tip stator sargılar çift yanlı, ikiz rotorlu EAKM makinalarda kullanılır.
Sarımların her fazı stator nüvesindeki olası akı sirkülâsyonlarını bertaraf edecek
biçimde eşit sayıda seri bağlı sargılara sahiptir. Sargılar birbirlerine zıt biçimde
diametrik olarak dağıtılırlar. Toroidal olarak da adlandırılan drum tip sargıların
16
avantajları kısa uç uzunluğu basit stator nüvesi ve faz sayılarının kolay tasarımıdır.
Şekil 3.5 Toroidal sargı tipine ait bir örnek vermektedir.
Şekil 3.5. Toroidal tip sargı. 3 fazlı, 6 kutuplu, 18 sargılı [20].
Nüvesiz stator sargıları
Nüvesiz stator sargılar ikiz rotor çift yanlı EAKM makinalarda kullanılmaktadır.
Yapım kolaylığı için stator sargıları normal olarak trapez biçiminde tek katlı
sarımlardan oluşur. Statorun yapımı sargı uçlarının belirli açılarla kıvrılmasıyla elde
edilir.
Böylece aktif iletkenler eşit olarak aynı düzleme yayılırlar. Sargılar epoksi reçine ve
sertleştiriciyle tutturulurlar. Açıkça görülmektedir ki oluklu sargılar için hazırlanan
sarımlar doğrudan oluksuz stator için kullanılabilir. Sadece oluk terimi yerine sarım
kenarı terimi kullanılır.
Nüvesiz statorda kullanılan diğer bir sargı profili ise Rhomboidal sargı tipidir. Bu
trapez olana göre daha kısa uç bağlantısına sahiptir. Rhomboidal sargı tipinde
17
sargının aktif kenarları soğutma amacıyla statorda su kanalı açmaya izin verir. Şekil
3.6 nüvesiz üç fazlı sargıya, Şekil 3.7 ise Rhomboidal sargıya ait bir örnek
vermektedir.
Şekil 3.6. Nüvesiz üç fazlı sargı. 8 kutuplu ikiz dış rotorlu [20]
Şekil 3.7. Rhomboidal sargı [20].
18
3.1.4. Tork üretimi
Eksenel akılı makinalarda tork üretimi boyutların yarıçapın bir fonksiyonu olması
nedeniyle elektromanyetik tork yarıçap boyunca süreklidir ve silindirik olanlardaki
gibi sabit değildir. Eksenel akılı makinaların kutup adımı ve kutup genişliği yarıçapın
bir fonksiyonudur. Bunlar sırasıyla şu eşitliklerle verilir.
τ=
2πr πr
=
p
2p
b p = α iτ = α i
αi =
Bavg
Bmg
=
(3.1)
πr
p
bp
τ
(3.2)
(3.3)
Kutup adımı ve genişliği yarıçapın fonksiyonu iken αi parametresi normalde
yarıçaptan bağımsızdır. Aynı zamanda hat akımı da yarıçapın fonksiyonudur. Hat
akım yoğunluğunun tepe değeri,
Am (r ) =
m1 2 N1 I a
πr
Son olarak üretilen elektromanyetik tork;
(3.4)
19
dTd = rdFx = r[k w1 A(r ) Bavg dS ] = 2πα i k w1 A(r ) Bmb r 2 dr
(3.5)
A(r) hat akımı stator sargılarının, oluklara dağıtılmış olduğu durumda statorun tek
aktif yanının ya da nüvesiz veya iç drum sargı tipi olması durumunda da tüm statorun
elektriksel yüklemesidir.
3.1.5. Elektromanyetik tork ve EMK
Yukarıda da bahsedilen gibi eksenel akılı makinaların ortalama Elektromanyetik
tork’u 2πα i k w1 A(r ) Bmb r 2 dr Do/2 den Di/2’ ye kadar yarıçap r için integralini
alırsak ortalama elektromanyetik tork şu şekilde yazılır.
1
1
2
2
2
2
Td = α i m1 I a N1k w1 Bmg ( Do − Di = α i m1 N1k w1 Bmg Do − (1 − k d ) I a
4
4
(3.6)
Burada;
kd=Ri/Ro =Di/Do
Ortalama tork manyetik akıya göre yeniden yazılabilir. Buna göre,
Td = 2
p
π
m1 N1k w1Φ f I a
(3.7)
Sinüsoidal akım ve manyetik akı yoğunluğu için rms tork;
Td =
m1
pN 1k w1Φ f I a
2
(3.8)
20
Boş çalışmada emk, manyetik akı dalga biçiminin birinci harmoniğinin türevi
alınarak bulunur.
dΦ f 1
= 2πfN 1k w1Φ f cos wt
(3.9)
E f = 2πfN1k w1Φ f = 2πpN1k w1Φ f ns
(3.10)
e f = N1k w1
dt
21
4. TASARLANAN PROTOTİPTE KULLANILAN MALZEMELER
4.1. Giriş
Elektrik makinalarının tasarımında çok sayıda malzeme kullanılmaktadır. Bunlar
manyetik malzemeler, elektriksel iletken malzemeler ve yalıtkan malzemeler olmak
üzere üç temel grupta toplanabilirler. Her ne kadar bilinen konular olsalar da,
özellikle kalıcı mıknatısların devamlı gelişme göstermelerinden dolayı ayrıntılı
olarak incelenmelerine gerek görülmüştür. Bu noktada internet üzerinden değişik
üretici firmaların internet sayfaları incelenerek varılan teknolojik gelişmelerin en son
noktalarının sunulmasına özen gösterilmiştir.
4.2. Manyetik Malzemeler
Manyetik
malzemeler,
Diamanyetik,
Paramanyetik,
Ferromanyetik,
Antiferromanyetik ve Ferrimanyetik olmak üzere beş grupta sınıflandırılırlar.
Diamanyetik malzemeler net atomik veya moleküler manyetik momente sahip
değildirler. Bu malzemelere bir alan uygulandığında alana zıt yönde akım üretirler.
Paramanyetik malzemeler atomik derecede net manyetik momente sahiptirler fakat
komşu momentler arasındaki kuplaj zayıftır. Bu momentler bir alan uygulanmasıyla
aynı hizaya gelirler ancak bu hizaya gelme dereceleri termal uyarmanın rastgele
etkisiyle yüksek sıcaklıklarda azalır [5].
Ferromanyetik malzemeler atomik derecede net bir manyetik momente sahiptirler
ancak paramanyetik malzemelerden farklı olarak komşu momentler arasında güçlü
bir kuplaj vardır. Bu kuplaj domenler olarak adlandırılan mikroskobik bölgelerde
momentlerin kendiliğinden aynı hizaya gelmelerini artırır. Domenler bir alan
uygulamasıyla
karşılaştığında
daha
güçlü
bir
hizalanmaya
yönelirler.
Antiferromanyetik ve Ferrimanyetik malzemeler komşu momentlerinin biri diğerine
ters paralel biçimde yönlendirilmiş atomik momentlere sahiptir. Antimanyetik
22
malzemelerde komşu momentler eşittir ve net bir manyetik moment yoktur.
Ferrimanyetik malzemelerde komşu momentler eşit değildir ve net bir moment vardır
[23]. Malzemelerin bu manyetik özelliklerinin şematik görünümleri Şekil 4.1’de
verilmektedir.
Paramanyetik
Antiferromanyetik
Ferromanyetik
Ferrimanyetik
Şekil 4.1. Manyetik malzemelerin sınıflandırılması
4.3. Kalıcı Mıknatıslarda Yön Kavramı
İlk üretilen mıknatıslarda, manyetik özellikler yöne bağlı değildi. Yani mıknatısların
manyetik özellikleri bütün yönlerde hemen hemen aynı idi. Bu tür mıknatıslar eş
yönlü (isotropic) mıknatıslar olarak adlandırılırlar. Eş yönlü mıknatıslar küçük güçlü
uygulamalarda kullanılabilir olsalar da, bu daha küçük kalıcı mıknatısiyet ve enerji
üretimi anlamına geldiğinden oldukça pahalı olan malzemelerin verimsiz olarak
kullanılması demektir. Araştırmalar sonucunda, manyetik özelliklerin belirli bir
yönde yoğunlaştırılması ile mıknatısların daha etkin duruma gelmesi sağlanmıştır.
Elde edilen bu mıknatıslar, eş yönsüz (anisotropic) mıknatıslar olarak adlandırılırlar.
Mıknatısların yönlendirilmesi amacı ile en yaygın olarak kullanılan yöntem,
manyetik malzemenin bir manyetik alan içinde tavlanması ve böylece atomların alan
etkisi ile yönlendirilmesidir. Manyetik eş yönsüz bir malzeme manyetik özellik
bakımından farklı yönlerde farklılıklar gösterir. Eş yönsüzlüğün prensip olarak
sınıflandırması şöyle yapılabilir.
23
•
Magnetokristalin eş yönsüzlük
•
Şekil eş yönsüzlük
•
Stres eş yönsüzlük
•
Değiştirme eş yönsüzlük
Bunlardan magnetokristalin ve şekil olanı mıknatıslanma sürecinde önemli rol oynar.
Magnetokristalin eş yönsüzlüğün en temel biçimi eş eksenel eş yönsüzlüktür. Şekil
eş yönsüzlük malzemenin temel bir özelliği değildir. Daha çok malzemede
demagnetizasyonun geometrik yapıdan dolayı oluşan yönsel bağımlılığıdır.
4.4. Domenler
Yukarıdaki bölümlerde belirtildiği gibi ferromanyetik malzemelerde atomik moment
çiftlerin curie sıcaklığı altlarında kendi kendine gruplaşma eğilimlerinde artma olur.
Böylece ferromanyetik malzemelerin oda sıcaklığında manyetik olarak doyuma
ulaşacağı beklenebilir. Bununla birlikte bu malzemelerin sık sık mikroskobik
derecede mıknatıslanmadığını görürüz. Bu ancak manyetik domenler kavramıyla
açıklanabilir [5].
Domenler tipik olarak 1012-1015 atom içerirler. Domenlerdeki atomik momentler
tam olarak tercih edilen kristal grafik eksenler doğrultusunda gruplaşmayı sağlayan
magnetokristalin eş yönsüzlüğün etkisinde kalırlar. Böylece domen içerisindeki
momentler birbirlerine paralel uzanırlar ve domen manyetik doymanın yerel
bölgelerini temsil eder. Bir malzemenin büyük hacimli bir örneği boyut, şekil ve yön
içerisinde değişiklik gösteren çok sayıda domenlerden oluşur. Örnek malzemenin
mıknatıslanması tüm bu domenlerin yapısal ve yönsel olarak toplanması şeklinde
tanımlanır. Homojen malzemelerde domenler toplam enerjiyi en az edecek
biçimdedirler.
Örneğin
Şekil
4.2’de
görülen
blok
malzemelerden
(a)
konfigürasyonunda magnetostatik enerji en yüksek, (c) konfigürasyonunda ise en
düşüktür. Komşu domenler birbirlerinden domen duvarı olarak adlandırılan geçiş
katmanlarıyla ayrılırlar.
24
Şekil 4.2. Mıknatıslı malzemelerde enerji (a) en yüksek, (b) orta, (c) en düşük
4.5. Yumuşak Manyetik Malzemeler
Ferromanyetik malzemelerin mekanik dayanıklılığının arttırılması ve manyetik
özelliklerin iyileştirilmesi için yıllarca süren çalışmalar sonucunda manyetik
özelliklerinin dayanıklılığı açısından iki farklı tür ortaya çıkmıştır. Eğer bir
mıknatısın manyetik özellikleri kolaylıkla bozulabiliyorsa, bu tür malzemelere
yumuşak (soft) manyetik malzemeler adı verilir. Özellikle ilk yapay mıknatıs
türlerinden olan çelik mıknatıslar genellikle yumuşak mıknatıslardır. Bu mıknatıslar
aynı zamanda mekanik açıdan da yumuşaktırlar.
Yumuşak mıknatıslar bir takım ısıl işlemlerden geçirilerek, manyetik özelliklerinin
daha kalıcı olması sağlanmıştır. Manyetik özelliklerini kolaylıkla kaybetmeyen
malzemeler sert (hard) manyetik malzemeler olarak isimlendirilirler. Mıknatıslara
uygulanan bu tür ısıl işlemlerin bir amacı da mıknatısın mekanik açıdan
sertleştirilmesidir. Sonraki yıllarda, manyetik açıdan sert, mekanik açıdan yumuşak
olan özel amaçlı mıknatıslar da geliştirilmiştir. Yumuşak malzemeler kendini kolay
magnetize ve demagnetize ettiren yüksek geçirgenlikli ve düşük koersiviteli
(Hc<1000A/m) olarak karakterize edilirler. Sert malzemeler ise, kendilerini daha zor
magnetize ve demagnetize ettiren nispeten düşük geçirgenlik ve yüksek koersiviteye
(Hc>10000A/m) sahiptir. Bu iki malzeme arasındaki fark en iyi olarak histerisiz
eğrilerini karşılaştırarak gösterilebilir. Yumuşak manyetik malzemeler elektrik
makinalarında manyetik devre olarak kullanılırlar. Bu malzemelerden beklenen
25
özellik, olabilecek en yüksek geçirgenlik ve akı yoğunluğu ile en az çekirdek
kaybıdır [5].
Yumuşak malzemeler akı yollarını sınırlayıcı ve bir bölgedeki akı yoğunluğunu
artırmak amacıyla kullanılırlar. En yaygın olarak kullanılan yumuşak malzemeler;
yumuşak demir, demir-slikon alaşımları, nikel-demir ve yumuşak ferritlerdir. Bunlar
trafolar, roleler, motorlar, indüktörler ve elektromıknatıslar gibi birçok cihazda
kullanılırlar.
Yumuşak
bir
malzeme
seçilirken
onun
geçirgenliği,
doyma
magnetizasyonu, direnci ve koersivitesi gibi özellikleri ön plana çıkar. Yüksek
geçirgenlik ve magnetizasyon akı yükseltme ve odaklama için istenir. Direnç ve
koersivite yüksek frekans uygulamalarında önemlidir. Yüksek bir direnç eddy
akımlarını düşürürken, düşük koersivite histerisiz kayıplarını azaltır. Yumuşak
malzemeler manyetik olarak B-H eğrilerinin geçirgenliğinin sabit olduğu yerlerinde
doğrusaldırlar. Geçirgenliğinin H’a bağımlı olduğu(μ=μH) diğer durumlarda ise
doğrusal değildirler. Şekil 4.3 yumuşak ve sert manyetik malzemelerin histerisiz
eğrilerinin karşılaştırmasını vermektedir.
Şekil 4.3. Yumuşak ve sert manyetik malzemelerin B-H eğrileri
Yumuşak demir elektromanyetik uygulamalar ve DA elektromıknatısların çekirdek
malzemesi olarak yaygın biçimde kullanılmaktadır. Ancak AA uygulamalarında
yerlerini düşük eddy akımı kayıpları nedeniyle yüksek dirençli malzemelere
bırakmaktadırlar. Ticari olarak elde edilebilen tipik bir yumuşak demir düşük katkı
malzemesi içerir. (%0,02 karbon, %%0,035 manganez, %0,015 sülfür, %0,002 fosfor
ve silikon). Bu şekildeki bir alaşıma sahip yumuşak demir 80 A/m koersiviteye,
26
1.7x106 A/m doyma mıknatıslanmasına ve 10000 maksimum geçirgenliğe sahiptir.
Bununla birlikte bu özellikler katkıları ortadan kaldıran hidrojen içerisinde demirin
tavlanmasıyla da geliştirilebilir. Bu işlem koersiviteyi 4 A/m’ye düşürebilir ve
maksimum bağıl geçirgenliği ise 100000’e çıkarabilir.
Yumuşak demire düşük yüzdelikte bir silikon eklenmesiyle direnci artar, koersitif
kuvveti azalır ve manyetik kararlılığı gelişir. %3 silikon eklenmiş bir demir
alaşımının saf demire göre direnci 4 kat artar. Ancak silikonun varlığı doyma akı
yoğunluğunda keskin bir azalmaya neden olur. Ayrıca %5’ten daha fazla silikon
eklenmesi demiri daha kırılgan yapar ve üzerinde çalışmayı oldukça zorlaştırır.
Ticari malzemelerde bu oran %3,4 ile sınırlanmıştır [24].
Silikon pahalı bir malzeme olmamasına karşın silikonlu demir çok pahalıdır. SilikonDemir malzemelerde düşük kayıplar ve yüksek geçirgenlik elde etmek için gerekli
koşullar şu şekilde sıralanabilir.
Eddy akımlarını azaltmak için;
•
Yüksek alaşım içeriği
•
Küçük tanecik boyutu
•
İnce malzeme
•
İyi imalat
Histerisiz kayıplarını azaltmak için;
•
İnce malzeme
•
Düşük alaşım derecesi
•
Büyük tanecik boyutu
•
Düşük yüzey deformasyonu
27
Yüksek geçirgenlik için;
•
Düşük alaşım içeriği
•
Düşük yüzey boyutu
•
İyi imalat
•
Yüksek saflık
Yumuşak manyetik malzemeler manyetik devre relüktansını azaltmak için yüksek
geçirgenlik, demir kısımların hacim ve ağırlıklarını azaltmak için yüksek akı
yoğunluğu ile verimi yükseltmek için düşük kayıp istenen elektrik makinalarında
kullanılırlar. Pratikte bunların hepsinin aynı anda tek bir malzeme ile karşılanması
her zaman olanaklı değildir [5].
Elektriksel çelikler yönlendirilmemiş ve yüzey yönlendirilmiş olmak üzere iki tiple
sınıflandırılmışlardır. %0 - %-3 arasında silikon içeren yönlendirilmemiş elektriksel
çelikler esas olarak eş yönlüdürler. 1,3 metre genişliğe kadar 0,35 ve 0,8 mm
kalınlıkları arasında şerit biçiminde üretilirler. Bu şerit genellikle katmanlar arasında
yalıtımı sağlamak amacıyla ince bir yalıtıcı yüzeyle kaplanır. Bu tür çelikler elektrik
mühendisliğinde lamine çelik olarak bilinirler.
Nikel-demir alaşımlar endüktörler, manyetik yükselteçler ve ses frekans trafolarının
çekirdeklerinde olduğu gibi değişik uygulamalarda kullanılırlar. Ticari olarak elde
edilebilen Ni-Fe alaşımlar %50-80 Ni içerirler ve çok yüksek geçirgenlikli olarak
karakterize edilirler [5].
4.6. Sert Manyetik Malzemeler
Sert manyetik malzemelerin yüksek koersivite ve düşük geçirgenlik özellikleri
onların magnetize ve demagnetize olmalarını zorlaştırır. Bu tür malzemeler bir kez
mıknatıslanıp ondan sonra uzun süre bu mıknatıslanmalarını korumalarından dolayı
kalıcı mıknatıslar olarak adlandırılırlar. Kalıcı mıknatıslar elektronik ev eşyaları,
28
bilgisayarlar, veri depolama cihazları, elektromekanik cihazlar, telekomünikasyon
donanımları ve biyomedikal aletleri de içeren çok geniş bir uygulama yerlerinde alan
kaynağı olarak kullanılırlar [23].
Mıknatıs seçiminde en öncelikli özellikler, elde edilebilecek alanın kararlılığı ve
genliğidir. Bunlar koersivite Hc, doyma mıknatıslanması Ms ve kalıcı mıknatıslık
Br’yi içerir. Bunlar histerisiz eğrisinin ikinci çeyreği olan ve demagnetizasyon eğrisi
olarak bilinen alanla ilgilidirler. –Hc<H<0 Aralığında elde edilebilecek en büyük BH değerinin sağlanabildiği nokta tanımlanır. Bir mıknatıs alan kaynağı olarak
kullanıldığında demagnetizasyon eğrisi üzerinde bir çalışma noktasında polarize olur.
Bu çalışma noktası kullanılan devreye bağlıdır. Bu devrenin yük doğrusundan elde
edilebilir. Bu çalışma noktasının bulunması mıknatıs boyutunu ve maliyetini düşürür.
Kalıcı mıknatıslar normalde demir, nikel ve kobalt gibi elementlerin alaşımlarından
oluşur. Kalıcı mıknatıslı malzemelerin yıllara göre gelişimi Şekil 4.4’te
verilmektedir. Kalıcı mıknatıslar büyük B-H eğrilerine, yüksek kalıcı mıknatısiyete
(Br) ve yüksek mıknatıslanmayı giderici Hc kuvvetine sahiptirler.
Şekil 4.4. Maksimum enerjilerine göre kalıcı mıknatısların gelişim süreci [5].
29
Kalıcı mıknatıslar kimyasal yapılarına göre üç temel grupta toplanabilirler. Bunlar;
AlNiCo, seramik (Ferrit), ve Azrak-Toprak mıknatıslardır.
Bunlar ayrıca yapılış biçimlerine göre alt sınıflandırılmalara da ayrılırlar. Diğer
mıknatıslar metalik iletken olmalarına karşın Ferrit olanlar (mıknatıssal olarak güçlü
seramik), elektriksel ve ısısal olarak yalıtkandırlar. AlNiCo’lar nispeten yüksek
remenans ve düşük koersif kuvvete sahiptirler. Seramikler düşük remenans ve
oldukça yüksek koersiviteye sahiptirler. Buna karşın bu iki parametre Azrak toprak
mıknatıslarında yüksek değerlere sahiptir. Seramikler çok ucuz ve bol olan ham
malzeme kullanırlar.
4.7. AlNiCo Mıknatıslar
Alnico alaşımlar 1930’lu yılların başlarına dayanır. Bunların temel bileşenleri demir,
kobalt, nikel, alüminyum ile az miktarlarda da bakır ve bazı diğer metallerden
oluşmaktadır. Bunlar soğuk çalışmalarda çok kırılgan olacak kadar serttirler. Üretim
yöntemleri sıvı alaşımların dökümü veya metal tozların preslenerek sıkıştırılması ile
sınırlıdır.
İlk işlem olarak Al-Ni-Fe-Co malzemeleri etrafındaki ince manyetik parçacıkların ısı
ile kontrollü olarak çökelmesini sağlamaktır. Bu parçacıklar, bittiğinde yüksek
koersiviteye sahip ve eş yönsüz olarak şekillendirilmiş olarak uzatılır ve filiz
biçimine çevrilir.
Alinco’ların eş yönlü ya da eş yönsüz olabileceği şekil verme süreci boyunca
manyetik parçacıkların yönlendirilip yönlendirilmediklerine bağlıdır. Bunlar yüksek
kalıcı indüksiyon ve yüksek sıcaklıklara karşı son derece büyük direnç gösterirler ve
nispeten yüksek enerji üretirler. Bununla birlikte birçok durumda kullanımları düşük
koersif kuvvetleri nedeniyle sınırlanır. Preslenmiş AlNiCo, döküm olandan daha ince
yapılabilirken süper mekanik karakteristikler gösterir. Döküm AlNiCo mıknatıslar
atmosfer kontrollü toz metalürji işlemiyle üretilirler. Gerçek şeklini alabilmesi için
30
yüksek sıcaklık kullanılır(1100-1300 Co). Bunlar ağırlık olarak 0.05 – 150 g
arasındadır.
Diğer
kalıcı
mıknatıslarla
karşılaştırıldığında
AlNiCo’lar
şu
karakteristikleri gösterir.
•
Tam yoğunluğa yakınlık.
•
İnce kristal metalik yapı.
•
Yüksek sıcaklık kararlılığı.
•
İyi korozyon dayanımı.
•
Yüksek mekanik dayanım.
AlNiCo malzemeler düşük koersif kuvvetlerinden dolayı kolayca demagnetize
edilebilirler ve bundan dolayı dikkatli kullanılmalıdırlar. AlNiCo5 için uzunluk/çap
oranı en az 5/1 olmalıdır. Eğer karmaşık şekiller veya küçük boyutlar gerektiğinde bu
koşullar sağlanamazsa AlNiCo8 malzemesi kullanılmalıdır.
Bu manyetik özelliklerine bakıldığında oldukça etkileyicidirler ancak zayıf fiziksel
özelliklere sahiptirler. Daha önceden de belirtildiği gibi çok kırılgan olmaları
üretilmiş bir mıknatısı kullanırken çok sabırlı ve masraflı bir işlem gerektirirler [5].
4.8. Ferrit (Seramik) Mıknatıslar
Sert Ferit’ler en ucuz ve en yaygın olarak kullanılan kalıcı mıknatıs malzemelerdir.
Ferit mıknatısların gelişimi 1950’lere gitmektedir. Mıknatıslar XO.6(Fe2O3)
biçimindeki bileşimin ince tanecikli tozlarından üretilir. Burada X Baryum,
Stronyum veya Kurşundan biridir. İnce parçacıklar halinde öğütülmüş metalurjik
metotları kullanarak üretilirler ve genellikle seramik olarak adlandırılırlar. Üretim
süreci Fe2O3 bileşiminin baryum, stronyum ya da kurşun dan birinin karbonatıyla
birlikte ıslak ya da kuru olarak uygun oranda hazırlanmasıyla başlar. Karışım 1000–
1350 Co sıcaklıkları arasında ısıtılarak toz haline getirilir. Toz haline getirilen
malzeme ezilip öğütülerek ince pudra taneleri haline getirilir. Eş yönlü mıknatıslar
ince pudra taneciklerinin istenilen biçimde kurutularak ve preslenerek üretilirler ve
31
son olarak 1100-1300 Co de ısıtılarak kütle haline getirilirler. Eş yönsüz ferrit
mıknatıslar tane boyutu (yaklaşık 1μm) tek domenli parçacıkların kullanılmasıyla
üretilir. Toz taneleri suyla birlikte bir harç oluşturacak şekilde karıştırılır ve bu harç
sonra preslenir ve sonra katılaştırılır. Tozlara basınç uygulama süreci boyunca
yönlendirme alanı uygulanır [5].
Katılaşma süresince toplam büzülme miktarı % 15’tir. Bitmiş mıknatıslar katılaşmış
malzemenin parlatılmasıyla son ürün haline gelirler. Bu çeşit mıknatıslar diğer azrak
toprak mıknatıs olmayanlarla karşılaştırıldıklarında daha yüksek manyetik akı
yoğunluğu, daha yüksek koersif kuvvet ve demagnetizasyon ile oksidasyona karşı
daha yüksek dayanıma sahiptirler. Bu tür mıknatısların en büyük avantajları düşük
maliyetli oluşlarıdır.
Bu yüzden çoğu kalıcı mıknatıs uygulamalarında fazlaca tercih edilirler. Seramik
yapılarından dolayı ferrit mıknatıslar çok sert ve kırılgandırlar. Bunlar için özel
makina teknikleri kullanılmalıdır. Sert Ferrit mıknatıslar yönlendirilmiş ve
yönlendirilmemiş olarak üretilebilirler. Yönlendirilmiş olanlar Ferrit parçaların
yüksek magneto-kristalin şekilli yönsüz parçalarından elde edilirler. Ferrit parçaların
fiziksel yönlendirilmeleri presleme işlemi gerektirir. Sert Ferrit mıknatıslar
mükemmel bir korozyon dayanımına sahiptirler ve -400 C0 ile 2500 C0 arasında
çalışabilme yeteneğine sahiptirler. Sıcaklık arttıkça remanans %0.2 azalır, koersivite
ise %0.3 artar. Çok düşük sıcaklıklarda düşük çalışma noktalı manyetik sistemlerde
kalıcı demagnetizasyon riski vardır.
4.9. Azrak Toprak Mıknatıslar
Azrak Toprak elementler atom sayıları 58–71 arasında bulunan geçiş grubu
elementleridir. Ticari olarak kullanılabilen en güçlü kalıcı mıknatıs malzemedirler.
Bunlar Neodymium-Iron-Boron (NdFeB) veya Samarium-Cobalt (SmCo)’dan
birinden oluşturulur
32
4.10. Neodymium-Iron-Boron Mıknatıslar
NdFeB mıknatısların gelişimi SmCo mıknatısları takip eder ve 1980’lere kadar gider.
Gelişimlerinin artmasını en çok motive eden olgu maliyetlerindeki etkin avantaj
nedeniyle SmCo olanlara tercih edilmesidir. Ayrıca Neadymium, Cobalt’tan çok
daha fazla bulunmaktadır [23]. Azrak-Toprak, mıknatıs tasarımda yeni bir çığır açan
geliştirilmiş bir manyetik malzemedir. Diğer manyetik malzemelerin çok ötesinde
düşük boyut ve ağırlıklarda yapılabilmeye izin veren manyetik özelliklere sahiptirler.
Neadymium Iron Boron mıknatıslar iki neadymium atomu, ondört demir atomu ve
bir boron atomuna sahip tipik bir azrak toprak alaşımıdır. Böylece kimyasal yapısı
Nd2Fe14B şeklinde olup yaygın olarak NdFeB olarak kullanılır. Koersiviteyi
artırmak,
düşük
oksidasyon
karakteristiğini
kazanmak
ve
diğer
benzer
karakteristikler için bazı diğer elementlerde vardır. Bu elementler uyarıcı (dope)
alaşım olarak kullanmak olup ağırlıkça %10’un altındadır NdFeB, tozları
azaltma/yayılma süreci ve hızlı sulama yöntemlerini de içeren değişik işlemler
kullanılarak üretilir. Ürün eş yönlü veya eş yönsüz olabilir. Preslenmiş NeodymiumIron-Boron mıknatıs yönlendirme-presleme-sıkıştırma yöntemi ile üretilir(orientpress-sinter-OPS).
Sıkıştırılmış NdFeB mıknatıslar toz metalürjik işlevle biçimlendirilirler. Bu
mıknatıslar kalıpla veya izostatik olarak preslenebilir. Presleme süreci boyunca
manyetik alanlar mıknatısın manyetik performansın en iyileştirilmesine yardımcı
olacak şekilde uygulanır. Daha sonra preslenmiş mıknatıslar sıkıştırılmak için
koruyucu atmosfer altında fırına konurlar. Yüzey kaplaması genellikle NdFeB
mıknatıslarda kullanılır. Koruyucu katman olarak çinko ve nikel yaygınca kullanılır.
Aynı amaçla kadmiyum kromat, alüminyum kromat, ve epoksi de kullanılabilir [5].
4.11. Samaryum Kobalt (SmCo) Mıknatıslar
SmCo mıknatıslar 1960’larda gelişmeye başlamıştır. Bunların gelişimi demir, kobalt
ve nikel gibi geçiş serisi ferromanyetik elementler olan Azrak-Toprak elementlerin
33
alaşımlarının araştırılmasına yönelme sonucunu doğurmuştur. SmCo mıknatısların
iki temel bileşimi Sm1Co5 ve Sm2Co17 dir. Birinci SmCo mıknatıslar SMCO
tozlarının bir reçine içerisinde birleştirilmesiyle oluşturulur. Tamamlanmış son ürün
alaşımın azaltma/eritme veya azaltma/yayılma süreçlerinden biri temeline dayanır.
Azaltma/eritme yönteminde Sm ve Co karıştırılır ve alaşım biçimini alacak şekilde
eritilir. Döküm alaşım kırılır ve kolayca öğütülerek toz tanecikleri haline dönüşür.
Azaltma/yayılma sürecinde samaryumoksit (Sm2O3) ve kobalt tozları yaklaşık 1150
Co de kalsiyumla birlikte reaksiyona tabi tutulur ve aşağıdaki biçim aldırılır;
10Co + Sm2O3 + 3Ca = 2SmCo5 + 3CaO , 3CaO denklemden değişik işlemler
uygulanarak ayrılır. SmCo mıknatısların maliyeti NdFeB mıknatıslardan daha
yüksektir. SmCo mıknatısların en büyük avantajı 300 Co ye kadar yüksek
sıcaklıklarda kullanılabiliyor olmasıdır. Bunlar yüksek koersivite ve BH eğrisinin
ikinci çeyreğinde doğrusal özellikleri ile karakterize edilirler [5].
4.12. NdFeB ve SmCo Mıknatıslar Arasında Karşılaştırma
NdFeB ve SmCo mıknatısların her ikisi de sıkıştırılarak ya da polimer bağlı
mıknatıslar olarak yapılabilirler. Döküm azrak-toprak mıknatıslar, vakum altındaki
tozların dökümü ile sağlanan toz metalürji işlevi ile üretilirler. Mıknatıslar büyük
bloklar halinde üretilebilirler veya bileşenler preslenerek birbirlerine dikiş gibi
eklenirler. Kaplamaları kullanılacakları çevrenin gereklerine göre seçilebilir.
Samarium - Cobalt korozyon ve sıcaklığa karşı Neodymium’dan daha fazla direnç
gösterdiğinden kaplama gerektirmez [5].
NdFeB mıknatıslar SmCo mıknatıslardan daha yüksek bir maksimum enerji (BHmax)
üretme yeteneğine sahiptirler. NdFeB’nun BHmax’ı 30 MGO ya kolayca ulaşabilir ve
55 MGO ya kadar çıkabilir. Nd-Fe-B mıknatıslar özellikle 80 Co nin altındaki
sıcaklıklardaki çalışma yerleri gibi çoğu ortamlarda Sm-Co mıknatıslar yerine
kullanılır.
34
NdFeB’ nun sıcaklık kararlılığı Sm-Co kadar iyi değildir. NdFeB’nun manyetik
performansı 180 Co nin üzerindeki sıcaklıklarda hızla bozulur. SmCo mıknatıs ile
karşılaştırıldığında NdFeB nun korozyon ve oksidasyon dayanımı nispeten düşüktür.
Çizelge 4.1 NdFeB ve SmCo mıknatısların karşılaştırılmasını vermektedir.
Çizelge 4.1. NdFeB ve SmCo karşılaştırılması [5].
4.13. Isının Kalıcı Mıknatıs Üzerindeki Etkileri
Mıknatısların manyetik özelliklerini değiştiren bir etken de ortam sıcaklığıdır.
Yüksek sıcaklıklarda, uzun süre belirgin bir sıcaklık düzeyinin üstünde bulunma
durumunda, mıknatıs malzemenin mıknatıslanmasını engelleyebilecek metalürjik
35
değişimler oluşabilir. Bu metalürjik değişim sıcaklığının yanı sıra, mıknatısın kalıcı
mıknatıslığın sıfırlandığı, ancak metalürjik değişiklik olmadıkça üstüne çıkıldığında
mıknatıslanmanın yeniden olanaklı olduğu Curie sıcaklığı da tanımlanmıştır.
Sıcaklığın bazı NdFeB mıknatıslarda Br’ye olan etkisi Şekil 4.5’te verilmektedir.
Şekil 4.5. Sıcaklığın bazı NdFeB mıknatıslarda Br’ye etkisi [5].
4.14. Elektriksel İletken Malzemeler
Bu malzemelerin olabilecek en yüksek iletkenlik ve en düşük direnç katsayısına
sahip olmaları gerekmektedir. Bunların aynı zamanda tel, bobin ve komütatör
dilimleri gibi üretimler için mekanik dayanıma da sahip olmaları gerekmektedir.
Bakır, alüminyum ve bakır alaşımları gibi elektriksel iletken malzemeler düşük
dirençli devre elde etmede kullanılırlarken, elektriksel karbon malzemeler fırça
olarak kullanılırlar.
4.14.1. Bakır ve alaşımları
Bakır işlenmesi son derece kolay bir elementtir. Genellikle elektrik makinalarında
yuvarlak tel olarak kullanılırlar dikdörtgen olanları 500 V’un altındaki gerilimlerde
pek kullanılmamaktadırlar. Da ve Aa elektrik makinalarının komütatör dilimlerinde
de bakır kullanılabilmektedir. Saf bakırın elektriksel ve termal iletkenliği sadece
gümüş ile artırılabilir. Bu yüzden gümüş dışındaki tüm metallerle olan alaşımları
36
daha düşük bir iletkenliğe neden olur. Saf bakıra kalay, kadmiyum, berilyum ve diğer
metallerin düşük yüzdelerde karışımı mekanik özelliklerin artmasını sağlarken
elektriksel direnci de saf bakıra göre yükseltir.
4.14.2. Alüminyum alaşımları
Alüminyum bakırdan hafif ve ucuz olup erime sıcaklığı da düşüktür. Dolayısıyla
dökümü daha kolaydır. Buna karşın saf alüminyumun iletkenliği bakırın ancak %60’ı
kadardır ve mekanik dayanımı düşük olup ince iletken olarak yapılamazlar. Elektrik
makinalarında alüminyum kullanılması küçük makinaların kafes çubuklarında
olmaktadır.
4.15. Yalıtkan Malzemeler
Yalıtkan malzemeler yüksek dielektrik, yüksek direnç ve yüksek ısıl iletkenlik
özellikleriyle karakterize edilirler. Bu malzemeler elektrik makinalarının çeşitli
gerilim değerlerinde akım taşıyan değişik kısımları ile oluklar arasında ısı dağılımını
engellemeyecek şekilde yalıtımı sağlamak amacıyla kullanılırlar. Elektrik makinaları
enerji dönüşümü yapan makinalar olup bu süreç boyunca enerji kayıpları oluşması
kaçınılmazdır.
Kayıplar öncelikle makinanın aktif parçalarında, manyetik devrelerinde demir veya
çekirdek kayıpları ve elektrik devresinde bakır kayıpları olarak ortaya çıkar.
Makinada ki kayıplar ısı enerjisi olarak ortaya çıkar ve makinanın demir ve bakır
kısımlarındaki sıcaklığın artmasına neden olurlar. Bu yüzden kayıplar sadece verim
ile ilgili olmayıp sargı sıcaklıklarının yükselmesi açısından da oldukça önemlidir.
Elektrik makinalarında kullanılan demir ve bakır gibi aktif parçalar yalıtım amacıyla
kullanılan gereçlere göre daha yüksek bir sıcaklığa dayanabilirler. Her ne kadar
spesifik elektriksel ve manyetik yüklemenin azaltılması makinadaki kayıpları ve ısı
artışını azaltsa da bu ekonomik değildir. Daha iyi bir tasarım tüm aktif parçaları tam
olarak kullanmak ve yetenekli yalıtım ile soğutma sistemi geliştirmektir. Sentetik
37
reçine ve diğer plastik malzemelerdeki son gelişmeler elektrik makinalarının
boyutlarına önemli etki yapmıştır.
38
5. TASARIMDA KULLANILAN KAVRAM VE YÖNTEMLER
5.1. Giriş
Bu bölümde, üzerinden çalışılan eksenel akılı kalıcı mıknatıslı makinanın tasarım ve
analizinde kullanılan temel kavramlar olarak alan hesaplamalar ve hesaplamalarda
günümüzde yaygın olarak kullanılan sayısal yöntemler üzerinde durulmuştur.
Bu makinaların tasarımında kullanılan yöntemler iki ana unsurdan oluşmaktadır.
Bunlardan birincisi, sonlu elemanlar yöntemi ile alan hesaplamaları yapan sayısal
çözümleme paketleridir ve bu paketlerin kullanmış olduğu sayısal yöntemlerdir.
İkincisi ise analitik hesaplama yöntemlerinin kullanılıp deneysel sonuçlarla elde
edilen değerlerin kıyaslanmasıdır.
5.2. Alan Hesaplama Yöntemleri
5.2.1. Maxwell eşitlikleri
Elektromanyetik alanlar yük ve akım kaynaklarından doğar ve Maxwell eşitlikleri ile
kullanılır.
Fark biçimindeki alan eşitlikleri;
G
G
∂D
∇×H = J +
∂t
(5.1)
G
∇⋅B = 0
(5.2)
G
G
∂B
∇×E = −
∂t
(5.3)
39
G
∇⋅D = ρ
(5.4)
G
Burada serbest akım yoğunluğu J (A/m2), serbest yük yoğunluğu ρ (C/m3) kaynak
G
G G G
terimleri olup H , B , E , ve D vektörel büyüklük olarak alanlardır. Bu dört alan
büyüklüğünün her biri üç bileşene sahiptir. Alan eşitliklerinin komple teorisi yapısal
ilişkiler biçiminde ele alınan aşağıdaki ek bağımsız eşitliklerle genişletilmek
zorundadır [5].
G
G G
B = μ 0 (H + M)
(5.5)
G
G G
D = ε0E + P
(5.6)
Sabit, doğrusal, homojen ve eş yönlü durumlarda bu yapısal ek eşitlikler aşağıdaki
şekilde sadeleştirilebilir.
G
G
B = μH
(5.7)
G
G
D = ε0E
(5.8)
G
G
J = σE
(5.9)
G
Serbest akım yoğunluğu J serbest yüklerin hareketi sonucu oluşur. Bir iletken
malzemenin içinden akan elektronların hareketi iletim akımı, yarı iletkenler içindeki
elektron ya da boşlukların hareketi iletim akımı, sıvılar içindeki pozitif veya negatif
iyonların yer değiştirmesi elektrolitik akım ve vakum içindeki iyon ya da
elektronların hareketi yayınma akımı olarak nitelenir [23].
40
5.2.2. İntergral eşitlikleri
Alan eşitlikleri yukarıda olduğu gibi fark eşitlikleri ile ifade edilebildiği gibi integral
eşitlikleriyle de yazılabilir. İntegral eşitlikleri genellikle yüksek dereceli geometrik
simetrinin bulunduğu uygulamalar için çok daha kullanışlıdır.
G
G
∂B
v∫ c E ⋅ dl = − v∫s ∂t ⋅ ds
G
G
G ∂D
v∫c H ⋅ dl = v∫s (J + ∂t ) ⋅ ds
(5.10)
(5.11)
Diverjans eşitliklerinin S kapalı yüzeyli V hacminde integralini alır ve diverjans
teoremini uygularsak eşitlikler aşağıdaki durumu alırlar.
v∫s
G
B ⋅ ds = 0
G
v∫s D ⋅ ds = v∫ v ρ ⋅ dv
(5.12)
(5.13)
5.11 eşitliği Amper’in devre kuramının genelleştirilmişidir ki buna göre, herhangi
kapalı bir yol etrafında manyetik alan şiddetinin sirkülasyonu yüzey boyunca akan
serbest akıma eşittir. 5.10 eşitliği Faraday’ın elektromanyetik indüksiyon yasasını
temsil eder. Buna göre sabit kapalı bir devrede indüklenen elektromotor kuvvetinin
durumu devreyi halkalayan manyetik akıların artış oranının negatif değerine eşittir.
En sade hali ile bu kuram bir E alanının manyetik akının zamanla değişiminden
üretildiğini ifade eder. Faraday kanunu trafolar, generatörler ve elektromekanik
41
cihazlar gibi birçok önemli aygıtların davranışları için temel teşkil eder. S yüzeyi
boyunca B vektör alanının akısı aşağıdaki biçimde tanımlanır.
G
Φ = v∫ B ⋅ ds
s
(5.14)
5.2.3. Kuvvet ve tork
Elektromekanik çözümlemeler için sürekli akımla ilgili olan Kuvvet ve Tork’un
G
G
bilinmesine gereksinim vardır. Bunu elde edebilmemiz için E ve B alanlarıyla
oluşturulan bölgedeki q yüklerinin u hızıyla hareket etmesindeki davranışları
incelememiz gerekir. Çok iyi bilindiği gibi hareketli yükler değeri aşağıda verilen
Lorentz kuvvetlerini doğururlar.
G
G
F = q(E + u × B)
(5.15)
G
Biz özellikle B alanı tarafından oluşturulan sürekli akımın neden olduğu tork ve
G
kuvvet ile ilgilenmekteyiz. J akım yoğunluğu dağılımında Lorentz kuvveti ve tork
G
sırasıyla şu şekilde bulunabilir. V, J akım yoğunluğunun oluştuğu hacim r ise
tork’un hesaplandığı noktaya olan vektör iken,
G G
F = ∫ J × B ⋅ dv
(5.16)
G G
T = ∫ r × (J × B)dv
(5.17)
v
v
kuvvet ve tork sırasıyla eşitlik 5.16 ve 5.17 ile ifade edilir.
42
5.2.4. Potansiyeller
Maxwell eşitlikleri alanlar için direk çözülebilir. Ancak alanların potansiyeller
kullanılarak elde edilmesi genellikle daha uygundur. Özellikle skaler ve vektörel
G
potansiyeller A ve φ için değişkenlerin değişimi kullanılarak ikinci derece
eşitliklerden bağımsız değişkenlerle birinci dereceli eşitliklerden dört adet yazılabilir.
Potansiyeller için ikinci derece eşitlikler;
G
G
G
∂ 2A
∇ A − με 2 = −μJ
∂t
2
∇ 2ϕ − με
∂ 2ϕ
∂t
2
=−
(5.18)
ρ
ε
(5.19)
ile ifade edilir. Bu eşitliklerin çözümü;
G '
'
G
μ J(x , t − x − x / u) '
A(x, t) =
dv
4π ∫v
⎡x − x' ⎤
⎣
⎦
(5.20)
'
'
1 ρ(x , t − x − x / u) '
ϕ(x, t) =
dv
4πε ∫v
⎡x − x' ⎤
⎣
⎦
(5.21)
u = 1/ με
ε = ε0
μ = μ0
u = c = 1/ μ 0ε0 = 3 × 108 m / s
43
Quasi-Statik teori
Quasi-Statik alan teorisi elektromanyetik dalga boyuna oranla ufak olan bölgelerde
alçak frekanslarda uygulanır. Quasi-Statik teori elektriksel devre çözümlemesi,
elektromekanik cihazlar ve eddy akım konularını da içeren uygulamalarda önemli bir
yer tutar.
Matematiksel perspektiften bakıldığında quasi-statik yaklaşım yer değişim akım m
G
terimi olan ∂D ∂t ’nin alan eşitliklerinde ihmal edilmesini kullanır. Bu göz ardı etme
G
yapıldığında yani ∂D ∂t =0 iken alan eşitlikleri aşağıdaki biçimi alır.
G G
∇×H = J
G
∇⋅B = 0
G
G
∂B
∇×E = −
∂t
G
∇⋅D = ρ
(5.22)
G
Yukarıdaki ilk iki eşitlikte zamanın bir türevi yoktur. Böylece akım yoğunluğu J ’nin
G
G
zamana bağlı olduğu durumlarda H ve B alanları statik sistemler için çözümlenir.
Üçüncü eşitlik elektromekanik uygulamalarda önemli rol oynayan faraday
kanunudur.
Statik teori
Statik alan teorisinde zaman değişkeni yoktur. Buna rağmen bu sınırlayıcı teori
elektrostatik ve magnetostatik gibi çok geniş alanlarda uygulanma olanağı bulur.
Magnetostatik teori sürekli mıknatıs uygulamalarında yaygın olarak kullanılır.
G
G
∂D ∂B
=
=0
∂t
∂t
(5.23)
44
Statik alan teorisinde Maxwell eşitliklerinin zaman bağımlı terimleri göz ardı edilir.
Bu durumda alan eşitlikleri aşağıdaki gibi manyetostatik ve elektrostatik olmak üzere
ikiye ayrılır.
G G
∇ × H = J,
G
∇ × B = 0 Manyetostatik
G
∇ × E = 0,
G
∇ × D = ρ Elektrostatik
(5.24)
Manyetostatik teori
Manyetostatik çözümleme için eşitlikler aşağıdaki biçimde özetlenebilir.
G G
∇ × H = J,
v∫ c
G
∇ ⋅ B = 0 Diferansiyel biçim
G
G
H ⋅ dl = v∫ J.ds,
s
v∫s
G
B ⋅ ds = 0 int egral biçim
G
G G
B = μ0 (H + M) Tamamlayıcı ilişki
(5.25)
(5.26)
(5.27)
Manyetostatik eşitlikler alanlar için doğrudan çözülür. Bununla birlikte vektör
G
potansiyel A kullanılarak elde edilmesi daha uygundur.
Elektrostatik teori
Elektrostatik çözümleme için eşitlikler aşağıdaki biçimdedir.
G
∇ × E = 0,
v∫ c
G
E ⋅ dl = 0,
G
∇⋅D = ρ
diferansiyel biçim
v∫s D ⋅ ds = ∫v ρ ⋅ dv
int egral biçim
(5.28)
(5.29)
45
G
G G
D = ε0 E + P
(5.30)
Alanlar elektrostatik eşitliklerin direk çözümünden elde edilebilir. Alanlar aynı
zamanda skaler potansiyel φ kullanılarak da çözümlenebilir [5].
5.2.5. Manyetostatik çözümlemeler
Vektör potansiyel
Alanların vektör potansiyel A ile çözümlenmesi doğrudan çözümlerine göre daha
uygundur. Tüm sadeleştirmeler yapıldıktan sonra vektör potansiyel eşitlikler şu
şekilde özetlenebilir [23].
G '
G
G
G
G
G
μ
J(x )
∇ A = −μJ ⇒ A (x) =
⇒
=
∇
×
⇒
dv
B
A
4π ∫v x − x '
2
G
μ
⇒ B(x) =
4π ∫v
G '
J(x )x(x − x ' )
x−x
'3
(5.31)
dv serbest uzayda μ = μ0 olduğundan
G '
G
μ
J(x )
A (x) =
dv'
∫
3
v
4π x − x '
(5.32)
G
G
μ J(x ' )x(x − x ' ) '
B(x) =
dv
4π ∫v
'3
x−x
(5.33)
46
G
ince akım flamanı veya teliçin J ⋅ dv' → I ⋅ dl' ise
(5.34)
G
μ I
dl'
A (x) = 0 v∫
4π c x − x '
G
μ0 I dl' x(x − x ' )
B(x) =
4π v∫ c x − x ' 3
(5.35)
C devre yolunu göstermektedir. Bu Biot-Savart kanunu olarak bilinir. Yüzey
G
akımları için, J ⋅ dv' → K ⋅ ds olup K (A/m) olarak yüzey akım yoğunluğudur. S
yüzeyi boyunca K akımı akarsa aşağıdaki sadeleşmiş eşitlikleri elde ederiz;
G
μ
K(x ' )ds'
A(x) = 0 v∫
4π s x − x ' '
(5.36)
G
μ
K(x ' )x(x − x ' )ds'
B(x) = 0 v∫
3
4π s
x − x'
(5.37)
Kuvvet ve tork çözümlemesi
Bu tür problemlerde dış manyetik alanda akım kaynağından üretilen Kuvvet ve Tork
hesaplanır. Q yüklü bir parçacık bir Bext dış alan boyunca hareket ettiğinde
oluşturduğu Lorentz kuvveti şöyle olur;
G
G
F = q(u × Bext )
(5.38)
47
Özel bir durum olarak tel uzunluğu l dış alana paralel ise lorentz kuvveti aşağıdaki
biçime sadeleşir.
F = I ⋅ l ⋅ Bext
(5.39)
Eğer biz kuvvet yoğunluğu f’i biliyorsak Tork’u elde edebiliriz;
G
T = I ∫ r × (dl × Bext )
tel
(5.40)
Maxwell stress tensor
Yukarıda bahsedilen Lorentz kuvvetine alternatif ve en yaygın olarak kullanılan
Maxwell-Stress tensor yöntemidir. Bu yaklaşımda kuvvet yoğunluğu eşitliği;
f=
1
∇ ⋅ T ile verilir. Burada T "Maxwell − stress tensor "dür.
μ
⎡ 2 1 2
⎤
Bx B y
B x Bz
⎢(Bx − 2 B )
⎥
⎢
⎥
2
2 1
⎢
⎥
(B y − B )
B y Bz
[ T ] = ⎢ B y Bx
⎥
2
⎢
1 2 ⎥
⎢ Bz B x
Bz B y
(B2z − B ) ⎥
⎢⎣
⎥⎦
2
F=
1
2μ0
v∫ Bn ⋅ ds
2
s
(5.41)
(5.42)
48
Enerji
Manyetostatik bir alan enerji içerir ve bu enerjinin değeri şu şekilde elde edilir [5].
⎡A G
⎤
Wm = ∫ ⎢ ∫ J ⋅ dA ⎥dv
⎥⎦
v⎢
⎣0
(5.43)
⎡B G
⎤
Wm = ∫ ⎢ ∫ H ⋅ dB⎥dv
⎥⎦
v⎢
⎣0
(5.44)
Wm =
1 G G
A ⋅ J ⋅ dv
2 ∫v
(5.45)
Wm =
1 G G
B ⋅ H ⋅ dv
2 ∫v
(5.46)
İndüktans
İndüktans değeri;
L=
G G
1 G G
A
⋅
J
⋅
dv
=
∫
∫ B ⋅ H ⋅ dv doğrusal sistem
I2 v
I2 v
1
(5.47)
L = Li + Le
Li =
1
I2
G G
B
∫ ⋅ H ⋅ dv iletken içinde
vf
(5.48)
49
Le =
1
I
2
G G
∫ B ⋅ H ⋅ dv
iletken dışında
(5.49)
ve
Eşitlik 5.47, 5.48 ve 5.49 ile ifade edilir.
5.2.6. Akım modeli
Akım modeli sürekli mıknatıs çözümlemelerinde kullanılır. Bu modelde mıknatıs
eşdeğer akım dağılımına indirgenir. Bu daha sonra manyetostatik alan eşitlikleri
içerisine kaynak terimleri olarak girer ve alan sürekli akım için standart yöntemler
kullanılarak elde edilir.
G
G
G
μ 0 J m (x ' ) ' μ 0 J m (x ' ) '
A (x) =
dv +
ds
4π ∫v x − x '
4π v∫s x − x '
(5.50)
'
G
G
μ0 G
(x − x ' ) '
' (x − x ) ' μ 0
'
B(x) =
Jm (x )
dv +
ds
∫ Jm (x ) ×
4π ∫v
4
π
'3
'3
s
x−x
x−x
(5.51)
Bu eşitliklerde S mıknatıs yüzeyi, Jm ile jm eşdeğer hacim ve yüzey akım
yoğunlukları olup bu akımlar aşağıdaki gibi ifade edilirler.
G
Jm = ∇ × M
(A / m 2 ) hacim akım yoğunluğu
(5.52)
jm = ∇ × M (A / m) yüzey akım yoğunluğu
(5.53)
Akım modeli sürekli mıknatıslarda kuvvet ve tork hesaplamak için kullanışlıdır.
Kuvvet ve tork dış alanda akımların dağılımında kuvvet için temel ilişkiler
kullanılarak elde edilir.
50
G
G
G
F = ∫ Jm × Bext dv + v∫ jm × Bext ds
(5.54)
G
G
G
T = ∫ r × (Jm × Bext )dv + v∫ r × ( jm × Bext )ds
(5.55)
v
s
v
s
5.2.7. Yük modeli
Yük modeli sürekli mıknatısları çözümlemek için kullanılan diğer bir kullanışlı
yöntemdir. Bu modelde mıknatıs eşdeğer manyetik yük dağılımına indirgenir. Yük
dağılımı manyetostatik alan eşitliklerinde kaynak terim olarak kullanılır ve alanlar
standart yöntemler kullanılarak elde edilir.
ϕm (x) = −
1 ∇M(x ' )
1
M(x ' )n
dv
+
ds
4π ∫v x − x '
4π v∫ s x − x '
ρm = −∇ × M
(A / m 2 ) hacim yük yoğunluğu
σm = M × n (A / m) yüzey yük yoğunluğu
(5.56)
(5.57)
(5.58)
Sırasıyla kuvvet ve tork ise;
G
G
F = ∫ ρm × Bext dv + v∫ σm × Bext ds
(5.59)
G
G
T = ∫ ρm × (r × Bext )dv + v∫ σm × (r × Bext )ds
(5.60)
v
v
s
s
51
5.2.8. Sonlu farklar yöntemi
Sonlu farklar yönteminde kısmi türevli fark eşitliklerini, fark eşitlikler haline
getirebilmek için taylor serisine açılır. Buradaki üç ve daha yüksek dereceli türevler
göz ardı edilir. Bu yok saymalar kesme hatası denen hatayı oluştururlar. Sonlu
farklar yöntemini eğrisel sınırlara uydurmak zordur [5].
5.2.9. Sınır elemanlar yöntemi
Sonlu elemanlar ve sonlu farklar yöntemlerine göre daha az sayıda denkleme ve giriş
verisine gereksinim duyulur. Sistem matrisi seyrek değildir ve simetrik özelliği
yoktur. Denklem sistemini elde etmek için gerekli süre diğerlerine göre daha fazladır.
5.2.10. Yük benzetim yöntemi
Açık sınırlı alan problemlerine kolaylıkla uygulanabilir ve özellikle elektrostatik alan
problemlerinin çözümünde önemli üstünlüklere sahiptir. Sadece tek tip yalıtkandan
oluşan düzgün dağılımlı üç boyutlu alan problemlerine uygulanması zor değildir.
Çok tabakalı sistemlerin Sonlu elemanlar ve Sonlu farklar yöntemi ile basitçe
çözümleri yapılabilmektedir ama Yük benzetim yöntemi ile iki veya daha fazla
yalıtkandan oluşan sistemlerin alan hesabı daha zor yapılabilmektedir.
5.2.11. Sonlu elemanlar yöntemi
Sonlu Elemanlar Çözümlemeleri (Finite Element Analysis – FEA) günümüzde
elektromanyetik alan problemleri için kullanılmakta olan en popüler sayısal
yöntemdir. Çünkü birinci olarak, FEA çok geniş uygulama alanları için güçlü bir
yöntemdir. İkincisi, kullanıcıların kendi özel uygulamaları için ayrı bir algoritma
yazmalarına gerek bırakmayan çok sayıda ticari paket yazılımları bulmak olanaklıdır.
52
Sonlu eleman yöntemi aşağıdaki adımları gerektirir.
1.
Çözüm bölgesini elemen olarak adlandırılan alt bölümlere ayırmak ve her
elemanı tanımlayan düğümler işaretlemek.
2.
Her elemanda alan çözümü için genellikle polinom biçiminde olan yaklaşım
fonksiyonu seçmek.
3.
Her elemanda düğüm değerlerinin fonksiyonu olarak çözümü ve elemandaki
uzaysal değişkenleri ifade etmek.
4.
Alan denklemi için enerji fonksiyoneli tanımlamak ve bu fonksiyonu her eleman
için geliştirmek. Bu her elemanda onun düğüm değerleri terimleri olarak enerji
için tanımlanır.
5.
İç elemanlardaki enerjilerin toplamı olarak küresel enerji ifadesini kurmak. Bu
ifade önemsiz ve önceden tanımlanan düğüm değerlerinin elenmesiyle
bilinmeyen düğüm değerlerini azaltır.
6.
Bilinmeyen düğüm değerlerine uygun olarak küresel enerji ifadesi minimize
edilir.
7.
Düğüm değerlerini elde etmek için 6. adımdaki denklem sistemlerinin çözümü.
8.
Üçüncü adımdaki ifadenin kullanılarak düğüm değerlerinden istenilen çözümler
için yeniden kurulması.
53
Sayısal yöntemler, yüksek hızlı bilgisayarların gelişmesi ve yardımcı cihazların
kullanımının artmasıyla çok cazip bir hale gelmiştir. Böylece alan problemlerinin
incelenmesinde önemli adımlar atılmıştır. Ancak poisson ve laplace tiplerinde kısmi
türevli diferansiyel eşitliklerin çözümünde birçok zorluklar bulunmaktadır.
∂ 2φ
∂x 2
∂ 2φ
∂x 2
+
+
∂ 2φ
∂y 2
∂ 2φ
∂y 2
= f (x, y) Poisson eşitliği
(5.61)
=0
(5.62)
Laplace eşitliği
Özellikle iki veya üç boyutlu karmaşık alanların, farklı dielektrik sabitli ve iletken
malzemelerin matematiksel modellerini oluşturan eşitliklerin çözümü daha da
karmaşık olmaktadır. Genellikle problemlere ilişkin ortaya çıkan kısmi türevli
eşitliklerin analitik çözümü, çok basit durumların dışında, zor, zaman alıcı veya
olanaksız olmaktadır. Bu gibi durumlarda sayısal yöntemlerle çalışmak kaçınılmaz
bir durum olmaktadır.
Sonlu elemanlar yönteminde, deneme fonksiyonu aramada kullanılan dört alt yöntem
şunlardır.
1- Rayleigh- Ritz yöntemi
2- Galerkin yöntemi
3- En küçük kareler yöntemi
4- Ağırlık artıkları yöntemi
Bu yöntemlerden en yaygın olarak kullanılanı, Reigleih-Ritz ve Galerkin
yöntemleridir.
54
Rayleigh- Ritz yöntemi
Verilen sınır koşulları altında temel diferansiyel denklemi minimum yapan, sınır
değer problemlerin işlevsel olarak adlandırılan varyasyonel bir yöntemdir.
−∇ 2φ = f
(5.63)
L = −∇ 2
F = Lφ, φ − 2 φ, f
(5.64)
⎡⎛ ∂φ ⎞2 ⎛ ∂φ ⎞ 2
⎤
F = ∫ ∫ ⎢⎜ ⎟ + ⎜ ⎟ − 2φf ⎥ dxdy
⎢⎣⎝ ∂x ⎠ ⎝ ∂y ⎠
⎥⎦
Bu fonksiyonel Ф(x,y) deneme fonksiyonu ile yaklaşık olarak ifade edilir.
n
Φ = ∑ a jΨ j
(5.65)
j=1
Bu ifadelerde aj bilinmeyen katsayıları öyle belirlemeli ki fonksiyonel en küçük
olsun. Yönteme göre deneme fonksiyonu, koordinat fonksiyonları denilen
fonksiyonların toplamı şeklinde ifade edilecek olursa Ф, F de yerine konularak,
fonksiyonel Ψ(j) ve aj ler cinsinden yazılmış olur. Burada kullanılan aj bilinmeyen
katsayılardır. Bu katsayılar, F minimum olacak şekilde
belirlenir.
∂f
= 0 İfadesinden
∂a j
55
Bu işlemle bir doğrusal cebirsel denklem takımı elde edilir. Bu eşitliklerin çözümü
ile aj’ler belirlenerek Ф deneme fonksiyonu bulunur. Böylece elde edilen Ф,
fonksiyoneli en küçük yaparken ilgili poisson denklemini gerçeklemiş olur [5].
2
2
⎡⎛
⎤
∂Ψ j ⎞ ⎛
∂Ψ j ⎞
⎢
F = ∫ ∫ ⎜∑aj
⎟ + ⎜∑aj
⎟ − 2∑ a jΨ jf ⎥ dxdy
∂x ⎠ ⎝
∂y ⎠
⎢⎝
⎥
⎣
⎦
(5.66)
Bu ifade aj inci kat sayıya göre yeniden düzenlenecek olursa;
F = ai2
2
2
⎡⎛
n
∂Ψj ⎞ ⎛
∂Ψj ⎞ ⎤
⎛ ∂Ψ ∂Ψj ∂Ψ ∂Ψj ⎞
⎢
⎥
a
a
dxdy
2
+
−
∑aiaj ∫∫⎜ ∂xi ∂x + ∂yi ∂y ⎟dxdy − 2 (5.67)
∫∫ ⎢⎜⎝ ∑ j ∂x ⎟⎠ ⎜⎝∑ j ∂y ⎟⎠ ⎥
⎝
⎠
j=1
⎣
⎦
a i ∫ ∫ Ψ i fdxdy + a i ’ yi içermeyen terimler bu ifade kısaltılarak yazılırsa
F = k ija i2 + 2Kija i − 2a i bi + a i ’ yi içermeyen terimler F’ in en az olması için
∂f
= 0 olmalıdır.
∂a j
Buradan,
∂f
= 2Aij.a i + 2Aij − 2bi = 0
∂a j
(5.68)
Aij.a i + Aij = bi
(5.69)
56
Ve genel olarak ifade edilecek olursa,
∑ j = Aij.a i = bi
i = 1, 2,3,............, n
(5.70)
elde edilir. Buradaki katsayılar açık olarak yazılırsa,
⎛ ∂Ψ i ∂Ψ j ∂Ψ i ∂Ψ j ⎞
+
Aij = ∫ ∫ ⎜
⎟dxdy
∂
x
∂
x
∂
y
∂
y
⎝
⎠
(5.71)
bij = ∫ ∫ Ψ i ⋅ f ⋅ dx ⋅ dy şeklini alır.
Sonlu elemanlar ve Ragleigh-Ritz yöntemi
Sonlu elemanlar yönteminin esası, karmaşık sınır koşulları nedeniyle tüm çözüm
bölgesi için bir potansiyel fonksiyonu bulmanın mümkün olmadığı durumlarda,
çözümü sonlu küçük elemanlar içinde aranmasına dayanır. Çözüm için elemanları
geometrik yapısında kalmak koşulu ile tüm çözüm bölgesi aynı geometrik
elemanlara bölünür. Bu geometrik elemanlar üçgen, dörtgen ve benzeri şekiller
olabilir. Düzensiz şekillerde ve gelişi güzel bölümlendirmelerde üçgen elemanlar
kolaylık ve sınır yüzeylere kolayca uyum sağlar. Genel olarak n’ inci dereceden çok
terimli biçimde iki boyutlu potansiyel yaklaşım işlevi;
φ(x, y) = α 0 + α1x + α 2 y ’dir
(5.72)
Şekil 5.1’deki tek üçgen için deneme fonksiyonu olarak birinci derecedeki bir
polinomla ifade edilir. Bu deneme fonksiyonunda Ф, x ve y’ ye göre doğrusal bir
şekilde değişmektedir. Eğer üçgenin köşelerinde potansiyeller Фi , Фj , Фm ise,
deneme fonksiyonu bu köşe noktalarında, bu değerleri sağlamak zorundadır. Bu
nedenle aşağıdaki ifadeler yazılabilir.
57
α 0 + α1x1 + α 2 yi = φi
α 0 + α1x j + α 2 y j = φ j
(5.73)
α 0 + α1x m + α 2 y m = φm
Şekil 5.1. Bir üçgen eleman
Şekil 5.1’deki üçgenin alanı, köşe koordinatları cinsinden şu şekildedir.
1
Δ=1
xi
xj
yi
yj
1 xm
ym
(5.74)
Denklem 5.74 ifadelerinin α0 , α1 ve α2 değerleri bulunarak deneme fonksiyonunda
yerine yazmak üzere aşağıdaki kısaltmalar yapılırsa,
ai = xj ym – xm yi, bi = yj – ym, ci = xm – xj
58
aj = xm yi – xi ym, bj = ym – yi, cj = xi - xm
am = xi yj – xj yi, bm = yi – yj, cm = xj – xi
Ni =(ai + bix + ciy ) /2Δ
Nj =(aj + bjx + cjy ) /2Δ
Nm =(am + bmx + cmy ) /2Δ
elde edilir.
Bu yeni tanımlamalar deneme fonksiyonundaki yerlerine yazılacak olursa;
Ф(x,y)= Ni(x,y) Фi+Nj (x,y) Фj+Nm(x,y) Фm
(5.75)
şeklinde yazılır.
Üçgen elemanların birleştirilmesi
Herhangi bir üçgen eleman için elemanın enerjisi hesaplanır. Tüm bölge içindeki
toplam enerji, eleman enerjilerinin toplamına eşittir. Çözümü aranan potansiyel
işlevinin tüm bölge içinde, elemanlar arasındaki sınırlarda sürekli olması gerekir. Bir
üçgen elemanın içinde ve kenarlarında potansiyel doğrusal olarak değişir.
59
Şekil 5.2. İki üçgen eleman
⎡⎛ s1
⎢⎜ 11
⎢⎜ s1
⎢⎜ 21
⎢⎜⎜ s1
⎢⎣⎝ 31
⎡⎛ s 2
⎢⎜ 11
⎢⎜ s 2
⎢⎜ 21
⎢⎜⎜ s 2
⎢⎣⎝ 31
s112
s122
s1
32
s 212
s 222
s2
32
s113 ⎞ ⎤ φ
⎟ ⎥ ⎡ 1 ⎤ ⎡0⎤
1 ⎟⎥ ⎢ ⎥ ⎢ ⎥
s 23 ⎢φ2 ⎥ = ⎢ 0 ⎥
⎟⎥
⎥ ⎢ ⎥
1 ⎟⎥ ⎢
s 33 ⎟ ⎥ ⎣ φ3 ⎦ ⎣ 0 ⎦
⎠⎦
(5.76)
s 213 ⎞ ⎤ φ
⎟ ⎥ ⎡ 1 ⎤ ⎡0⎤
2 ⎟⎥ ⎢ ⎥ ⎢ ⎥
s 23 ⎢φ2 ⎥ = ⎢ 0 ⎥
⎟⎥
⎥ ⎢ ⎥
2 ⎟⎥ ⎢
s 33 ⎟ ⎥ ⎣ φ3 ⎦ ⎣ 0 ⎦
⎠⎦
(5.77)
5.76 ve 5.77 matrisleri toplanarak 5.78 matrisi elde edilir.
⎡⎛ s1
s 211 s 212 s113
11
⎢⎜
⎢⎜ s 2
s 222
⎢⎜ 21
⎢⎜ s1 + s 2 s 2 s1 +
31 32 33
⎢⎜ 31
⎢⎜ s1
0
⎣⎢⎝ 41
s 213
s 223
s 233
s143
s114 ⎞ ⎤
⎟ ⎥ ⎡ φ1 ⎤ ⎡ 0 ⎤
⎟
0 ⎥ ⎢ φ2 ⎥ ⎢ 0 ⎥
⎟⎥ ⎢ ⎥ = ⎢ ⎥
1 ⎟ ⎥ ⎢ φ ⎥ ⎢0⎥
3
s 34
⎟⎥ ⎢ ⎥ ⎢ ⎥
φ
0
s144 ⎟⎠ ⎥⎥ ⎣ 4 ⎦ ⎣ ⎦
⎦
(5.78)
İkiden fazla eleman benzer şekilde birleştirilir. Şekil 5.3’de 4 elemandan oluşan
sistemin katsayı matrisi eşitlik 5.79 dadır.
60
Şekil 5.3. Dört üçgen eleman
⎡ s(1+ 2)
⎢ 11
⎢ s(1)
21
⎢
⎢ (1+ 2)
⎢ s 31
⎢
(2)
⎢ s 41
⎢
0
⎢
⎢
⎢
0
⎣
s(1)
s(1+ 2)
s(1)
0
0
s(1+ 4)
s(1+ 4)
0
0
s111
s(1+ 4)
s(1+ 2+3+ 4)
s(2+3)
s(3)
s(4)
0
(2+3)
(2+3)
(3)
0
12
22
32
13
14
13
33
s
43
34
s
44
35
s
45
36
0
s(3)
s(3)
s(3)
0
s(4)
s(4)
0
0
s(4)
62
53
63
54
55
66
⎤
⎥
⎥ ⎡ φ1 ⎤ ⎡ 0 ⎤
⎥ ⎢φ ⎥ ⎢0⎥
⎥⎢ 2⎥ ⎢ ⎥
⎥ ⎢ φ3 ⎥ ⎢ 0 ⎥
⎥ ⎢φ ⎥ = ⎢0⎥
⎥⎢ 4⎥ ⎢ ⎥
⎥ ⎢ φ5 ⎥ ⎢ 0 ⎥
⎥⎢ ⎥ ⎢ ⎥
⎥ ⎣⎢ φ6 ⎦⎥ ⎣ 0 ⎦
⎥
⎦
(5.79)
S terimlerinin üst indisleri eleman numaralarını, alt indisler de düğüm numaralarını
göstermektedir.
Komşuluk ilişkisi olmayan düğümlerin oluşturduğu s katsayısı (0) sıfır olmaktadır.
İki üçgenden fazla elemandan oluşan çözüm bölgesinden elde edilen denklem
takımına dikkat edildiğinde matrisin bant yapıda olduğu görülür.
Matrisin bant genişliğini, bir üçgen elemanın iki düğüm numarası arasındaki fark
sayısının en büyüğü olan sayı belirler. Bant genişliğini mümkün olduğu kadar küçük
61
tutabilmek için üçgen elemanların düğümleri numaralandırılırken komşu iki düğüm
numarası arasındaki farkın mümkün olduğu kadar küçük tutulması gerekir [5].
61
6. EKSENEL AKILI KALICI MIKNATISLI MAKİNALARIN TASARIMI
Çalışmanın ilk hedefi; yüzey yerleştirmeli eksenel akılı kalıcı mıknatıslı makinalar
tasarlayarak uygun bir analitik tasarım yöntemi geliştirmektir. Bu konuda; geliştirilen
tasarım metodu açıklanmış ve yüzey yerleştirmeli eksenel akılı kalıcı mıknatıslı
makinanın performans hesabını belirleyen ana faktörler tartışılmıştır.
6.1. Giriş
Eksenel akılı PM makineleri modelleme; hesaplamaların hızı ve doğruluğuna bağlı
olan tutarsız gereksinimler ile belirlenir. Modellemeye bakış açısından, eksenel akılı
makine temelde 3 boyutlu bir geometriye sahiptir. Bu yüzden, ortalama makine
yarıçapında gerçekleştirilecek olan hem analitik tasarım metodu hem de 2D sonlu
elemanlar (FEA) analizi kullanmak genellikle yeterli bir doğru hesaplama sonucu
vermez. 3D FEA ile makinenin gerçek 3D yapısını dikkate almak mümkündür, fakat
hesaplamaları
gerçekleştirmek;
özellikle
hedef
makinanın
ilk
tasarımını
gerçekleştirmek ise çok fazla zaman alan işlemdir. Eksenel akılı yüzey yerleştirmeli
PM makinelerin modelleme sorusunu çözmek için, bu çalışmada analitik bir tasarım
metodu geliştirilmiş ve amaçlanmıştır. Tasarım metodunun temel fikri; öncelikle
eksenel akılı makineyi yeterli miktarda bağımsız hesaplama düzlemine ayırmak ve
ardından her düzlem üzerinde gerekli hesaplamaları yapmaktır ve sonunda her
tasarım düzleminden elde edilen hesaplama sonuçlarından tüm makine performansını
elde etmektir. Bu tarz bir tasarım metodu; quasi-3D hesaplama adını almaktadır. Bu
tez için geliştirilmiş olan uygun analitik tasarım aracı; lineer olmayan relüktans ağı
Rasmussen ve ark. ve Gieras tarafından verilen örnekte gösterilen analitik tasarım
metotları yardımı ile quasi-3D hesaplama yöntemini kullanmaktadır [25,26].
Geliştirilen
hesaplama
modelinin
makinenin
performansı
üzerinde
etki
oluşturabilecek 3D manyetik akı davranışını göz önünde bulundurmayacağına dikkat
ediniz. Modelin bu eksikliği; laminasyonların yönlendirilmesinden dolayı çoğu
tasarım durumunda önemsiz olarak göz önünde bulundurulabilir, fakat demir
62
parçaları doyuma ulaşacak şekilde tasarlanırsa, 3D manyetik akı akışının sebep
olduğu etkilerin de incelenmesi gerekmektedir.
Özellikle eksenel akılı makinelerle kısmi olarak uğraşan yeni ders kitaplarına göre,
eksenel akılı PM makinenin tasarımı; makinenin ortalama yarıçapını bir tasarım
düzlemi olacak şekilde kullanarak elde edilmektedir. Mıknatıs genişliği-kutup
uzunluğu oranı (bağıl mıknatıs genişliği); stator yarıçapının bir fonksiyonu olan
kutup uzunluğuna bağlı olarak sabit ise bu yaklaşım; motor performansını tahmin
etmek için yeterli derecede doğrudur. Bağıl mıknatıs genişliği motor yarıçapına göre
değişirse, yüksüz durumdaki hava aralığı akı yoğunluğu dalga formu; indüklenen zıt
EMK temel bileşeninin farzedilen değerden farklı olmasına sebep olarak değişir.
Stator sargısı tasarlanırken, istenen zıt EMK değerini elde edebilmek için bu değerin
dikkate alınması gerekmektedir.
Düşük hızlı kalıcı mıknatıslı makineler için, bakır kayıpları genellikle kayıp
bileşeninin çoğunu oluştururlar ve iyi bir verim elde edebilmek ve anma hızı
şartlarından önce, invertörün alan zayıflama bölgesinde çalışmasını engellemek için
istenen sipir sayısını minimize etmek önemlidir. Demir kayıplarını göz önünde
bulundururken, tasarım düzlemi olarak ortalama yarıçapı kullanmak yanıltıcı olabilir.
Bu durum; bir dişteki akı yoğunluğunun makine statorunun iç yarıçapında ve
sırasıyla dış yarıçapta stator boyunduruğunda genellikle maksimum 36 değerine
ulaşmasından dolayı meydana gelir. Bu; Şekil 6.1’de gösterildiği gibi kalıcı
mıknatısın şekline bağlıdır.
63
Şekil 6.1. Stator boyunduruğunda ve stator dişlerinde kalıcı mıknatıs şekli ile elde
edilen akı yoğunluğu seviyesi arasındaki ilişki. (a) bağıl mıknatıs genişliği;
stator içi yarıçapına doğru azalmaktadır. Bu durumda, dış yarıçapta
boyundurukta doyma oluşabilir. (b) bağıl mıknatıs genişliği; statorun dış
yarıçapına doğrı azalmaktadır. Bu durumda, iç yarıçapta stator dişlerinde
doyma oluşabilir [1].
Demir kayıpları; akı yoğunluğunun bir fonksiyonu olarak doğrusal olmadığı için, her
tasarım düzlemi için demir kayıplarını ayrıca hesaplayan quasi-3D hesaplama
yönteminin kullanılması tavsiye edilmektedir. Akı yoğunluğu; makinenin iç ve dış
yarıçaplarında ciddi derecede birbirinden farklı ise, akı parçaları; manyetik devrede
diagonal olarak da akar. Bu durum; akı tamamen laminasyon yönünde akmadığından
laminasyonlarda ekstra eddy akım kayıplarına neden olur. Demir kayıpları
üzerindeki akı davranışının boyutu; gelecekte yapılacak çalışmalar için merak
uyandırabilir fakat bu çalışmada göz önünde bulundurulmamıştır.
64
6.2. Analitik quasi-3D modelleme
Quasi-3D modelleme ile ilgili olarak, eksenel akılı PM makinelerin farklı radyal
uzunluğu
olan
birkaç
eksenel
akılı
makinelerden
oluştuğu
göz
önünde
bulundurulabilir. Eksenel akılı bir makinenin tam performansı; bireysel makinelerin
performansları toplanarak ve makinenin derinliği yönündeki mümkün akı akışı ihmal
edilerek elde edilebilir. Bu yaklaşım; makine yarıçapı yönünde farklı mıknatıs
şekillerinin göz önünde bulundurulmasına ve dişlerin genişliğinin değiştirilmesine
izin verir. Quasi-3D hesaplasında kullanılacak eksenel akılı bir makinenin 3D
geometrisini 2D modele dönüştürme metodu Şekil 6.2’de gösterilmiştir. Şekil 6.3’te
quasi-3D modelleme ana geometrik parametreleri gösterilmektedir.
Adım 1: Hesaplama düzlemlerinin seçimi. Bu durumda; eksenel akılı makinenin
ortalama yarıçapında dr kalınlığı olan sadece bir hesaplama düzlemi seçilir.
Adım 2: Seçilen hesaplama düzlemi; derinliği dr olan 2D bir model olarak gösterilir.
Şekil 6.2. Eksenel akılı bir makinenin 3D geometrisini quasi-3D hesaplamada
kullanılabilecek 2D bir geometriye dönüştürme metodu [1].
65
(a)
(b)
Şekil 6.3. wPM mıknatıs genişliği, τ p kutup uzunluğu, lPM sabit kalınlık, ly stator
boyunduruğu kalınlığı ve g fiziksel hava aralığı uzunluğu tanımlamaları.
(b)’de sırasıyla; rin makine statorunun iç yarıçapı, rout dış yarıçap ve ls;
stator yığını uzunluğudur.
3D-hesaplama için, makinenin dış çapından başlanarak i kısmi hesaplama
düzleminin Dave ortalama çapı; aşağıdaki eşitlik ile verilmektedir:
Dave = Dout − j
ls
N
(6.1)
Burada;
Dout: Statorun dış yarıçapı,
N: Bir hesaplamada kullanılan hesaplama düzlemlerinin sayısı,
ls: Stator yığınının uzunluğu (m).
j (6.1) parametresi şu şekilde tanımlanır:
j = 2i-1.
(6.2)
66
(6.2)’deki i indeksinin 1’den N’ye gittiğini unutmamak gerekir. Ls stator yığınının
uzunluğu şu şekilde tanımlanır:
ls =
Dout − Din
2
(6.3)
Burada;
Din: Eksenel akılı makine statorunun iç çapıdır.
Her hesaplam düzlemi için τ p kutup uzunluğu şu eşitlikle verilmektedir:
τp,i =
πDave
2p
(6.4)
Burada;
p kutup parçası sayısıdır.
Genellikle, bağıl mıknatıs genişliği α p ; makine yarıçapı boyunca değişebilir. Şu
şekilde tanımlanmaktadır;
α p,i =
w PM,i
τp,i
(6.5)
Burada;
wPM,i ; Şekil 6.3’a göre i hesaplama düzleminde mıknatıs genişliğidir.
Denklemlere bağlı olarak eşitlik 6.1 ve eşitlik 6.5, makineyi belirli miktarda
hesaplama düzlemine bölmek mümküdür. Hesaplama için ihtiyaç duyulan hesaplama
düzlemlerinin sayısı, hesaplama amacına bağlıdır. En basit durumda, mıknatısın
67
bağıl genişliği sabit ve stator eğik değil ise indüklenen gerilimlerin ya da vuruntu
torkunun hesaplanması için sadece bir hesaplama düzlemine ihtiyaç vardır. Fakat,
demir kayıplarının hesaplanması için, demir kayıplarının doğrusal olmayan
davranışından dolayı bir hesaplama düzlemi yeterli değildir. Genellikle, gerek
duyulan hesaplama düzlemlerinin miktarı; duruma bağlıdır ve ilgili duruma göre
tanımlanmalıdır.
Faz dirençleri, indüktansları ve yük açısı gibi motor parametrelerinin hesaplanması;
klasik elektrik makineleri tasarım metotları kullanılarak elde edilebilir. Bu hesaplama
metotları; Gieras tarafından örnek olarak verilmektedir. Eksenel akılı makinenin
geometrisi; doğasından dolayı bir 3D problemi olsa bile, göz önünde bulundurulan
parametrelerin makine yarıçapına göre doğrusal olarak değişmesinden veya tamamen
yarıçaptan bağımsız olmasından dolayı makine parametrelerinin hesaplanması;
tasarım düzlemi olarak ortalama yarıçap rave’nin kullanımına bağlıdır [20,26].
6.2.1. Manyetik eşdeğer devre
Hesaplama modelinde, motorun farklı parçalarındaki akı yoğunlukları doğrusal
olmayan relüktans ağına bağlı olarak bulunur. Bu tarz ağların elektrik makinelerinin
doğru analizi için uygun olduğu kanıtlanmıştır [25,27]. Şekil 6.4’de kutup ve faz
başına oluk sayısı eşit olan eksenel akılı makine yapısının modellenmesi için
kullanılan doğrusal relüktans ağı parçasını göstermektedir. Tüm relüktans modeli;
simetri şartları yerine getirildiği için bir kutup parçasından meydana gelmektedir.
68
Şekil 6.4. Bir kutup üzerindeki relüktans ağının gösterilmesi. ℜ y ; stator
boyunduruğunun relüktansı, ℜt ; diş relüktansı, ℜ s ; açık oluğun
relüktansı, ℜ g ; hava aralığı ve fiziksel hava aralığı relüktansı, kalıcı
mıknatıs etkileri ve rotor çeliği etkilerinin toplamıdır. FPM; kalıcı
mıknatıstan dolayı ve F1; stator akımlarından dolayı oluşan mmf’dir.
Bu çalışmada, EAKM makinelerin tasarımını elde etmek amacıyla amaçlanan
analitik tasarım aracı geliştirilmiştir. Bu yüzden, relüktans ağı oldukça kaba kalır ve
doğruluk anlamında FE-Metodu ile uyumlu değildir. Fakat dişlerde, stator
boyunduruğunda ve rotor diskindeki maksimum akı yoğunluk seviyelerini
hesaplamak oldukça doğrudur. Relüktans ağı; her hesaplama düzlemi için yüklü ve
yüksüz durumlar altında çözülür. Hesaplanan relüktanslara bağlı olarak, etkin hava
aralığına demir doyum etkisi eklenir. Dişlerde ve stator boyunduruğunda elde edilen
maksimum akı yoğunlukları; demir kayıplarının hesaplanması için kullanılır.
Doğrusal olmayan relüktans ağı, aşağıdaki eşitliğe göre tekrarlanarak çözülür:
Φ = ℜ−1F
Burada;
(6.6)
69
Φ ; Manyetik akı matrisi,
ℜ ; Relüktans matrisi,
F; Kalıcı mıknatıs ve stator faz akımlarından dolayı oluşan MMF kaynaklarını
içeren kaynak matrisidir.
Relüktans matrisi için, kısmi relüktans olan ℜi ; şu şekilde hesaplanır;
ℜi =
li
μ0μ rSi
(6.7)
Burada;
li ; Bir relüktans elemanı ile birlikte modellenen makinenin kısmi parçasının
uzunluğu,
μ r ; Relüktans elemanı materyalinin bağıl geçirgenliği,
Si ; Bir relüktans elemanı ile birlikte modellenen makinenin kısmi parçasının kesit
alanıdır.
Demir parçalarının bağıl geçirgenliği μ r ; akı yoğunluğunun bir fonksiyonudur.
Sonuç olarak, eşitlik 6.6’ nın doğru değeri; tekrarlanarak (iterasyon ile) bulunmalıdır.
Stator laminasyonunun demir relüktansları; B-H eğrileri kullanılarak modellenir ve
rotor materyali için inşaat çeliği kullanılır.
Her stator faz akımı tarafından üretilen mmf aşağıdaki gibi hesaplanır:
FI,ph = Ns I
Burada;
Ns ; Bir oluktaki spir sayısı,
(6.8)
70
I ; Bir turluk bobinden geçen akımdır.
Kalıcı mıknatıs tarafından üretilen mmf FPM aşağıdaki gibi hesaplanır:
FPM =
Br lPM
μ0μ r,PM
(6.9)
Burada;
l PM ; Şekil 6.3’te tanımlanan kalıcı mıknatısın kalınlığıdır.
Eşitlik 6.6 çözümü; her relüktans elemanı içersinden geçen manyetik akı değerlerini
vermektedir. Bilinen manyetik akı değeri ve kısmi relüktans elemanının kesit alanına
bağlı olarak, bir elemandaki akım yoğunluğunu aşağıdaki gibi hesaplamak
mümkündür:
Bi =
Φi
Si
(6.10)
6.10 eşitliği ile sağlanan akı yoğunluğu büyüklükleri; demir kayıplarını hesaplarken
kullanılmaktadır.
Stator laminasyonunun ve rotor materyalinin bağıl geçirgenliği sonsuz değil ise,
stator ve rotor demiri üzerindeki akı yolunda manyetik bir gerilim düşümü elde
edilir. Bu durum; hava aralığındaki etkin akı yoğunluk seviyesini düşürür ve makine
tasarlarken dikkate alınmalıdır. Hesaplama modelinde demir doyumunu dikkate
almanın mümkün bir yolu; doyum faktörü ksat adı verilen bir düzletme faktörü
kullanmaktır [26]. Bu durumda, etkin hava aralığı uzunluğu geff aşağıdaki gibi
hesaplanır:
g eff = k sat k c g = k sat g '
(6.11)
71
Burada;
ksat ; Doyma katsayısı,
kC ; Stator oluğunu dikkate alan Carter’s katsayısı,
g; Hava aralığının fiziksel uzunluğu.
Doyma faktörü; kutup başına manyetik gerilim düşümünün hava aralığı manyetik
gerilim düşümüne oranı olarak tanımlanmaktadır [26].
k sat =
Θagap + Θ t + 0.5(Θ y + Θrotor )
Θagap
(6.12)
Burada;
Θ agap ; Hava aralığındaki manyetik gerilim düşümü (hava aralığının uzunluğu; kalıcı
mıknatıs Lpm’nin kalınlığı ve hava aralığı g’nin uzunluğunu içermektedir).
Θt ; Stator dişleri boyunca meydana gelen manyetik gerilim düşümü,
Θ y ; Stator boyunduruğu boyunca meydana gelen manyetik gerilim düşümü,
Θ rotor ; Rotor nüvesi boyunca meydana gelen manyetik gerilim düşümü.
Hesaplama modeli için, doyum faktörünün değeri; stator üzerindeki manyetik gerilim
düşümü ve her hesaplama düzleminin rotor relüktansları ayrı ayrı hesaplanarak elde
edilir. Yarıçapa göre değişebilen doyum seviyesi; bundan sonra quasi-3D modelleme
içersinde dikkate alınabilir.
72
6.2.2. Kalıcı mıknatıs kaçak akılarının hesaplanması
Yüzey yerleştirmeli kalıcı mıknatıslı makine tasarımı için, kalıcı mıknatıs kaçak
akılarının faydalı manyetik akı üzerinde güçlü bir azatlım etkisine sebep olduğu
dikkate alınmalıdır. Kaçak akılardan dolayı oluşan kalıcı mıknatıs akısı
φPM ’yi
azalatmak için, analitik çözümde de belirtilen bir kaçak katsayısı kullanılabilir. Etkin
akı φeff aşağıdaki formül ile ifade edilir:
Φ eff = k σPM Φ PM
(6.13)
Burada;
kσPM Kalıcı mıknatıs akısı kaçak katsayısıdır.
Metodun sakıncası şudur; yüksek doğruluk talep ediliyorsa, her tasarım için doğru
kaçak katsayısını kσPM bulabilmek için 3D sonlu elemanlar analizine gerek vardır.
Analitik hesaplamalarda, Hwang, tarafından verilen ve Qu ve ark. tarafından
geliştirilen metot kullanılarak kaçak katsayısı kσPM ihmal edilebilir [28,29]. Analizde,
Qu’nun modeli kullanılarak mıknatıs kaçak faktörü hesaplanmış ve metot; karmaşık
mıknatıs yapılı eksenel akılı makineleri kapsayacak şekilde geliştirilmiştir. Eksenel
akılı yüzey yerleştirmeli kalıcı mıknatıslı makineler için etkin kaçak katsayısı
aşağıdaki gibi hesaplanabilir:
N
k σPM =
∑ k σPM,i
i =1
N
k σPM,add
Burada;
kσPM ,add ; Ek kaçak katsayısıdır.
(6.14)
73
Ek kaçak katsayısı k σPM,add ; kaçak akı modelinde gösterilmeyen ek kaçak akı
bileşenlerinin sebep olduğu etkin akının azaltılmasını kapsamaktadır. Bu bileşenler;
oluk açıklıkları ile oluklar içersinden mıknatıs kutbundan bitişik mıknatıs kutbuna
akan akılarda olduğu gibi statorun iç ve dış yarıçapında mıknatıs ile rotor arasında
oluşan kaçak akılardır.
Kalıcı mıknatıs kaçak faktörü k σPM iki kaçak bileşenini içermektedir: [29].
1. Şekil. 6.5 (a)’da gösterilen kalıcı mıknatıs zigzag kaçağı
2. Aşağıdaki bileşenlerden oluşan kalıcı mıknatıs hava aralığı kaçağı:
•
Şekil. 6.5 (b)’de gösterilen mıknatıs-rotor kaçağı
•
Şekil. 6.5 (c)’de gösterilen mıknatıs-mıknatıs kaçağı
Şekil 6.5. (a) Mıknatıslar stator demiri aracılığı ile kısa devre yapıldığında zigzag
kaçak akı yolları (b) Mıknatıs-rotor kaçak akısı. (c) Mıknatıs-mıknatıs
kaçak akısı
Her hesaplama düzleminin kalıcı mıknatıs hava aralığı kaçak katsayısı Qu ve ark.
larına göre hesaplanmaktadır.
74
k σPM,agap,i =
1
⎛
w PM,i ⎞
g'
1 + ⎜ μ r,PM
⎟⎟
⎜
+
l
w
2g
'
PM
PM,i
⎝
⎠
1
.
⎛
⎛
⎛
2lPM
4lPM
πg ' ⎞
πg '
⎜
ln ⎜ 1 +
ln ⎜1 +
+
⎟
⎜
⎜ πμ
w
lPM ⎠ πμ r,PM w PM,i ⎝ τp,i − w PM,i
⎝ r,PM PM,i ⎝
(6.15)
⎞⎞
⎟⎟
⎟⎟
⎠⎠
Burada;
g´ Carter katsayısı kC ile çarpılan hava aralığı fiziksel uzunluğu Zigzag kaçak faktörü
aşağıdaki gibi hesaplanır [29];
k σPM,zz,i
( τslot,i − ( τp,i − w PM,i ))
= 1−
2
2w PM,i τslot,i
(6.16)
Burada;
τ slot Oluk uzunluğudur.
Her hesaplama düzlemi için etkin kaçak faktörü şu eşitlik ile verilmektedir:
k σPM,i = k σPM,agap,i k σPM,zz,i
(6.17)
Zigzag kaçak; Şekil 6.5 (a)’da gösterildiği gibi mıknatıstan bitişik mıknatısa hava
aralığı ve diş ucu aracılığı ile akan kaçak akıyı temsil etmektedir. Zigzag kaçağın
bitişik iki mıknatıs arasındaki uzaklık bir oluk uzunluğundan daha küçük iken var
olduğu kabul edilir. Yüzey yerleştirmeli mıknatıslı makine için zigzag akı bileşeni
genellikle hava aralığı kaçak akısından daha büyüktür [29].
75
6.2.3. Hava aralığı akı yoğunluk dağılımı için analitik model
Bir faz sargısını boyutlandırmak için, hava aralığı akı yoğunluğu dağılımının temel
bileşeni gerekli bir parametredir. Hesaplama modeli için, hava aralığı akı yoğunluğu
dağılımının temel bileşeni; stator ve rotor demirinin sonsuz bağıl geçirgenliği
varsayılarak elde edilen hava aralığı akı yoğunluk dağılımının analitik ifadesine bağlı
olarak belirlenir. Radyal akılı makineler için, sadece kalıcı mıknatıs tarafından
üretilen hava aralığı akı yoğunluk dağılımının analitik ifadesi B (θ ) ; Zhu vd.
tarafından verilmiştir [30].
Lineer makineler olarak göz önünde bulundurulan
eksenel akılı makineler için, B(x) dağılımı olan Kartezyen koordinat sistemini
kullanmak daha uygundur. Bu ifade; Hanselman ya da Chung ’da verilmiştir [31,32].
İkinci yaklaşım; bundan sonra eksenel akılı kalıcı mıknatıslı makinalar için
kullanılmaktadır.
nπg '
⎛ nπx ⎞
⎡ α p,i ⎤ − τp,i
8Br
sin ⎢
e
cos ⎜
⎟
⎥
⎜ τp,i ⎟
∞
nπ
⎣ 2 ⎦
⎝
⎠
BPM,i (x) = − ∑
2n
g
'
2n
π
⎛ −
⎞ ⎛ − πlPM
⎞
n =1,2,3....
τ
τp,i
⎜
⎟
⎜
p,i
μ PM −e
+1 e
+ 1⎟
2nπg '
⎜
⎟
⎜
⎟
−
⎜
⎟⎜
⎟
τp,i
⎝
⎠
⎝
⎠
+ 1) +
(e
2n
l
π
PM
⎛ −
⎞
τp,i
⎜
μ0 e
− 1⎟
⎜
⎟
⎜
⎟
⎝
⎠
(6.18)
Burada;
μPM ; Kalıcı mıknatısın geçirgenliğidir.
~
Modelde, bağıl geçirgenlik fonksiyonu işleme konularak λ ( x) oluk açıklıklarının
BPM(x) dalga şekli üzerinde etkisi dikkate alınmıştır [33].
76
Bağıl geçirgenlik dağılımı; şekil 6.6(a)’da gösterilmeketedir. Oluk açıklıklarının
etkisini içeren hava aralığı akı yoğunluğu dağılımı Bagap(x) aşağıdaki eşitlik ile
verilmektedir:
∼
Bagap,i (x) = λ(x)BPM,i (x)
(6.19)
Kullanılan yaklaşım; oluk açıklığının yakınında diş ucunun altında akı yoğunluğunun
büyüklüğünü arttıran diş uçları yakınındaki akı yoğunluğunu göz önünde
bulundurmaz. Bu etki; Şekil 6.6(b)’de açıklanmıştır. Demir parçaları için sonsuz bir
geçirgenlik varsayılmıştır, böylece g değerinin yerine geff değeri konularak
hesaplama doğruluğu arttırılabilir, her hesaplama laminasyonu için kullanılan geff
değeri; (6.11)’e göre stator laminasyonu ve rotor demirinin sebep olduğu manyetik
gerilim düşümünü içermektedir. (6.18)’de g yerine geff yerleştirilerek hava aralığı
fiziksel uzunluğu artar ve böylece Bpm(x) büyüklüğünde bir düşme elde edilir.
(a)
(b)
Şekil. 6.6. Bağıl geçirgenlik ve hava aralığı akı yoğunluğu dağılımı, (a) Bağıl
geçirgenlik dağılımı. (b) Oluk açıklıklarının etkilerini içeren hava
aralığı akı yoğunluk dağılımı.
77
Sonuçta ortaya çıkan hava aralığı akısı yoğunluğunun temel bileşeni Bagap1 eşitlik
6.19’a ve aşağıdaki eşitliğe bağlı olarak değerlendirilir:
N
Bagap =
∑ Bagap,i
i =1
N
(6.20)
Burada;
Bˆ agap1,i ; Kalıcı mıknatıs tarafından üretilen hesaplama düzlemi i üzerindeki hava
aralığı akısı yoğunluğu temel bileşeninin tepe değeri.
Yüksüz hava aralığı akı yoğunluğunun temel bileşeni Bˆ agap1,i değerleri; hesaplamada
kullanılan tüm hesaplama düzlemleri için gerçekleştirilen FFT-algoritması yardımı
ile elde edilmektedir.
Yük durumunu dahil etmek için analiz genişletilir. Bu durumda, stator sargılarında 3faz akımı ile üretilen hava aralığı akı yoğunluğu dağılımı Bs(x) ; Fourier serileri ile
değerlendirilir.
Bs,i (x) =
⎛ px ⎞
⎛ px 2π ⎞
⎛ px 2π ⎞⎪⎫
μ0 ∞ 2Nsqξn ⎪⎧
⎨ia cos ⎜ n ⎟ + i b cos ⎜ n + ⎟ + ic cos ⎜ n − ⎟⎬ (6.21)
∑
g ' n =1 πn ⎩⎪
3 ⎠
3 ⎠⎭⎪
⎝ ri ⎠
⎝ ri
⎝ ri
Burada;
q; Kutup ve faz başına oluk sayısı,
p; Kutup çiftlerinin sayısı,
ξ n ; Stator sargı faktörü,
ia, ib ve ic ; Faz akımlarının ani değerleridir.
78
Bu durumda, harmonik sırası olan n aşağıdaki eşitlik ile hesaplanmaktadır:
n = 1 ± 2mk ,
Burada;
k = 0, 1, 2, 3,…
Stator sargı faktörü ξ n aşağıdaki gibi tanımlanır;
⎛ w π⎞ ⎛ n π⎞
2sin ⎜ n c ⎟ sin ⎜
⎜ τp 2 ⎟ ⎝ m 2 ⎟⎠
⎝
⎠
ξn =
Q
⎛ P⎞
sin ⎜ nπ ⎟
mp
⎝ Q⎠
(6.23)
Burada;
Q ; Bir statordaki oluk sayısı,
m; Faz sayısı,
wc ; Adım sayısı.
yaklaşım; endüvi reaksiyonu alanı için adımlı hava aralığı akı yoğunluk dağılımı
oluşturur. Ardından, kalıcı mıknatıs ve stator akımları tarafından üretilen hava aralığı
akı yoğunluk dağılımının bağımsız olduğu varsayılır. Bu varsayıma bağlı olarak,
endüvi reaksiyonunu içeren hava aralığı akı yoğunluk dağılımı; BPM(x) dağılımınının
Bs(x) dağılımına eklenmesi ile gerçekleştirilir:
∼
Bagap (x) = [BPM,i (x) + Bs,i (x)] λ(x)
(6.24)
79
6.2.4. Yüksüz faz gerilimi hesabı
Kalıcı mıknatısta indüklenen zıt emk’nın temel bileşeninin RMS değeri; önemli bir
tasarım niceliğidir. Zıt EMK değeri; doğrudan makine tarafından üretilen tork ile
orantılıdır. Dahası, yüksüz faz gerilimi ile faz akımı arasındaki etkileşim; bu
büyüklükler sinüsoidal değil ise bazı tork dalgacıkları üretebilir.
Bu nedenle, sadece indüklenen zıt EMK RMS değeri değil harmoniklerin de göz
önünde bulundurulması gerekmektedir. Analizde kullanılan yüksüz faz gerilimi
hesaplama metodu açıklanmıştır.
Makina; generatör olarak çalıştırıldığında, yüksüz faz gerilimi; sadece kalıcı
mıknatıslar tarafından oluşturulan akılar tarafından üretilir ve hava aralığı akı
yoğunluk dağılımına bağlı olarak değerlendirilir ;
ei,PM (t) = − N ph ξ1
ΔΦi,PM
Δt
(6.25)
Burada, Nph ; faz başına seri olarak bağlı sargıların spir sayısı, ξ1 ; temel dalganın
sargı faktörü, Φ i ,PM ; hava aralığı akısıdır.
Φi,PM =
ls
τp,i N
∫ ∫ Bagap,i (x)dxdl
(6.26)
0 0
Ardından, makinenin yüksüz faz gerilimi ePM (t ) aşağıdaki gerilimden hesaplanır:
N
ePM (t) = ∑ ei,PM (t)
i =1
(6.27)
80
Bu konunun daha önceki bölümlerinde, zıt EMK’nın dalga şeklinin hesaplanması
üzerine odaklanılmıştı. Faz sargısının boyutlandırılması için, sipir sayısı bilinen
makinanın indüklenen zıt-EMK’sının büyüklüğü ile karşılaştırıldığında (ya da
alternatif olarak istenen zıt EMK büyüklüğünü elde etmek için gerekli olan sipir
sayısı), dalga şekli çok önemli değildir. Böylece, indüklenen zıt-EMK’nın RMS
değerini hesaplamak yeterli olacaktır. Bilinen geometri ve bilinen hava aralığı akı
yoğunluğu B̂agap1 temel bileşeni ile, eşitlik (6.20)’ye göre indüklenen zıt EMK’nın
RMS değeri:
E ph,PM =
4fξ1N ph Bagap τp,ave ls
2
(6.28)
6.2.5. Vuruntu Torku
Kalıcı mıknatıslı makine tasarımı için, vuruntu torku minimize etmek; hedeflerden
birisidir. Konunun literatürü; birkaç minimizasyon metodu ortaya koymakta ve
eksenel akılı PM makineleri ilgilendiren literatürün gözden geçirilmesi; Parviainen
vd. tarafından gerçekleştirilmiştir [34]. Farklı mıknatıs şekillerinin hızlı bir analizini
elde etmek için, tasarım aracına vuruntu momenti hesaplanması dahil edilmiştir.
Vuruntu torku; her hesaplama düzlemi için yüksüz hava aralığı akı yoğunluk
dağılımından hesaplanır [35].
Tcog,i (θ) =
⎞
∂W
1 ∂ ⎛
2
⎜ ∫∫∫ Bagap,i
=
dV ⎟
⎟
∂θ 2μ0 ∂θ ⎜⎝ V
⎠
Burada;
V ; hava aralığı hacmi
θ ; rotorun açısal pozisyonu
(6.29)
81
Makinenin tamamı tarafından üretilen vuruntu torku; yüksüz durumda yapılanlarla
aynı şekilde elde edilir.
N
Tcog (θ) = ∑ Tcog,i ( θ )
(6.36)
i =1
Vuruntu torkunun hesaplanması esnasında, her hesaplama düzlemi için akı yoğunluk
dağılımının hesaplama düzleminin derinliği yönünde değişmediği varsayılmıştır.
Vuruntu torkunun analitik hesaplanması 3D FEA ile doğrulanmaktadır. Makine
tarafından üretilen vuruntu torkunu değerlendirebilmek için bir dizi manyetostatik
problem çözülür.
6.2.6. Faz direnci ve bakır kayıplarının hesaplanması
Düşük hızlı makinelerde, tüm kayıplar içinde Joule kayıpları olarak ta bilinen bakır
kayıpları genellikle baskındır. Bu yüzden, motor faz dirençlerinin düzgün tahmin
edilmesi gerekmektedir. Bir bakır telin direnci; sıcaklık bağımlılığını gösterir.
Analizde, DC direnci eşitliğe bağlı olarak hesaplanmaktadır.
R ph,DC =
lCU (1 + k cu (T − 20))
σcu Scu a
Burada;
lCu : Faz sargısının toplam uzunluğu
T : Co olarak sargının ortalama sıcaklığı
kCu : Bakır özdirencinin sıcaklık katsayısı ( kCu = 3.8 × 10 −3 1/Co )
σ Cu : 20 Co sıcaklıkta bakırın elektrik iletkenlik
S Cu : Bakırın kesit alanı
a: Paralel kol sayısı
(6.31)
82
lCu : Faz sargısının toplam uzunluğu aşağıdaki eşitliğe göre hesaplanır [26]:
(
lcu = 2N ph ls + ( 0.083p + 1.217 ) τp,ave + 0, 02m
)
(6.32)
AC-akım için, alternatif akımın sebep olduğu deri etkisi ve yakınlık etkisinden dolayı
direnç değeri DC-akımdan daha büyüktür. Bundan başka, oluklardaki kaçak akılar;
iletkenlerde ek eddy akımları oluşmasına neden olur. Bu durumdan dolayı, faz
direnci arttırılır ve aşağıdaki gibi bir yaklaşımda bulunulabilir [32]:
R ph
⎛ 1 ⎛ y ⎞2 ⎛ d ⎞2 ⎞
≈ R ph,DC ⎜ 1 + ⎜ ⎟ ⎜ w ⎟ ⎟
⎜ 9⎝χ⎠ ⎝ χ ⎠ ⎟
⎝
⎠
(6.33)
Burada;
y: Oluğun derinliği,
d w : Tek bir iletkenin çapı,
χ : Boşlukta iltkenin deri derinliği.
(6.33) eşitliği; sadece oluk şekli dikdörtgen ve oluğun derinlik doğrultusundaki
iletken sıralarının sayısı beş ya da daha fazla ise geçerlidir [32]. Boşluktaki deri
derinliği χ aşağıdaki gib tanımlanır:
χ=
2
ωμσcu
Burada;
ω ; Açısal frekans.
(6.34)
83
1.0 mm’lik tipik tel çapına sahip yuvarlak iletkenler kullanılarak sarılan düşük hızlı
makineler göz önünde bulundurulduğunda, faz sargısının AC direnci; DC faz direnci
ile pratikte aynıdır. Bu yüzden, Eş. 6.31 genellikle faz direncini hesaplamada yeterli
derecede doğru olup hesaplama modelinde kullanılır.
Hesaplanan faz akımı ve faz direncine bağlı olarak, bir stator sargısındaki bakır
kayıpları ş şekilde hesaplanır:
Pcu = mR ph I2ph
(6.35)
m ; Faz sayısı,
l ph ; Faz akmının RMS değeridir.
6.2.7. Demir kayıplarının hesaplanması
Demir kayıplarının doğru hesaplanması; demir kaybının lamine edilmiş ortamda
oluşmasından meydana gelen karmaşık olaylardan dolayı zor bir iştir. Çelik
mazemenin materyal özellikleri, akı yoğunluğunun doğal olarak değişimi (değişen,
dönme, sinusoidal, trapezoidal), laminasyon ve demetin üretim işlemi gibi özellikler
demir kayıplarını etkilemektedir. Yüzey yerleştirmeli kalıcı mıknatıslı makinelerin
demir kayıplarının miktarını tahmin etmek amacıyl birkç çalışma yapılmıştır. Yakın
zamanda Heikkilä tarafından bir değerlendirme yapılmıştır [36]. Laminasyonlardaki
demir kayıplarını bulmak için kullanılan klasik eşitlik [37]:
PFe =
⎛
k Fe,y P1.0G y B2y ⎜
1.5
f ⎞
⎟
⎝ 50 ⎠
⎛
+ k fe,t P1.0G t B2t ⎜
1.5
f ⎞
⎟
⎝ 50 ⎠
Burada;
k Fe , y ve k Fe,t
boyunduruk ve diş için bulunmuş deneysel kayıp katsayıları
P1.0
50 Hz ve 1.0 T akı yoğunluğunda çeliğin kayıp değeri
(6.36)
84
G y ve Gt
Boyunduruk ve dişlerin kütleleri
B̂ y ve B̂t
Boyunduruk ve dişlerdeki tepe akım yoğunluk değerleri
f
Ttemel elektrik frekansı
Alternatif bir yaklaşım da demir kayıplarını aşağıda sınıflandırıldığı gibi üç parçaya
bölmektir:
•
Hysteresis kayıpları
•
Eddy akımı kayıpları
•
Aşırı kayıplar (düzensiz kayıplar olarak da bilinir)
Yukardaki sınıflandırmaya göre, demir kayıplarını birim hacim başına aşağıdaki gibi
hesaplamak mümkündür [38]:
PFe = k hys B2 f + π2
σ Fe d 2
(Bf ) 2 + 8.67k ex (Bf )1.5
6
(6.37)
Burada;
k hys
hysteresis kayıp katsayısı
kex
aşırı kayıp katsayısı
d
kullanılan çeliğin kalınlığı
σ Fe
laminasyon materyalinin elektriksel iletkenliği
Histerezis kayıp katsayısı k hys ve aşırı kayıp katsayısı kex ; akı yoğunluğunun bir
fonksiyonu olarak farklı frekanslarda ölçülen kayıp eğrilerine bağlı olarak bulunur.
Genellikle, bu eğriler; çelik üreticisi tarafından sağlanır. Eş. 6.37’de, yüzey
yerleştirmeli PM makineler için akı yoğunluğunun değişimi tipik olarak trapez
şeklinde iken, demirde akı yoğunluğunun sinüsoidal olarak değiştiği varsayılmıştır.
85
Akı yoğunluğunun sinüs olmadığı durum dikkate alınarak değiştirilen Eş. 6.27 şu
şekilde olacaktır:
2
1.5
T
T
1
1 ⎛ σFe d 2 ⎛ dB ⎞
⎛ dB ⎞ ⎞
2
⎜
=
+
+
P
dt
k
B
f
(t)
k
(t)
Fe
hys
ex ⎜
⎜
⎟
⎟ ⎟⎟ dt
T ∫0
T ∫0 ⎜⎝ 12 ⎝ dt
⎠
⎝ dt
⎠ ⎠
(6.38)
(6.38) eşitliği; T zaman peryodundaki integrasyonu içermektedir, hesaplama; tam bir
döngüde gerçekleştirilir ve özellikle sonlu elemanlar metoduyla kullanılan en uygun
hesaplamadır, çünkü Eş. 6.38’de verilen eşitlik dB/dt terimine bağlıdır. Bu yüzden,
hesaplama modeli; makinenin bir kısmında yüksek doğrulukla dinamik akı davranışı
tanımını etkin hale getirir.
Trapez akı yoğunluk değişiminin sebep olduğu demir kayıplarını analitik olarak
hesaplamak için, Deng tarafından türetilen trapez akı yoğunluk dalga şekli demir
kaybı modeli kullanılabilir [38]. Model; diş genişliğine bağlı olarak α tt farkı mıknatıs
genişlikleri için akı yoğunluk dağılımına bağlıdır.
(a)
(b)
Şekil 6.7. Diş akı yoğunluğu dalga şekilleri [38].
(c)
86
Şekil 6.7’ de gösterilen basitleştirilmiş akı yoğunluğu dalga şekilleri kullanılarak,
stator dişleri için aşağıdaki demir kaybı eşitlikleri türetilebilir [38].
3/4
⎧⎛
2 2 2
3/2 ⎞
⎛
⎞
⎪⎜ khysfB2t + 2πd f Bt + kex ⎜ 4 ⎟ fBt
⎟ Gt , eğer αtt ≤ π 1−αp
⎪⎜
3ρFeαtt
παtt ⎠
⎟
⎝
⎪⎝
⎠
PFe,t ⎨
3/4
2 2 2
⎪⎛
3/2 ⎞
⎛ 4 ⎞
2
d
f
B
π
2
3/4
t
t
⎟ Gt , eğer αtt π 1−αp
k
fB
+ kex ⎜
⎪⎜ khysfBt +
⎟
l
3ρFeαtt
⎟
⎪⎩⎝⎜
⎝ παtt ⎠
⎠
( )
( )
(
)
(
)
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎭⎪
(6.39)
Burada;
ρ Fe ; Laminasyon materyalindeki yoğunluk
k1 ; Katsayısı aşağıdaki şekilde tanımlanır (6.39);
k1 = 2 −
(
π 1 − αp
α tt
)
(6.40)
Eş. 6.39’da kullanılan maksimum akı yoğunluğu; relüktans ağ çözümünden elde
edilmektedir. Eş. 6.39 ve 6.40 ifadelerinde, diş genişliğinin elektriksel radyan olarak
ifade edilmesi gerektiğini unutmayınız. Bir stator boyunduruğundaki demir kayıpları
ifadesi; Şekil 6.8’ de gösterilen akı yoğunluk dağılımına bağlı olarak türetilebilir.
87
Şekil 6.8. Boyunduruk akı yoğunluk dalga şekli [38].
Buna ilişkin demir kaybı eşitliği;
PFe,y
⎛
⎛ 8
4πd 2f 2 B2t
⎜
= k hys fB2t +
+ k ex ⎜ 2
⎜
⎜
3ρFe α tt
⎝ π α tt
⎝
⎞
⎟⎟
⎠
3/4
3/2 ⎞
( fB )
y
⎟G
⎟ y
⎠
(6.41)
Analitik yaklaşımda, eksenel-akılı PM makine; boyunduruk ve diş parçalarına
bölünür ve demir kayıpları şu şekilde hesaplanır:
N
N
i =1
i =1
PFe = ∑ PFe,y,i + ∑ PFe,t,i
(6.42)
Burada ayrıca kaçak yük kayıpları adı verilen ek demir kayıpları da görünmektedir.
Kaçak yük kayıpları; AC makinelerin ferromanyetik nüvesinde geçirgenliğe göre
değişen indüklenmiş yüksek frekanslı kayıplar ve diğer düzensiz elektromanyetik
kayıplardır. Kaçak yüklerin hesaplanması zordur ve tatmin edici doğru değerler
garanti edilmez [26].
Kaçak yük kayıpları Pstr ; genellikle çıkış gücünün bir parçası olarak göz önünde
bulundurulurlar:
88
Pstr = kstr Poutput
(6.43)
Burada;
kstr ; Kaçak yük kayıpları katsayısı.
Kaçak yük kayıpları katsayısı; 10 kW’a kadar olan makineler için 0.03…0.05
aralığında, 100 kW’a kadar olan makineler için kstr = 0.005…0.01 aralığında ve daha
büyük makineler için kstr = 0.003…0.005 aralığında değişebilir. Fakat kaçak yük
kayıpları; makinenin çıkış gücüne göre quadratik bir davranış gösterir. Böylece, kstr
için istenen değerler arasındaki doğrusal interpolasyonkaçak yük kaybının
tanılanmasını daha da zor hale getirir. Kaçak yük kayıpları için daha kesin bir ifade,
bazı ölçümler yapılarak makinenin çıkış gücünün bir fonksiyonu olarak türetilebilir
(Haataja, 2003), fakat düzgün sonuçlar ölçüme bağlı olduğu için, uygun korelâsyonu
bulmak için benzer birçok makinanın üretilip test edilmesi gerekmektedir.
6.2.8. Kalıcı mıknatıslarda ve rotor demirinde eddy akım kayıpları
Düşük hızlı sabit hızlı makinelerde ana kayıp bileşenlerine bkır ve demir kayıpları
sebep olmaktadır. Ek olarak, hava aralığının akı yoğunluk dağılımının harmonik
içeriğinden dolayı kalıcı mıknatıslarda eddyakım kayıpları oluşmaktadır. Eddy akım
kayıpları; rotor diskindeki kalıcı mıknatıslar arlında da görünebilir. Bu eddy akımı
kayıp bileşenleri; temel hava aralığı alanı genellikle rotorla senkron olarak döndüğü
ve sargı dağılımındaki harmonikler ve akım dalga şeklinde bulunan zaman
harmonikleri genellikle küçük olduğu için genellikle ihmal edilir [39]. Yarı-açık
oluklu makineler için, stator oluklarının neden olduğu yüksüz eddy akımı
kayıplarının etkisi çok önemli değildir. Yüksek hızlı makineler için, bu durum farklı
olabilir ve rotor eddy akım kayıpları; toplam kayıpların önemli bir kısmını oluşturur
[40].
Önceki etmenlere bağlı olarak ve tezde tartışılan makinelerin dönme hızlarından
dolayı, analitik tasarım prosedüründe rotor eddy akım kayıplarının hesaplanması yer
89
almamaktadır. Fakat tamamen açık oluklar var ise, düşük hızlı makineler olsa bile FE
analizi ile bir rotordaki eddy akım kayıplarının hesaplanması tavsiye edilmektedir.
Gieras; kalıcı mıknatıslarda ya da kalıcı ıknatıslar altındaki katı-demir diskte bulunan
eddy akımı kayıplarını hesaplamak için analitik metotlar sunmaktadır [20].
6.2.9. Mekaniksel kayıplar
Mekaniki kayıplar; iki ana parçaya bölünebilir:
•
Sürtünme kayıpları
•
Yatak kayıpları
Sürtünme kayıpları; dönen rotorun hava ile sürtünmesinden dolayı ortaya çıkar.
Eksenel akılı makineler için sürtünme kayıpları; dönen kapalı diskler için sürtünme
faktörü korelâsyonları kullanılarak hesaplanabilir [41]. Bilinen bir sürtünme
faktörüne kf bağlı olarak, eksenel-akılı makineler için sürtünme momenti aşağıdaki
gibi hesaplanabilir:
Tf =
(
5
k f ρair πω2 rout
− rin5
)
2
(6.44)
Burada;
σ air ; Hava yoğunluğudur.
Yatak kayıpları; yatak üreticisi ya da analitik eşitlikler tarafından sağlanan
hesaplama araçları kullanılarak hesaplanabilir [26].
Pb = 3
k bG r Ω
100π
(6.45)
90
Burada;
kb ; kb = 1’den 3’e kadar değişen bir faktördür,
Gr ; Kg olarak rotorun kütlesi,
Ω ; Rotorun dönel açısal hızı.
Yatak kaybı; yatağın eksenel ve radyal yüklerine bağlıdır. Bir rotor ve iki statora
sahip eksenel-akılı makine için, rotor ve statorlar arasındaki net çekme gücü 0’a eşit
iken, rotoru düzgün bir şekilde merkezleyerek yatağın eksenel yükünü azaltmak
mümkündür. Yoksa yatak kayıpları eksenel güç bileşeninden dolayı artar. Yatağın
radyal yüklenmesi; mili içeren rotor yapısı ağırlığının bir sonucudur.
6.2.10. İndüktansların hesaplanması
Makinenin
performans
hesaplamaları
için
senkron
indüktanslar
parametrelerdir. d-q ekseni mıknatıslanma indüktansları ( Lmd , Lmq )
önemli
ve kaçak
indüktans Lσ birlikte makine moment üretme yeteneklerinin değerlendirilmesinde
kullanılan senkron indüktansları oluşturur. d- ve q-eksenlerine bağlı olarak ilgili
relüktanslar;
Ld = Lmd + Lσ
Lq = Lmq + Lσ
Burada;
Ld
d-ekseni senkron relüktansı
Lq
q-ekseni senkron relüktansı
Lmd
d-ekseni mıknatıslanma relüktansı
Lmq
q-ekseni mıknatıslanma relüktansı
(6.46)
91
kaçak indüktans
Lσ
Kaçak indüktans Lσ ; aşağıdaki kaçak katsayılarına bağlı olarak değerelendirilebilir
[26].
1.
Oluk kaçak geçirgenlik katsayısı λslot
2.
Uç bağlantı kaçak geçirgenlik katsayısı λend
3.
Diferansiyal kaçak geçirgenlik katsayısı λdif
4.
Diş ucu kaçak geçirgenlik katsayısı λtt
Katsayı eşitlikleri; oluk ve sarım geometrisine bağlıdır. Hesaplanan kaçak katsayılara
bağlı olarak kaçak indüktans Lσ aşağıdaki gibi hesaplanabilir:
N 2ph leff ⎛
⎞
lend
λ end + λ dif + λ tt ⎟
Lσ = 2μ0
⎜ λ slot +
pq ⎝
leff
⎠
(6.47)
Burada;
lend
Uç bağlantı ortalama uzunluğu
left
Stator yığınının etkin uzunluğu (left ≈ ls + 2 g )
d-ekseni için stator başına mıknatıslanma indüktansı aşağıdaki gibi hesaplanır:
L md
(
N ph ξ1
2
= mμ 0
π
πp
)
2
τp leff
g d,eff
Ve q-ekseni için aşağıdaki gibi hesaplanır:
(6.48)
92
L mq
(
N ph ξ1
2
= mμ 0
π
πp
)
2
τp leff
g q,eff
(6.49)
Eşdeğer hava aralıkları g d ,eff ve g q ,eff , stator ve rotordaki demir parçalar olduğu gibi
kalıcı mıknatısların fiziksel hava aralıklarının etkisini içermektedir, yani demir
parçalarının doyum etkisi dikkate alınır. Doyma seviyesi; stator yarıçapının bir
fonksiyonu olarak değişebildiği için, Eş. 6.48 ve Eş. 6.49’da demir parçalarını
dikkate alan ortalama bir değer ortaya konulmuştur:
N
g d,eff
l
= g '+ PM +
μ r,PM
∑ gd,Fe,i
i =1
N
(6.50)
N
g q,eff
l
= g '+ PM +
μ r,PM
∑ gq,Fe,i
i =1
N
(6.51)
Stator sayısına ve statorların paralel ya da seri olarak bağlanmasına bağlı olarak
kısmi eksenel-akılı makine için eşdeğer devre yaklaşımı kullanılarak senkron
indüktansların hesaplanması gerekmektedir. Örnek olarak, stator akısının akacağı çift
hava aralığına sahip eksenel akılı makine için, yani statorlar paralel bağlıdır, 6.48 ve
6.49 eşitlikleri kullanılmış ise, bir hava aralığının etkin uzunluğu bir faktör ile
çarpılmalıdır. Bu tarz bir makine için uygun devre gösterimi; Şekil 6.9 ’da
verilmiştir.
93
Şekil 6.9. Elektriksel olarak paralel olarak bağlı iki statoru olan eksenel akılı bir
makinenin eşdeğer devresi [1].
Stator indüktansları ortak bir M ortak indüktansı aracılığı ile bağlandığı için, eşdeğer
indüktansların makine terminallerinden belirlenmesi gerekmektedir (A-B noktaları
arası), çünkü 6.47 ve 6.49 eşitlikleri; sadece bir statoru göz önünde bulundurmakta
ve statorlar manyetik olarak bağlı ise, bağımsız statorlar arasındaki ortak bağlantı
etkisini içermemektedir. Paralel bağlı statorlar için eşdeğer indüktanslar aşağıdaki
gibi hesaplanabilir:
Ld,q,eqv =
2
L1,d,q L 2,d,q − M12,d,q
L1,d,q L 2,d,q − 2M12,d,q
(6.52)
L1d ,q ve L2 d ,q stator idüktansları arasında ortak bağlantıyı tanımlayan bir k bağlantı
sabiti oluşturarak ve stator indüktanslarının ( L1d ,q = L2 d ,q = Ld ,q ve L1σ = L2σ = Lσ )
eşit olduğu varsayılarak M 12 d ,q ortak indüktansı aşağıdaki gibi tanımlanabilir:
M12,d,q = k L1,d,q L2,d,q = kLd,q
(6.53)
Statorlar arasındaki eşit indüktansların varsayılması L1d ,q = L2 d , q ; tasarım amacı için
geçerli bir durumdur. Tamamen eşit manyetik parametrelerin elde edilebilmesi için
94
bağımsız statorlar imal etmek ve birleştirek zordur. Bununl birlikte, göz önünde
bulundurulan elektrik makineleri için tamamen eşit parametrelere ihtiyaç vardır.
Stator senkron indüktansları Ld ,q iki parçadan oluştuğu için, (kaçak indüktans Lσ ve
mıknatıslnma indüktansı Lmd , q ) mıknatıslanma indüktansları bağlı iken stator kaçak
indüktanslarının ortak bir indüktans aracılığı ile bağlı olmadığını varsaymak
uygundur. Eş. 6.53 aracılığı ile, Eş. 6.52 yeniden yazılırsa, senkron indüktansları
hesaplayacak basitleştirilmiş bir eşitlik elde edilir:
Ld,q,eqv =
L2d,q − (kLd,q )2
2Ld,q − 2kLd,q
=
L2d,q (1 − k 2 )
2Ld,q (1 − k)
=
Ld,q (1 − k 2 )
2(1 − k)
=
Ld,q (1 + k)
2
(6.54)
(6.54) eşitliğine bağlı olarak, parelel bağlı statorların senkron indüktansları; eşdeğer
bir senkron indüktansta birleştirilir. Mıknatıslanma indüktansları tamamen bağlı
iken, stator kaçak indüktanslarının ortak bir indüktans aracılığı ile bağlanmadığını ve
statorlar arasındaki indüktans mutlak değerlerinin eşit olduğunu varsaymak Eş.6.47
ve Eş. 6.49 eşitlikleri yardımı ile kuplaj sabiti k için k = Lmd ,q / Ld ,q olacak şekilde
nümerik bir değer elde edilmesine neden olur.
6.2.11. Makinenin yük açısının hesaplanması
Kaynak gerilimi, indüklenen zıt EMK ve indüktans değerleri bilindiği için, senkron
makineler için moment eşitliğine bağlı olarak makinenin yük açısını bulmak
mümkündür.
2
⎞
U ph
(Ld − Lq )
m ⎛ E ph,PM U ph
⎜
T=
sin(δ) +
sin(2δ) ⎟
⎟
Ω⎜
ωLd
2ω(Lq Ld )
⎝
⎠
Burada;
(6.55)
95
δ ; Yük açısı,
U ph ; Kaynk hat gerilimidir.
Stator resistif gerilim düşümü indüktif gerilim düşümünden büyük olan makineler
için, (6.55) eşitliğinin faz direncini içeren bir moment eşitliği ile değiştirilmesi
tavsiye edilmektedir. Bu; örneğin küçük makineler için bir durum olabilir [26].
(
)
⎧ Uph Eph,PM R ph cos(δ) + ωLd sin(δ)
⎫
⎪
⎪
2
2
2
⎪
⎪
ω Ld Lq + R ph
⎪
⎪
⎪
⎪
2
2
2
⎫⎪
⎪⎧⎡ ω Ld Lq + R ph − ω Lq (Ld − Lq ) −⎤
⎪⎪
⎦
⎪⎪⎣
⎪
⎪⎪
⎪
⎪⎪
m ⎪⎪
T = ⎨⎪U E
⎪⎬
δ
−
ω
δ
ω
−
ω
+
R
cos(
)
L
sin(
)
(
L
L
)
d
d
q
Ω ⎪⎪ ph ph,PM ph
⎪⎪⎪
⎪
⎪⎨
⎬⎪
⎪⎪ 2
⎪⎪
⎪⎪Uph Eph,PM R ph cos(δ) + ωLd sin(δ) − R ph cos(δ) − ωLd sin(δ) (ωLd − ωLq ) −⎪⎪
⎪⎪
⎪⎪
⎪⎪
⎪⎪
⎪⎪ 2
2
2
2
⎪⎪
⎪⎪ Eph R ph − [(ω Ld Lq − R ph − (ω Lq (Ld − Lq ))
⎪⎭⎪⎭
⎩⎩
(
)
(
)
(
)
(
) (
(
)
)
(6.56)
6.2.12. Verim ve güç faktörü
Bundan sonra, makinenin toplam verim ve güç faktörü gerçekleştirilir ve makine
tasarımı tamamlanır. Makine verimi; hesaplanan giriş gücü ve hesaplanan kayıplar
kullanılarak elde edilir:
η=
Poutput
Pinput
=
Pinput − Pcu − PFe − Pstr − Pb
Pinput
(6.57)
Makine güç faktörü; aktif güç ile görünür güç arasındaki ilişki kullanılarak elde
edilebilir:
96
cos ϕ =
mU ph (Iq cos δ − Id sin δ)
mU ph Id2 + Iq2
(6.58)
Burada, uygun d-q ekseni akımları aşağıdaki gibi hesaplanır:
Id =
Iq =
(
)
U ph ωLq cos δ − R ph sin δ − E ph,PM ωLq
ω2 Ld Lq + R 2ph
(
)
U ph R ph cos δ − ωLq sin δ − E ph,PM R ph
2
ω
Ld Lq + R 2ph
(6.59)
(6.60)
Hesaplanan motor parametrelerine bağlı olarak, makine çalışma noktasını bir fazör
diyagramı kullanarak resimlendirmek mümkündür. Şekil 6.10’ da, fazör diyagramı;
uyarılmış kalıcı mıknatıslı motor için gösterilmektedir.
Şekil 6.10. Uyarılmış senkron motorun fazör diyagramı. Endüvi reaksiyonunun
genellikle d-ekseni üzerinde demanyetize olduğu görülmektedir I d < 0.
97
7. TASARLANAN MAKİNA VE SİMÜLASYON SONUÇLARI
Daha önceki bölümlerde verilen teori kullanılarak prototip bir makine tasarlanmış ve
üretilmiştir. Üretilen prototip herhangi bir optimizasyon işleminden geçirilmemiştir.
Prototip makine ile, geliştirilen analitik tasarım aracı yardımıyla geliştirilen çalışma
sonuçları doğrulanmıştır. Prototip makine; bir rotor ve iki statordan oluşan eksenel
akılı kalıcı mıknatıslı bir makinedir. Statorlar; elektriksel olarak paralel ve yıldız
bağlı olarak çalışmaktadır. Bu düzenleme, statorlar arasında dengesiz yüklenmeye
neden olabilir, bu yüzden hava aralığının ayarlanması gerekmektedir. Makinenin
anma gücü 5.5 kW olup anma hızı 300 d/dk’dır.
Mıknatıslar, TEMSAN A.Ş tarafından yurtdışından özel kalıplar hazırlattırılarak
imal edilip ithal edilen Neodymium-Iron-Boron mıknatıslarıdır. Mıknatısların ST37
çeliğinden yapılmış olan katı rotor diski yüzeyine yapıştırılarak sabitlenmiştir.
Mıknatıs şekli vuruntu torkunu azaltacak geometriye sahip ve sinüsoidaldır. Stator
nüvesinin malzemesi tam işlenmiş olan elektriksel çelik M19’dur. Makinanın sarım
tipi kutup ve faz başına oluk sayısı 1’e eşit olan klasik tam kalıp sargı türüdür.
Makinenin ana parametreleri; Tablo 7.1’ de verilmiştir.
98
Çizelge 7.1. Prototip makinenin ana parametreleri
Parametre
Açıklama
Değer
P
Anma Gücü
5,5 kW
N
Anma Hızı
300 d/dk
T
Anma Torku
175 Nm
U faz
Anma Faz Gerilimi
220V
I faz
Anma Faz Akımı
9,6A
lPM
Mıknatıs Kalınlığı
5mm
GPM
Toplam Mıknatıs Ağırlığı
2,6 Kg
Ns
Stator Oluk Sayısı
36
2p
Kutup Sayısı
12
g
Hava Aralığı Uzunluğu
2x1,5 mm
D DIŞ
Stator Dış Çapı
344
D İÇ
Stator İç Çapı
215
N faz
Faz Başına Düşen Seri Sarım Sayısı
780
Prototip makine kısmi olarak laboratuar test kullanımı için tasarlanmıştır. Manyetik
demir alaşımından üretilmiş olan lamine edilmemiş rotor disk makinenin tek taraflı
olarak kullanılmasını da sağlamaktadır. Bu temele dayananak 18 mm+ mm’lik rotor
demiri kalınlığı akı yoğunluğunu rotor demirinde tutmak için yeterli bir değerdir.
Dahası, derin yivli yuvarlak yataklara sahip olan prototip makinanin mekaniksel
yapısı stator ve rotor diski arasındaki çekme gücünü kontrol altında tutmak için
yeteri kadar serttir. 1,5 mm’lik anma hava aralığı ile yük şartları altında
gerçekleştirilen 3D FEA’ya göre stator başına bu güç değeri 7,1 kN’dir. Normal
çalışma şartları altında, diğer statorun bulunmasının; stator ve rotor arasındaki net
çekme gücünü çoğunlukla ortadan kaldırdığını unutmamalıdır. Fakat üretim
şartlarından dolayı statorlar arasında dengesiz yük durumu meydana gelirse, rotor
yapısını etkileyen net eksenel güç kesinlikle 0’a eşit olmaz. Mıknatısların rotor
99
üzerindeki yerleşimi Şekil. 7.1’ de ve tek bir mıknatısın görünümü Şekil. 7.2’
gösterilmiştir.
Şekil 7.1. Rotora yerleştirilen mıknatıslar.
Şekil 7.2. Tek bir mıknatısın görünümü.
Rotoru statorlar arasında tamamen sıralayabilmek için, özel bir yatak vida somunu
düzenlemesi yapılmıştır. Milin her iki ucuna yerleştirilmiş olan yatak vida somunları
100
dış çerçeveyi açmadan makine içersinde rotor pozisyonun değiştirmeyi sağlar. Bu
yapı rotorun yanlış yerleştirilmesinin makine performansı üzerindeki etkisini
gerektiğinde düzenleyecek bir yapıdır. Prototip makinanın her iki statoru bir lazer
kesme metodu kullanılarak lamine saclardan üretilmiş ve arka yüzlerinden
sabitlenerek cıvata bağlantıları ile dış kapağa sabitlenecek şekilde üretilmiştir.
Statorların her biri 36 oluğa sahiptir.Üretim tekniğinden dolayı, elde edilen stator
laminasyon paketleme faktörü tasarım işlemi esnasında öngörülenden daha zayıftır
ve sadece 0.92’dir. Makinenin iç yarıçapında son sargının uygun boşluğa oturtulması
zaman kaybından kurtulmayı sağlamıştır. Şekil 7.3 ve 7.4 de makina statorlarından
biri sarımdan önce ve sonra olarak gösterilmiştir. Statorun imalatına yönelik teknik
resimler ve hesaplama ara yüzleri ekler kısmında sunulmuştur.
Stator sarımında, kutup ve faz başına sarım sayıları 1’e eşittir. Her sargıda 130 sipir
vardır ve faz başına düşen toplam sipir sayısı 780’dir. Stator faz sarımlarının her iki
ucunda da bir bağlantı kutusunda bulunmaktadır. Sonuç olarak, bu durum; makinenin
elektriki bağlantısını yıldızdan üçgene değiştirilmesini ve statorlar arasındaki
bağlantının paralelden seriye değiştirilmesini ya da makinenin sadece bir stator
kullanarak çalışmasını sağlayabilmektedir. Makine, stator uçları paralel olarak bağlı
iken yıldız bağlantıda çalışacak gibi tasarlanmıştır fakat makine çalışma noktası
değiştirilerek makinenin farklı bağlantılarda çalışması mümkündür.
101
Şekil 7.3. Sarımdan önce statorlardan birinin görünümü.
Şekil 7.4. Sarımdan sonra statorlardan birinin görünümü.
Şekil 7.5’ de hazırlanan statorun dış kapağa sabitlenerek montaja hazır hale gelmesi
gösterilmektedir. Şekil 7.6’ de ise tüm parçalar hazır montaja hazır hale getirilmiştir
ve görüldüğü üzere makine kabaca üç parçadan oluşmaktadır. Şekil 7.7’ de makina
montajı tamamlanmış ve test için hazır hale gelmiştir.
102
Şekil 7.5. Sarımı tamamlanmış olan statorlardan birinin yaltaklandırılarak çerçevesi
içine yerleştirilmiş hali.
Şekil 7.6. Makinanın tüm parçalarının montaja hazır halde görünümü.
103
Şekil 7.7. Montajı tamamlanan makinanın görünüşü.
7.1. İndüklenen zıt-EMK
Rotor pozisyonunu ayarlamak; her iki statorun indüklenen zıt-EMK büyüklükleri
karşılaştırılarak yapılabilir. Yatak vida somunları ile rotor pozisyonu her iki stator
için temel büyüklükler eşit olacak şekilde bir pozisyona yerleştirilir. Şekil 7.8 ve
Şekil 7.9’da yüksüz ve anma yükünde karalı durumda çalışan makina için ölçüm
sonuçları verilmiştir. İndüklenen zıt-EMK temel bileşeni için elde edilen değerler
hesaplanan değerlerle uyuşmaktadır.
104
Şekil 7.8. Makina yüksüz iken indüklenen faz gerilimleri
Şekil 7.9. Makina yüklü ve kararlı durumda çalışırken indüklenen faz gerilimleri
105
7.2. Vuruntu Torku
Prototip makine 10 d/dk hızda dönerken ve hız kontrollü DC makine motor olarak
çalıştırılırken tork 50 Nm’ lik tork transdüseri ile ölçülmüştür. Prototip makine için
dönme hızı 1 Hz’lik elektriksel frekansa denk gelmektedir. Şekil 7.10 ’de ölçülen
vuruntu torku değerleri gösterilmektedir. Şekil 7.10’ dan ölçülen vuruntu torkunun
3D FEA ile ölçülenden %90 daha büyük ve analitik hesaplamadan elde edilen
sonuçtan %50 daha büyük değerler aldığı söylenebilir.
Şekil 7.10. Ölçülen vuruntu torku
7.3. Verim
Makinanın verimi, ölçülen elektriksel ve mekaniksel güçlere bağlı olarak
hesaplanmıştır. Şekil 7.11, hava soğutmalı olarak düzenlenmiş olan makine için
motor veriminin hıza bağlı olarak grafiğini göstermektedir. Bu soğutma metodu
kısmi olarak prototip motor için birincil tasarım kriterinde bulunmaktadır.
106
Şekil 7.12, çıkış gücünün 4 kW’ ın altına düştüğünde ve gücün 6,5 kW’ın üzerine
çıktığında verimde hızlıcı bir azalma meydana geldiğini göstermektedir. Bu, kalıcı
mıknatıslı makinelerin tipik davranışları ile açıklanabilir. Kalıcı mıknatıs sıcaklığı
artarsa, kalıcı mıknatısın manyetik akı yoğunluğu azalır. Bu yüzden, orijinal stator
akı bağlantısı korunursa, statorda daha fazla bakır kaybına neden olan daha fazla
mıknatıslanma akımına ihtiyaç duyulur. Bakır kayıpları arttığında meydana gelen
sıcaklık farkı, kalıcı mıknatıs akı yoğunluğunda düşme ve faz sargısının direncinde
artmaya neden olur.
Bu olaylar stator sargısındaki güç kaybını arttırır. Çıkış gücü aşılırsa, çok hızlı bir
şekilde kendi kendine besleme olayı meydana gelir ve soğutma aynı tutulursa, çıkış
gücündeki küçük bir değişim, sıcaklıkta %10 oranında artmaya neden olabilir. Oluk
yalıtımı için izin verilen maksimum stator sarım sıcaklığı 150 Co olarak
sınırlandırılırsa maksimum çıkış gücü 7 kW olur. Diğer taraftan açıklanan olaylar
kararlı hali yakalamak için gerek duyulan zamanın uzun olmasına neden olmaktadır.
Şekil 7.11. Hızın bir fonksiyonu olarak verim değerlerinin değişimi
107
Şekil 7.12. Çıkış gücünün bir fonksiyonu olarak makinanın verimi. Anma güç
değerinden daha düşük çıkış gücü elde edilirse, verimin azalmaya
başlayacağı görülmektedir.
7.4. Diğer Makina Parametreleri
Şekil 7.13’ de hızın bir fonksiyonu olarak çıkış gücünün değişimi gösterilmektedir.
Makinanın anma gücünün üzerinde yüklenmesi durumunda kalıcı mıknatıslar
sıcaklıktan etkilenmekte ve harici bir soğutma sistemi olmadığı takdirde makina 6,5
kW değerinden sonra doyuma ulaşacaktır. Makina gücünün sıcaklığın bir fonksiyonu
olarak değişimi Şekil 7.14’ de verilmiştir. Burada makina ısısının artmasıyla çıkış
gücünün düştüğü görülmektedir. Bunun başlıca sebebi daha önceki kısımlarda da
belirtildiği üzere kalıcı mıknatısların maksimum enerjilerinin sıcaklıkla ters orantılı
olarak değişmesidir. Şekil 7.15’ de makina veriminin sıcaklıkla meydana gelen
değişimi gösterilmektedir. Sıcaklık arttıkça makina verimindeki düşüş çıkış
gücündeki düşüş oranı kadar olmasa da yinede kayda değer bir düşüş
sergilemektedir.
108
Şekil 7.13. Hızın bir fonksiyonu olarak çıkış gücünün değişimi. Makinanın anma
gücünün üzerindeki değerler makinanın harici bir soğutma sistemine
bağlandığı takdirde mümkün olmaktadır.
Şekil 7.14. Sıcaklığın bir fonksiyonu olarak çıkış gücünün değişimi.
109
Şekil 7.15. Sıcaklığın bir fonksiyonu olarak verimin değişimi.
Şekil 7.16. Yük altında indüklenen faz akımları.
110
Şekil 7.16’ da makinanın anma devir ve gücünde kararlı durumda çalışırken her üç
faz sargısında indüklenen faz akımları görülmektedir. Makina yüklendikçe elde
edilen faz akımlarının tepe dalga şekillerinin bozulduğu görülmektedir. Fakat elde
edilen dalga şekilleri kabul edilebilir sınırlar içerisindedir. Özellikle kalıcı mıknatısın
geometrisi bu dalga şeklinde önemli bir etkendir.
Şekil 7.17’de anma yükü ve hızında çalışan makinanın hava aralığı manyetik akı
yoğunluğu
değeri
görülmektedir.
Faz
akımlarının tepe dalga
şekillerinde
gözlemlenen eğriliğin hava aralığı akı yoğunluğu ifadesinde de gözlemlenmesi
gerektiği düşünülebilir fakat makina yapısının eksenel olmasından ve yerleştirilen
mıknatısların geometrilerinden kaynaklanan etkenlerden dolayı bu eğrilik faz
akımlarında olduğu kadar belirgin değildir.
Şekil 7.17. Yük altındaki makinanın hava aralığı manyetik akı yoğunluğu
111
Tasarlanan makinada hesaplanan mıknatıs kalınlığı ifadelerinin çıkış gücüne etkisi
dikkate alınmış ve mıknatıs kalınlığının çıkış gücüne etkisi parametrik olarak
hesaplanarak optimum çıkış gücünü sağlayan mıknatıs kalınlığı seçilmiştir.
Şekil 7.18’de her bir mıknatıs kalınlığına karşılık gelen güç-hız eğrileri
gösterilmiştir. Burada mıknatıs kalınlığının 5mm olduğu eğri makinanın güç-hız
eğrisini göstermektedir.
Şekil 7.18. Hızın bir fonksiyonu olarak mıknatıs kalınlıklarına karşılık gelen çıkış
gücü değerleri
7.5. Özet
5,5 kW’ lık bir EAKM makina tasarlanmış ve üretilmiştir. Prototip makinenin
hesaplanan ve ölçülen değerlerinin karşılaştırıldığında genellikle uyumlu bir tablo
çizdiği görülmektedir. Yüksek performanslı yüzey yerleştirmeli kalıcı mıknatıslı bir
makina amaçlanıyorsa, kalıcı mıknatısların yerleştirilmesi sırasında doğrudan
hizalanmaması tavsiye edilmektedir.
112
Bu çalışmada elde edilen sonuçlara bağlı olarak, geliştirilen analitik tasarım
yönteminin yüzey yerleştirmeli eksenel akılı kalıcı mıknatıslı makinaların
tasarımında yeterli derecede bir doğruluk gösterdiği ve diğer benzer yapıdaki eksenel
akılı kalıcı mıknatıslı makinaların tasarımı için kabul edilebilir değerler arasında
olduğu ifade edilmektedir.
113
8. SONUÇLAR VE ÖNERİLER
Bu çalışmanın ilk amacı tek rotor çift stator düzenlemeli eksenel akılı yüzey
yerleştirmeli kalıcı mıknatıslı makinanın analitik ve bilgisayar destekli sonlu
elemanlar yöntemi ile tasarımının gerçekleştirilmesidir. Çalışmada makinanın
analitik olarak boyutlandırma ve elektromanyetik parametrelerinin oluşturulmasına
yönelik hesaplamalar yapılmış ve bu değerlere göre elde edilen boyutlandırma
değerleri Ansoft firmasının Maxwell yazılımı ile bilgisayar destekli olarak üç
boyutlu (3D) modellenerek analiz ve iyileştirme çalışmaları yapılmıştır.
Makinanın üretim sürecinde bazı zorluklar (örneğin stator nüvesinin imalatı)
olmasına rağmen geliştirilen bazı hesaplama yazılımları vasıtası ile olabildiğince bu
problem ortadan kaldırılmıştır. Makinanın uyartımında kullanılan kalıcı mıknatısların
boyutlandırılması için de vuruntu torku dikkate alınarak ayrı bir hesaplama yöntemi
oluşturulmuş ve elde edilen değerlere göre mıknatıslar yurtdışında özel kalıplar
yaptırılarak imal edilmiştir. (Ortalama bir mıknatısın maliyeti 30 €)
Üretimden kaynaklanan birkaç küçük hatanın dışında ölçülen değerler hesaplanan
değerlerle yakın değerler almıştır. Bu da kullanılan hesaplama yöntemi ile elde
edilen sonuçlar arasında iyi bir düzenlemenin olduğunu göstermektedir. Makina
malzeme maliyetleri bakımından diğer makinalar ile karşılaştırıldığında bazı özel
teknik masraflarının dışında maliyetlerin yaklaşık olarak aynı olduğu söylenebilir.
Eğer sadece makinadaki aktif malzemeler bakımından karşılaştırılma yapılacak
olursa, eksenel akılı kalıcı mıknatıslı iç rotorlu makina, kutup sayısının büyük olduğu
2p ≥16 düzenlemelerde daha az bir maliyete sahiptir. Eksenel akılı kalıcı mıknatıslı
makinalarda gerekli mıknatıs miktarı radyal akılı makinalara oranla daha azdır, diğer
taftan gerekli bakır miktarı ise doğal olarak daha fazla olmaktadır. Toplam
elektriksel sac bakımından karşılaştırıldığında ise bu makina yapısında radyal akılı
makinalara oranla daha az sac tüketimi gerekmektedir.
114
Sonuç olarak eksenel akılı kalıcı mıknatıslı makinalar, radyal akılı makinaların
geometrik olarak sınırlı kaldığı uygulamalarda dikkat çeken bir çözüm olarak
karşımıza çıkmaktadır. Özellikle radyal akılı makinalarla uzunluk oranları (stator
yığınının uzunluğuna karşılık hava aralığı çapı) bakımından karşılaştırıldığında bu
değer 0,5’ in altında çıkmaktadır. Eksenel akılı kalıcı mıknatıslı makinalarda genel
olarak istenilen verim değerini yakalayabilmek için gerekli akım yoğunluğu değeri
daha azdır.
Eksenel akılı kalıcı mıknatıslı makinalar geliştirilmeye açıktır. Bu makinaların
üretim ve tasarım tekniklerinin geliştirilmesi, bu alanda ticari olarak yapılacak
çalışmaların da sayılarının hızla artacağını göstermektedir. Böylelikle her bir
makinanın birim maliyetinin düşeceği ve pek çok uygulama için tercih sebebi
olabileceği söylenebilir.
115
KAYNAKLAR
[1] Parviainen, A. “Desıgn Of Axıal-Flux Permanent-Magnet Low-Speed Machınes
And performance Comparıson Between Radıal-Flux And Axıal-Flux Machınes”
Diss. Lappeenranta University of Technology, PhD thesis (2005).
[2] Gieras, J. F., Wang, R. J., Kamper, M. J., “Axial Flux Permanent Magnet
Brushless Machines”, Kluwer Academic Publisher, 341, (2004).
[3] Kazım, Y. “Sürekli Mıknatıslı Senkron Motor Tasarımı ve Analizi” , Doktora
tezi, Kocaeli Üniv.F.B.E, (1999).
[4] Diril, O. “Sürekli Mıknatıslı Senkron Motor” , Yüksek Lisans Tezi, İTÜ Fen
Bilimleri Enstitüsü, (1989) .
[5] Kurt, Ü. “Eksenel Akılı Sürekli Mıknatıslı Senkron Makinalar İçin Yeni Tasarım
Modeli Geliştirme” , Doktora Tezi, Ondokuz Mayıs Üniversitesi, FBE, (2006).
[6] Chan, C.C. “Axial-Field Electrical Machines-Design And Applications” , IEEE
Transaction On Energy Conv. 2(2): 294-300, (1987).
[7] Nasar, S. A., Xiong, G. “Determination Of The Field Of A Permanent-Magnet
Disk Machine Using The Concept Of Magnetic Charge”, IEEE Transaction on
magnetic, 24(3): 2039-2044, (1988).
[8] Spooner, E., Chalmers, B.J., “TORUS’ a Slotless, Toroidal-Stator,PermanentMagnet Generator” , IEE Proc., 139(6): 497-506, (1992).
[9] Chalmers, B. J., Spooner, E., Honorati, O., Crescimbini, F., Caricchi, F.,
“Compact Permanent-Magnet Machines”, Taylor & Francis, 25: 635-648,
(1997).
[10] Chalmers, B. J., Gren, A. M., Reece, A. B. J., Al-Babi, A. H., “Modelling and
Simulation of Torus Generator” , IEE Proc.-Electr. Power Appl., 144(6): 446452 , (1997).
[11] Zhilichev, Y., “Three-Dimensional Analytic Model Of Permanent Magnet Axial
Flux Machine” , IEEE Transaction on Magnetic, 34(6): 3897-3901, (1998).
[12] Huang, S., Luo, J., Leonardi, F., Lipo,T.A., “A Comparison of Power Density
for Axial Flux Machines Based on General Purpose Sizing Equations” , IEEE
Transac.on Energy Conversion, 14(2): 185-192, (1999).
[13] Muljadi, E., Butterfield, C.P., Wan, Y., “Axial Flux Modular Permanent-Magnet
Generator with a Troidal Winding for Wind-Turbine Applications” , IEEE
116
Industry Applications Conference St.Louis, MO November, 5(8): 831-836,
(1999).
[14] El-Hasan, T. S., Patrick, C. K., Modular Design of High-Speed Permanent
Magnet Axial-Flux Generators, IEEE Transaction on Magnetic, 36(5): 35583561, (2000).
[15] Mbidi, D. N., Wang, R., Kamper, M.J., Blom, J., Mechanical “Design
Considerations Of A Double Stage Axial-Flux PM Machine” , IEEE, ID 07803-6401-5/00 :198-201, (2000).
[16] Aydın, M., Huang, S., Lipo,T.A., “Design And 3D Electromagnetic Field
Analysis Of Non-Slotted And Slotted TORUS Type Axial Flux Surface
Mounted Permanent Magnet Disc Machines”, IEEE, ID 0-7803-7091-0/01
:645-651 , (2001).
[17] Sitapati, K., Krishnan, R., “Performance Comparisons Of Radial And Axial
Field, Permanent-Magnet, Brushless Machines”, IEEE Trans.on Ind.Appl.,
37(5): 1219-1225, (2001).
[18] Braid, J., Zyl, A., Landy, C., “Design, Analysi And Devolopment Of A
Multistage Axial-Flux Permanent Magnet Synchronous Machine”, IEEE
Africon 2002, : 675-680, (2002).
[19] Bumby, J. R., Mueller, M.A., Spooner, E., Brown N. L., Chalmers, B. J.,
“Electromagnetic Design Of Axial-Flux Permanent Magnet Machines”, IEE
Proc.-Electr.Power Appl., 151(2): 151-160, (2004).
[20] Gieras, J. F., Wang, R. J., Kamper, M. J., “Axial Flux Permanent Magnet
Brushless Machines”, Kluwer Academic Publisher, :341, (2004).
[21] Parviainen, A., Pyrhönen, J., Niemala M., “Axial Flux Interior Permanent
Magnet Synchronous Motor With Sinusoidaly Shaped Magnets” , ISEF 2001,
(2001).
[22] Caricchi, F.,Crescimbini, F., Honorati, O., Bianco. L.G., Santini, E.,
Performance of Coreless-Winding Axial-Flux Permanent-Magnet Generator
With Power Output at 400 Hz, 3000 r/min”, IEEE Transaction on Industry
.Application. 34(6): 1263-1269, (1998).
117
[23] Furlani, E. P., “Permanent Magnet And Electromechanical Devices”, Academic
press. :513, (1996).
[24] Essam, S.H., “Design of Small Electrical Machines”, John Wiley & Sons. İnc.
:53-60, (1994).
[25] Rasmussen, C.B., Ritchie, E., “A magnetic Equivalent Circuit Approach for
Predicting PM Motor Performance”, In Proceedings of IEEE Industry
Applications Conference, IAS Annual Meeting, : 10-17, (1997).
[26] Gieras, J.F., Wing, M., “Permanent Magnet Motor Technology Design and
Applications”, Marcel Dekker Inc, New York, :444, (1997).
[27] Perho, J., “Reluctance Network for Analysing Induction Machines”,
Dissertation Helsinki University of Technology, Finland,, : 147, (2002).
[28] Hwang, C-C., Cho, Y.H., “Effects of Leakage Flux on Magnetic Fields of
Interior Permanent Magnet Synchronous Motors”, IEEE Transactions on
Magnetics., 37(4): 3021-3024, (2001).
[29] Qu, R., Aydin, M., Lipo, T.A., “Performance Comparison of Dual-Rotor RadialFlux and Axial-Flux Permanent-Magnet BLDC Machines”, In Proceedings of
IEEE Electric Machines and Drives Conference, IEMDC'03, Madison,
United States, 1-4 June 2003, 3: 1948-1954, (2003).
[30] Zhu, Z.Q., Howe, D., Bolte, E., Ackermann, B., “Instantaneous Magnetic Field
Distribution in Brushless Permanent Magnet DC Motors”, Part I: OpenCircuit Field. IEEE Transaction on Magnetic, 29: 124-135, (1993).
[31] Chung, M-J., Gweon, D-G., “Modeling of the Armature Slotting Effect in the
Magnetic Field Distribution of a Linear Permanent Magnet Motor”, Electrical
Engineering - Archiv für Elektrotechnik, 84: 101-108, (2002).
[32] Hanselman, D. C., “Brushless Permanent Magnet Motor Design”, New York:
Elsevier Scientific Publishing Company, : 330, (2003).
118
[33] Zhu, Z. Q., Howe, D., “Analytical Prediction of the Cogging Torque in RadialField Permanent Magnet Brushless Motors”, IEEE Transaction on Magnetics,
28: 1371-1374, (1992).
[34] Parviainen, A., Niemelä, M., Pyrhönen, J., “Reduction of Torque Pulsations in
Axial-flux Interior PM Synchronous Machines”, In Proceedings of Nordic
Workshop on Power and Industrial Electronics, Stockholm, Sweden, 12-14
August 2002, on CD-ROM, (2002b).
[35] Barakat, G., El-meslouhi, T., Dakyo, B., “Analysis of the Cogging Torque
Behavior of a Two-Phase Axial-flux Permanent Magnet Synchronous
Machine”, IEEE Transactions on Magnetics, 37(4): 2803-2805, (2001).
[36] Heikkilä, T., “Permanent Magnet Synchronous Motor for Industrial Inverter
Applications Analysis and Design. Dissertation”, Lappeenranta University of
Technology, Finland, :109, (2002).
[37] Vogt, K., Elektrische Maschinen. Berlin: VEB Verlag Technik, : 500, (1983).
[38] Deng, F., “An Improved Iron Loss Estimation for Permanent Magnet Brushless
Machines”, IEEE Transactions on Energy Conversion, 14(4): 1391-1395,
(1999).
[39] Atallah, K., Howe, D., Mellor, P. H., Stone, D. A., “Rotor Loss in PermanentMagnet Brushless AC Machines”, IEEE Transactions on Industry
Applications, 36(6): 1612- 1618, (2000).
[40] Sahin, F., “Design and Development of a High-Speed Axial-Flux PermanentMagnet Machine, Dissertation”, Eindhoven University of Technology, The
Netherlands, :228, (2001).
[41] Daily, J.W., Nece, R.E., ”Chamber dimension effects on induced flow and
frictional resistance of enclosed rotating disks”, Journal of Basic Engineering,
82: 217-232, (1960).
119
EKLER
120
EK-1 Prototip makinada imalatında kullanılan teknik resimler
Şekil 1.1. Stator Sarım Şeması.
121
EK-1 (Devam) Prototip makinada imalatında kullanılan teknik resimler.
Şekil 1.2. Stator saclarının her birinin boyutlarını hesaplayan analitik ara yüz.
122
EK-1 (Devam) Prototip makinada imalatında kullanılan teknik resimler.
Şekil 1.3 Kalıcı mıknatısın geometrik olarak boyutlandırmasını sağlayan analitik ara
yüz.
123
EK-1 (Devam) Prototip makinada imalatında kullanılan teknik resimler.
Şekil 1.4 Şekil 1.2 deki ara yüze göre boyutlandırılan stator laminasyonlarının bir
bölümü.
124
ÖZGEÇMİŞ
Kişisel Bilgiler
Soyadı , adı
: OCAK Cemil
Uyruğu
: T.C.
Doğum tarihi ve yeri : 12/02/1985 İZMİR
Medeni hali
: Bekar
Telefon
: 0 505 639 90 76
e-mail
: cemilocak@gmail.com
Eğitim
Derece
Eğitim Birimi
Mezuniyet Tarihi
Lisans
Gazi Üniversitesi / Elektrik Eğitimi Bölümü
2007
Lise
İzmir Çınarlı Teknik Lisesi
2002
Yabancı Dil
İngilizce