A)1 B)2 C)3 0)4 2.

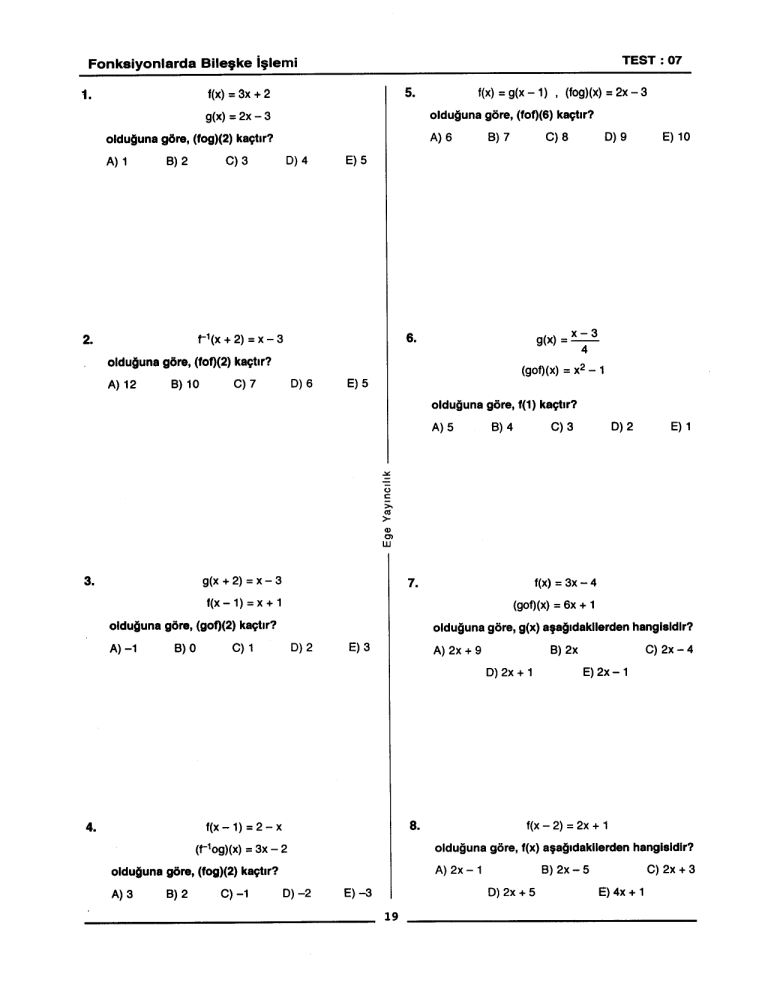
= 3x + 2
g(x) = 2x - 3
1.
f(x)
f(x)
olduguna
A)1
B)2
= 2x -
3
olduguna gore, (fof){6) ka~lr?
C)3
r1(x + 2) = x A)12
1) , (fog)(x)
gOre, (fog){2) ka~tlr?
2.
olduguna
= g(X -
0)4
x-3
g(x) =-4
6.
3
gore, (fof){2) ka~tlr?
B)10
C)7
(gof)(x) = x2 - 1
0)6
E) 5
olduguna gore, f(1) ka~lr?
A)5
B) 4
0)2
C)3
E) 1
.>0:
0
C
>-
<ll
>Q)
Cl
w
g(x + 2) = x - 3
3.
f(x -1)
olduguna
A) -1
(gof)(x) = 6x + 1
gore, (gof){2) ka~tlr?
B) 0
f(x) = 3x - 4
7.
=x + 1
C)1
olduguna gore, g{x) a,agldakllerden
0)2
E) 3
A) 2x + 9
B)2x
0) 2x + 1
f(x - 1)
(t"1og)(X)
=2- X
= 3x - 2
olduguna gOre, (fog){2) ka~tlr?
C) 2x - 4
E) 2x-1
f(x - 2)
olduguna
hanglsldlr?
= 2x + 1
gore, f(x) a,agldakllerden
A) 2x - 1
hanglsldlr?
C) 2x + 3
B) 2x - 5
0) 2x + 5
E) 4x + 1
f (x + 1 )
x-1
= 2x -
(fog)(x) = 2x2
2
x+1
g(x)
olduguna
B) ~
x
=x
2 -
E) 2x
(fog)(x)
= 4x2 -
(g)(x) = 2x2
olduguna
dir?
olduguna gore, (gof)(x)
lerden hanglsldlr?
fonkslyonu
6
3
-
gore, f(2x) In f(x) clnslnden
A) 2f(x)
a!;agldakl-
hanglsldir?
B) 2x - 3
D) 2x - 5
2
2x
gore, f(x) a!;agldakilerden
A) 2x + 3
D)K.
4x + 3
-
degerl ne-
B) 4f(x)
E) f(x)
D) 2f(x) - 1
2
B) 4x + 7
A) 4x-1
E) 4x + 3
D) 4x - 3
= 2x
f(x)
+ U
x +1
(fof)(x) = x - 9
3x - 2
f(x) = 5x - 3 • g(x) = 4x + a
11.
1~ln (fog-1)-1(2)
fonkslyonlarl
= 0 olduguna
gore,
a ka~tlr?
16.
f
= (1 234)
ve
2341
12.
f(2x - 1)
olduguna
A) 3
= g(x
+ 1)
C) 5
234)
3142
veriliyor.
a = (gof)(3) ve b = (g-10f)(1)
gore, (g-10f)-1(4) ka~t1r?
B) 4
9 = (1
olduguna
gore, a . b ka~tlr?
E) 7
D)6
20
11.E
2.A
3.A
4.E
5.8
6.C
7.A
8.D
9.A
10.A
11.8
12.C
13.A
14.A
15.A
16.D
I
y
= f(x + 1)
fonksiyonunun
grafigi verilmi~tir.
Buna gore,
Verllenlere gore, (fo1)(-2) + t"1(-2) + f(O) toplaml
ka(:t1r?
f(x) va g(x) fonksiyonlannm grafigi verilmi~tir.
Buna gore, g(-3) + (fog)(-1)
f-1 (2)
degeri ka(:tlr?
Yukanda verilen f(x) fonksiyonunun grafigi iyin;
t"1(2x - 5) = 1
olduguna gore, x ka(:t1r?
g(x)
= (2X -
1
x + 1
x>
1
x::; 1
olduguna gre, (go1)(2) + (t"10g)(-2) toplaml ka(:tlr?
Grafigi verilen fonksiyonlar iyin;
(fogof)(1) ifadesinin degeri ka(:t1r?
A)3
8)2
C)1
0)-1
7.
10.
Grafigi verilen
y
y = f(x) fonksiyonu
i~in
r1(3) = -2 + f(x -1)
x
olduguna
kac;t1r?
gore, x
1
y=f(x)
A)-2
B) -1
C)O
0) 1
E) 2
1
Yukarldakl fekle gore, f- (_1) + f- (-2)
nin sonucu kac;tlr?
(t-10r1 )(-4)
1,leml-
E) - .1.
3
Verllenlere gore, (fof)(2x - 4) = 3
saglayan x kac;tlr?
B)
denklemlnl
g(x)
_.1.
0).1.
2
2
Yukanda verilen f(x) ve g(x) fonksiyonlan ic;in;
(fog)(x + 1)
=3
denkleminl saglayan x degerl kac;tlr?
1.
f: A = {D, 1, 2} ~
B,
f(x) = 3x - 2
olduguna gore, f(A) kOmesi al?agldakllerden
hanglsldlr?
A) {-2, 1,5}
B){-2,D,4}
C) {-2, 1,6}
D){-2,1,4}
E){-1,1,4}
f(x) = 2x - 5
x-3
fonkslyonu (1 • 1) ve orten olduguna gore, a + b
ka~tlr?
f(x) = 2x + a , g(x) = bx + 1
fonksiyonlarl 1~ln (fog)(x) fonkslyonu blrlm
fonkslyon olduguna gore, a.b ka~lr?
2.
f(x+1)+2=2f(1-x)
C)l
2
olduguna gore, f(1) ka~tlr?
f(2x - 1) = x + 1
Grafikleri verilen g(x), f(x) fonksiyonlan
olduguna gore, f(x) nedlr?
A)
x+
1
h(x) = (f + (fog))(x)
B)X-1
C)x+3
2
4
2
D)x+2
i~in,
olduguna gore, h(4) ka~tlr?
E)x+3
2
2
f(x) = x - 1
2
olduguna gore, f(x + 1) In f(x) clnslnden degerl
nedir?
f(ax + b)
=2
olduguna gore, f(-1) + f(O)+ f(1) toplaml ka~tlr?
B) f(x) + 1
2
D) f(x) + 1
2
C) f(x) + 1
2
9.
t(3X
-
1)
= 9x -
2.3x + 2
13.
t(x) = 3x - a. g(2) = 5 va (r10g)-1(2) = 2
t(1 + x) = mx
fonkslyonu 1(:ln f(x) = ,-l(X) olduguna gore, m
a,agldakllerden hanglsldlr?
olduguna gore, a ka(:tlr?
t(x)
t(x) = 2x • (tog)(x) = 8.f(x)
11.
B)3
C)4
r1(2x -
12.
16.
1) = g(x)
11.0
2.C
C)3
B) 4
3.E
4.E
5.8
2)x2 + ax + 3
D)5
olduguna gore, (fog)(2) ka(:tlr?
A)5
= (a -
tonkslyonu dogrusal fonkslyon olduguna gore,
tea) ka(:tlr?
olduguna 96re, g(2) ka(:tlr?
A)2
r1(2a + 2) = 5
olduguna gore, a ka(:tlr?
olduguna gore, f(1) ka(:tlr?
10.
t(3x + 2) = 3x - 5 .
2 -
1
olduguna gore, ,-1(3) ka(:tlr?
D) 2
6.8
t(x) = 2X -
7.8
E) 1
8.C
A)2
24
9.8
10.8
B) 3
11.0
12.C
0)5
C)4
13.8
14.0
15.E
E) 6
16.C I